Interaction of Mobile Dislocation with Additives in Ionic Crystals

Study on the strength of materials has been often conducted with simple ionic crystals so far [1-3]. The reason is that the crystals are readily available and have a slight number of glide systems, comparing with metals. On account of it, the crystals contained additives are excellent, when the mechanical properties of materials are investigated. It is well known that the solution hardening due to the additives are caused by the result that mobile dislocations are obstructed by the point defects around them in the crystal at low temperature. The plasticity of crystal varies with dislocation motions in a microscopic observation and the dislocation-additive ions interaction affects the hardening. Dislocation motion on a slip plane has been extensively studied by many different methods: measurements of yield and proof stress (e.g., [4-8]), micro-hardness tests (e.g., [9,10]), microscopy observations (e.g., [11,12]), measurements of internal friction (e.g., [13,14]), or stress relaxation (e.g., [15,16]), but it is difficult to obtain the results on the movement of the dislocation which glides forward breakingaway from the forest dislocations and the point defects such as additives on the slip plane in bulk. On the other hand, the original strain-rate cycling test combined with ultrasonic oscillations is different from the well-known methods. The original tests would be possible to clear up it. Figure 1 shows the illustration of the original tests. The results on the movement of dislocation breakingaway from impediments such as the additives [17,18] and also the defects due to X-ray irradiation [19,20] with the oscillatory stress has been reported by the strain-rate cycling tests combined with ultrasonic oscillations. Applying ultrasonic oscillatory stress to a plastic deforming crystal, a stress decreases and Δτ appears as illustrated in Figure 1. When the strain-rate cycling between the strain rates was conducted keeping the stress amplitude constant, τv, the stress change due to the strain-rate cycling is Δτ’. The Δτ’/ 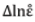has been made an estimate as the strain-rate sensitivity of flow stress, which is termed λ here.

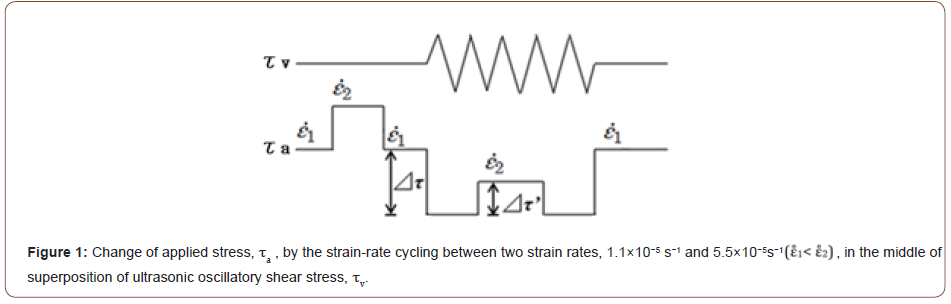
Δτ vs. λ curve looks like a flight of stairs, which has two bending points and two plateau places. Figure 2 shows the Δτ vs. λ curve at 77 to 263 K for NaBr:Li+ (0.5 mol%) [21]. The value of Δτ at first bending point (τ_p denoted in Figure 2) refers to the additive ions in the crystals, since first bending point does not exist on the Δτ vs. λ curves for nominally pure NaBr crystal within the same low temperatures and strains [21]. The value of τ_p tends to be lower at the higher temperature and disappears near atmospheric temperature such as 263 K, as shown in Figure 2. τ_p depends on temperature, also the density and the type of impediments such as point defects [22,23].

The Δτ vs. λ aspect is considered to represent the oscillation effect on the free flight motion of the dislocation on a slip plane during plastic deformation [18]. Additive ions and a few forest dislocations are regarded as main impedimenta to the slip motion of dislocation here. Applying oscillation with high stress amplitude to the crystal, the λ value begins to decrease with increasing Δτ. Some point defects stop acting as obstacles in the region at Δτ beyond τ_p. Second plateau place appears on Δτ vs. λ curve by the oscillation with still higher stress amplitude. At this place, only forest dislocations are expected to act as obstacles to the dislocation slip. Furthermore, the activation energy for the break-away of a dislocation from additive ion has been obtained by analyzing the data on the basis of Δτ vs. λ curve [21].

The original strain-rate cycling tests combined with ultrasonic oscillations clear up the weak point of many different methods. The aspect of the Δτ vs. λ curve obtained from the original method is considered to represent the movement of the dislocation which glides forward breaking-away from the forest dislocations and additive ions on the slip plane in ionic crystal.

None.

No conflict of interest.

1. Kataoka T, Ohji H, Kishida K, Azuma K, Yamada T (1990) Direct Observation of Glide Dislocations in a KCl Crystal by the Light Scattering Method. Appl Phys Lett 56(14): 1317-1319.
2. Sprackling MT (1976) The Plastic Deformation of Simple Ionic Crystals. Academic Press, London.
3. Zakrevskii VA, Shul’diner AV (2000) Dislocation Interaction with Radiation Defects in Alkali-Halide Crystals. Physics of the Solid State 42(2): 270-273.
4. Boyarskaya YS, Zhitaru RP, Palistrant NA (1990) The anomalous behaviour of the doped NaCl crystals compressed at low temperatures. Crystal Research and Technology 25(12): 1469-1473.
5. Okazaki K (1996) Solid-solution hardening and softening in binary iron alloys. Journal of Materials Science 31: 1087-1099.
6. Tabachnikova ED, Podolskiy AV, Smirnov SN, Psaruk IA, Liao PK (2014) Temperature dependent mechanical properties and thermal activation plasticity of nanocrystalline and coarse grained Ni-18.75 at. % Fe alloy. IOP Conference Series: Materials Science and Engineering 63(1): 012105.
7. Pratt PL, Harrison RP, Newey CWA (1964) Dislocation mobility in ionic crystals. Discussions of the Faraday Society 38: 211-217.
8. Newey CWA, Harrison RP, Pratt PL (1966) Precipitation hardening and dislocation locking in doped NaCl. Proceedings of the British Ceramic Society 6: 305-316.
9. Buravleva MG, Rozenberg GK, Soifer LM, Chaikovskii EF (1980) Changes in the flow stress of LiF:Mg²⁺ and LiF:Co²⁺ crystals during precipitation of solid solutions. Soviet Physics. Solid State 22: 150-152.
10. Narasimha Reddy K, Subba Rao UV (1984) Influence of gadolinium impurity on microhardness of host alkali halide crystal. Crystal Research and Technology 19(7): K73-K76.
11. Kataoka T, Ohji H, Kishida K, Azuma K, Yamada T (1990) Direct observation of glide dislocations in a KCl crystal by the light scattering method. Applied Physics Letters 56(14): 1317-1319.
12. Messerschmidt U (2010) Dislocation Dynamics During Plastic Deformation. Berlin Heidelberg: Springer.
13. Kosugi T (2001) Temperature dependence of amplitudedependent internal friction due to simultaneous breakaway of a dislocation from several pinning points. Materials Science and Engineering A 309-310: 203-206.
14. Gremaud G (2001) Dislocation-point defect interactions. Materials Science Forum 366-368: 178-246.
15. Dotsenko VI (1979) Stress relaxation in crystals. Physica Status Solidi (b) 93(1): 11-43.
16. Urusovskaya AA, Petchenko AM, Mozgovoi VI (1991) The influence of strain rate on stress relaxation. Physica Status Solidi (a) 125(1): 155-160.
17. Kohzuki Y (2009) Study on the interaction between a dislocation and impurities in KCl:Sr²⁺ single crystals by the Blaha effect-Part IV influence of heat treatment on dislocation density. Journal of Materials Science 44: 379-384.
18. Kohzuki Y (2010) Bending angle of dislocation pinned by an obstacle and the Friedel relation. Philosophical Magazine 90(16): 2273-2287.
19. Ohgaku T, Migiuma S, Nagahira D (2011) Interaction between dislocation and defects induced by X-irradiation in alkali halide crystals. Radiation Measurements 46: 1385-1388.
20. Kohzuki Y, Ohgaku T (2017) X-ray-induced defects as obstacles to dislocation motion in alkali halide crystals. Journal of Materials Science 52(7): 3959–3966.
21. Kohzuki Y, Ohgaku T (2017) Study on influence of additive and host ions on deformation characteristics of alkali halide crystals by strainrate cycling tests during the Blaha effect. Crystal Research and Technology 52(3): 1600290.
22. Ohgaku T, Teraji H (2001) Investigation of interaction between a dislocation and a Br⁻ ion in NaCl:Br⁻ single crystals. Physica Status Solidi (a) 187(2): 407-413.
23. Ohgaku T, Matsunaga T (2009) Interaction between dislocation and divalent impurity in KBr single crystals. IOP Conference Series: Materials Science and Engineering 3: 012021.