Hall Effect Phenomena

The anomalous Hall Effect phenomenon has a long history behind it which is connected to the history of magnetism and electricity. In 1879 Erwin H. Hall, made a historic discovery [1] at the University of Baltimore, that when a conductor or semiconductor with current flowing in one direction was introduced to a perpendicular magnetic field H, a voltage could be measured at right angles to the current path. Later in 1881 he reported that this effect was ten times larger in ferromagnetic iron [2]. It is remarkable, though, that the first Hall discovery was made almost three decades prior to the electron discovery by J.J. Thomson in 1897. Since the transverse resistance (or Hall resistance), defined as UH/I, is proportional to H/n, where n is the sheet carrier density of the sample, the Hall effect provides a simple sophisticated method, that has been extensively used, to compute the carrier type (electron or hole), density, and the mobility of materials. The ability to calculate the carrier concentration in nonmagnetic conductors and semiconductors has played a critical role for the birth of semiconductor physics and solid state electronics. The second Hall discovery in ferromagnetic conductors is known as the anomalous Hall Effect (AHE) (Figure 1).

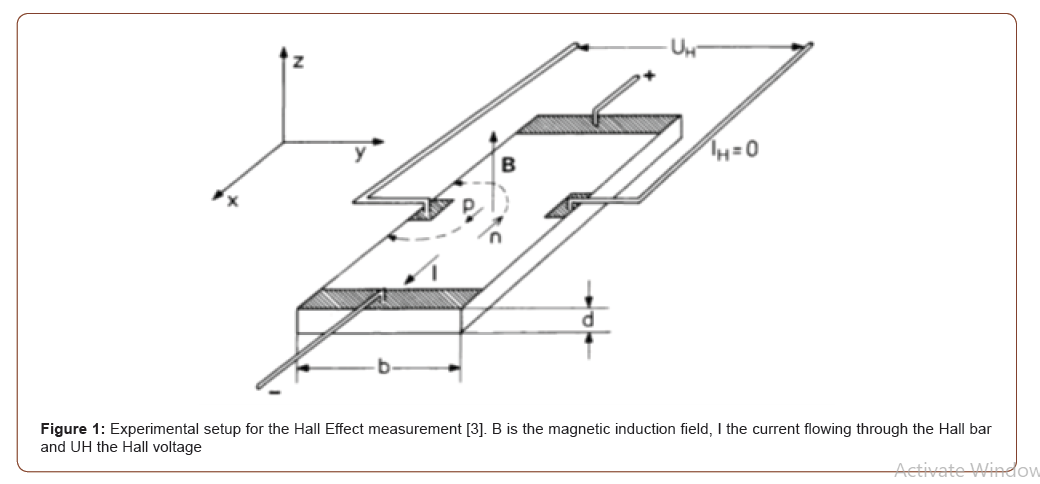
In ferromagnetic materials the resistivity of the sample in the direction that is perpendicular to external electric E and magnetic H field acquires an additional contribution due to the magnetization of the sample [4,5]:

where R0 is the Hall coefficient, Rs is the anomalous Hall coefficient, ρ_OH is the ordinary Hall resistivity and ρ_AH is the anomalous Hall resistivity.

The AHE is used today for the purposes of modern spintronics and is a unique tool for generating and controlling spin-polarized currents in complex magnetic nanoscale systems. The understanding of the mechanisms of the AHE is necessary for further developments in the field of spin Hall Effect and the related phenomena, which are based on propagation of pure spin currents without accompanying charge transport (Figure 2).

The recent progress in understanding the AHE from the approach of Berry phases and the topological structure of the electronic bands led to the point that many abstract quantities and objects in this part of quantum physics became measurable and achievable to explore experimentally.

Figure 2 clarifies the two main extrinsic contributions to AHE and spin Hall Effect (SHE) that are described below, specifically, skew scattering (a) and side-jump scattering (b). Both are caused by spin–orbit coupling (SOC), that is, the electron partially orbits around an impurity atom and thereby creates a small orbital moment, which depends on the spin through SOC. The impurity is not certainly magnetic, but a magnetization is mandatory to create a net voltage. (No net magnetic moment is essential for the SHE). The skew scattering changes the direction of the electron velocity v, creating a perpendicular component Δv and a net electron displacement T_RΔv, where T_R =l/v is the relaxation time.

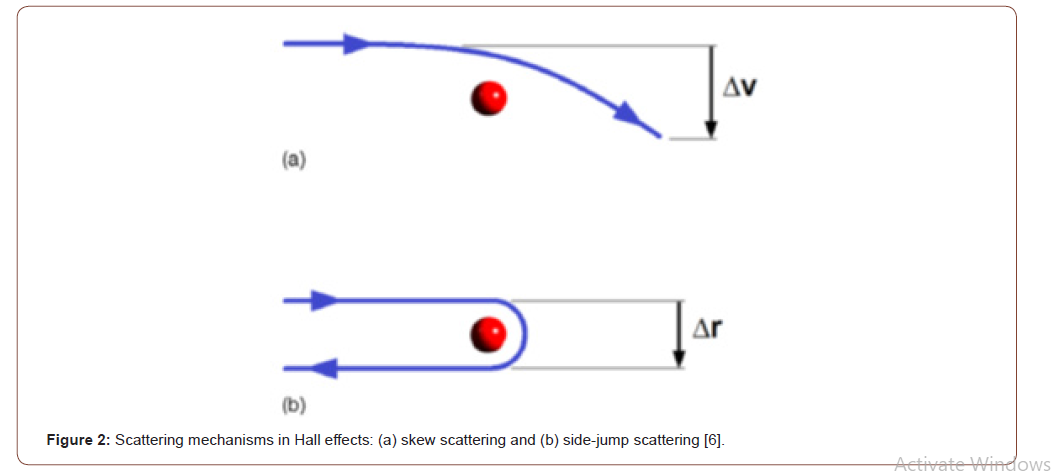
Side-jump scattering does not amount to a perpendicular velocity component (Δv=0) but a finite displacement Δr.

Skew scattering is linear in the resistivity ρxx and dominates in rather pure metals, whereas side-jump scattering scales as ρ2 xx, and dominates in reasonably disordered metals. There is also an intrinsic (resistivity-independent) Hall contribution due to the Berry phase. This contribution influences the periodic electronic structure of the material.

In the 1980s it was found that when the charge carriers are confined to a two-dimensional (2D) film, the Hall resistance becomes quantized at h/(ve2), where h is the Planck constant, e is the electron charge, and v is a positive integer and H/n approaches precise values. This phenomenon was named the quantum Hall effect (QHE) [7] and the presence of an external magnetic field is necessary for its observation.

The spin Hall effect (SHE) predicted by Russian physicists Mikhail I. Dyakonov and Vladimir I. Perel in 1971 [8] involves the presence of spin accumulation on the edge of the surfaces of a sample carrying electric current. The opposite surface boundaries will have spins of opposite sign and thus it is equivalent to the classical Hall Effect. No magnetic field is needed for the SHE which is a purely spin-based phenomenon. Experimentally it was realized about 30 years later [9] in unstrained gallium arsenide and strained indium gallium arsenide semiconductors. The SHE belongs to the same family as the anomalous Hall Effect, that was already known in ferromagnetic materials and both originate from the spin-orbit interaction.

The quantum spin Hall (QSH) state is a state of matter proposed to exist in special, two-dimensional, semiconductors that have a quantized spin-Hall conductance and a vanishing charge-Hall conductance. In 1988, it was proposed that the existence of the QSH state shown theoretically in such an edge channel can exist on a two-dimensional lattice [10]. Then, almost 20 years later, the experimental demonstration of the presence of lossless edge channels in a HgTe/CdTe quantum well, which exhibits an integer quantum Hall effect in the absence of an external magnetic field, was reported [11] (Figure 3).

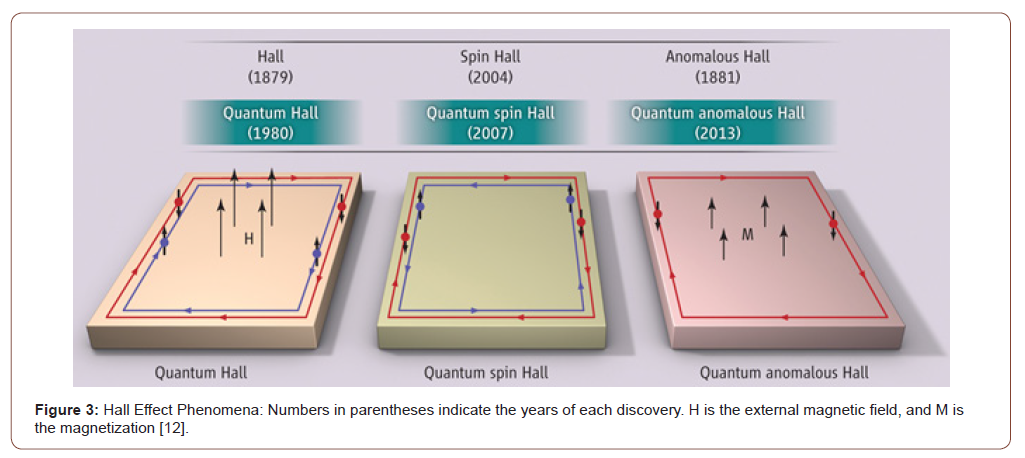
If one of the spin channels in the QSH effect system is silenced - by introducing ferromagnetism - it logically leads to the quantum anomalous Hall Effect (QAHE) which is a quantized version of the above mentioned AHE. It was later predicted that for a magnetically doped topological insulator Bi₂Se₃sub> thin film, the system should exhibit the QAHE with a quantized Hall resistance of h/e₂ [13].

Topological Insulators (TIs) [14] are materials that are electrical insulators in the bulk, but can conduct electricity on their surface via special surface electronic states. They offer the chance to enlarge our understanding of materials physics and could lead to applications such as quantum computation.

The surface of a TI hosts symmetry-protected gapless Dirac electrons with spin direction locked perpendicular to their momenta. When doped with magnetic elements such as Cr, Mn etc, TIs can host a large variety of magnetic phases, such as ferromagnetic, paramagnetic, noncolinear, and spin glass phases, due to various types of exchange interactions between the magnetic impurities in presence of the surface and bulk states. The magnetically doped TIs have received intensive experimental attention, and the work on ferromagnetic (FM) order in Cr-doped (Bi,Sb)2Te3 thin films has led to the discovery of quantum anomalous Hall effect (QAHE) [15].

This work was financially supported by the Air Force Office of Scientific Research (AFOSR) under award number FA9550-17-1- 0178.

No conflict of interest.

1. Hall EH (1879) On a New Action of the Magnet on Electric Currents. Am J Math 2(3): 287-292.
2. Hall EH (1881) On the new action of magnetism on a permanent electric current. Philos Mag 10(63): 301-328.
3. Harald Ibach, Hans Lueth (2009) Solid-State Physics. Condensed Matter Physics, Springer.
4. CM Hurd (1972) The Hall Effect in Metals and Alloys. Plenum, New York.
5. CL Chien, CR Westgate (1980) The Hall Effect and Its Applications. Plenum, New York.
6. Yanglong Hou, David J Sellmyer (2017) Magnetic Nanomaterials, Willey, pp. 67.
7. Klitzing KV, Dorda G, Pepper M (1980) New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys Rev Lett. 45(6): 494-497.
8. Dyakonov MI, Perel VI (1971) Possibility of orientating electron spins with current. Sov Phys JETP Lett 13: 467.
9. YK Kato, RC Myers, AC Gossard, DD Awschalom (2004) Observation of the Spin Hall Effect in Semiconductors. Science 306( 5703): 1910-1903.
10. Haldane FDM (1988) Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the "Parity Anomaly”. Physical Review Letters 61(18): 2015-2018.
11. Markus König, Steffen Wiedmann, Christoph Brüne, Andreas Roth, Hartmut Buhmann, et al. (2007) Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 318(5851): 766-770.
12. Seongshik Oh (2013) The Complete Quantum Hall Trio. Science 340(6129): 153-154.
13. Rui Yu, Wei Zhang, Hai-Jun Zhang, Shou-Cheng Zhang, Xi Dai, et al. (2010) Quantized Anomalous Hall Effect in Magnetic Topological Insulators. Science 329(5987): 61-64.
14. Joel E Moore (2010) The birth of topological insulators. Nature 464(7286): 194-198.
15. Nan Liu, Jing Teng, Yongqing Li (2018) Two-component anomalous Hall effect in a magnetically doped topological insulator. Nature Communications 9 Article number: 1282.