 Review Article
Review Article
Exciton Quasimolecules and Exciton Quasicrystals: Theory
Sergey I Pokutnyi*
Department of Theoretical Physics of Nano systems, Chuіko Institute of Surface Chemistry of National Academy of Sciences of Ukraine, Ukraine
Sergey I Pokutnyi, Department of Theoretical Physics of Nano systems, Chuіko Institute of Surface Chemistry of National Academy of Sciences of Ukraine, Kyiv 03164, Ukraine.
Received Date: November 13, 2019 Published Date: December 02, 2019
Abstract
In review, deals with the theory of exciton Quasimolecules in a Nano heterostructures. It has been found that the formation of a exciton Quasimolecules in a Nano heterostructures made up of aluminum oxide quantum dots synthesized in a dielectric matrix is of threshold character and can occur in a Nano systems where the distance D between the surfaces of quantum dots is given by the condition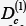 The existence
of such distance
The existence
of such distance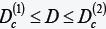 arises from quantum size effects in which the decrease in the energies of interaction of the electrons and holes entering into the Hamiltonian of the “exciton molecule” with decrease of the distance D between the surfaces of the QD cannot compensate for the increase in the kinetic energy of the electrons and holes. At larger distances D between the surfaces of quantum dots:
arises from quantum size effects in which the decrease in the energies of interaction of the electrons and holes entering into the Hamiltonian of the “exciton molecule” with decrease of the distance D between the surfaces of the QD cannot compensate for the increase in the kinetic energy of the electrons and holes. At larger distances D between the surfaces of quantum dots: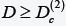 the biexciton breaks down into two
excitons (consisting of spatially separated electrons and holes), localized over QD surfaces.
the biexciton breaks down into two
excitons (consisting of spatially separated electrons and holes), localized over QD surfaces.
It was shown that the convergence of two quantum dots up to a certain critical value
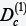 between surfaces of quantum dot lead to overlapping
of electron orbitals of super atoms and the emergence of exchange interactions. In this case the overlap integral of the electron wave functions takes
a significant value. As a result, the conditions for the formation of quasi-molecules from quantum dots can be created.
between surfaces of quantum dot lead to overlapping
of electron orbitals of super atoms and the emergence of exchange interactions. In this case the overlap integral of the electron wave functions takes
a significant value. As a result, the conditions for the formation of quasi-molecules from quantum dots can be created.
We have shown that in such a Nano heterostructures acting as “exciton molecules” (biexcitons consisting of spatially separated electrons and holes) are the quantum dots of aluminum oxide with excitons localizing over their surfaces. The position of the biexciton state energy band depends both on the mean radius of the quantum dots, and the distance between their surfaces, which enables one to purposefully control it by varying these parameters of the nanostructure.
As our variational calculations show, the interaction of the excitons with the surfaces of quantum dots (“intramolecular” interaction) is much stronger than that between quantum dots (“intermolecular” interaction). Due to the translational symmetry of such a Nano heterostructures of quantum dots, it permits propagation of electronic excitation in the form of biexcitons.
As follows form the results of the variational calculations, the major contribution to the biexciton binding energy is from the energy of exchange interaction of electrons and holes, which by far surpasses that from their Coulomb interaction.
It is established that at constant concentrations of biexcitons at temperatures T below a certain critical temperature Tc due to the radiative
annihilation of one of the excitons forming a biexciton one can expect a new spectral band of luminescence shifted relative to the exciton band by the
biexciton binding energy Eв. This new luminescence band disappears at temperatures above Tc. At a constant temperature Т Keywords: Electrons; Holes; Biexciton ground singlet states; Binding energy; Coulomb; Polarization and exchange interaction; Quantum dots;
Nano heterostructures
Introduction
Recent advances of solid-state technology made it possible to produce a nano heterostructures (NHS), where acting as lattice points are spherical dielectric or semiconductor quantum dots (QDs) with the mean radius a =1-10 nm implanted in a transparent dielectric (or semiconductor) matrix [1]. Such sizes of QD are comparable with the de Broglie wavelength of the electron and hole or (and) with their Bohr radii. This leads to the spatial dimensional quantization of charge carriers playing a substantial part in optical and electro-optical processes in such nano systems [1-24].
The studies of quasi 0-sD nano systems made up of spherical QD with the mean radius in the range of 1 to 10 nm consisting of semiconductor (cadmium sulfide and selenide, gallium arsenide, zinc selenide) [1-3] and dielectric (aluminum oxide) [4-6] materials synthesized in dielectric (semiconductor) matrices attract considerable interest due to their unique photoluminescence properties, ability to effectively emit light in the visible and near infrared spectral range at room temperatures [1-6]. Optical and electro-optical properties of such quasi 0-D nano systems are to a large extent governed by the energy spectrum of the spatially confined electron-hole pair (exciton) [1-24].
During investigation of the optical characteristics of nano systems with CdS, ZnSe, Al2O3 and Ge quantum dots in experimental papers [11-15] it was found that the electron can be localized above the surface of the QD while the hole here moves in the volume of the QD. In [25-29] the appearance of super atoms located in dielectric matrices as cores containing CdS, ZnSe, Al2O3 and Ge quantum dots was apparently established experimentally for the first time. A substantial increase in the bond energy of the ground state of an electron in a super atom in comparison with the bond energy of an exciton in CdS, ZnSe and Al2O3 and single crystals was detected in [8].
In [26-29] the optical characteristics of samples of borosilicate glasses doped with CdS, ZnSe and Al2O3 at concentrations between x≈0.003% to 1% were investigated. The average radii ā of CdS and ZnSe QDs were in the range of ā≈2.0-20 nm. When there were large concentrations of CdS quantum dots in the samples (from x≈0.6% to x≈1%) a maximum, interpreted by the appearance of bonded QD states, was detected in the low-temperature absorption spectra. In order to explain the optical characteristics of such nano systems we proposed a model of a quasimolecule representing two ZnSe and CdS QDs that form an exciton quasimolecule as a result of the interaction of electrons and holes.
It was noted [25,27] that, at such a QD content in the samples, one must consider the interaction between charge carriers localized above the QD surfaces. Therefore, in [10,15], we develop the theory of an exciton quasimolecule (or biexciton) (formed from spatially separated electrons and holes) in a nano system that consists of ZnSe and CdS QDs synthesized in a borosilicate glassy matrix. Using the variational method, we obtain the total energy and the binding energy of the exciton quasimolecule (or biexciton) singlet ground state in such system as functions of the spacing between the QD surfaces and of the QD radius. We show that the biexciton formation is of the threshold character and possible in a nano system, in which the spacing between the QD surfaces exceeds a certain critical spacing. It is established that the spectral shift of the low-temperature luminescence peak [27] in such a nano system is due to quantum confinement of the energy of the biexciton ground state.
The convergence of two (or more) QDs up to a certain critical value Dc between surfaces of QD lead to overlapping of electron orbitals of super atoms and the emergence of exchange interactions [9]. In this case the overlap integral of the electron wave functions takes a significant value. As a result, the conditions for the formation of quasi-molecules from QDs can be created [10]. One can also assume that the above conditions of formation of quasimolecules can be provided by external physical fields. This assumption is evidenced by results of [30,31], in which the occurrence of the effective interaction between QDs at considerable distances under conditions of electromagnetic field was observed experimentally. In [32] energies of the ground state of “vertical” and “horizontal” located pair of interacting QDs (“molecules” from two QDs) were determined as a function of the steepness of the confining potential and the magnetic field strength. The quantum part of nano computer, which was implemented on a pair of QDs (“molecules” from two QDs) with charge states is n qubits [33]. The first smoothly working quantum computer has been on QDs with two electron orbital states as qubits, described by a pseudospin (½). As a single cell was taken a couple of asymmetric pair QDs with different sizes and significantly different own energy. The electron injected into the heterostructure from the channel occupied the lower level. That is, it was in a QD with larger size.
In the present review we show that the biexciton formation in
a NHS made up of aluminum oxide quantum dots synthesized in a
dielectric matrix is of threshold character and can occur in a nano
system where the distance D between the surfaces of QD is given
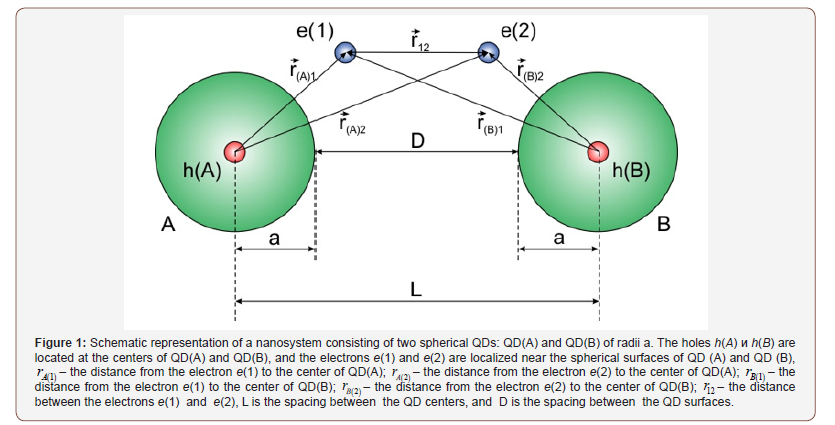
by the condition Let us consider a model of a nano system composed of two
dielectric (semiconductor) spherical quantum dots QD(A) and
QD(B) of radius а synthesized in a dielectric matrix with permittivity
ε1 (D is the distance between the spherical surfaces of QD). Quantum
dots are of a dielectric (semiconductor) material with permittivity
ε2. For simplicity and without loss of generality let us assume that
holes h(A) и h(B) with effective masses mh are located at the centers of QD (A) and QD (B) while electrons е(1) and е(2) with effective masses Let us now use this model to consider the possibility of the
formation of an exciton from spatially separated electrons and
holes (the holes are located at the centers of QD(A) and QD(B)
and electrons are localized near their spherical surfaces). Using
adiabatic approximation and the effective mass approximation, the
Hamiltonian of the biexciton (of spatially separated electrons and
holes) can be written in the form [15]: where where the first term is the exciton kinetic energy operator and
the energy of Coulomb interaction where Eg is the bandgap energy of the dielectric (semiconductor)
with permittivity ε2.The Hamiltonian Under the assumption that the spins of the electrons е(1) and
е(2) are antiparallel let us write down the normalized wave function
of the ground singlet state of the biexciton as a symmetric linear
combination of wave functions where S (D, a) is the overlap integral of single-electron wave
functions. Assuming that the electrons e(1) and e(2) move
independently from each other, let us represent the wave functions
where is the Bohr radius of the 2D exciton localized over the flat interface
between the semiconductor (dielectric) with permittivity ε2 and the
matrix with permittivity ε1 (the hole is in the semiconductor and
the electron is in the matrix, е is the electron charge, In the framework of the variational method, the energy of the
biexciton ground singlet state, as a first approximation, is given by
the mean value of the Hamiltonian H (1) over the states described
by the wave functions of the 0th approximation Ψs (4) [15]: As follows from (6), the total energy 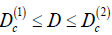 We also demonstrate that in such
NHS acting as “exciton molecules” (or biexciton) are the quantum
dots of aluminum oxide with excitons localizing over their surfaces.
The position of the biexciton state energy band is shown to depend
both on the mean radius of quantum dots, and the distance
between their surfaces, which enables one to purposefully control
it by varying these parameters of the NHS. It is established that
at constant concentrations of biexcitons at temperatures T below
a certain critical temperature Tc due to the radiative annihilation
of one of the excitons forming a biexciton one can expect a new
spectral band of luminescence shifted relative to the exciton band
by the biexciton binding energyEa. This new luminescence band
disappears at temperatures above Tc. At a constant temperature
Т
We also demonstrate that in such
NHS acting as “exciton molecules” (or biexciton) are the quantum
dots of aluminum oxide with excitons localizing over their surfaces.
The position of the biexciton state energy band is shown to depend
both on the mean radius of quantum dots, and the distance
between their surfaces, which enables one to purposefully control
it by varying these parameters of the NHS. It is established that
at constant concentrations of biexcitons at temperatures T below
a certain critical temperature Tc due to the radiative annihilation
of one of the excitons forming a biexciton one can expect a new
spectral band of luminescence shifted relative to the exciton band
by the biexciton binding energyEa. This new luminescence band
disappears at temperatures above Tc. At a constant temperature
ТEnergy of the Exciton Quasimolecules Ground
Singlet State Formed from Spatially Separated
Electrons and Holes
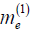 are localized near the spherical surfaces of QD (A) and QD (B), respectively
are localized near the spherical surfaces of QD (A) and QD (B), respectively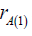 the distance from the electron е(1) to the
center of QD (A);
the distance from the electron е(1) to the
center of QD (A);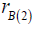 the distance from the electron е(2) to the
center of QD (B) (Figure 1). This assumption is justified by the fact
that
the distance from the electron е(2) to the
center of QD (B) (Figure 1). This assumption is justified by the fact
that 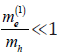 Let us also infer that an infinitely high potential barrier exists on the spherical interface between the QD and the matrix so
that the electrons cannot get into the quantum dot while the holes
cannot escape from it.
Let us also infer that an infinitely high potential barrier exists on the spherical interface between the QD and the matrix so
that the electrons cannot get into the quantum dot while the holes
cannot escape from it.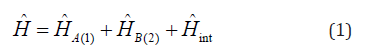
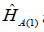 and
and
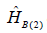 are the Hamiltonians of the excitons
of spatially separated hole h(A) and electron е(1) and hole h(B)
and electron е(2), respectively. The contribution of the energy of
polarization interaction with the surface of QD to the Hamiltonians
of the excitons
are the Hamiltonians of the excitons
of spatially separated hole h(A) and electron е(1) and hole h(B)
and electron е(2), respectively. The contribution of the energy of
polarization interaction with the surface of QD to the Hamiltonians
of the excitons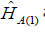 and
and
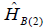 can be, as a first approximation
neglected [20]. Thus, the exciton Hamiltonian
can be, as a first approximation
neglected [20]. Thus, the exciton Hamiltonian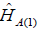 takes the form
[15]:
takes the form
[15]: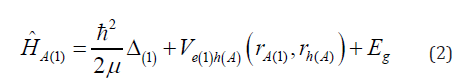
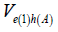 between electron е(1)
and hole h(A) is given be the following expression [7,8]:
between electron е(1)
and hole h(A) is given be the following expression [7,8]: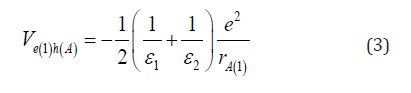
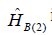 is of the same form as
is of the same form as
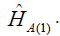 In the first approximation we can neglect the contributions to the Hamiltonian H ̂int of the interaction energies of the electrons
e(1) and e(2) and the holes h(A) and h(B) with polarization fields
induced by these charge carriers on the surfaces of QD (A) and QD
(B) [20]. Thus the Hamiltonian
In the first approximation we can neglect the contributions to the Hamiltonian H ̂int of the interaction energies of the electrons
e(1) and e(2) and the holes h(A) and h(B) with polarization fields
induced by these charge carriers on the surfaces of QD (A) and QD
(B) [20]. Thus the Hamiltonian 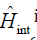 incorporates only the energies
of Coulomb interaction of electron e(1) with hole h(B), and electron
е(2) with hole h(A), as well as that between electrons е(1) and е(2),
and holes h(A) and h(B).
incorporates only the energies
of Coulomb interaction of electron e(1) with hole h(B), and electron
е(2) with hole h(A), as well as that between electrons е(1) and е(2),
and holes h(A) and h(B).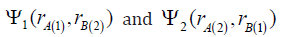 [15]:
[15]: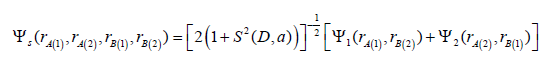
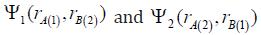 as a product of single-electron
wave functions
as a product of single-electron
wave functions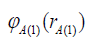 as well as
as well as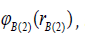 and
and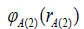 respectively [15]. Let us also represent the singleelectron wave functions as variational functions of Coulomb type
[15]:
respectively [15]. Let us also represent the singleelectron wave functions as variational functions of Coulomb type
[15]: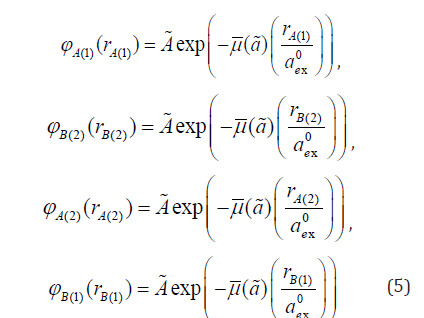
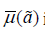 is a variational parameter,
is a variational parameter,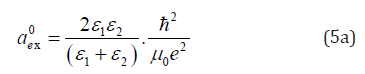
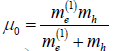 is the reduced effective mass of the 2D exciton,
is the reduced effective mass of the 2D exciton,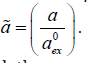
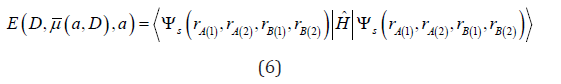
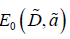

where 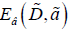 is the binding energy of the ground singlet state
of the biexciton, and
is the binding energy of the ground singlet state
of the biexciton, and 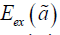 is the binding energy of the ground
state of the exciton (consisting of spatially separated electron and
hole) localized over the surface of QD, which was worked out in
[7,8] (Figure 2)
is the binding energy of the ground
state of the exciton (consisting of spatially separated electron and
hole) localized over the surface of QD, which was worked out in
[7,8] (Figure 2)
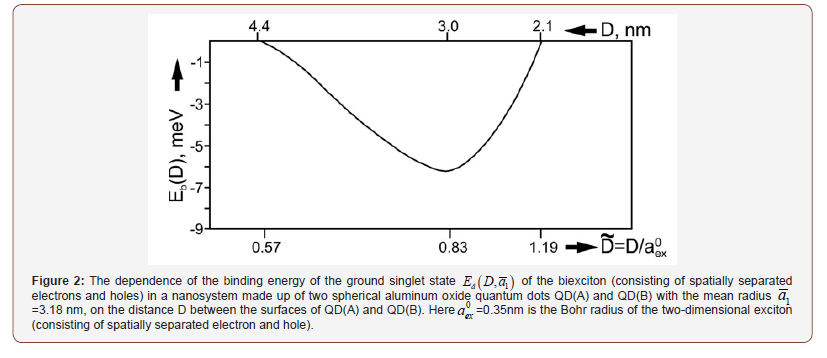
Figure 2 presents the results of the variational calculations
of the binding energy 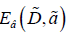 studied in [4-6] of the biexciton
ground state in a nano system with QD of aluminum oxide of the
mean radius
studied in [4-6] of the biexciton
ground state in a nano system with QD of aluminum oxide of the
mean radius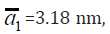 (permittivity ε2 = 10 , effective mass of
the hole in QD synthesized in a dielectric matrix of the
vacuum oil VM-4 (permittivity ε1 = 1.96, the effective mass of the
electron in the matrix
(permittivity ε2 = 10 , effective mass of
the hole in QD synthesized in a dielectric matrix of the
vacuum oil VM-4 (permittivity ε1 = 1.96, the effective mass of the
electron in the matrix 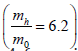 was deduced in [21] and amounts to 0,537, the Bohr radius (5а) of the 2D exciton
was deduced in [21] and amounts to 0,537, the Bohr radius (5а) of the 2D exciton 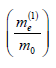 Authors of [4-6] studied nanostructures doped with х = 0.003% to 1% concentrations of aluminum oxide. At concentrations of
QD higher than x ≅ 0.6% one needs to consider the interactions
of the charges localized over the surfaces of quantum dots. The
variational method that we used for the calculation of the biexciton
ground state binding energy
Authors of [4-6] studied nanostructures doped with х = 0.003% to 1% concentrations of aluminum oxide. At concentrations of
QD higher than x ≅ 0.6% one needs to consider the interactions
of the charges localized over the surfaces of quantum dots. The
variational method that we used for the calculation of the biexciton
ground state binding energy 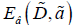 is applicable provided that it
is much smaller than the binding energy of the exciton ground state
is applicable provided that it
is much smaller than the binding energy of the exciton ground state
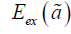 i.e. the following condition must be fulfilled:
i.e. the following condition must be fulfilled:

The binding energy 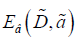 of the biexciton ground state in
a nano system with QD of aluminum oxide of the mean radius
of the biexciton ground state in
a nano system with QD of aluminum oxide of the mean radius 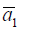 =3.18 nm has a minimum
=3.18 nm has a minimum 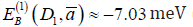 (at the distance
D1≅2.93 nm) (Figure 2)
(at the distance
D1≅2.93 nm) (Figure 2) corresponds to the critical temperature
Tс ≈ 81.6 K). As it follows form Figure 1, biexciton appears in the
nano system at distances
corresponds to the critical temperature
Tс ≈ 81.6 K). As it follows form Figure 1, biexciton appears in the
nano system at distances 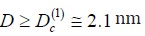 between the surfaces
of QD. The formation of such a biexciton (,,exciton molecule”) is of
threshold character and can occur in a nano system with quantum
dots of the mean radius a ̅1, where the distance D between the
surfaces of QD exceeds a certain critical value (1)
. The existenceof such distance
between the surfaces
of QD. The formation of such a biexciton (,,exciton molecule”) is of
threshold character and can occur in a nano system with quantum
dots of the mean radius a ̅1, where the distance D between the
surfaces of QD exceeds a certain critical value (1)
. The existenceof such distance 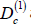 arises from quantum size effects in which the
decrease in the energies of interaction of the electrons and holes
entering into the Hamiltonian (Eq. (1)) of the “exciton molecule”
with decrease of the distance D between the surfaces of the QD
cannot compensate for the increase in the kinetic energy of the
electrons and holes.
arises from quantum size effects in which the
decrease in the energies of interaction of the electrons and holes
entering into the Hamiltonian (Eq. (1)) of the “exciton molecule”
with decrease of the distance D between the surfaces of the QD
cannot compensate for the increase in the kinetic energy of the
electrons and holes.
The binding energy of the exciton 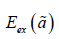 amounts to
amounts to
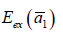 ≅-100.8 meV [7,8], with the energy of the biexciton ground state (7) taking the value
≅-100.8 meV [7,8], with the energy of the biexciton ground state (7) taking the value 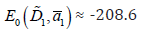 meV. It should be emphasized
that the criterion (8) of the applicability of the variational method for
the calculation of the biexciton binding energy
meV. It should be emphasized
that the criterion (8) of the applicability of the variational method for
the calculation of the biexciton binding energy 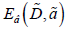 is fulfilled
is fulfilled
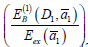 ≅0.07. At larger distances D between the surfaces of
≅0.07. At larger distances D between the surfaces of 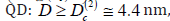 the biexciton breaks down into two excitons
(consisting of spatially separated electrons and holes), localized
over QD surfaces (Figure 1). Thus, a biexciton can be formed in a
nano system where
the biexciton breaks down into two excitons
(consisting of spatially separated electrons and holes), localized
over QD surfaces (Figure 1). Thus, a biexciton can be formed in a
nano system where 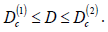 Furthermore, a biexciton can
exist only at temperatures lower than the critical temperature Tc =
81.6 K. In the aluminum oxide monocrystal with the binding energy
Furthermore, a biexciton can
exist only at temperatures lower than the critical temperature Tc =
81.6 K. In the aluminum oxide monocrystal with the binding energy 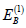 is almost 12 times as large.
is almost 12 times as large.
As follows form the results of the variational calculations, the
major contribution to the biexciton binding energy is from the
energy of exchange interaction of electrons and holes, which by
far surpasses that from their Coulomb interaction (i.e. the ratio ≤
0.11). Since the calculations of the biexciton ground state binding energy 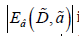 in the nano system are variational, the values of
in the nano system are variational, the values of
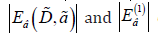 can be somewhat underestimated.
can be somewhat underestimated.
Biexciton in Quasicrystal
In a NHS (mean radius of QD 1 a = 3.18 nm, and the distance between the surfaces of aluminum oxide QD D1 = 2.93 nm) at temperatures below the critical value Tc = 81.6K (which corresponds to the biexciton binding energy Eâ = 7.03 meV) an “exciton molecule” can be formed (biexciton consisting of spatially separated electrons and holes). Acting as “exciton molecules” in such an NHS are the quantum dots of aluminum oxide, with excitons (consisting of spatially separated electrons and holes) localized over their surfaces. As our variational calculations show, the interaction of the excitons with the surfaces of QD (“intramolecular” interaction) is much stronger than that between quantum dots (“intermolecular” interaction). Due to the translational symmetry of such an NHS of QD, it permits propagation of electronic excitation in the form of biexcitons.
The energy level of the biexciton 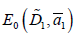 (7) turns, in this case,
into a biexciton energy band with the width
(7) turns, in this case,
into a biexciton energy band with the width 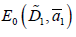 (where
(where 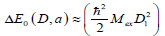 is the translational mass of the exciton
of spatially separated electron and hole). Quantitative assessment
of the width of the biexciton band yields the value of about 3 meV
(which corresponds to the temperature of 35 K). In such an NHS
the energy band of biexciton states is located below the bandgap
of aluminum oxide NHS by
is the translational mass of the exciton
of spatially separated electron and hole). Quantitative assessment
of the width of the biexciton band yields the value of about 3 meV
(which corresponds to the temperature of 35 K). In such an NHS
the energy band of biexciton states is located below the bandgap
of aluminum oxide NHS by 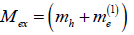 is the translational mass of the exciton
of spatially separated electron and hole). Quantitative assessment
of the width of the biexciton band yields the value of about 3 meV
(which corresponds to the temperature of 35 K). In such an NHS
the energy band of biexciton states is located below the bandgap
of aluminum oxide NHS by
is the translational mass of the exciton
of spatially separated electron and hole). Quantitative assessment
of the width of the biexciton band yields the value of about 3 meV
(which corresponds to the temperature of 35 K). In such an NHS
the energy band of biexciton states is located below the bandgap
of aluminum oxide NHS by 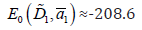 The position
of this energy band is governed both by the mean radius
The position
of this energy band is governed both by the mean radius 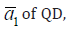 and the distance D1 between QD surfaces. Thus, by varying these
parameters of the NHS, one can purposefully control the position of
the energy band of biexciton states.
and the distance D1 between QD surfaces. Thus, by varying these
parameters of the NHS, one can purposefully control the position of
the energy band of biexciton states.
At higher temperatures (Т ≥ Tc), a phase transition of the nano system can occur from the biexciton to exciton state. At a constant concentration of excitons (i.e. constant concentration of QD) and temperatures Т lower than Tc, one can expect a new luminescence band shifted from the exciton band by the value of the biexciton binding energy â E . This new band disappears at higher temperatures (Т ≥ Tc). At a constant temperature below critical (Т< Tc), an increase in exciton concentration (i.e. in QD concentration) brings about weakening of the exciton luminescence band and strengthening of the biexciton one.
Conclusion
Thus it has been shown that the exciton quasimolecule
formation in a NHS made up of aluminum oxide quantum dots (QD)
of the mean radius 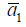 is of threshold character and can occur in
a nano system where the distance D between the surfaces of QD
is given by the condition
is of threshold character and can occur in
a nano system where the distance D between the surfaces of QD
is given by the condition 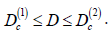 have demonstrated
that in such a NHS (with the mean radius 1 a = 3.18 nm and the
distance between surfaces of aluminum oxide QD D1 = 2.93 nm)
at temperatures lower than the critical temperature Tc = 81.6K
(which corresponds to the exciton quasimolecule binding energy
â E = 7.03 meV) an ,,exciton molecule“ (a biexciton consisting of
spatially separated electrons and holes) can be formed. Acting
as “exciton molecules” in the NHS are aluminum oxide quantum
dots with excitons (consisting of spatially separated electrons and
holes) localizing over their surfaces. The interaction of the excitons
with the QD surfaces (“intramolecular” interaction) is shown to be
much stronger than that between quantum dots (“intermolecular”
interaction).
have demonstrated
that in such a NHS (with the mean radius 1 a = 3.18 nm and the
distance between surfaces of aluminum oxide QD D1 = 2.93 nm)
at temperatures lower than the critical temperature Tc = 81.6K
(which corresponds to the exciton quasimolecule binding energy
â E = 7.03 meV) an ,,exciton molecule“ (a biexciton consisting of
spatially separated electrons and holes) can be formed. Acting
as “exciton molecules” in the NHS are aluminum oxide quantum
dots with excitons (consisting of spatially separated electrons and
holes) localizing over their surfaces. The interaction of the excitons
with the QD surfaces (“intramolecular” interaction) is shown to be
much stronger than that between quantum dots (“intermolecular”
interaction).
We have also shown that the position of the biexciton band in the NHS depends both on the QD mean radius 1 a and the distance D1 between QD surfaces. By varying these parameters, one can purposefully control the position of the energy band of biexciton states in the NHS. With increase in temperature above the threshold (Т ≥ Tc), a phase transition can occur from the biexciton to exciton state. It has been found that at a constant concentration of excitons (i.e. constant concentration of QD) and temperatures Т below Tc, one can expect a new luminescence band shifted from the exciton band by the value of the biexciton binding energy â E . This new band disappears at higher temperatures (Т ≥ Tc). At a constant temperature below Tc, an increase in exciton concentration (i.e. in QD concentration) brings about weakening of the exciton luminescence band and strengthening of the biexciton one.
Thus, NHS made up of “exciton molecules” are of considerable interest both physically and practically as novel nanomaterials for nano-optoelectronics [34-42].
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Alferov ZI (2001) Nobel Lecture: The double heterostructure concept and its applications in physics, electronics, and technology. Rev Mod Phys 73(3): 767.
- Ekimov A, Hache F, Schanne-Klein M, D Ricard, C Flytzanis, et al. (1994) Absorption and intensity-dependent photoluminescence measurements on CdSe quantum dots: assignment of the first electronic transitions: erratum. J Opt Soc Amer B 11(3): 524-524.
- Bondar N, Brodin M (2010) Evolution of exciton states near the percolation threshold in two-phase systems with II–VI semiconductor quantum dots. Semiconductors 44(7): 884-892.
- Kulchin Yu N, Shcherbakov AV, Dzyuba VP, Voznesenskii SS, Mikaelyan GT (2008) Nonlinear-optical properties of heterogeneous liquid nanophase composites based on high-energy-gap Al2O3 Quantum Electr 38(2): 154.
- Dzyuba VP, Krasnok AE, Kulchin Yu N (2010) Nonlinear refractive index of dielectric nanocomposites in weak optical fields. Techn Phys Lett 36(11): 973-977.
- Pokutnyi SI (2007) Excition states in semiconductor quantum dots in the modified effective mass approximation. Semiconductors. 41(11): 1323-1328.
- Pokutnyi SI (2013) On an exciton with a spatially separated electron and hole in quasi-zero-dimensional semiconductor nanosystems. Semiconductors 47(6): 791-798.
- Pokutnyi SI (2013) Binding energy of the exciton of a spatially separated electron and hole in quasi-zero-dimensional semiconductor nanosystems. Technical Physics Letters 39(3): 233-235.
- Pokutnyi SI, Kulchin Yu N, Dzyuba VP (2015) Binding energy of excitons formed from spatially separated electrons and holes in insulating quantum dots. Semiconductors 49(10): 1311-1315.
- Pokutnyi SI (2016) Excitons based on spatially separated electrons and holes in Ge/Si heterostructures with germanium quantum dots. Low Temperature Physics 42(12): 1151.
- Pokutnyi SI (2017) Optical absorption by colloid quantum dots CdSe in the dielectric matrix. Low Temperature Physics 43(12): 1797.
- Pokutnyi SI (2018) Optical spectroscopy of excitons with spatially separated electrons and holes in nanosystems containing dielectric quantum dots. J Nanophoton 12(2): 026013.
- Pokutnyi SI (2018) Exciton spectroscopy with spatially separated electron and hole in Ge/Si heterostructure with germanium quantum dots. Low Temperature Physics 44(8): 819.
- Pokutnyi SI (2018) Exciton spectroscopy of spatially separated electrons and holes in the dielectric quantum dots. Crystals 8(4): 148.
- Pokutnyi SI (2013) Biexcitons formed from spatially separated electrons and holes in quasi-zero-dimensional semiconductor nanosystems. Semiconductors 47(12): 1626-1635.
- Pokutnyi SI, Kulchin Yu N, Dzyuba VP (2016) Biexciton in nanoheterostructures of dielectric quantum dots. J Nanophoton 10: 036008.
- Pokutnyi SI, Kulchin Yu N (2016) Special Section Guest Editorial: Optics, Spectroscopy and Nanophotonics of Quantum Dots. J Nanophoton 10(3): 033501.
- Pokutnyi SI (2016) Biexciton in quantum dots of cadmium sulfide in a dielectric matrix. Technical Physics 61(11): 1737-1739.
- Pokutnyi SI (2016) Excitonic quasimolecules in nanosystems of semiconductor and dielectric quantum dots. Modern Chemistry Applications 4(4): 188.
- Pokutnyi SI (2017) Excitonic quasimolecules in nanosystems of quantum dots. Optical Engineering 56(9): 091603.
- Pokutnyi SI (2017) Biexciton in nanoheterostructures of germanium quantum dots. Optical Engineering 56(6): 067104.
- SI Pokutnyi (2017) Excitonic quasimolecules formed by spatially separated electrons and holes in a Ge/Si heterostructure with germanium quantum dots. J Appl Spectroscopy 84(2): 268-272.
- Pokutnyi SI, Kulchin Yu N, Dzyuba VP (2018) Biexciton states in nanoheterostructures of dielectric quantum dots. J Physics Conference Series 1092(1): 12029.
- Pokutnyi SI (2018) Exciton quasimolecules formed from spatially separated electrons and holes in nanostructures with quantum dots of germanium. Molecular Crystals and Liquid Crystals 674(1): 92-97.
- Yakimov AI, Dvurechensky AV (2001) Effects of electron-electron interaction in the optical properties of dense arrays of quantum dots Ge/Si. JETP 119: 574.
- Grabovskis V, Dzenis Y, Ekimov A (1989) Photoionization of semiconductor microcrystals in glass. Sov. Phys Solid State 31(1): 272.
- Bondar N (2010) Photoluminescence quantum and surface states of excitons in ZnSe and CdS nanoclusters. J Luminescence 130(1): 1-7.
- Ovchinnikov OV, Smirnov MS, Shatskikh TS (2014) Spectroscopic investigation of colloidal CdS quantum dots – methylene blue hybrid associates. J Nanopart Res 16: 2286.
- Dzyuba VP, Kulchin Yu N, Milichko VA (2013) Quantum size states of a particle inside the nanopheres. Advanced Material Research A 677: 42.
- Lalumiure K, Sanders B, Van Loo F (2013) Imput - output theory for waveguide QED with an ensemble of inhomogeneous atoms. Phys Rev A 88: 043806.
- Van Loo F, Fedorov A, Lalumiure K (2013) Photon-mediated interactions between distant artificial atoms. Science 342(6165): 1494-1496.
- Lozovik YE (2014) Electronic and collective properties of topological insulators. Advanc Phys Scienc 57: 653.
- Valiev K (2005) Quantum computers and quantum computing. Advanc Phys Sc 48: 1.
- Pokutnyi SI (2005) Optical nanolaser on the heavy hole transition in semiconductor nanocrystals: Theory. Phys Letter A 342(4): 347-350.
- Pokutnyi SI (2004) Stark effect in semiconductor quantum dots. J Applied Physics 96: 1115.
- Oleg V Ovchinnikov, Tamara S Kondratenko, Irina G Grevtseva, Mikhail S Smirnov, Sergey I Pokutnyi (2016) Sensitization of photoprocesses in colloidal Ag2S quantum dots by dye molecules. J Nanophoton 10(3): 033505.
- Viktor G Klyuev, Denis V Volykhin, Oleg V Ovchinnikov, Sergey I Pokutnyi (2016) Relationship between structural and optical properties in colloidal CdxZn1-xS quantum dots in gelatin. J Nanophoton 10(3): 033507.
- Sergey I Pokutnyi, Oleg V Ovchinnikov, Tamara S Kondratenko (2016) Absorption of light by colloidal semiconducor quantum dots. J Nanophoton 10(3): 033506.
- Pokutnyi SI (2018) Strongly absorbing light nanostructures containing metal quantum dots. J Nanophoton 12(1): 012506.
- Pokutnyi SI, Kulchin Yu N, Amosov AV, Dzyuba VP (2019) Optical absorption by a nanosystem with dielectric quantum dots. Proc SPIE 11024: 1102404.
- Pokutnyi SI (2015) Exciton states formed by spatially separated electron and hole in semiconductor quantum dots. Technical Physics 60(11): 1615-1618.
- Pokutnyi SI (2015) Spectroscopy of quasiatomic nanostructures. J Optical Technol 82(5): 280-285.
-
Sergey I Pokutnyi. Exciton Quasimolecules and Exciton Quasicrystals: Theory. Mod Concept Material Sci. 2(2): 2019. MCMS. MS.ID.000534.
-
Electrons, Holes, Biexciton ground singlet states, Binding energy, Coulomb, Polarization and exchange interaction, Quantum dots, Nanoheterostructures
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






