Brief Overview on the Application of Finite Element Method on Flat Rolling Processes

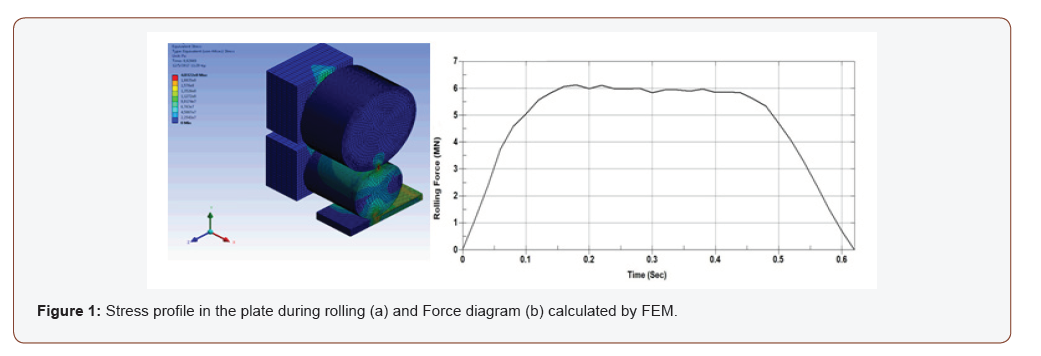
Amongst forming, flat rolling processes consist most of the selected methods for all applied technical alloys and materials used in various applications. Flat rolling is a bulk forming process where a metal plate or strip passes through counter rotating rolls and deforms plastically to reduce its thickness. Complicated phenomena take place in the material and the mill during their interaction, which in turn have a significant influence on the quality of the final product. Many tools have been developed through the years that would help the engineers predict and, thus, control the process result. A very prominent and widely used computational tool is FEM. The FEM is a numerical technique that discretizes a complicated system into finite simpler systems (finite elements) and solves partial differential equations to approximate the solution. Considering the cost related to industrial trials, the use of FEM has gained great popularity amongst engineers. Figure 1 shows indicative results that are typically extracted when FEM is applied, such as the stress field during rolling, see Figure 1(a), and the calculated Force diagram, see Figure 1(b), which are usually also validated using industrial and/or laboratory/actual data.

Various finite element algorithms that are predominantly based on either static implicit or dynamic explicit formulation are available as commercial packages for the simulation of forming processes. The static implicit method can be very efficient under quasi-static conditions such as in forming processes [1-3]. Large time step size and iterative solution of equations until a convergence criterion is fulfilled ensures high accuracy and time efficiency. Nevertheless, highly non-linear problems with nonlinear materials, local instabilities, frictional sliding, variable and complicated contact conditions, etc. are difficult to be managed resulting to high resource requirements and computational cost. In that case, the time-step becomes minimal with more iterations necessary for every time increment in order to achieve convergence, which in many cases is even impossible to obtain whatsoever [4-12].

The dynamic explicit method was introduced as a solution to the problems. The equation of motion is solved by inversion of mass matrix, a much simpler operation comparing to the inversion of the stiffness matrix that is required in the implicit method. The iterative scheme is superseded by very small time increment to ensure stable solution [12-14]. Time increment is only influenced by the Courant–Friedrichs–Lewy condition, which is mesh size and material property dependent, and is not affected by the complexity of the model and non-linearities [11,12,14]. Nevertheless, stability is obtained only when the maximum time increment is lower than a critical value of the smallest transition times for a dilatational wave to cross any element in the mesh. In simulation of rolling, the time increment can become so small that the time required for the solution of the problem might become unrealistic.

Comparison between the two methods for rolling simulation can be found in literature [15-17]. For plate rolling, although similar accuracy can be obtained between the two methods, the explicit method is a more efficient and stable method for 2D problems comparing to the implicit method [15]. However, more recent developments in the implicit solver for forming processes increased the efficiency of the implicit method to an extent that it became more efficient comparing to the explicit method even in 3D rolling models [16]. Nevertheless, when the 3D model becomes more complicated comprising also of elastic work rolls and support rolls, the explicit method becomes once again more efficient comparing to the implicit method [17].

Through the years, the FEM approach has become an established method for the simulation of rolling process. During rolling, high forces develop between the plate and the rolls and, moreover, temperature gradient evolves both in the plate and the rolls. Those phenomena play important role on the final product quality. In addition to the fact that most rolling plants utilize the same equipment for rolling a wide range of materials with various levels of mechanical properties, initial geometry of the plate and final specifications, force and temperature evolution are the fundamental questions that trouble the production engineers during the pass schedule design. Both parameters, including stress and strain profiles, can successfully be computed by the FEM that provides that valuable information even from the early steps [18- 32].

Further utilization of the FEM enabled the simulation of various other quality characteristics. A lot of attention has drawn the shape optimization and the flatness improvement. The strip profile (crown) is correlated with the deflection of the roll stack and can be controlled by counter bending the rolls using integrated systems. Information of the crown can originate from FEM calculation and can be incorporated in the pass schedule design [33-41]. The same applies for the optimization edge profile which is significant for the reduction of edge cracks and edge material removal retaining the same equipment [16,42-43]. The crack initiation as well as other undesirable phenomena occurring during rolling such as wear and plate refusal have likewise been studied by FEM [44-46].

Temperature evolution and gradient caused by heat flux from the strip to the roll have also an effect on the process and the material quality. The work rolls temperature state has a direct impact on its instantaneous geometry and, therefore, on the products flatness. Many researchers have focused on the prediction of thermal camber and the methodology for heat extraction through cooling [47-51].

On the other hand, temperature in the material facilitates the beginning of microstructural changes. Many efforts have been made to integrate algorithms in FEM models that consider the metallurgical aspects that cause the material to soften with time via recovery and recrystallization, to harden via phase transformations or precipitation and to alter its texture and anisotropy [52-56].

For practical purposes, this mini report briefly reviewed the most commonly used applications of FEM analysis as emerged throughout the years regarding flat rolling. The FEM not only allowed engineers to better understand the rolling process itself, but also to accurately predict the influence of critical process conditions such as thermal and mechanical interaction, tribological conditions, material properties and related microstructural phenomena on the product’s final quality. Therefore, FEM can and is nowadays used as a tool to optimize the rolling process and to reduce the production cost.

None.

No conflict of interest.

1. Gelin JC, Boulmane L, Boisse P (1995) Quasi-static implicit and transient explicit analyses of sheet-metal forming using a C⁰ three-nodes shell element. Journal of Material Processing Technology 50(1-4): 54-69.
2. Sun JS, Lee KH, Lee HP (2000) Comparison of implicit and explicit finite element methods for dynamic problem. Journal of Material Processing Technology 105(1-2): 110-118.
3. Yang D, Jung D, Song I, Yoo D, Lee J (1995) Comparative investigation into implicit, explicit, and iterative implicit/explicit schemes for the simulation of sheet-metal forming processes. Journal of Material Processing Technology 50(1-4): 39-53.
4. Van den Boogaard AH, Rietman AD, Huétink J (1998) Iterative solvers in forming process simulations, Proceedings of the 6th International conference on Numerical Methods in Industrial forming processes - Numiform '98, Rotterdam, Balkema, Enschede, pp. 219-224.
5. Kacou S, Parsons ID (1993) A parallel multigrid method for history-dependent elastoplasticity computations. Computer Methods in Applied Mechanics and Engineering 108(1-2): 1-21.
6. Mahnken R (1995) A Newton-multigrid algorithm for elasto-plastic/viscoplastic problems. Computational Mechanics 15(5): 408-425.
7. Jefferson AD, Thomas HR (1997) Convergence criteria for iterative solvers applied to nonlinear plasticity problems, 5th International conference on Computational plasticity: fundamentals and applications – COMPLAS '97, Spain, 1997, CIMNI, Barcelona, pp. 441-446.
8. Ferencz RM, Hughes TJR (1998) Iterative finite element solutions in nonlinear solid mechanics. Handbook of numerical analysis 6: 3-178.
9. Demarco D, Dvorkin EN (2001) Modeling of metal forming processes: implementation of an iterative solver in the flow formulation. Computers & Structures 79(20-21): 1933-1942.
10. Mocellin K, Fourment L, Coupez T, Chenot JL (2001) Toward large scale F.E. computation of hot forging process using iterative solvers, parallel computation and multigrid algorithms. International Journal for Numerical Methods in Engineering 52(5-6): 473-488.
11. Pauskar PM, Sawamiphakdi K, Jin DQ (2004) Static Implicit vs. Dynamic Explicit Finite Element Analysis for Ring Rolling Process Modeling. AIP Conference Proceedings, pp. 721: 412.
12. Prior AM (1994) Applications of Implicit and Explicit Finite Element Techniques to Metal Forming. Journal of Material Processing Technology 45(1-4): 649-656.
13. Mattiasson K, Bernspång L, Honecker A, Schedin E, Hamman T, et al. (1991) On the use of explicit time integration in finite element simulation of industrial sheet metal forming processes. In Numerical simulations of 3D Sheet Forming Processes, Dusseldorf, VDI-Berichte, VDI Verlag GmbH, pp. 479-498.
14. Mercer CD, Nagtegaal JD, Rebelo N (1995) Effective application of different solvers to forming simulations, Simulation of Materials Processing: Theory, Methods and Applications, Proceedings of International conference on Numerical Methods in Industrial forming processes - Numiform '95, Rotterdam, 1995, Balkema, Enschede, pp. 469-474.
15. Lindgren LE, Edberg J (1990) Explicit versus Implicit Finite Element Formulation in Simulation of Rolling. Journal of Materials Processing Technology 24: 85-94.
16. Simon P, Falkinger G, Scheiblhofer S (2017) Hot Rolling Simulation of Aluminum Alloys using LS-Dyna, 11th European LS-DYNA Conference 2017, Salzburg, Austria.
17. Gavalas E, Pressas I, Papaefthymiou S (2019) Mesh sensitivity analysis on implicit and explicit method for rolling simulation, International Journal of Structural Integrity 9(4): 465-474.
18. Le Mat N, Beynon JH, Ponter ARS, Yiu HL (1994) Thermomechanical Modelling of Aluminium Alloy Rolling. Journal of Materials Processing Technology 45(1-4): 631-636.
19. Duan X, Sheppard T (2001) Prediction of temperature evolution by FEM during multi-pass hot flat rolling of aluminium alloys. Modelling and Simulation in Materials Science and Engineering 9: 525-538.
20. Bagheripoor M, Bisadi H (2011) Effects of rolling parameters on temperature distribution in the hot rolling of aluminum strips. Applied Thermal Engineering 31(10): 1556-1565.
21. Duan X, Sheppard T (2002) Three dimensional thermal mechanical coupled simulation during hot rolling of aluminium alloy 3003, International Journal of Mechanical Sciences 44(10): 2155-2172.
22. Jiang ZY, Tieu AK, Lu C, Sun WH, Zhang XM, et al. (2004) Three-dimensional Thermo-mechanical Finite Element Simulation of Ribbed Strip Rolling with Friction Variation. Finite Elements in Analysis and Design 40(9-10): 1139-1155.
23. Lin ZC, Shen CC (2001) A coupled finite element method for a three-dimensional analysis of the flat rolling of aluminum with different reductions. Journal of Materials Processing Technology 110(1): 10-18.
24. Pesin A, Pustovoytov D (2016) Heat transfer modeling in asymmetrical sheet rolling of aluminium alloys with ultra-high shear strain. NUMIFORM 2016, MATEC Web of Conferences 80: 04005.
25. Phaniraj MP, Behera BB, Lahiri AK (2005) Thermo-mechanical modeling of two phase rolling and microstructure evolution in the hot strip mill Part I. Prediction of rolling loads and finish rolling temperature. Journal of Materials Processing Technology 170(1-2): 323-335.
26. Riahifar R, Serajzadeh S (2007) Three-dimensional model for hot rolling of aluminum alloys. Materials & Design 28(8): 2366-2372.
27. Shahani AR, Setayeshi S, Nodamaie SA, Asadi MA, Rezaie S (2009) Prediction of influence parameters on the hot rolling process using finite element method and neural network. Journal of materials processing technology 209(4): 1920-1935.
28. Tieu AK, Jiang ZY, Lu C (2002) A 3D finite element analysis of the hot rolling of strip with lubrication. Journal of Materials Processing Technology 125-126: 638-644.
29. Tseng AA (1999) thermal modeling of roll and strip interface in rolling processes: part 2-simulation, Numerical Heat Transfer, Part A: Applications: An International Journal of Computation and Methodology 35(2): 135-154.
30. Yoon SJ, Shin TJ, Lee JS, Hwang SM (2017) Three-Dimensional Finite Element Analysis of Skin-Pass Rolling and New Models for Process Control. Journal of Manufacturing Science and Engineering 139(9).
31. Zhou L, Huang ZY, Wang CZ, Zhang XX, Xiao BL, et al. (2016) Constitutive flow behavior and finite element simulation of hot rolling of SiCp/2009Al composite, Mechanics of Materials 93: 32-42.
32. Misovic M, Tadic N, Jacimovic M, Janjic M (2016) Deformations and velocities during the cold rolling of aluminium alloys. Materials and technology 50(1): 59-67.
33. Chao L, Anrui H, Yi Q, Defu G, Jian S (2019) Effect of Internal Stress of Incoming Strip on Hot Rolling Deformation Based on Finite Element and Infinite Element Coupling Method. Metals 8(2): 92.
34. Sun WQ, Li B, Shao J, He AR (2016) Research on crown and flatness allocation strategy of hot rolling mills. Int J simul Model 12(2): 327-340.
35. Linghu K, Jiang Z, Zhao J, Li F, Wei D, et al. (2014) 3D FEM analysis of strip shape during multi-pass rolling in a 6-high CVC cold rolling mill. The International Journal of Advanced Manufacturing Technology 74: 1733-1745
36. Gautam V (2013) Finite element analysis of deflection of rolls and its correction by providing camber on rolls. International Journal of Research in Aeronautical and Mechanical Engineering 1(6): 42-47.
37. Shigaki Y, Montmitonnet P, Silva JM (2017) 3D finite element model for roll stack deformation coupled with a Multi-Slab model for strip deformation for flat rolling simulation, AIP Conference Proceedings 1896: 190018.
38. Gavalas E, Papaefthymiou S (2019) Prediction of Plate Crown during Aluminum Hot Flat Rolling by Finite Element Modeling. Journal of Manufacturing and Materials Processing 3(4): 95.
39. Wang T, Xiao H, Zhao TY, Qi XD (2012) Improvement of 3-D FEM Coupled Model on Strip Crown in Hot Rolling. Journal of Iron and Steel Research International 19(3): 14-19.
40. Sikdar S, Shylu J, Pandit A, Dasu R (2007) Analysis of roll stack deflection in a hot strip mill. J Braz Soc Mech Sci & Eng 29(3).
41. Guo RM (1989) Determination of Optimal Work Roll Crown for a Hot Strip Mill. Iron and Steel Technology 66(8): 52-60
42. Rout M, Pal SK, Singh SB (2019) Prediction of edge profile of plate during hot cross rolling. Journal of Manufacturing Processes 31: 301-309.
43. Yu H, Liu X, Chen L, Li C, Zhi Y, et al. (2009) Influence of Edge Rolling Reduction on Plate-Edge Stress Distribution During Finish Rolling. Journal Of Iron and Steel Research International 16(1): 22-26.
44. Cao J, Liu S, Zhang J, Song P, Yan T, et al. (2011) ASR work roll shifting strategy for schedule-free rolling in hot wide strip mills. Journal of Materials Processing Technology 211(11): 1768-1775.
45. Pesin A, Pustovoytov D, Shveyova T, Sverdlik M (2015) Finite Element Modeling of Roll Wear during Cold Asymmetric Sheet Rolling of Aluminum Alloy 5083. MATEC Web of Conferences 26: 01010.
46. Ognjanovic R, Waterson K (2003) Finite element analysis modeling of ingot refusal conditions during the rolling process. Computers and Structures 81(8-11): 871-877.
47. Trull M, McDonald D, Richardson A, Farrugia D (2006) Advanced finite element modelling of plate rolling operations. Journal of Materials Processing Technology 177(1): 513-516.
48. Bao L, Qi XW, Mei RB, Zhang X, Li GL (2019) Investigation and modelling of work roll temperature in induction heating by finite element method. Journal of the Southern African Institute of Mining and Metallurgy 118(7): 735-743.
49. Guo ZF, Li CS, Xu JZ, Liu XH, Wang GD (2006) Analysis of temperature field and thermal crown of roll during hot rolling by simplified FEM. J Iron Steel Res Int 12(6): 27-30.
50. Benasciutti D, Brusa E, Bazzaro G (2010) Finite element prediction of thermal stresses in work roll of hot rolling mills. Proc Eng 2(1): 707-716.
51. Li C, Yu H, Deng G, Liu X, Wang G (2007) Numerical Simulation of Temperature Field and Thermal Stress Field of Work Roll During Hot Strip Rolling. Journal of Iron and Steel Research 14(5): 18-21.
52. Engler O, Karhausen K, Hirsch J (2009) Simulation of Microstructure and Texture Evolution in Aluminum Sheet. ASM Handbook: Fundamentals of Modeling for Metals Processing 22A: 510-521.
53. Shabaniverki S, Serajzadeh S (2016) Simulation of softening kinetics and microstructural events in aluminum alloy subjected to single and multi-pass rolling operations, Applied Mathematical Modelling, 40(17-18): 7571-7582.
54. Li XT, Wang MT, Du FS (2008) Coupling Thermomechanical and Microstructural FE Analysis in Plate Rolling Process. Journal of Iron and Steel Research International 15(4): 42-50.
55. Seyed Salehi M, Serajzadeh S (2013) Simulation of static softening behavior of an aluminum alloy after cold strip rolling. Computational Materials Science 69: 53-61.
56. Falkinger G., Simon P (2017) Static recovery of an AlMg4.5Mn aluminium alloy during multi-pass hot-rolling, International Conference on the Technology of Plasticity, ICTP 2017, Cambridge, United Kingdom, Procedia Engineering 207: 31-36.