Application of DLVO Theory on the Interaction Forces for Rheology of Coal-Water Slurries

Based on the depletion of present fuel reserves in the world, many investigations are carried out for finding alternatives. Thus, coal-water slurries (hereafter CWS) is one of these alternatives that consists of finely dispersed coal particles suspended in water. A commercial CWS includes 55-70% fine coal, 25-40% water and 1% chemical additive [2] while these values are effective on the basic characteristics like viscosity, density and fluidity of mixtures that constitute their quality and selling conditions. As well known, the flow and the stability characteristics vary upon physical and physicochemical properties of coal suspensions, regarding volume fraction of solids, particle size, size distribution, temperature, concentration of salt and thus particle-particle interactions in mixture. Therefore, modeling of these interactions is significant for determining the relevant characteristics of suspensions by means of the movement of very fine particles dominated by surface forces [3]. In this manner, DLVO theory (Derjaguin-Landau-Vier-Overbeek theory) is the most commonly used assumption consisting of attractive London van der Waals and repulsive electrostatic double layer forces for modeling the colloidal dispersion stability. Figure 1 shows a typical potential energy vs. separation distance (h) for particle-particle interaction.

V_TOT shows the energy barrier which is used to define the maximum repulsion between particles. When the height of this energy barrier is high, particles will be in the dispersed form while they will coalesce at lower heights [3,5].

In consequence, the aim of this study is to model the coal particle interactions by classical DLVO theory and suggest a correlation between their rheological indices and theoretical energy barrier.

As mentioned in “Introduction” section, only the modelling of reported values and accordingly their responses as barrier heights were examined in this study. Therefore, both the characteristics of samples and other experimental measurements were prepublished, and the methods were extensively explained in aforementioned papers [2]. However, in order to give introduction about the materials characteristics and methods, both the methods and the outputs from these tests were briefly explained and reevaluated with relation to their calculated energy barrier heights.

Materials

In modeling studies, the zeta potential and rheological characteristics of coal samples from Soma, Ağaçlı and Siberia [2] were used. Proximate analyses and other characteristics of samples were shown in Table 1. The chemicals used were PSS (sodium polystyrene sulfate) as dispersant agent and CMC-Na (carboxyl methyl cellulose) as stabilizer. Based on the findings published in a previous publication, concentrations of chemicals were selected as 1% of suspensions comprised of 90% PSS and 10% CMC-Na [1] (Table 1).

These values indicated that while Siberia and Soma coals presented low ash contents within the range of 6-8 %, Ağaçlı coal exhibited the highest ash content as 14.43% associated with its inherent moisture. On the other hand, while upper calorific value of Siberia and Soma coals were relatively close, their total sulfur, volatile matter and fixed carbon contents were quite different which pointed out the difference of their rank. Apart from their proximate analysis, particle size, porosity and specific surface area are other features of these samples for modelling. Thus, the values of these parameters were given in Table 2.

Table 1:Proximate and Ultimate Analysis of coal samples on dry base (Values were retrieved from Boylu et al. [1].

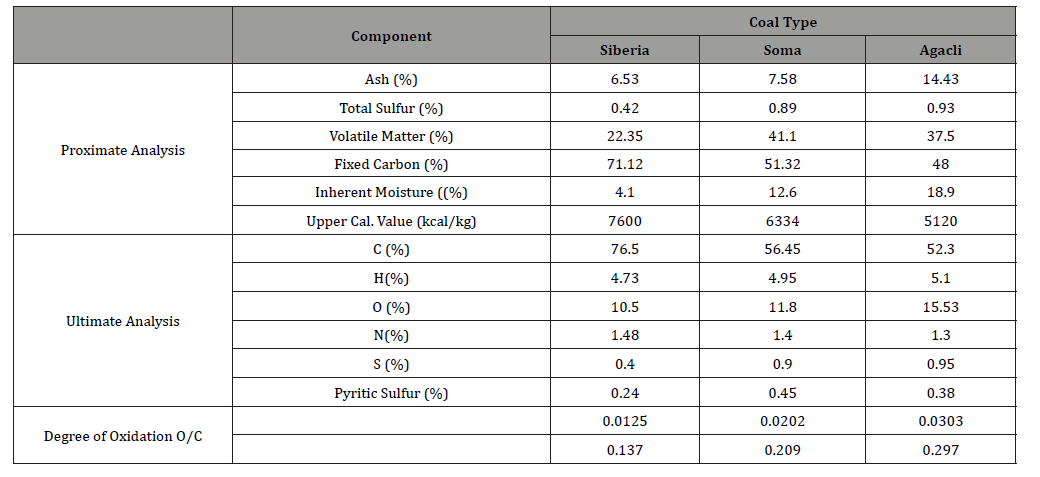
Table 2:Physical properties of coal samples [1].

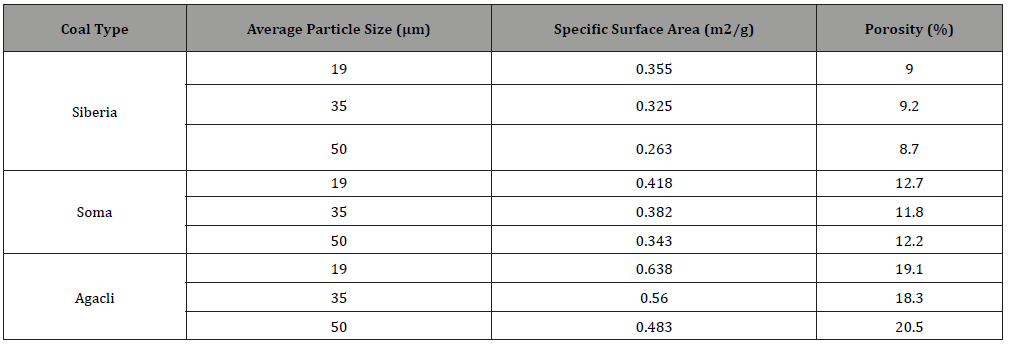
As shown in Table 2, the specific surface area linearly decreased upon increasing particle size for all coal samples. But their porosity followed a different trend which can be attributed to their different structure.

Methods

As mentioned above, the procedures for zeta potential and viscosity measurements were extensively explained in a previous publication [2]. But if a brief explanation were given for each method.

Zeta potential was measured by Zeta Meter 3.0 instrument. And during these measurements, about 0.1 g of coal sample was conditioned in a 100-ml solution containing 0.001 M KCl in order to stabilize the ionic balance of solution. Then it was conditioned for 10 minutes during which the pH of the solution was adjusted with NaOH or HCl solution. Zeta potential of particles in the presence of reagents were also measured and the average of ten measurements were presented for each sample [2].

Viscosity measurements were performed with RVD2-Brookfield rotating type viscometer in a distilled water at 1200 rpm mixing speed. In all experiments, the pH of the slurry varied in the range of 7.05 to 7.25 and the temperature was kept constant within 25±2 °C.

Theoretical calculations

According to the increasing importance of interactions like adsorption, coagulation, flotation between particle-plate and particle-bubble, etc. [3,6,7], numerous attempts have been performed in order to calculate the energy barrier height mostly by the pioneering works of Derjaguin, Landau, Verwey, Overbeek (DLVO) first published in 1942. In literature, the effects of different parameters like electrolyte concentration, pH, particle size, reagent type for these interactions on different processes like flotation [3,8], coagulation [9], dispersion, aggregation were studied, however to our knowledge only a few of them addressed the relation between rheological indices of particles by their interaction degrees with each other [10]. Considering this lack of knowledge in mind, in modeling studies, besides other well-known parameters like permittivity of water, Boltzmann constant, the values of zeta potential measurements and average particle size of samples were used. In these calculations, the total interaction energy, between two particles was calculated as the sum of electrostatic double layer energy (V_EDL) and London van der Waals dispersion energy (V_vdW) components.

London van der Waals force between coal particles in water is always attractive according to the electric and magnetic polarizations. Despite many equations presented in literature, Hamaker’s method is the simplest one that the value of vdW force for identical spheres with the same radii is expressed by,

Where, A_H represent the Hamaker constant (J) for two particles (1) acting across the medium (2), “a” is the radius of particle and h is the separation distance between two spherical particles. In addition, it is worth to note that this equation is valid if the radius of the particle (a) is higher than separation distance (h).

Electrical double layer forces between two particles with constant surface potential (Ψδ) follow the expression (with error up to 40 %) below (Berg, J. 2010 as cited in Li, 2012).

In this equation, ε is the permittivity of water, κ is the thickness of double layer, Ψ_δ is the stern plane potential where zeta potential is commonly used instead of these ones. When considered, the calculation of energy barrier heights between particles provides both the optimized conditions of interactions in a pre-defined medium and degrees of coagulation or dispersion which are very important for obtaining suitable conditions for CWS rheology [7,10].

Zeta potential of coal samples

The zeta potential of different coal samples with/without reagent was plotted against pH in Figure 2. It was observed that generally all coal samples followed a negative trend as a function of pH. Apart from Siberia coal, the i.e.p of other coal samples was found between pH 1.5 and 3. Another point to discuss is that upon the introduction of reagent for all coals, the zeta potential values became more negative at all pH values. This situation also indicated that negative sides of reagents were adsorbed onto coal surfaces and made them more negative along with the increasing OH- ions in system. At that point, particles also became more dispersed with the dominancy of repulsive forces and became unstable upon adsorption of a certain concentration of reagent.

As well known, the variation on zeta potential values will change the electrostatic forces between particles. In other words, upon increasing the zeta potential value, the characteristics of total interaction may result in dispersion of particles. As it can be seen from Figure 2 while Soma and Siberia coals exhibited a similar trend after treatment with reagent in their original pH value (around 7), due to their similar ash content and type. It is worth to note that Ağaçlı coal presented more positive values under the same pH value based on its structural difference.

The viscosity values of CWS comprising of different coal samples was measured at original pH value (close to 7) at different particle size ranges as 19, 35 and 50 microns. The values of these measurements were reported in a previous publication [2] and shown in Table 3.Rheology measurements of CWS

Table 3:Results of viscosity measurements (taken from Boylu et al. [1]) as a function of particle size.

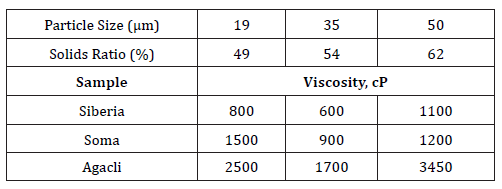
The viscosity values shown in Table 3 also indicated that higher solids rate % is required in case of coarser sizes. However, viscosity of suspensions followed a variable trend that while the lowest viscosity values were obtained at 35μm for all samples, higher viscosity values were obtained when the particle size decreased to 19μm. In addition to that finding, viscosity of suspensions followed an ascending trend between Siberia and Agacli coal samples. When considered, these values were in line with their porosity and specific surface areas at different size ranges which indicated that the dispersion of particles is directly based on physical characteristics. In contrast, at constant viscosity value, lower specific surface area of particles resulted in higher solids ratio for obtaining optimum conditions for viscosity.

Energy barrier calculations

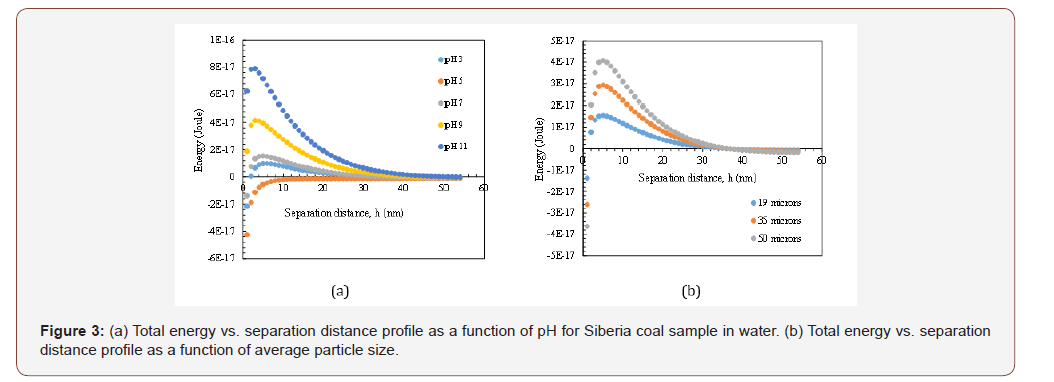
In Figures 3a and 3b, variations on energy were shown for Siberia coal in water. As it can be seen from Figure 3a, the lowest energy barrier (-2.43x 10-18 J) was obtained at pH value close to the i.e.p. as previously shown in Figure 2. This is an expected situation because when the surface charge between particles become near zero, the repulsive forces generally disappears, and attractive ones become dominant while particles start to form coagulates under these conditions. But in terms of viscosity, the profile may be different which can be ascribed to main two reasons (i) considering the particle size in micron range, zeta potential values of particles will not be as effective on viscosity as they are at finer sizes. (ii) Since the settlement will occur with the help of gravity, the variation on this situation became only the result of theoretical calculations. So, when the viscosity of system is considered then it may lead to increase the low shear viscosity at high concentrations for micron sized particles [11] (Figure 3&4).

*In Figures 3a and 4a, the particle size was 19 microns, Hamaker Constant (A₁₃₂) was 3x10_-20 J and thickness of double layer 1x10₈ nm

It is worth to note that even the particles seem to form coagulates theoretically at isoelectric point, in real conditions they may express different characteristics which are not in line with these calculated ones. On the other hand, considering the energy barriers in other pH values, it is clear that particles became more dispersed (energy increased to 7.89x10-17 J at pH 11 shown in Figure 3a) due to the higher zeta potential values (absolute values) under same conditions as Hamaker constant, thickness of double layer. Meanwhile, if only particle size is considered (Figure 3b), decreasing the particle size resulted in lower energy barriers as a result of mathematical calculations and in line with lower viscosity values (see Table 3). Thus, in order to investigate the effects of reagent addition for this system, energy barriers were re-calculated by considering their zeta potential values and particle sizes.

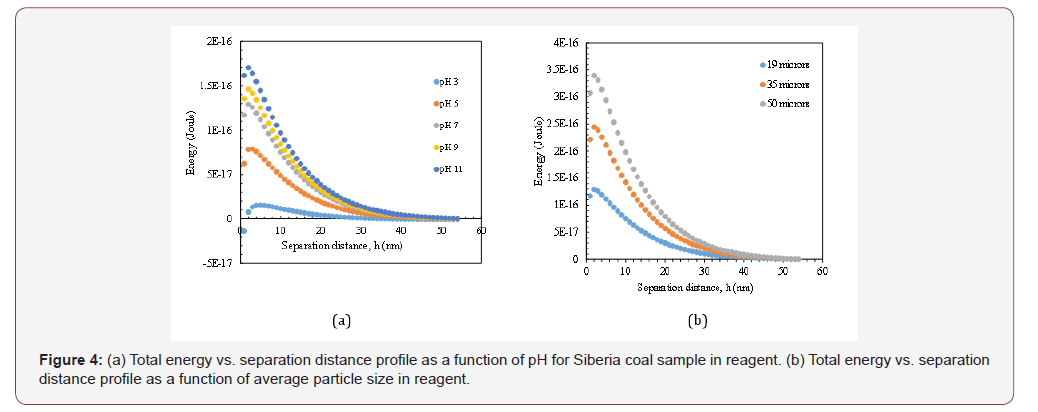
As it was shown in Figure 4a, upon introduction of reagent to the suspension, the total energy profile between particles significantly changed and repulsive forces became dominant at all pH values upon increasing dispersion. In this manner, the energy barrier in pH: 11 increased to 1.70x10_-16 J from 5.31x10_-17 J as reported for the same pH value before addition. Despite the unstable state of particles (zeta potential lower than -30 mV) this situation can be explained by the adsorption characteristics of reagent on mixed structure of coal surfaces. In addition, as mentioned in the methods section, all rheological measurements were performed in their original pH value ≈7, so regarding those calculated energy profiles, it is worth to note that, although the particle size is not effective at zero point of charge, it became very important when particles were in their original pH value (see Figures 3b and 4b). From these figures, it can be also understood that increasing the particle size resulted in higher energy barrier (3.39x10_-16 J), which in turn more dispersed particles and higher viscosity which are in line with the values shown in Table 3. However, the energy barrier for 35μm followed a different trend which is not in accordance with the measured viscosity values.

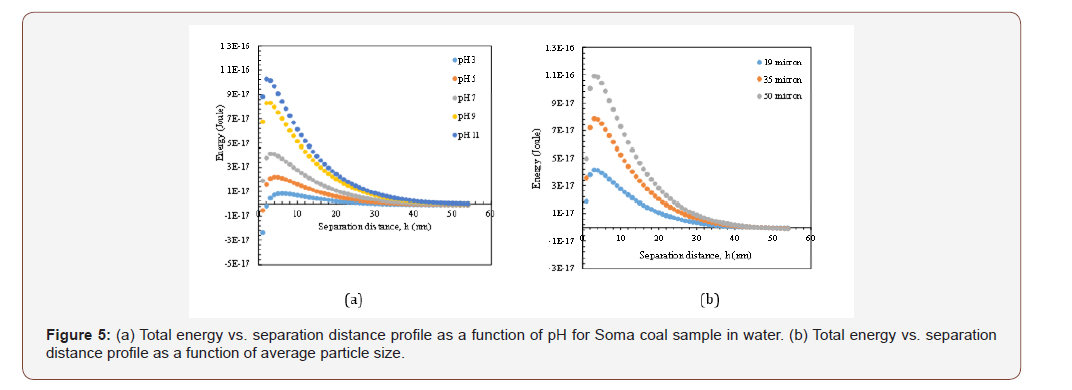
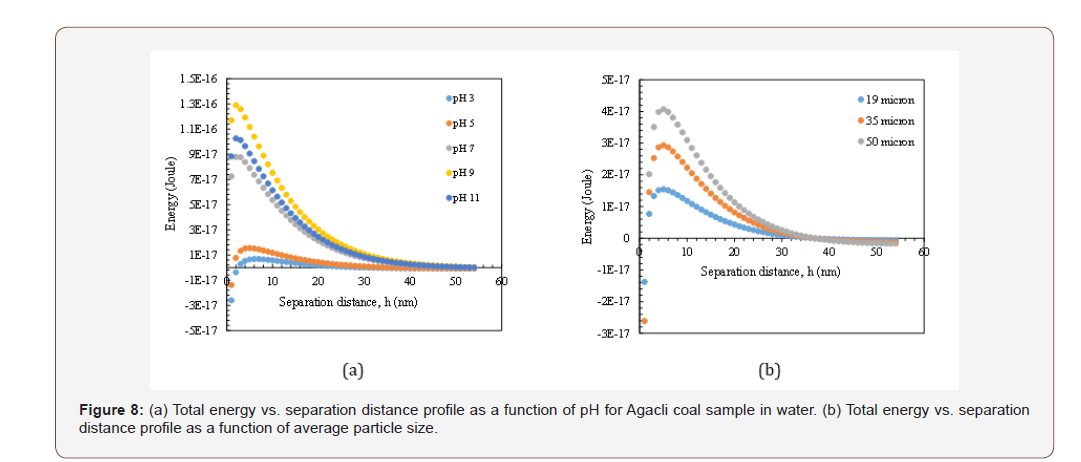
Following the calculations for Siberia coal, the same procedure was applied for other coal samples as Soma and Ağaçlı regions and the results were shown in Figures 5a-b to 8a-b. As Figure 5a reveals, the lowest energy barrier (8.34x10-18 J) was found at pH 3 for Soma coal which was in line with the zeta potential values given in Figure 2. And the highest energy barrier was obtained at pH 11 (1.02x10- 16 J) which is negligibly lower compared to Siberia. As discussed in the previous sample, this difference could well be ascribed to the structural differences and in with their lower viscosity values (Figure 5&6).

*In Figures 5a and 6a, the particle size was 19 microns, Hamaker Constant (A₁₃₂) was 3x10_-20 J and thickness of double layer 1x108 nm

As shown in Figures 5b and 6b, increasing the particle size resulted in high energy barrier as 1.09x10-16 J at 50 microns at original pH value with/without reagent. However, the relationship between viscosity and energy barrier is not all proportional like Siberia coal. In other words, when the energy barrier decreased to 4.11x10-17 J for 19μm size range, the viscosity of CWS was found as 1500 cP but when the energy barrier increased to 1.09x10-16 J, the viscosity of suspensions decreased to 1200 cP. This is an unexpected situation however considering the other components as hydration and hydrophobic forces (which will be discussed in a further submission) and mixed adsorption characteristics of reagent on coal surfaces, this result became acceptable (Figure 7&8).

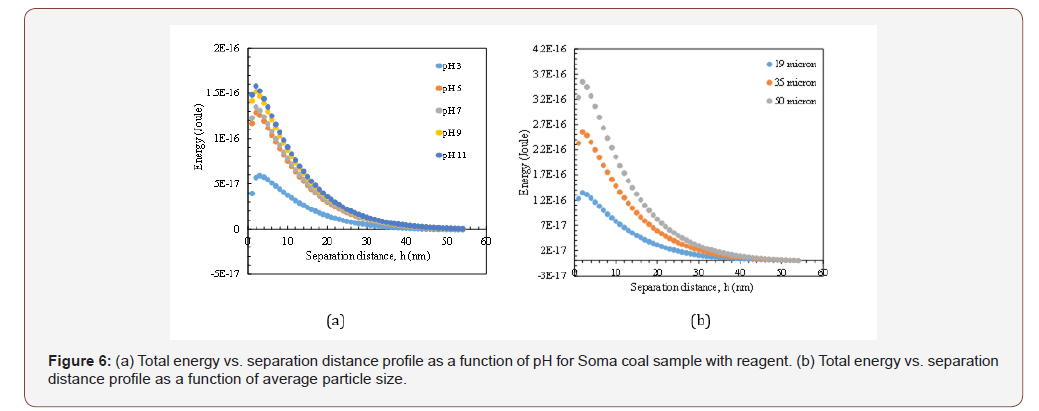
*In Figures 5a and 6a, the particle size was 19 microns, Hamaker Constant (A₁₃₂) was 3x10_-20 J and thickness of double layer 1x108 nm

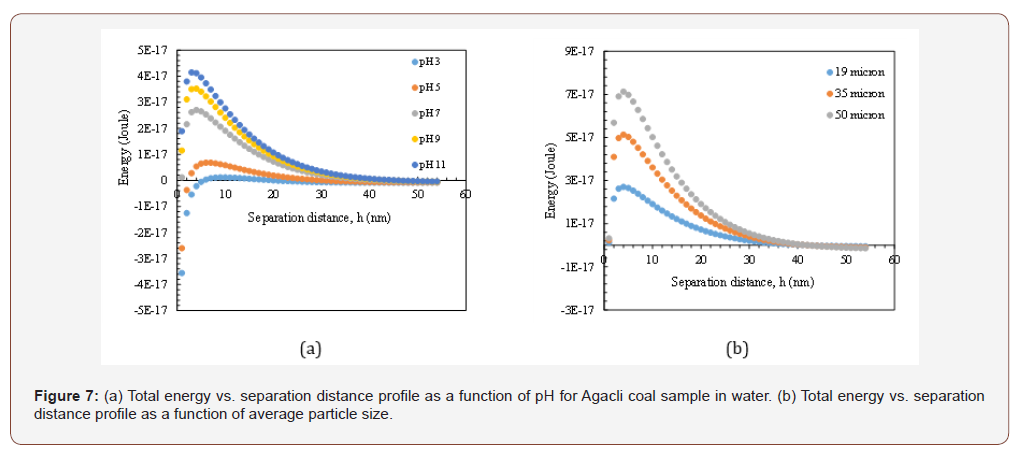
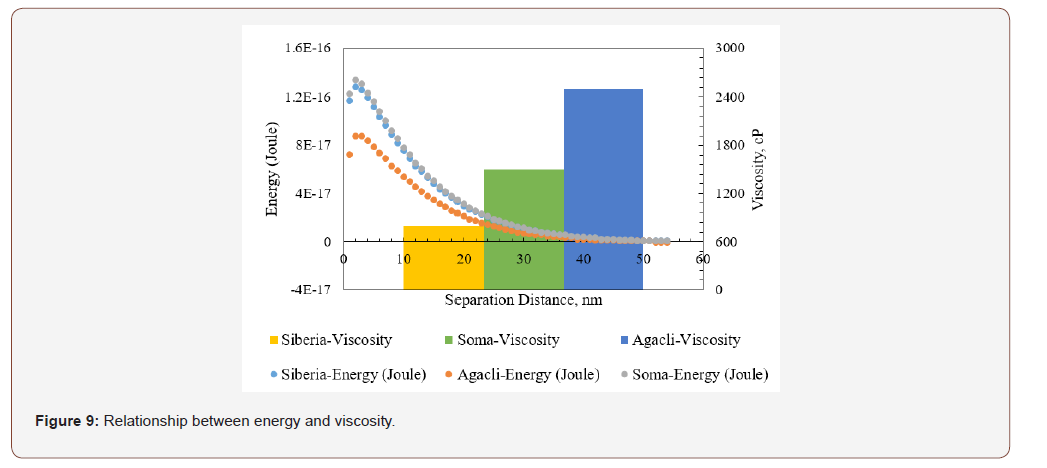
Similar dependencies were obtained for Soma and Agacli coal samples. As demonstrated in Figure 8b, the highest energy barrier was found 3.98x10-17 J which indicated higher viscosity characteristics that was in line with the values given in Table 3. Thus, if the optimum points were shown in the same graph for all samples (Figure 9), then one can conclude that in contrast to their individual characteristics, upon increasing the energy barrier for each sample, their viscosity will increase based on their physical properties such as porosity and specific surface area.

** The particle size was 19 microns, Hamaker Constant (A₁₃₂) was 3x10-20 J and thickness of double layer 1x10⁸ nm

The rheological indices of different coal samples were determined in the presence of PSS and CMC-Na at their original pH 7-7.4. It was found that the viscosity values of particles follow a linear trend with their specific surface area and porosity values at all sizes.

The calculated energy barrier between particles indicated that the energy barrier between particles decreases as they approach to their iso-electric point. In addition, it was also found that by increasing energy barrier between particles, their condition changed to dispersion mode which make them more suitable for producing CWS.

Overall results for whole samples showed that in contrast to their individual characteristics about viscosity and energy barrier, lower energy barriers resulted in higher viscosity values which in turn suggesting the effects of other physical parameters or the need for adding other force components to calculations.

None.

No conflict of interest.

1. Boylu F, Dinçer H, Ateşok G (2004) Effect of Coal Particle Size Distribution, Volume Fraction and Rank on The Rheology of Coal-water Slurries. Fuel Processing Technology 85(4): 241-250.
2. Atesok G, Boylu F, Sirkeci AA, Dinçer H (2002) The Effect of Coal Properties on the Viscosity of Coal-water Slurries. Fuel 81(14): 1855-1858.
3. Guven O, Celik MS, Drelich JW (2015) Flotation of methylated roughened glass particles and analysis of particle-bubble energy barrier. Minerals Engineering 79: 125-132.
4. Cardellini A, Fasano M, Bigdeli BM, Chiavazzo E, Asinari P (2016) Thermal transport phenomena in nanoparticle suspensions. J Phys Condens Matter 28(48): 483003.
5. Honaker RQ, Ozsever AV, Parekh BK (2006) Selective detachment process in column flotation froth. Minerals Engineering 19(6-8): 687-695.
6. Laskowski JS, Xu Z, Yoon RH (1992) Energy barrier in particle-to-bubble attachment and its effect on flotation kinetics. Mines & Carrieres Les Techniques 74: 95-100.
7. Pineres J, Barraza J (2011) Energy Barrier of aggregates coal particle-bubble through the extended DLVO theory. International Journal of Mineral Processing 100(1-2): 14-20.
8. Drelich J, PK Bowen (2015) Hydrophobic nano-asperities in control of energy barrier during particle-surface interactions. Surface Innovations 3(3): 164-171.
9. Xu Z, Yoon RH (1989) The Role of Hydrophobic Interactions in Coagulation. Journal of Colloid and Interface Science 132(2): 532-54.
10. Prestidge CA (2000) Rheological investigations of DLVO and non-DLVO particle interactions in concentrated mineral suspensions. Mineral Processing and Extractive Metallurgy Review 20(1): 57-74.
11. Barthelmez G, Pratsinis SE, Buggish H (2003) Particle size distributions and viscosity of suspensions undergoing shear-induced coagulation and fragmentation. Chemical Engineering 58(13): 2893-2902.