Analysis of Fly Ash and Paramagnetic Nanoparticles with Hybrid Base Fluid Due to Applied Magnetic Dipole in a Stretching Sheet with Momentum Slip Condition: FEM Approach

Ferrofluids (a portmanteau of liquid and ferromagnetic particles) are liquids in the presence of an external magnetic field magnetized. These types of fluids are liquids colloidal made by nanoscale ferromagnetic or ferromagnetic particles suspended in a fluid carrier (usually a water or organic solvent). The particle suspension is caused by Brownian movement and the particles do not settle under normal circumstances. In addition, each ferromagnetic particle is covered with a surfactant to prevent agglutination. Magnetic attraction of ferromagnetic particles at the nanoscale is low when the surfactant has sufficient strength to inhibit agglomeration or magnetic aggregation. There are various applications of ferromagnetic liquids. They are often used in many industrial applications, food preservation, aerodynamics, nuclear power plants, crystal processing, laser, avionics, robotics, coolant, semiconductor processing, fiber optics, speakers, cooling, filtration, plastic drawing, aerodynamics and computer peripherals, etc. Countless applications from many scientists and researchers have accelerated the study of ferrous fluid. Neuringer [1] investigated the effects of gradients of magnetic and thermal fields on saturated viscous ferrofluid flow. Crane [2] initiated the Newtonian fluid flow with a linear stretching sheet, which was then reduced to non-Newtonian fluids. Anderson and Valnes [3] investigated the special effects of the magnetic dipole on the ferrous liquid. Titus and Abraham [4] studied ferrofluid and heat transfer beyond an expandable sheet. Some research on ferrofluid is given in the references [5-11].

The rapid growth of engineering and technology, especially in the field of electronics, energy production and energy efficiency brings the need to develop different cooling techniques. Nano fluids, in this case as a new type of heat transfer fluid are recently a popular research area for researchers and the aims to overcome the disadvantages of poor thermal conductivity conventional heat transfer fluids by improving their thermal resistance conductivity using new methods [12]. Nanofluids are essentially fluids that contain particles with a high thermal conductivity, suspended in a basic fluid [13]. Mixed convection on MHD flow of casson nanofluid over a non-linearly permeable stretching sheet has been investigated and analyzed numerically by Ghadikolaei et al. [14]. Nor Azizah Yacob et al. [15] studied the characteristics on a forced convection boundary layer flow towards a horizontal permeable stretching sheet in four types of nanofluids which are ZnO-water, ZnO-Kerosene, MgO-water and MgO-Kerosene. Hussanan et al. [16] focused on the energy transfer with the effects of carbon nanotubes (CNTs) of magneto hydrodynamic (MHD) nanofluids flow past a stretching sheet under thermal radiation and Newtonian heating. Single and multi-wall CNTs are considered in water as convectional based fluid. Numerical simulation for mixed convective threedimensional slip flow of water-based nanofluids with temperature jump boundary condition is presented by Mahanthesh et al. [17]. Nanoparticle shapes on radiative MHD water based aluminum alloy nanoparticles, AA7072 and AA7075 flow up a non-linear wall with distinct flow condition is analyzed by Kandasamy et al. [18]. The unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid is studied by Waini et al. [19].

Microstructured fluids are called micro polar fluids. Micro flow fluids belong to a class of non-asymmetrical fluids stress tensor, called polar fluids. Micropolar fluid mechanics, de- rived from the theory developed by Eringen [20], is an interesting research area because of the wide range of applications in the industry. For example, polymeric liquids, actual liquids with suspensions, liquid crystals, animal blood, and exotic lubricants are modeled by micro polar fluids. In general, these fluids indicate fluids that cover unpredictably oriented fluids suspended in a viscous medium. In the book by Lukaszewicz [21], micro polar fluids are briefly studied. Many studies consider micro polar fluids, but those dealing with nanoparticles are limited. The suspension of nanoparticles will result in more complex nanofluids.

The thermo physical properties of the fly ash nanofluid are the main factors of influence of heat, friction and automotive cooling system energy performance. Thermo physical properties are thermal conductivity, density, dynamic viscosity and specific heat of base fluid Sozen et al. [22] reported that fly ash exhausted from thermal power plants has a mixture of metal oxides like Al2O3, Fe2O3, TiO2, SiO2, CaO and MgO in different proportions, which could be used for preparing nanofluids suitable for heat exchanger applications. They have proven that fly ash nanoparticles with water have improved thermo physical and friction properties with good improved thermal performance in a concentric parallel flow heat tube exchanger

Present work concentrates on the analysis of fly ash and paramagnetic ( T _a ) nanoparticles with hybrid base fluid (60% water, and 40% ethylene glycol) due to applied magnetic dipole on a boundary layer slip flow over a stretching sheet. The effect of ferrohydrodynamic interaction parameter, thermal radiation, viscous dissipation, micro polar parameter, and Prandtl number were studied. Computations of nonlinear system are presented after non dimensionalization using the finite element method. The comparison of finite element method with previous researches is tabled.

Considering a steady two-dimensional electrically nonconducting and the incompressible flow of magnetic micro polar nanofluid consists of paramagnetic ( T _a ) and fly ash nanoparticles suspended with a hybrid base fluid (60% water, and 40% ethylene glycol) over a stretching sheet. Partial velocity slip is considered at the surface and the suction/injection effect is also taken into account. The sheet is stretched along x axis with linear velocity uw = cx . Where c > 0 is for stretching and c < 0means shrinking of the sheet. The magnetic dipole of sufficient strength to fill the ferrofluid is located at a distance a below than the x-axis and it centers on the y-axis whose magnetic field in the positive x-direction. It is assumed that the Curie temperature c T is higher than the ambient temperature w T , while the free flow temperature is far from the surface of the stretching/shrinking sheet c T T ∞ = and therefore cannot magnetize until it begins to cool down after it has penetrated into the region of thermal boundary layer. We thus have [23, 24]

Where, m is a boundary constant parameter with 0 ≤ m ≤1 and A is the velocity slip factor. The flux of magnetic ferrofluid is affected by the magnetic field because the magnetic dipole with a magnetic scalar potential is expressed as

Since the magnetic force is equal to the slope of the magnitude of H . The resultant magnitude H of the magnetic field strength is expressed as:

The Roseland average absorption coefficient of is 1 K and the constant of Stefan Boltzmann isα * . If small temperature differences are taken into account during the inflow, higher order term are neglected using the Taylor series, we get

In view of similarity transformation Eq (14), the partial nonlinear differential Eqs (2)-(4) transform into the following system of nonlinear ODE’s:

Finite Element Method Solutions

The finite element method (FEM) is a powerful technique for solving differential or partial equations and integral equations. The basic concept is that the entire domain is divided into smaller finite-dimensional elements called finite elements. FEM is used to solve many problems in fluid mechanics [28-32]. To compute the solution of these equations, presume that

Variational formulations

Finite element formulations

The finite element model may be obtained from Eqs (23)-(27) by plugging the following finite element approximation form.

are supposed to be known. The system of equations obtained from Eq. (34) is of the order 10 × 10 and the whole flow domain is distributed into 1000 linear elements of same size. We obtain a matrix after assembly of all element equations. After the assembly of the system of equations of elements, a system of non-linear equations is obtained, therefore an iterative method is used for the solution. To compute f , h , the functions are supposed to be notorious at a lower iteration level to linearize the system. Subsequently, the estimates of velocity, solute, nanoliquid and temperature, volume fraction profile for a high level are fulfilled and continue until the desired accuracy of 0.00005 is achieved. To guarantee the independence of the mesh, the impact

capacity of the mesh has been implemented. There is no significant difference in the observed effects forξ >12 . For this reason, ξ is set to 12. To corroborate the convergence of the consequences, we wanted the amount of elements that increases n = 60, 100, 120, 240, 260, 48, 500, 700, 1000 and 1100, the results are delimited in Table 2. In addition, we have examined that, since n increases more than 1000, there is no significant alteration of the velocity, temperature, and concentration functions, so the results are reported for the elements n = 1000 (Table 2&3).

Results and Discussion

We intend to provide the numerical solution of resulting systems by finite element method. In this attempt the behavior of fly ash and paramagnetic nanoparticles and their thermal conductivity on boundary layer slip flow in the presence of magnetic dipole are investigated. Moreover, the core objective is to visualize the impact of various physical parameters like dimensionless ferromagnetic parameter β , micro polar parameter K , Prandtl number Pr , radiation Rd , viscous dissipationλ , and dimensionless Curie temperature ratio s on velocity, micro rotation and temperature profiles. Table 1 exhibits the physical and thermal properties of hybrid base fluid and nanoparticles (fly ash and paramagnetic ( ) a T ). For verification purposes, the results of this study have been compared with the results of other researchers [2,33,29,27,34] in Table 3-4. The effect of the ferromagnetic parameter β on dimensionless velocity and temperature is investigated in Figures 2 and 3 and showed that the velocity profile decreased and temperature profile increased with increasing ferromagnetic parameter. From a physical point of view, it is due to the fact that the increase in β develops the resistance forces in the fluid, which leads to a deviation from the Lorentz force that reduces the velocity. As expected larger estimation of ferromagnetic parameter enhances Lorentz force which gives resistance force and therefore thermal field enhances. It is noticed that the velocity boundary layer thickness for fly ash nanoparticles is much higher than that of paramagnetic ( θ₂ ) a T nanoparticles. Whereas, an opposite behavior is found for temperature profile. The thickness of the thermal boundary layer for a paramagnetic nanoparticles Ta has a maximum increase followed by fly ash nanoparticles in Figure 3. Figures 4 and 5 depict the influence of micro polar parameter (K) on velocity and temperature profiles in the presence of slip condition (A = 0.5). The micro-rotational parameter values show an increasing trend in velocity and micro-rotation profiles. The impact of slip condition shows that the velocity and micro-rotation boundary layers increases in the presence of slip condition (A = 0.5). The thermal diffusivity decreases when the Pr parameter is increased. The reduction in thermal diffusivity is responsible for the heat dispersed from the heated surface and, by the way, the temperature gradient on the surface is increasing. This phenomenon reduces the energy capacity which reduces the thickness of the thermal boundary layer and increases the axial velocity; the results are shown in Figure 6. And also, we observed that the temperature boundary layer thickness for paramagnetic nanoparticles is higher than fly ash nanoparticles. Figure 7 emphasizes the effect of the thermal radiation parameter Rd on the fluid temperature profile ( θ₂ ) 1 θ . Since, the temperature increases as the radiation upsurges. This can be accredited to the physical statistic according to which the thickness of the thermal boundary layer increases with the increase of the radiation parameter. The thermal field disintegrates for a larger estimate of the viscous dissipation parameterλ illustrated in Figure 8. Impact for a higher viscous dissipation parameter decreases the thermal conductivity of the liquid and consequently the thermal field decreases. The impact of viscous dissipationλ and Curie temperature s on the ferrofluid temperature profile ( θ₂ ) 2 θ are depicted in Figure 9 and 10. From the figures, we noticed that with increasing value of viscous dissipation and Curie temperature the ferrofluid temperature profiles enhanced.

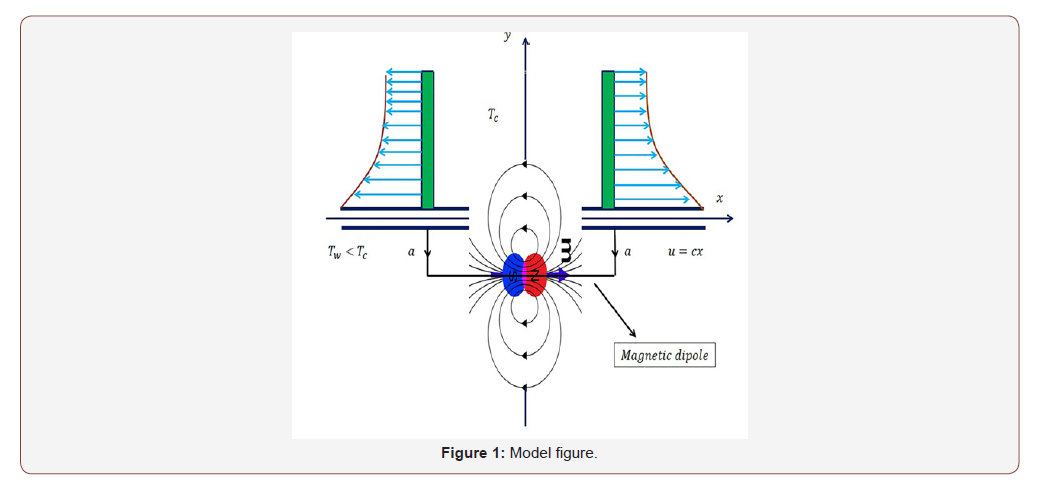
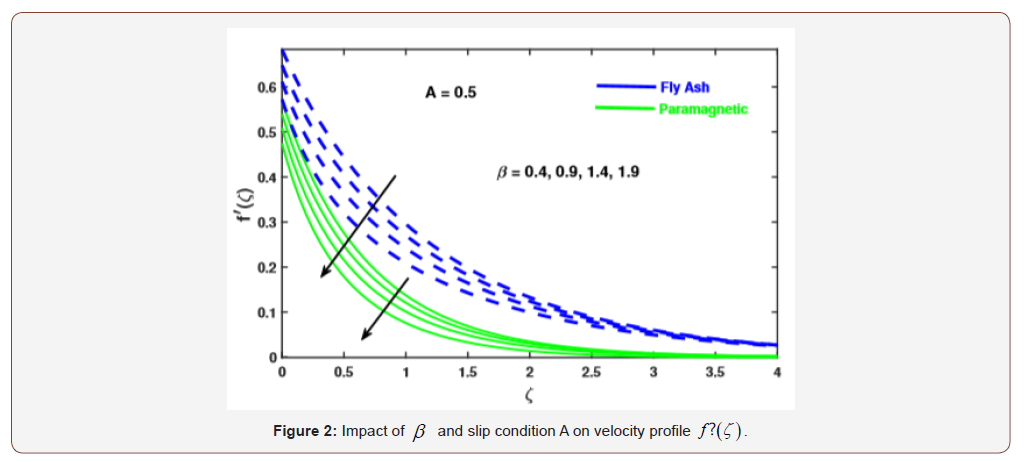
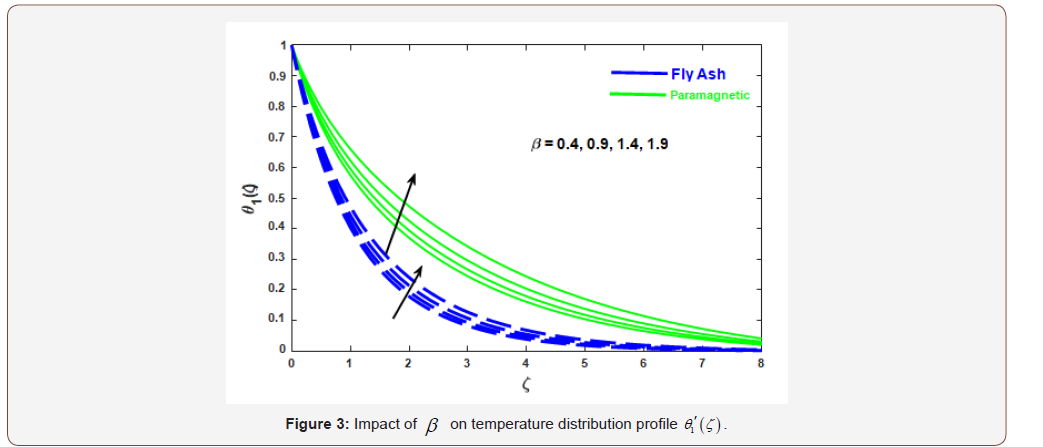
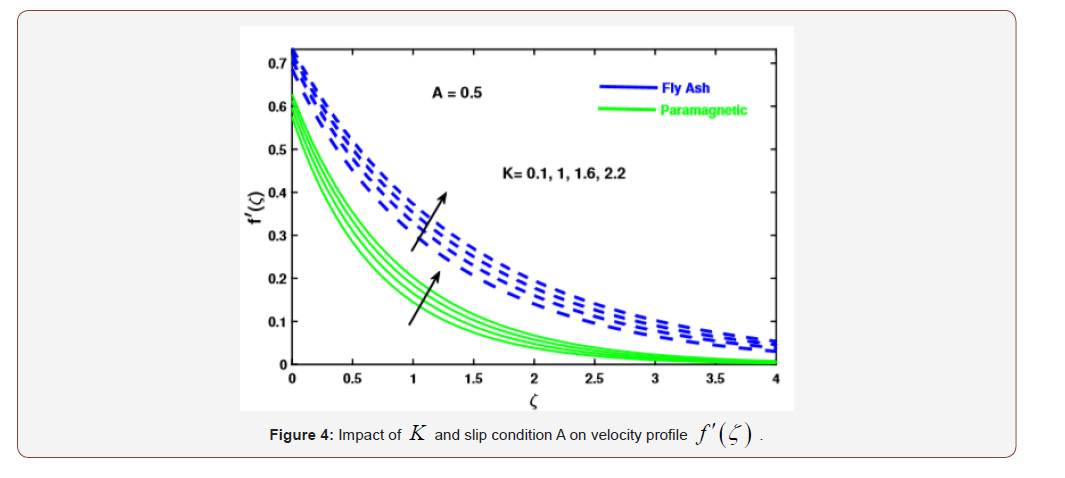
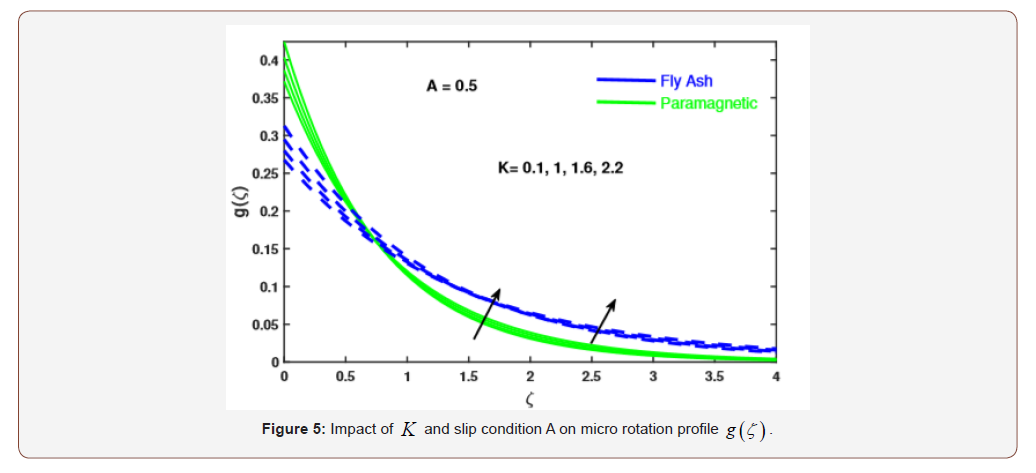
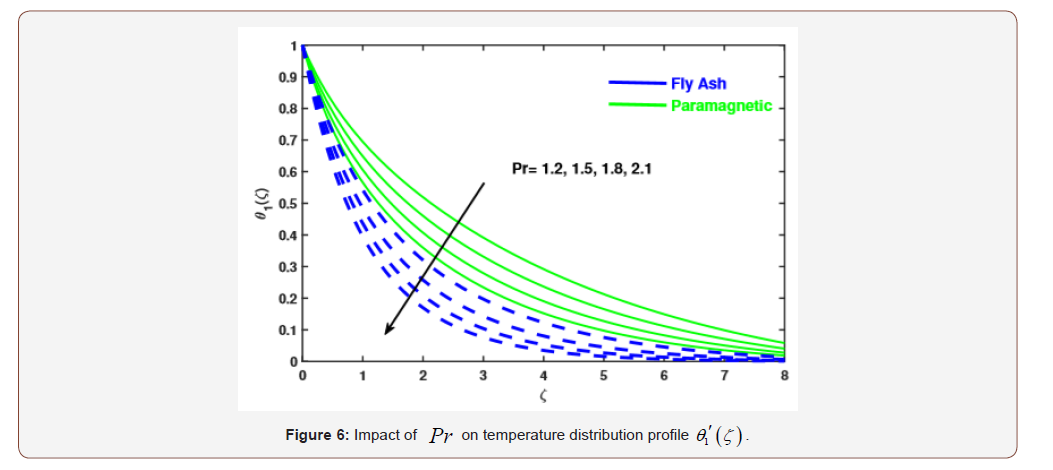
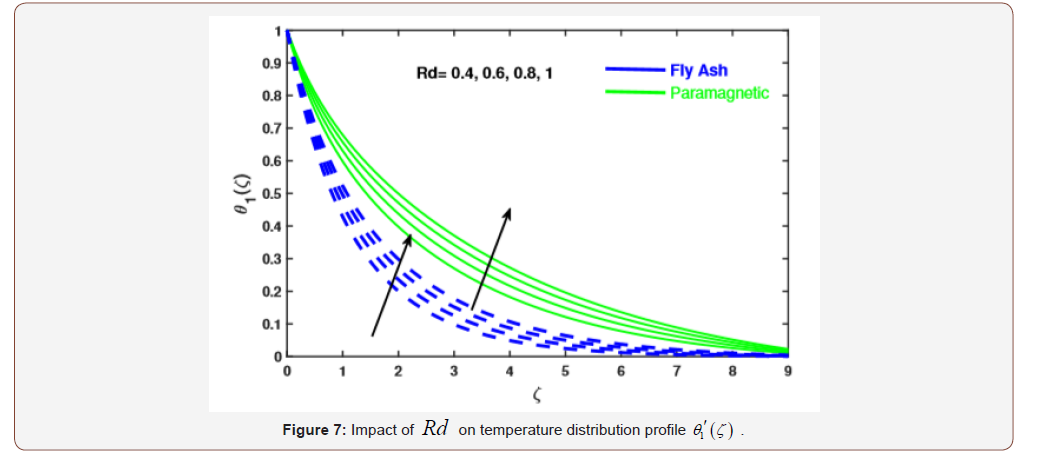
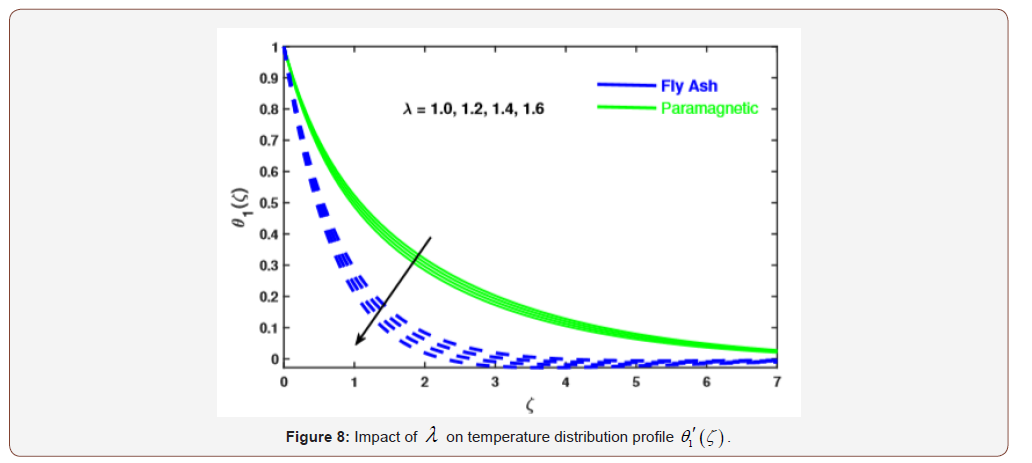
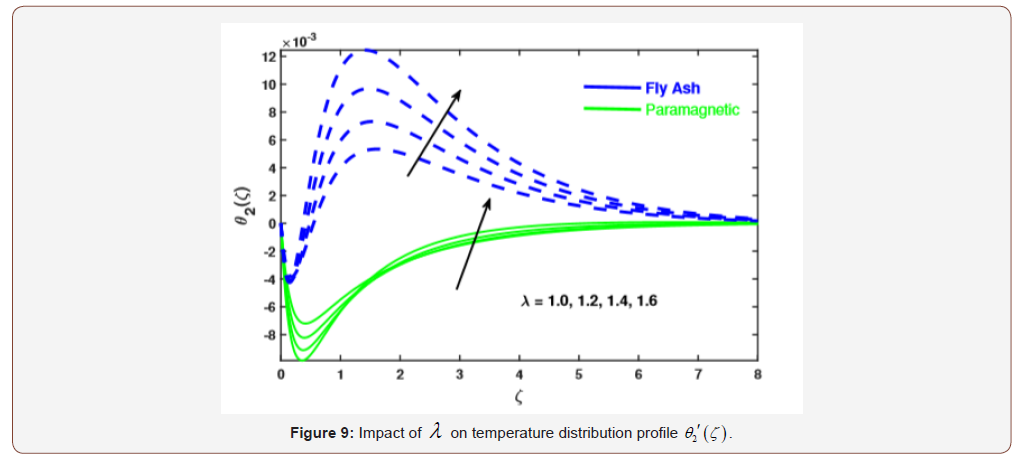
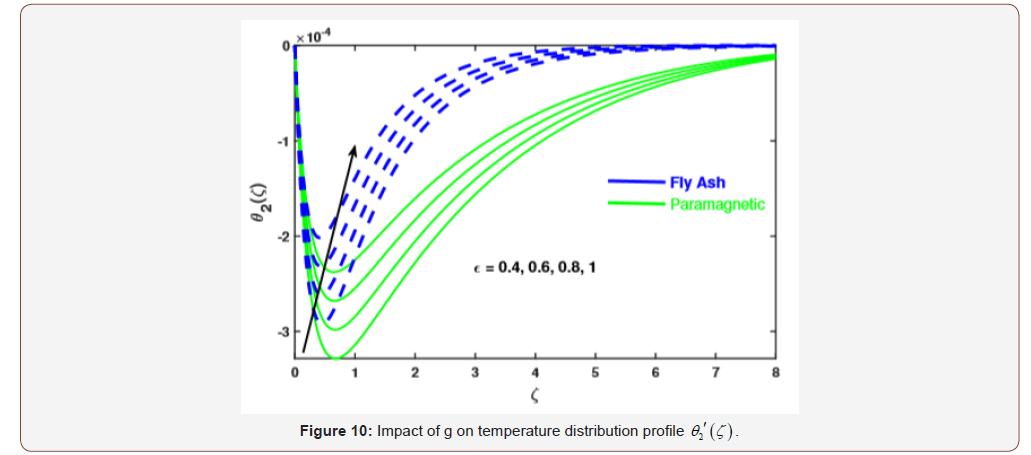
Table 1:Thermo physical properties of fly ash and paramagnetic nanoparticles with water fluid.

Table 2:FEM convergence results of h(ζ), g(ζ), θ1(ζ), and θ2(ζ) at the 3 of computational domain [0,10] for different number of elements when Pr = 2, K = 0.1, λ = 0.01, φ = 0.2, β = 0.5, g = 2, m = 0.5, fw = 0.2, Rd = 0.5

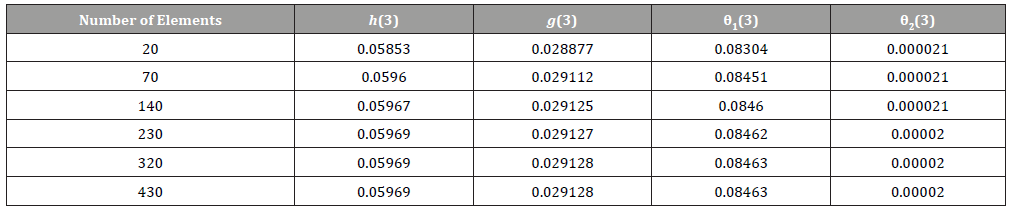
Table 3:Comparison of the exact solution of Crane [2] and FEM for the flow velocity f ˊ(η).

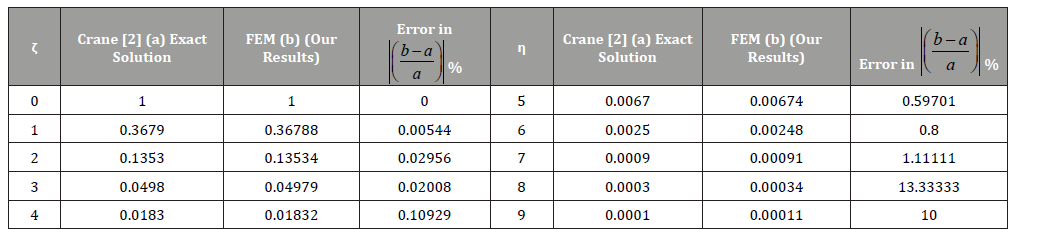
Table 4:Comparison of −θˊ(0) for various values of Pr and σ when all others parameters are zero.

Conclusion

In this study, analysis of fly ash and paramagnetic nanoparticles due to applied magnetic dipole over a stretching sheet with momentum slip condition are examined. Governing equations were solved by finite element method. The impact of relevant parameters on velocity, micro rotation velocity, and temperature are demonstrated graphically. Results revealed that.

• The velocity profile decreased and temperature profile increased with increasing ferromagnetic parameter (β ) , and also noted that the velocity boundary layer thickness for fly ash nanoparticles is much higher than that of paramagnetic ( Ta ) a T nanoparticles.

• The escalating values of K upsurges the micro rotation and velocity profile and with the presence of slip condition, the boundary layers of velocity and micro rotation profiles increases.

• The increasing values of Pr and λ reduces the temperature profile (θ₁) , while the escalating values of Rd increase θ₁ .

• The ferrofluid heat transfer rate (θ₂) escalates with enhancing the values of λ and s.

• From the above results, we noticed that the thermal boundary layers thickness for paramagnetic nanoparticles is much higher than fly ash nanoparticles.

Acknowledgement

None.

Conflict of Interest

No conflict of interest.

1. JL Neuringer (1966) Some viscous flows of a saturated ferro-fluid under the combined influence of thermal and magnetic field gradients. International Journal of Non-Linear Mechanics 1(2): 123-137.
2. LJ Crane (1970) Flow past a stretching plate. Journal of Applied Mathematics and Physics ZAMP 21(4): 645-647.
3. H Andersson, O Valnes (1998) Flow of a heated ferrofluid over a stretching sheet in the presence of a magnetic dipole. Acta Mechanica 128(1-2): 39-47.
4. LR Titus, A Abraham (2014) Heat transfer in ferrofluid flow over a stretching sheet with radiation. Int J Eng Res Tech 3(6): 2198-2203.
5. E Aursand, MA Gjennestad, KY Lervåg, H Lund (2016) A multi-phase ferrofluid flow model with equation of state for thermomagnetic pumping and heat transfer. Journal of Magnetism and Magnetic Materials 402: 8-19.
6. S Mojumder, KM Rabbi, S Saha, MN Hasan, SC Saha (2016) Magnetic field effect on natural convection and entropy generation in a half-moon shaped cavity with semi- circular bottom heater having different ferrofluid inside. Journal of Magnetism and Magnetic Materials 407: 412-424.
7. ED Vtulkina, EA Elfimova (2017) Thermodynamic and magnetic properties of ferroflu- ids in external uniform magnetic field. Journal of Magnetism and Magnetic Materials 431: 218-221.
8. Y Zhang, M Zhang, Y Bai (2017) Unsteady flow and heat transfer of power-law nanofluid thin film over a stretching sheet with variable magnetic field and power-law velocity slip effect. Journal of the Taiwan Institute of Chemical Engineers 70: 104-110.
9. M Hassan, A Zeeshan, A Majeed, R Ellahi (2017) Particle shape effects on ferrofuids flow and heat transfer under influence of low oscillating magnetic field. Journal of Magnetism and Magnetic Materials 443: 36-44.
10. M Ijaz, M Ayub (2019) Simulation of magnetic dipole and dual stratification in radiative flow of ferromagnetic maxwell fluid. Heliyon 5(4): e01465.
11. N Muhammad, Nadeem, M (2019) Impact of magnetic dipole on a thermally stratified ferrofluid past a stretchable surface. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 233(2): 177-183.
12. JR Babu, KK Kumar, SS Rao (2017) State-of-art review on hybrid nanofluids. Renew- able and Sustainable Energy Reviews 77: 551-565.
13. M Corcione (2011) Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids. Energy Conversion and Management 52(1): 789-793.
14. S Ghadikolaei, K Hosseinzadeh, D Ganji, B Jafari (2018) Nonlinear thermal radiation effect on magneto Casson nanofluid flow with joule heating effect over an inclined porous stretching sheet. Case Studies in Thermal Engineering 12: 176-187.
15. NA Yacob, A Dasman, S Ahmad, NF Dzulkifli (2018) Numerical solutions of forced convection boundary layer flow towards a horizontal permeable stretching sheet in ZnO–water, ZnO –kerosene, MgO–water and MgO –kerosene nanofluids. in: Regional Conference on Science, Technology and Social Sciences (RCSTSS 2016), Springer, pp. 917-927.
16. A Hussanan, I Khan, MR Gorji, WA Khan (2019) CNTs-water–based nanofluid over a stretching sheet. BioNanoScience 9 (1): 21-29.
17. B Mahanthesh, B Gireesha, RS Gorla, OD Makinde (2018) Magnetohydrodynamic three-dimensional flow of nanofluids with slip and thermal radiation over a nonlin- ear stretching sheet: a numerical study. Neural Computing and Applications 30(5): 1557-1567.
18. R Kandasamy, NA Bt Adnan, JAA Abbood, M Kamarulzaki, M Saifullah (2019) Electric field strength on water based aluminum alloys nanofluids flow up a non- linear inclined sheet. Engineering Science and Technology, an International Journal 22(1): 229-236.
19. I Waini, A Ishak, I Pop (2019) Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. International Journal of Heat and Mass Transfer 136: 288-297.
20. AC Eringen (1966) Theory of micropolar fluids. Journal of Mathematics and Mechanics pp. 1-18.
21. G Lukaszewicz (1999) Micropolar fluids: theory and applications. Springer Science & Business Media.
22. A Sözen, HI Variyenli, MB Özdemir, M Gürü, I Aytaç (2016) Heat transfer enhancement using alumina and fly ash nanofluids in parallel and cross-flow concentric tube heat exchangers. Journal of the Energy Institute 89(3): 414-424.
23. T Hayat, S Ahmad, MI Khan, A Alsaedi (2018) Exploring magnetic dipole contribution on radiative flow of ferromagnetic williamson fluid. Results in physics 8: 545-551.
24. M Waqas (2020) A mathematical and computational framework for heat transfer analysis of ferromagnetic non-newtonian liquid subjected to heterogeneous and homogeneous reactions. Journal of Magnetism and Magnetic Materials 493: 165646.
25. B Palaniappan, V Ramasamy (2019) Thermodynamic analysis of fly ash nanofluid for automobile (heavy vehicle) radiators. Journal of Thermal Analysis and Calorimetry 136(1): 223-233.
26. A Majeed, A Zeeshan, T Hayat (2019) Analysis of magnetic properties of nanoparticles due to applied magnetic dipole in aqueous medium with momentum slip condition. Neural Computing and Applications 31(1): 189-197.
27. A Majeed, A Zeeshan, R Ellahi (2016) Unsteady ferromagnetic liquid flow and heat transfer analysis over a stretching sheet with the effect of dipole and prescribed heat flux. Journal of Molecular Liquids 223: 528-533.
28. SA Khan, Y Nie, B Ali (2019) Multiple slip effects on magnetohydrodynamic axisymmetric buoyant nanofluid flow above a stretching sheet with radiation and chemical reaction. Symmetry 11(9): 1171.
29. B Ali, Y Nie, SA Khan, MT Sadiq, M Tariq (2019) Finite element simulation of multiple slip effects on MHD unsteady maxwell nanofluid flow over a permeable stretching sheet with radiation and thermo-diffusion in the presence of chemical reaction. Pro- cesses 7(9): 628.
30. M Sheikholeslami (2019) New computational approach for exergy and entropy analysis of nanofluid under the impact of lorentz force through a porous media. Computer Methods in Applied Mechanics and Engineering 344: 319-333.
31. M Hamid, M Usman, Z Khan, R Haq, W Wang (2019) Heat transfer and flow analysis of casson fluid enclosed in a partially heated trapezoidal cavity. International Communications in Heat and Mass Transfer 108: 104284.
32. SA Khan, Y Nie, B Ali (2020) Multiple slip effects on mhd unsteady viscoelastic nanofluid flow over a permeable stretching sheet with radiation using the finite element method. SN Applied Sciences 2(1): 66.
33. ME Ali (1994) Heat transfer characteristics of a continuous stretching surface. Heat and mass transfer volume 29(4): 227-234.
34. N Bachok, A Ishak, R Nazar (2011) Flow and heat transfer over an unsteady stretching sheet in a micropolar fluid. Meccanica 46(5): 935-942.