Worldwide Shameful Violation of the Energy Law from 1992 Till Now by Academy and Industry

Academic Sciences and Physics accepted since 1992 [1] a new analysis of force vs depth analysis of (nano) indentations on the basis of a normal parabola (force versus depth²), which violated the energy law (work equals energy) and did not agree with the experimental exponent of the load vs depth exponent. And the DIN-ISO-NIST-14577standard, which is an enforcing part of the admission for Instrument builders agreed with that. It was highly acclaimed to the responding Academia and all trials of the present chemist who started in 1995 with nanoindentations, when he and his co-workers (as summarized in [2]) could not reproduce the h² and thus questioned the correctness of the exponent 2 empirically. The physical proof and the energetic questions of the phase transitions under load could not be applied for, as the support of granting Reviewers was completely missing for such a presumably extremely complicated task, in view of the DIN-ISO-NIST-14577 standard, that physicists had not resolved. It was either told that this discrepancy would apparently exist only in the hands of chemists, or that they indented onto inadequate materials. It did not help that physicists could not reproduce their own experimental results with h², which was deduced within the complicated series of formulas from the elasticity theory. They used instead 3 +8 free-parameter iterations by using h² without checking the exponent of the experimental loading curves. That was with respect to the unsuitable (then unchecked twinning) standards fused quartz or aluminium. Such behavior is unscientific and far away from good scientific practice GSP). Even worse, the “simplification” in [1] did (also?) not respect the energy-law. Another approach is simulations on the basis of the false exponent and again not obeying to the energy law that of coarse leads to parabolas with exponent 2 and can so be recognized as unphysical. The present author is an organic chemist and he could at first only empirically collect hundreds of own and published loading curves for all types of solid materials, including the Handbook of his instrument, that are collected in [3]. He always confirmed h^3/2 but neither h² nor broken exponents between 3/2 and 2. All experimental loading parabolas analyzed with exponent 3/2 on h and numerous of them indicated phase transition and materials very sharply at their typical force. That is the most important subject of nanoindentation and it was published and presented at numerous international conferences. But physicists remarked over and over again that the physical proof was missing. But the unbelievable insanely complicated deduction sequences for decades (so-called Hertz theory), as derived from elasticity theory (that were the physical basis for exponent 2 and could not give the correct solution, because the obvious containing disregard of the energy-law must be hidden somewhere therein. Thus, the chemist (why not the physicists?) was initially misled from finding the actually very simple physical proofs. He dreamed them and immediately wrote them down upon wake-up, by just reminding his mathematic and physical school courses at his ages of 14 -16 years. The first detection was the severe energy-law violation (when comparing the applied work with the indentation work from the loading curve) as published in [4] and [5] and then the exponent 3/2 foundation (by use of the indenter geometry) [6]. And he found at sufficient loading force characteristic phase-transition kinks under appropriate loads in F_N vs h^3/2 plots, what is typical for most materials at materials- dependent loading size. Such important phase transitions under mechanical load can never be detected with the unphysical exponent 2 on h. Nevertheless it became more and more difficult to publish the correct indentation results, because renowned scientists who made their career with the false result, as derived from the elasticity theory, the publication of [7] 2014 and the DIN-ISONIST- 14577 looked for excuses and still fought against the physical mathematical reality. At first, the rejected break-through publication at the journal Scanning of [4] in 2013 could only be published when I convinced the Editor that his “Peer Reviewer” had used an important part of it without citation in his following own publication in Scanning. I did not use names, but used only the term “your Reviewer”, so that this miserable situation could be silently and immediately be settled by publication of my work [4]. And I published the energetic law violation elsewhere [5].

It is very clear that the indentation loading curves (force F_N against depth h) form parabolas. The very basic math courses (for pupils at ages 14-16) treat only the “normal parabola” with exponent 2 (F_N =h²), but not with parabolas with different exponents (e. g. 3, 4, or 3/2, etc). Thus, the physically highly trained Authors of [1] knew only the normal parabola and they could define a hardness value H as force over area containing h². That was unphysical adapted for H_ISO in the DIN-ISO-NIST-14577 standard. It falsely uses the complete applied normal force /projected circle or triangle area with a dimension [N/m²] for the calculated hardness HDIN-ISONIST from the squared maximal depth and projected area, but they forgot about the various sidewise events (pressure and its actions).

The fight against the correct instrumental indentations have been very biased, because all collected “Peer-Reviewers” were biased or tried to protect themselves, because it must certainly be shameful for being part of believing into energy-law violation and not considering the geometry of the indenter, not to speak of their dichotomy [8].

There was a long series of Troyon’s claim of broken and changing exponents [9]. Their broken exponents for fused quartz varied from 1.64533, to 1.82723, over 1.5, to 1.75285. Such changing broken exponents are of course in error and useless. They derive from the fact, that they include the various initial errors, because they depend on the material’s surface and any contact finding errors of the operator. And they include tip rounding and different effects and must be discarded. But they are generally corrected by the axis- cut. Unfortunately, Troyon et al falsely tried to blame the present author with their Figures 1 and 2 (similarly 13 and14 with copper) and with ridiculous lines through two of the initial points that must be discarded. One should have drawn the first linear branch of the F_N vs h^3/2 plot for creating the phase-transition kink. Also an exponent of 1.64903 was published for steel by using their initial error. The correct analysis of experimental loading curves from the Troyon group [9] follow h^3/2, while their finite Element simulated ones follow h², which is quite remarkable and questionable.

Even worse is the trickery by the Durst group [10]. They draw in their figure 3b a normal parabola (FN = h²) and used my technique for proving its exponent 2 by plotting their figure 3b for obtaining a straight line. That is the proof that the normal parabola by them has indeed the exponent 2, which is everywhere taught in mathematic courses. But they falsely call it “usual old, P-h² fit” (instead of exponent analysis). And they continued asking “[7] to d and [3] to c” in their figure 3, for showing what they termed “Double P-h_3/2 fit after Kaupp et al., (their reference15)”. What a misleading trial? The normal parabola has exponent 2 and that can of course not be analyzed with the exponent 3/2 on h. Kaupp et al analyse the parabolas of conical and pyramidal indentations and these follow not the normal parabolas with exponent 2, but mathematical correct as F_N vs h^3/2 parabolas (see next Section), and there is no “fitting” whatsoever. The reports of loading curves of fused silica, sapphire, ufg-Al and cg-Al are reported with exponents 1.94, 1.97, 1.88 and 1.88 all with “fit-quality” of 0.999 for the whole loading curve in [10] but it is not told whether that is their figure 1a (up to 800 mN) or 1b (up to 30 mN). And it is not told which crystallographic faces were indented, for clarifying these claims. The confidences of h_3/2 analyses are at least 0.9999, when all of the hundreds of experimental points are available. As it is known from other publications that these materials undergo phase-transition under their characteristic loads (as revealed with exponent 3/2 instead of (here as almost 2), these values should be reinvestigated. We cannot accept that this report is close to exponent 2 in view of the easily detected phase-transitions (for fused quartz and aluminium, which are twinned under load [11].

In the introduction of [7] Merle et al cited 13 papers of different renowned authors, who should have theoretically and practically (including “Finite Element simulations”) served as witnesses “by having proved” the [unphysical!] “P-h² dependence” for “nanoindentations” with a pyramidal or conical indenter”. I do not repeat the names of such Celebrities. But all of these did not use the indenter geometry that determines the exponent on the depth h. And neither so avoided these Authors their violation of the energy-law (by the inevitable creation of the sidewise work for pressure that does not occur with zero energy). And also their quacking so-called “deduction” used the so defined indentation hardness as so -called “proof” of the exponent 2 for the indentation parabola. But that is doubly false in all of these cases: At first the exponent 2 for the depth must be replaced by 3/2, due to the geometry of the indenter. Second, nobody must violate the energy-law, but all of the applied force and thus energy is used in such standards.

We come now to the amount of work that has been agreed, to be obtained with zero energy. These physically highly trained Followers of [1] and DIN-ISO-NIST 14577 had apparently never tried any wood-cutting with a hatchet or an axe. That is regrettable, because they would have easily seen and experienced that they did not only put vertical energy for coming down vertically into the log but one also needs energy for the separating in parts due to intermediate sidewise pressure. If these highly trained Researchers set the horizontal energy part to zero they violate the energy law. Wood-cutting is not principally different from indentation. That is most easily mathematically analyzed [5]: Draw the parabola with h² together with the load triangle from zero to F_Nmax and h_max. Then compare the energy under the straight line W_applied= 0.5 F_Nmax h_max with the area under the normal parabola and see the energy-law violation, as the sidewise effects cannot occur with zero energy. Or just ask: why is there a free area between the parabola and its secant?

Another strange but highly applauded publication [12] even claimed that one should only rely of the late parts of the loading h² parabola when it (as all parabolas do) approaches linearity in accordance with [1] and the rest of the world. But that is a ridiculous affront: the depth values would increase enormously when choosing h² instead of h^3/2 for obeying to DIN-ISO-NIST-14577 standard!

The research group of the present author was supported by scientific-project applications that had to be formulated for being granted by reviewers of the grantee (Deutsche Forschungsgemeinschaft So all of our numerous publications with the coworkers (summed up with all named coauthors as cited in 2012 [2]). These could only try to empirically find out the empiric consistency that the always describing historical and standardized exponent 2 on conical or pyramidal instrumented indentation loading curves must be described by F_N = k h^3/2. Only the independence from granting after the present Author’s retirement could allow for switching to “Good Scientific Practice” (GSP) on the basis of undeniable physical-mathematical deductions. All of these publications with respect to indentations since 2013 are open access without any financial support, as a Scientist’s tribute of responsibility also after retirement. It is found in my given Internet domain, which includes also the earlier empirical publications. This was however multiply opposed with dichotomy [8], as shown in the Introduction. Only my retirement allowed for successful independent search for proving their unbelievable physical falsity with easy physical principles and mathematics. These applications could not claim that the overcomplicated indentation rules are unphysical. The necessary corrections of the world-wide accepted false analyses of the nanoindentation loading curves enforces us to repeat the deduction of the loading curves for conical and pyramidal instrumental indentations they are not commonly recognized, despite the widespread dichotomy [8] when authors obviously knew that their published loading curves follow F_N = k h^3/2, but used “F_N = k h/2” instead for worldwide publishing false standard hardness HDIN-ISO-NIST-14577 values with 3+8 parameter iterations or elsewhere started FE-simulations with h². And the worldwide disregard of h^3/2 due to aggressive unsuitable fights with the various false techniques, which are all disproved in the Introduction, require that I as authorized author must now respond with repetition of the unchanged complete published deduction text and formulas of [6].

Before the proofs for the exponent 3/2 for the conical and pyramidal indentation and the energy-law violation of DIN-ISONIST- 14577 a repetition must tell some trivialities with parabolas. They have the form y = k hⁿ (n=2 for the normal parabola). The “a” in the formula is responsible for the size of y/k pairs and n for the curvature with the dimension [N/hn]. For the unphysical DIN-ISONIST- 14577 standard it would read [force/depth²] that looks at first glance reasonable for people who in fact violate the energy law. However, for people who take care of the never questionable law work = energy, it has the dimension [mN/μm^3/2], which is the physical hardness of the indented material due to the separate vertical and sidewise forces of cones or pyramids. That is so trivial but all worlds opposed against it, so that we must repeat here the present author’s physical deductions that were only with highest troubles due to Peer Reviewers finally published. The energy violation correction 2013 and the correct exponent 2016 (submitted 2013, as delayed with several at Peer-Reviews and also with long delayed responses to rebuttals and not published until 2016). Clearly, our long-known empiric laws became now never questionable physical laws. But the physicists and technologists of DIN in 2024 enforced a vote against elemental calculation rules that could not be avoided by the petitioning Scientist. The vote was all against one for the DIN belief against mathematics: Upon the petition of the present Author they responded: “We know better than an academic Scientist how the indentation instruments must be build and controlled”. The petition was thus shut down and the Petitioner had to leave the room for the examination session for the examination of DINISO- NIST-14577. It did not help that the Petitioner argued that their renewed standard 14577 would so certainly not be agreed by NIST, because of 3 fatal crashes airliners that would have been avoided with a physically correct standard and was followed by the grounding of 280 airliners from that fleet for 18 months, by agreeing with the Petitioner’s publications. And also, that a famous historical vote in 1633 of the Roman Pope Urban VIII against the calculation rules of Galileo had also their disastrous consequences. It took close to 5 centuries for the regrettably agreeing with the primate of science over belief by the Roman Pope John Paul II on December 12, 2016. We can be faster!

The indentation couples two processes that must be differentiated, because the applied force must serve both of them. The production of volume is thus attributed to the fraction F_NV^m for vertical indentation. The production of sidewise pressure + loss of pressure (including plasticizing via pressure) to the displaced material is attributed to the fraction F_Npⁿ for pressure. As the multiplication of both factors must give the product F_N, these fractional forces must have exponents m and n<1, so that we obtain Equation (1).

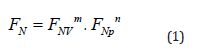
For the determination of the exponents m and n, we use the total pressure that could be reached at the depth h for absence of plasticizing. It is (p + loss of p) and we call it p_total . Equation (2) is evident, and the mathematical expression for a cone is V>_cone.

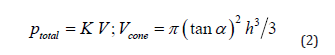
Equation (2) ptotal reveals that p_total and thus also F_Np are proportional to h³ of the immersed cone. Formula (3) is thus obtained for cones and pyramids (with effective “effective cone angles” ∝ )

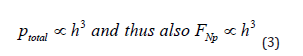
Formula (3) reveals the F_NP^1/3 proportionality to the depth h, but F_p^1/3 does not contribute to the depth. Nevertheless, when n = 1/3, m must be 2/3 according to Equation (1), and this gives Equation (4).

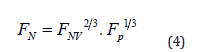
The exponent 2/3 on F_NV in Equation (4) reveals that while the instrumental indentation applies F_N, only the fraction F_NV^2/3 is responsible for the penetration and its depth h. This is expressed with the searched for Equation (5), where we do no longer need the index V.

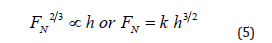
The unavoidable pressure/plasticizing factor F_Np^1/3 is lost for the depth. This is the physical reason for cones and pyramids (including Berkovich with some unavoidable wedge).

This deduction cannot be and has never been disproved, and F_N = k h^3/2 is thus a physical law.

The deduction of Equation (5) implies that DIN-ISO-NIST- 14577violates the energy law with pointed indentations, by claiming that the sidewise forces would falsely be created with “zero energy”, which is the most severe violation of the energy-law. They use falsely the complete measured normal-force F_N and thus they also severely violate the energy-law with their enforcing indentation- hardness definition (F_N / h²) with dimension [N/m²]. The error is both with the energy-law and according to eq. (5) also with the exponent. A false only believed exponent 2 would lose 1/3 of the applied energy upon indentation. But that remains always uncorrected. Conversely, the physically correct exponent 3/2 loses 1/5 of the applied energy. The physical indentation-hardness is thus always corrected by the present author with F_Nindent = (0.8 F_Napplied / h^3/2) with dimension [N/m^3/2]. This correct physical hardness definition might at first glance appear strange, but we deal here with indentation hardness and the geometries of the indenters require their urgent consideration as in eq (2). The latter had earlier been disregarded, but it must urgently be respected. We therefore remove here all historical errors that are still worldwide believed. Thus the worldwide believed “HDIN-ISO-NIST-14577” -values (force/ depth square) a disastrous: They are deduced from energy-law violation and false exponent by not considering the indenter geometry, leaving no chance for detecting phase-transitions under load producing micro-cracks at the polymorph interfaces as starting points of crashes, if their mechanical onset forces become superseded and led already to three fatal airliner crashings that could have been avoided, as discussed in the Conclusions.

In fact, DIN-ISO-NIST-14577 uses the complete applied force and thus energy of the penetration depth for their “hardness” definition as (force /depth²). They do so for making such uncorrected penetration depth value a determining factor for it. Such behavior is thus strongly physically burdened by the result from such energy- law violation.

The violation amount of “work with such zero energy, which is unimpressed still claimed, has been longer revealed and it appeared in [4] and [5]. Once more: the difference of the continuously increased loading energy triangle area from zero to F_Nmax with the area under the normal parabola shows that 1/3 of the applied work is lost for a believed h² penetration. The respective work is thus used for all non-penetrating sidewise work, when the exponent on h is believed to be 2. Thus, DIN-ISO-NIST-14577 violates the energy law with their unphysical exponent 2, by using all of the applied energy, in addition to their also use of the false exponent 2 on h. But 1/3 of it is so claimed occurring with zero energy. That is an extremely obvious violation of the energy law!

For the correct exponent 3/2 on h, the corresponding energy loss amounts to 1/5 of the applied energy. This is physically correct for the exponent 3/2 on h for the pointed indentation. That is illustrated with the simulated parabola of Wang et al [13] in Figure 1 (from their figure 3a in [13]), where 1/3 of the energy is claimed to be produced with zero energy. Clearly, all applied energy must be hold, when used for the published penetration depth. We exemplify that with a copy of their simulated curve, giving “FN = const h²” of gold, where the used triangle minus parabola area proves that the simulation was indeed started with the unphysical “h²”.

severe “data constructs” with loading parabolas give of coarse a linear plot with F_N ∝ h² as they belief in(or know only) an F_N = k h² normal parabola in view of the worldwide acclaimed and enforced indentation definition of the indentation- hardness H of DIN-ISO-NIST force / area (it is formulated by DIN (Deutsche Industrie Norm). But these and all followers forgot to include the shape of the indenters with their side-faces. And the dimension of Hphys is [N/m3/2] for pointed indentations, see (5). So all such H-values worldwide have to be replaced by physical indentation hardness for avoiding energy-law violation and false exponent hardness, which is, of coarse an epochal change, for no longer staying on an unphysical basis. That worldwide error leads to inexcusably and more than irresponsible risks of technical materials’ safety. Experimentally, gold also indents not with h², but with an F_N = k h^3/2 parabola linear F_N vs h^3/2 plot with characteristic kinks by twinning to higher forces etc [11]. Its energy loss by sidewise energy that is thus not 1/3 (from h²) as in Figure 1, but it must be 1/5 for the correct parabola. Correspondingly, a physically correct simulation would have provided linear F_N vs h^3/2 plots and their energy loss between secant and parabola would have precisely been 20%. But the simulation used h².

We used the secant in Figure 1 here only for visualizing the data- construct with the 1/3 loss of energy for a physically false indentation parabola exponents’ area between the secant and the parabola. That is the impossible 1/3 of the vertical force and thus energy, which is not valid for physical indentation parabolas and proves the use of the false exponent 2.

We see from Figure 1 that the simulation used the unphysical h² for the finite element parable simulation and that all further simulations should respect the physical reality. We stress here that already in 2008 existed the safe empirical basis of the correct exponent 3/2 on h but not 2. That was known to be valid for all several hundreds’ materials from very different material’s types. The linearized indentation parabolas existed [6] and 20% of sidewise energy was only by the present author used as loss for the sidewise applied work (instead of by creating it with zero energy). Thus, his calculations starting with the linear F_N vs h^3/2 plots used always F_Nindentation = 0.8 F_Napplication, for avoidance of an energy law violation, which corrected all of the force and energy values before of their exponential calculations. Thus, the indentation work is 0.8 times the applied work, and the energy law is not violated as we use in all consecutive calculations the indentation work (Wind = 0.8 W_applied). That is for example essential for the calculation of the phase transition energies in [3,11,14- 18] after their detection as sharp kinks of the F_N vs h^3/2 plots for the detection of their appearance force when using the physical exponent 3/2. For detecting of the force for phase-transition kink (the physical hardness is the penetration resistance k, mostly in [mN/μm^3/2] units from the F_N vs h^3/2 plots.

Phase-transitions increase the risks for micro-cracks along the interface between polymorphs and that is of utmost importance for the safety of mechanically stressed materials. An example is the micro- indentation of sodium chloride [18], as shown in Figure 2.

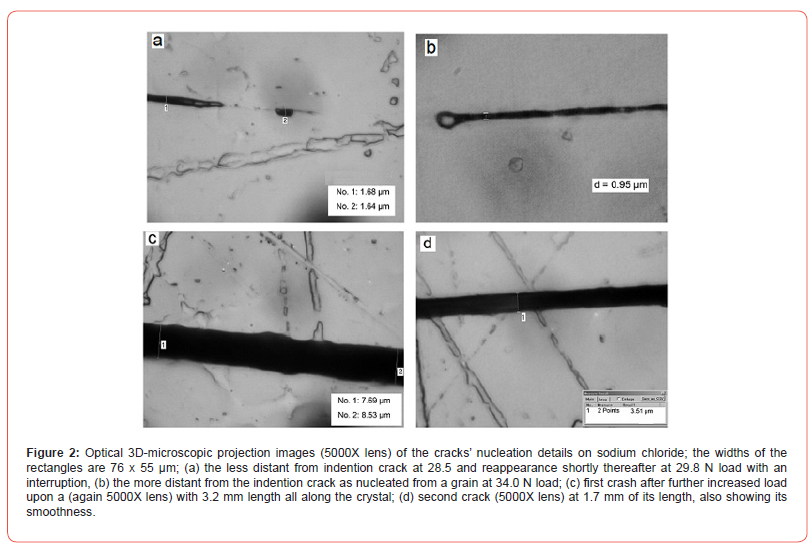
A very important drawback of the unphysical exponent 2 is its inability to detect phase transitions under load. Only the correct exponent 3/2 on h detects dangerous phase-transitions with their onset forces and energies. Cleary, different polymorphs of a solid material have different properties (here different physical hardness k, mostly in mN/μm3/2 units), which leads at the materials’ characteristic onset force with a sharp kink (it can never be seen when the incorrect “h²” is used). Its detection is most easy in F_N vs h^3/2 plots. One obtains up to shortly before the kink the highest possible concentration and purity of the unchanged material and at the following end or in case of a second kink shortly before it of the first polymorph etc. These are the best possible sites for structure determinations with the already available local X-ray, Raman, etc spectroscopy, which opens new possibilities for crystallography. That is unbeatably easy and cheap in comparison with anvil pressurisation (that provides no local concentration) and it will become the most important application of nano- or instrumental micro-indentation. But DIN-ISO-NIST-14577 standards must be urgently corrected for clearly most important safety reasons.

It is more than strange that there was not a single mathematician or math-teacher who discussed the trivial properties of parabolas with the developers of nanoindentation analyses. They started with high-principled elasticity theory and led to continued series of highest mathematics, which at perhaps certain points provoked simplifications that disregarded physical reality. The formulas even included relativistic features, so that only highly trained mathematicians will be able to locate such sites. But why should they have done that, because parabolas’ mathematical and physical and technical properties are so trivial that all physicists and technicians should have learned it in school. Thus it needed a chemist, who always has to completely understand and check what he does, to avoid any harm to what he does. He thus used the trivialities of a parabola and calculation rules with mathematical curve analysis and analysis of them. Unfortunately his undeniable result reveals the shameful (not only painful) errors of energy-law violation and of false exponent. These have been hidden in 3 + 8 free parameter iterations with black-box computers for the actual creation of what they want: hardness as force over area also in pointed indentations. Their loss in reputation is, of coarse very severe. Therefore the unsuitably repeated trials of fights again and against the physical truth found the highest acclamation. These could be published despite their obvious errors, as shown in the preceding Section.

However, the most important novelty of the physically correct analysis of loading curves, was the detection of sharp phase-transition( s) events under load in the analytical F_N vs h^3/2 plots as sharp kinks (rather than the therefore unsuitable logarithmic plots). As polymorphs of solid materials have generally different indentation hardness, these phase-transitions create sharp characteristic kinks at precise onset-forces and h^3/2 values. This is the easiest way for the detection of phase transitions under load and unless other techniques. One finds these easier and better than by the very expensive and difficult anvil pressurizing that can not concentrate. One has now the onset-pressure value and can even arithmetically calculate the phase-transition energy [14-18]. And if one wants to know the crystal structure of the polymorph, one can choose the highest concentration of the polymorph in question for the local determination techniques, which became very recently available. These are at the indentation end, or in case of consecutive phase-transitions close to the next kink. Such equipment should now be made available and it opens up a new field for crystallography.

Most importantly, the now easily detected phase-transitions under load are very dangerous, if these occur with materials that are exposed to sometimes very high forces. Examples are turbulences at the pickle forks of airliners (where the wings are connected to the trunk), or turbines, or the wings of air mills, or bridges- or balconies, or earthquakes, etc., etc.

It had been shown with instrumented Berkovich micro-indentation, that 1-2 μm long persistent (for more than 6 months) nano cracks in dry NaCl occurred upon the obtained phase-transition kink at 30 N load. That phase-transition was saved and later imaged under a digital microscope (5000-fold) [18], which showed the formation and development of micro-cracks (initially 1-2 μm long). Thus, any phase-transitions under load enhance the probability for such events and these can grow. Such stable local micro-cracks can trigger fatal cracking when their material becomes exposed to (usually much) higher possible forces. These are efficient starting points along them, which had been imaged with warnings discussed in [18]. In [18] that crashing required higher forces and a triggering by the micro-cracks is more than likely. If the applied indentation force was further increased (here above 50 N load), the whole material developed a full crash along from and in the direction of the micro-crack. The saved data were imaged next day and six months later viewed (when kept under exclusion of moisture) under a digital microscope, and published [18] with the corresponding warnings from phase transitions. It took 4 years until acceptance because it was repeatedly rejected with always extremely long times for Peer Reviews and Rebuttals at the US journal Scanning and then also the same at the Swiss journal Crystals. Here the second rejection was next day, because [7] had quacking deduced that the “ISO-14577 hardness”, [“force over depth square”] would also “prove an exponent 2 instead of 3/2 on h”. And also earlier, these Authors had over and over stressed the self-similarity of parabolas as so-called proof of h² for cones and pyramids. But all parabolas with any exponent >1 are self-similar and quacking by putting the result already into the question for its “proof” is at best ridiculous. My finally desperate trial was with the Chinese Journal [18]. It has been explained that the early publication of [18] would have been the last chance to appear timely before the first of the three fatal airliner crashes over China, Indian Sea, and Ethiopia in short sequence. The FAA (Federal Aviation Administration) would have seen from the copied Figure 2, that phase-transitions by mechanical stress are extremely dangerous for the facilitation of the micro-crack formation (one or two μm long) with risks by following catastrophic crashes at higher forces, so that materials at the pickle forks of airplanes must consist of materials that must withstand phase-transitions against the highest forces from strong turbulences in hazardous areas. It was clear that such 1 to 2 μm length’ cracks on aluminium alloy surfaces would not have been seen at the legally enforced six-months’ routine checks of all active airplanes. They were never seen or looked for. In view of Figure 2 we can trust that FAA (some FAA representatives listened to my lectures in US (and we also discussed them, so that they knew my results) and looked for my publications. They would have immediately cared for improvements of safety checks with much higher precision in the indentations than before, as they did now. But that chance was lost due to the “Peer Reviewers delays”. As they have immediately enforced a 6 month’s recheck of all airplanes after the appearance of [18] for nano-cracks, they grounded the whole new fleet of 280 airliners apparently due to such micro-cracks on their pickle-forks that were not checked for before. This was their striking agreement for our physically correct search with exponent 3/2 on the nanoindentation loading parabola depth, revealing phase-transition forces (including phase-transition energy calculation). Thus instrument builders are well-advised to check every new material with instrumented microindentations for phase-transitions under load. These must have their kink-onsets at higher forces and their endothermic (that is further negative) phase-transition energies lower than related well-behaved materials (also subject to investigation). And NIST and ISO are advised to exit from the doubly unphysical indentation “14577 standards, because they are still retained by DIN” with the energy violation and the false exponent of their unphysical formulated 14577 standard. All of these 3 fatal crashes in short sequence could have been avoided by unblocked publication. The whole new fleet of the producer of these airliners was grounded for 28 months. That was shortly six months after the appearance with my copied Figure 2. It is required for the legally enforced rechecking of all active airplanes when such micro-cracks were now detected obviously with better techniques and thanks to the 4 years blocked appearance of [18].

Also necessary for reliable indentations are mechanically stressed turbines, windmills, bridges, buildings, earth-quake safe constructions, etc, etc. That is primarily important for new materials that must be safe for centuries. It is most easy with indentations in view of the copied Figure 2. We are thus confident, that NIST will no longer accept the shameful errors of DIN-ISO-NIST-14577 and that the physically correct analyses of nanoindentations will have a great future. Clearly, NIST must worldwide enforce the search for phase-transitions of materials with as high as possible phase-transition onset forces and favourable endothermic phase-transition energies by requiring correct instrumented indentation analyses. This will mostly require micro indentations. It is hoped that DIN will soon return for accepting easy understanding science. But majority votes of (shameful) Belief against undeniable Mathematics are out of question. All against one are so not possible with the present leading officials of DIN. However any other branches of the huge Organization without dichotomy of the officials can be more helpful in Germany. But the present DIN-ISO-NIST-14577 “standard” must be corrected in view of the risks for micro- cracks and catastrophic crashes. That is also necessary for mechanically stressed turbines, windmills, bridges, buildings, earth-quakes, safe buildings, etc, etc. That is primarily important for new materials that must be safe for centuries. It is most easy with indentations in view of the therefore here repeated Figure 2. We are thus confident, that NIST will no longer accept the errors of DIN-ISO-14577 and that the physically correct analyses of nanoindentations will have a great future.

None.

The Author declares that there is no conflict of interest.

1. Oliver WC, Pharr G M (1992) An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments. J. Mater Res 7: 1564-1583.
2. Kaupp G, Naimi-Jamal M R (2013) Penetration Resistance and Penetrability in Pyramidal (nano)Indentations. Scanning 35(2): 88-111.
3. Kaupp G (2022) Basic Mathematics for Physically Correct Mechanical Properties from Indentations. E-Book covering 16 open-access publications.
4. Kaupp G (2013) Penetration Resistance: A New Approach to the Energetics of Indentations. Scanning 35(6): 392-401.
5. Kaupp G (2017) The ISO Standard 14577 for Mechanics Violates the First Energy Law and Denies Physical Dimensions. Journal of Material Science & Engineering 6(1000321): 8.
6. Kaupp G (2016) The Physical Foundation of F_N = k h(3/2) for Conical/Pyramidal Indentation Loading Curves. Scanning 38(2): 177-179.
7. Merle E, Maier V, Durst K (2014) Experimental and theoretical confirmation of the scaling exponent 2 in pyramidal load displacement data for depth sensing indentation. Scanning 36(5): 526-529.
8. G Kaupp G (2024) A Way out of World-Wide Indentation Dichotomy in Materials' Science. Mod. Concept Material Sci. 6(2): 1-5.
9. M Troyon, F Annes, J A Garcia Guzman (2012) Is the Exponent 3/2 justified in analysis of loading curve of pyramidal nanoindentations? Scanning 34(6): 410-417.
10. Durst K, Backes B, Goken M (2005) Indentation Size Effect in Metallic Materials Correcting for the Size of the Plastic Zone. Scripta Materialia 52(11): 1093-1097.
11. Kaupp G (2024) Unexpected Twinning and Phase-Transition of the Indentation Standards, their Transition Energies, and Scientific Dichotomy. J. Appl. Math. Phys. 12: 2119-2159.
12. Malzbender J, De With G, Toonder J (2000) The p-h² Relationship in Indentation. J. Mater. Res. 15: 1209-1212.
13. Wang T H, Fang T H, Lin Y C (2008) Finite‐Element Analysis of the Mechanical Behavior of Au/Cu and Cu/Au Multilayers on Silicon Substrate under Nanoindentation. Appl. Phys. A 90: 457-463.
14. Kaupp G (2019) Phase-Transition Energies, New Characterization of Solid Materials and Anisotropy. Advances in Materials Physics and Chemistry 9(4): 57-70.
15. Kaupp G (2019) Physical Nanoindentations: From Penetration Resistance to Phase-Transition Energies. Adv. Mater. Phys. Chem. 9: 103-122.
16. Kaupp G (2020) Indentation onto Stishovite (SIO₂), MgO, and a Covered Superalloy: "Pop-in" Repair, Phase-Transition Onsets, Polymorph Energies, and Transiton-Energis. Advances in Materials Physics and Chemistry 10(3): 77-95.
17. Kaupp G (2023) Phase-Transitions at High, very High, and very Low Temperatures upon Nano-indentations: Onset Forces and Transition Energies. Adv. Mater. Phys. Chem. 13: 101-120.
18. Kaupp G (2018) Six Polymorphs of Sodium Chloride upon Depth-Sensing Macroindentation with Unusual Long-Range Cracks Requiring 30 N Load. Journal of Material Science & Engineering 7(4): 1000473.