 Review article
Review article
Heat Transport Equations in Elastic Nanosystems
Angelo Morro*
DIBRIS-Department of informatics, Bioengineering, Robotics and system Engineering University/Organization: university of Genoa, Italy
Angelo Morro, DIBRIS-Department of informatics, Bioengineering, Robotics and system Engineering university/Organization: University of Genoa, Italy
Received Date:February 07, 2024; Published Date:February 20, 2024
Abstract
The paper is devoted to some modelling equations for heat propagation in nanosystems. The purpose is to investigate the thermodynamic consistency so that appropriate constitutive restrictions are established. First a second-order differential equation is considered, with two phase lags, that fits experimental data on heat propagation in graphene. Next a non-local model is examined through a rate-type equation with second-order spatial derivatives of the heat flux. For generality the body is allowed to be elastically deformable. The thermodynamic consistency leads to some simplifications and relates the whole model to free energy function of temperature, strain, and heat flux.
Keywords:Heat propagation in graphene; Relaxation in nanosystems, Thermal wave equations; Non-local equations; Thermodynamic consistency
Introduction
The classical Fourier theory of heat conduction is widely applied in thermal processes also because of its simplicity and reliability in many thermal processes. It is based on Fourier’s law for the heat flux q,
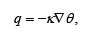
where θ is the (absolute) temperature, Δ denotes the gradient and κ is the conductivity. Yet there are many contexts where Fourier’s theory is inadequate. Conceptually, it is paradoxical that a theory predicts propagation with infinite speed as is the case for Fourier’s theory. The Maxwell-Cattaneo (MC) equation [1-3].
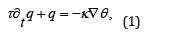
where τ is a time constant and ∂t is the partial time derivative avoids the paradox of infinite speed of propagation. Indeed, a wide literature has been developed as to the proper formulation in that eq. (1) is viewed as a constitutive equation and accordingly it has to satisfy the objectivity principle and to be thermodynamically consistent. Among others, refs [4-8] give exhaustive accounts of these topics and their developments in the literature.
Now, though the MC equation remedies the paradox, there are experiments on heat propagation in graphene [9] whereby an equation more involved than (1) is appropriate to fit the results. Indeed a good fit has been obtained with the equation
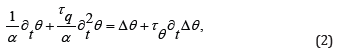
where α is the thermal diffusivity, τq,τθ two relaxation times or phase lags, and Δ is the Laplacian operator. Indeed, the fact that the fitting indicates comparable values for τqandτθ, respectively 1.85 and 1.01 ps, makes eq. (2) worthy of attention. Accordingly, though eq. (2) is again plagued by the paradox of infinite speed of propagation, it is of interest to clarify the origin of (2) and to cast it in a context of continuum physics.
Other experiments [10] show a good fit with the solution of the Guyer-Krumhansl equation,
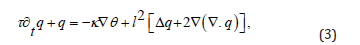
a linear approximation of the nonlinear Guyer-Krumhansl equation [11, 12]
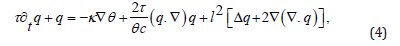
where c is the specific heat and l a parameter justified by phonon processes. Nanodevices suffer from dissipation of heat at a rate that is not explained by the previous equations. Consistently, the decrease of the thermal conductivity (see, e.g., [10, 13, 14]), which hinders heat exchange, calls for more involved materials models. Furthermore, nanoscale systems with dimensions comparable to the mean-free path of particles (or phonons) non-local effects are required to be inserted in the model. In addition, in microdevices working at high frequencies also relaxation effects occur so that realistic models need to account for the time delay of relaxation processes.
Based on these observations, this paper has a twofold purpose. First to investigate the appropriate continuum framework for equations of the form (2). Secondly, to examine non-local generalizations of (4) and to establish the restrictions placed by the thermodynamic consistency.
Balance equations and entropy principle
The body under consideration occupies a time-dependent region Ω. A point of the body is labelled by the position vector X in a reference configuration R. Hence we let X = χ (X, t ) provide the position x in Ω in terms of the position X∈ R and the time t. The body is deformable and we let, F,Fik=∂Xkχi, be the deformation gradient. The velocity v is defined by v=∂tχ while ∇=∂x is the gradient operator. The tensor L denotes the velocity gradient,Lij= ∂xjvi. We let ρ be the mass density, T the Cauchy stress, ε the internal energy density, and η the entropy density (per unit mass). For any pair of vectors a,b we let a ⋅b denote the inner product; likewise for any pair of tensors A,B we let A⋅B =AijBij For any function f (Χ,t ) we denote by a superposed dot the material derivative and we have f=∂tf+(v⋅∇)f. The superscript T means transpose of a tensor, sym the symmetric part, and skw the skew-symmetric part; 1 denotes the unit second-order tensor and ⊗ the dyadic product.
By the conservation of mass, the mass density ρ is subject to the continuity equation

The equation of motion is given the form

where b is the body force and (∇ ⋅T)i=∂xj Tij By the balance of angular momentum it follows T = TT . The balance of energy leads to the equation
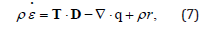
where r is the (external) energy supply, q is the heat flux, D = symL is the stretching tensor. The balance of entropy is written in the form
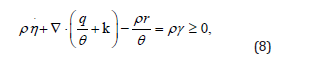
which means that q/θ + k is the entropy flux, r/θ the entropy supply and γ the rate of entropy production; the assumption γ ≥ 0 specifies the law of increase of entropy. Equation (8) is referred to as Clausius-Duhem (CD) inequality. We state the entropy principle as follows: physically admissible models are required to satisfy the CD inequality (8) subject to the balance equations (5)-(7).
Substitution of (∇ ⋅ q −ρ r )/θ from (7) yields
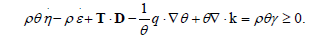
Using the Helmholtz free energy
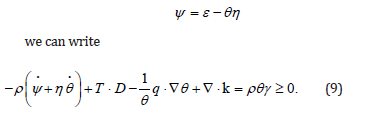
Heat transport equation with two phase lags
The unusual form of (2) calls for a possible physical model. Let the body be rigid and assume
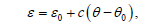
the specific heat c being a positive constant. Hence the balance of energy results in
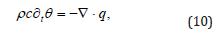
where no heat supply is allowed. The heat conduction consists of two fluxes, q1,q2, with
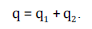
The flux q1 represents heat conduction due to light particles (electrons) and then modelled by a Fourier law,

The flux q2 describes heat conduction of heavy particles (ions) and hence is affected by a relaxation property; we model this property by the MC law
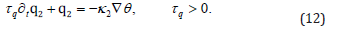
Both κ1 and κ2 are constant, symmetric, non-singular tensors. Time differentiation of (11) gives

while (10) leads to

Hence by (10) plus τq times (14) we obtain
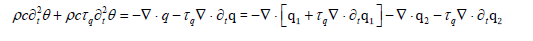
and then
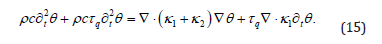
In isotropic materials we have
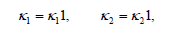
and hence (16) becomes
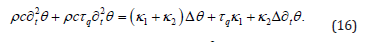
If, as we prove in a while, κ1 and κ2 > 0 we can define
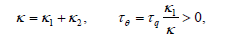
and hence eq. (2) follows with α =κ/ρc
We now investigate the thermodynamic consistency of the model (11)-(12). body is undeformable (D = 0) then the CD inequality simplifies to
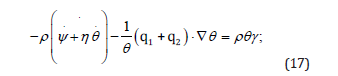
the assumption k = 0 will be shown to be consistent with the constitutive equations. Owing to eqs. (11)-(12) we let
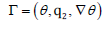
be the set of variables. Time differentiation of ψ (θ,q2,∇θ) and substitution in (17) results in
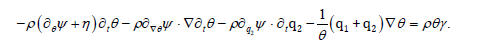
Substitution of ∂t q2 from eq. (12) leads to
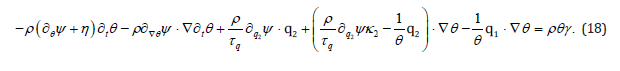
The linearity and arbitrariness of,∇∂tθ,∂tθ imply
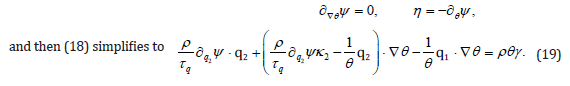
Assume q1→0 as∇θ →0 (which is obviously true for (11).
Hence eq. (19) implies that
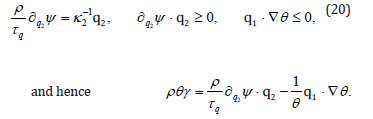
The obvious integration of the first condition in (20) yields
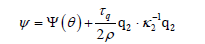
and, by the inequalities in (20) we find
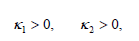
Consequently, the model (10)-(12) with two different fluxes is consistent with thermodynamics provided only that the conductivity tensors κ1,κ2 are positive definite.
A simpler derivation of (2) is obtained by considering a formal generalization of the MC equation in the form
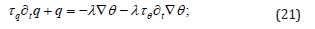
if τ0=0 we recover the MC equation. To obtain the differential equation (2) we assume the balance of energy in the form (10) so that
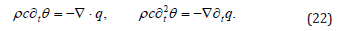
Computing the divergence of (21) and using (22) we find (2) with α = λ/ρc
Non-local models of heat conduction in elastic nanosystems
The possible large values of spatial gradients, of temperature and heat flux, in nanosystems motivate both non-local terms and the time derivative of the heat flux in the modelling of heat conduction. To fix ideas we observe that quite a general equation has been considered in [1] in the form
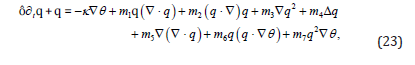
where q2 = q ⋅ q and the coefficients m1,m2,...m7 are allowed to depend on temperature.
This indicates that a thermodynamically consistent scheme embodying in some way eq. (23) needs θ ,q,∇θ ,∇q,∇∇q among the variables.
As a further generalization we let the nanosystem be deformable and hence we let the material properties be affected by the deformation gradient F. Hence we let
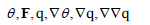
be the variables describing the nanosystem. Indeed, the scalars ψ and ε should depend on invariants of F; for definiteness we then assume that ψ depends on F through the Green-Lagrange strain
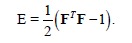
By the objectivity principle ([6], ch. 4; [7], § 1.9) the constitutive equations are required to be form-invariant under Euclidean transformations. This means that the constitutive equations involve scalars, vectors, and tensors relative to Euclidean transfor-mations. The time derivative is not form invariant; the transform of the time derivative is different from the time derivative of the transform. That is why objective time deriva-tives are used for rate equations in continuum mechanics. The simplest objective time derivative is the corotational one, namely
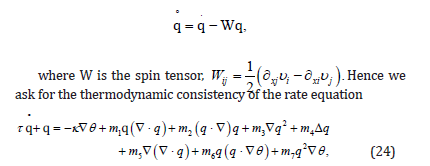
Equation (24) can then be viewed as a constitutive equation for the rate q in terms of the variables θ ,F,q,∇θ ,∇q,∇∇q, where
m1,m2,...m7 may depend on θ and F, possibly through J = det F. Notice that eq. (24) implies
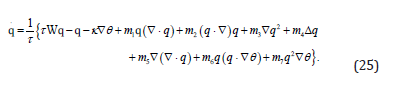
We then start with the assumption
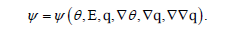
Compute.ψ , substitute in the CD inequality (9) and divide by θ to obtain
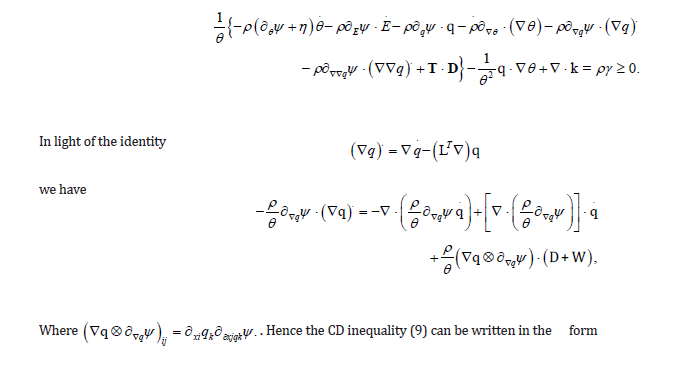
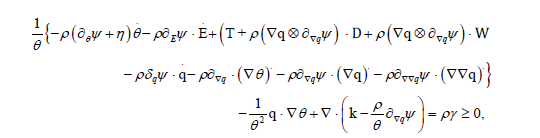
where qδ ψ is the variational derivative,
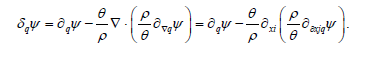
The derivative q is not arbitrary in thatq = q+ q W is given by eq. (24). Furthermore.E and D are related by the identity E = FT F.
Hence upon substitution of.q from (24) and multiplication by θ we have
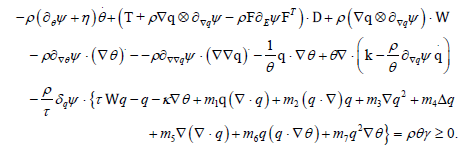
This form of the CD inequality allows us to see the possible arbitrariness and hence to find the corresponding consequences. First we notice that (∇θ ) ,(∇∇q) ,θ can take arbitrary values and meanwhile without affecting the constitutive functions ψ ,η,T,k,γ . Owing to the linearity it follows that
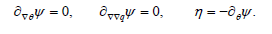
The linearity and arbitrariness of W and D imply that
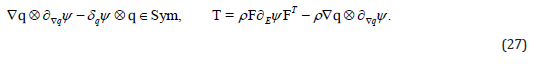
Hence we are left with
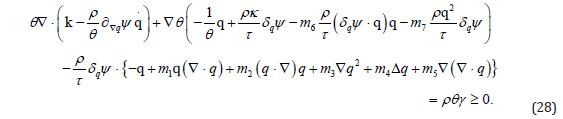
Definite consequences of inequality (28) follow in particular cases. Assume m1,m2,m3 = 0. We notice that
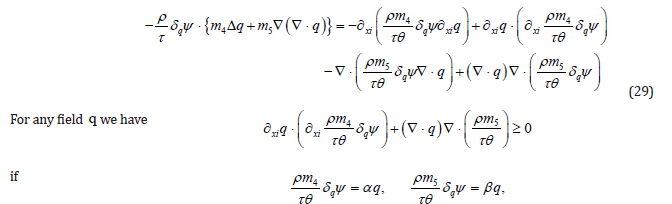
where α ,β are positive constants. Assuming it is so we can use (29) and write eq. (28) in the form
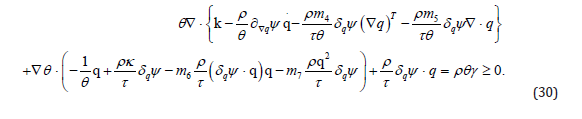
Inequality (30) holds if
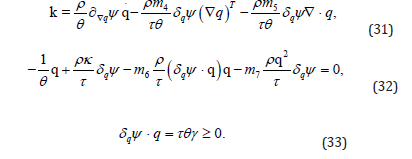
The reduced inequality (33) implies that
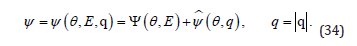
Equation (32) then simplifies to
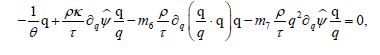
whence
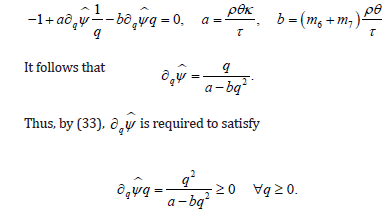
As it follows by letting q →0 and q →∞ we find the necessary and sufficient conditions
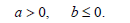
Consequently we find that
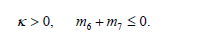
If b < 0 then it follows
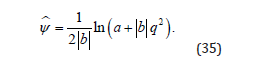
If, instead, b = 0 then
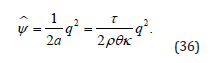
Since we have assumed m1,m2,m3 = 0 then the non-local model is thermodynamically consistent if it is settled as follows. The heat flux q is governed by the rate equation
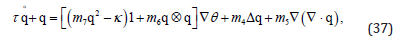
where m4,m5,m6,m7 are allowed to depend on temperature. The entropy principle ulti-mately requires that
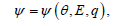
where q = q . For definiteness we assume ψ in the form (34) and then we find that if
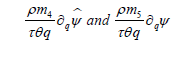
are constants then
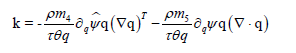
is the extra-entropy flux and
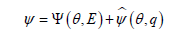
Conclusions
This paper deals with two model equations for heat propagation in nanosystems. The equation with two phase lags (2) is shown to arise from a physical model with two heat fluxes, one for the Fourier- type for light particles (possibly electrons) and one for heavy particles (possibly ions) which involve a relaxation term. The whole physical scheme is found to be thermodynamically consistent.
The second equation is non-local in character in that involves higher-order spatial derivatives of the heat flux thus generalizing the linear Guyer-Krumhansl equation (3). For generality the body is allowed to be elastically deformable. The thermodynamical consistency is then proved for the non-linear objective rate equation (37) subject to
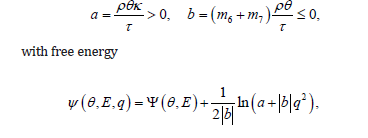
with q = q . The dependence on b generalizes previous models by allowing for the non-linear terms parameterized by m6 and m7 . If 0 b = then ψ is given by (36).
the stress emerge through the formal dependence of the free energy on ∇q. Hence the stress behaviour is not affected by letting the objective derivative be the corotational one and the free energy be independent of ∇q. This indicates the guideline for a simple model accounting for heat conduction with non-local and non-linear properties.
Acknowledgement
The research leading to this work has been developed under the auspices of INDAM-GNFM.
Conflict of Interest
None.
References
- Y Guo, D Jou, M Wang (2017) Macroscopic heat transport equations and heat waves in nonequilibrium states. Physica D: Nonlinear Phenomena 342: 24-31.
- JC Maxwell (1965) On the dynamic theory of gases. in The Scientific Papers of JC Maxwell 2: 26-78.
- C Cattaneo (1948) Sulla conduzione del calore. Atti Sem Mat Fis Univ Modena 3: 3-21.
- R Kovacs (2024) Heat equations beyond Fourier: From heat waves to thermal metamaterials, Physics Reports 1048: 1-75.
- B Straughan (2011) Heat Waves, Springer, New York, USA.
- C Truesdell (1977) A First Course in Rational Continuum Mechanics. vol. 1, Academic Press, New York, USA.
- Morro C Giorgi (2023) Mathematical Modelling of Continuum Physics. Birkhauser, Cham.
- DD Joseph, L Preziosi (1989) Heat Waves. Rev Modern Phys 61: 41-73.
- J Zhang, X Huang, Y Yue, J Wang, X Wang (2011) Dynamic response of graphene to thermal impulse. Phys Rev B 84: 235416
- Hennessy MG, Myers TG (2020) Guyer-Krumhansl heat conduction in thermore-flectance experiments, in Multidisciplinary Mathematical Modelling. Applications of Mathematics to the Real World, F. Font and T.G. Myers eds pp. 21-34.
- VA Cimmelli, A Sellitto, D Jou (2010) Nonequilibrium temperatures, heat waves, and nonlinear heat transport equations. Phys Rev B 81: 054301
- Morro (2023) On the modelling of heat conduction in crystals via higher-grade terms. Nanotecnol Adv Mater Sci 6: 1-4.
- Cahill DG (2014) Nanoscale thermal transport. II Appl Phys Rev 1: 011305
- Dong Y (2015) Dynamical Analysis of Non-Fourier Heat Conduction and Its Appli-cation in Nanosystems, Springer, New York, USA.
-
Angelo Morro*. Heat Transport Equations in Elastic Nanosystems. Mod Concept Material Sci. 5(5): 2024. MCMS. MS.ID.000621.
-
Heat propagation in graphene, Relaxation in nanosystems, Thermal wave equations, Non-local equations, Thermodynamic consistency
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






