Early confirmative work of the Association-Induction Hypothesis

While membrane theory is a central concept in physiology, which assumes that transmembrane ion transport is responsible for the generation of membrane potential, there is other littleknown theory, Association-Induction Hypothesis (AIH) put forward by Gilbert Ling [1, 2]. His most notable prediction is that the membrane potential is generated by a binding of mobile ions through their adsorption, but this prediction is totally at odds with membrane theory. Despite almost general recognition of membrane theory, some people are still interested in the AIH today. Bagatolli pointed out that the cell is not in an ideal thermodynamic state and should be considered as a kind of colloidal material, that is, cellular activities can only be theorized from the point of view of thermodynamics for the real system instead of the ideal system [3,4]. Bagatolli’s view is in line with Ling’s AIH, which states that it is wrong to treat cellular water thermodynamically as free water, as the actual activity of cellular water is considerably reduced [1,2]. Consequently, thermodynamic treatment of water and consideration of such low water activity are necessary to theorize the activity of living cells. Schneider emphasizes that physiology should be framed within thermodynamics. But at the same time, he suggests that thermodynamics is not used in the right way in today’s physiology. Indeed, we regard the living cell as overly idealized matter. This is what Schneider expresses most typically in his words the cell is not a bag filled with “free” water with floating organelles, but the water is in a more ordered state, rather like a liquid crystalline [5]. This view of water, the importance of liquid crystalline water for the living cell had been for long while advocated also by Ling, has been repeatedly reported especially by Pollack over the past two decades [6,7].

In short, throughout his scientific career, Ling defended the idea that cellular activities (the generation of a membrane potential, the transport of substances across the cell membrane, etc.) are explicable simply as consequences based on old-fashioned wellestablished ordinary thermodynamics and physical chemistry. He even declared that ion channels and membrane pump were not necessary for the activity of living cells [1,2].

Wnek et al. addressed this point, particularly with regard to the membrane potential. He studied the characteristics of the cell potential and found that potential characteristics similar to those of the living cell can be observed even in non-living systems [8].

Thus, their findings suggesting that membrane potential characteristics are not unique to the living system are in agreement with Ling’s opinion, and their work is strongly supported by experimental evidence. Funk and Scholkmann also broach this subject, suggesting that the origin of membrane potential has not been resolved, but still remains a controversial question [9].

During our investigation about the membrane theory and the AIH, we came across an intriguing work by Shinpei Ohki and Osamu Aono, which was performed more than forty years ago. Ohki had done countless physiological works by wielding his deep theoretical knowledge of physical chemistry and physiology [10]. One of his works, “Membrane Potential of Squid Axons...” performed with his colleague Aono [11], deals with the measurement of membrane potential and its analysis using membrane theory. However, their work clearly demonstrates the validity of Ling’s point of view. Ohki and Aono never sided with Ling’s viewpoint while pointing out that the Goldman-Hodgkin-Katz equation (GHK eq.), which is a fundamental concept of membrane theory, cannot reproduce experimentally measured membrane potential characteristics. Ohki and Aono suggested that the surface potential due to electrical charges on the membrane should be taken into account in order to theorize the membrane potential, but that is also very the essential view of the AIH. Ohki must have been familiar with Ling’s AIH as he discussed Ling’s work in his article [10], and both he and Aono cited one of Ling’s works, ref. [12], in their work, ref. [11].

In this paper, we examine the work of Ohki and Aono (ref. [11]) from the point of view of the AIH and explain that they inadvertently obtained results in harmony with the AIH. We also further suggest that the AIH is by far superior to the membrane theory for theorizing the cell activity.

Membrane theory and AIH

Membrane theory is one of the main electrophysiological concepts [1, 2]. It attributes the origin of membrane potential to transmembrane ion transport. Without ion transport, the membrane potential is even unthinkable within the framework of membrane theory. On the other hand, AIH attributes the origin of membrane potential to ion adsorption: spatial immobilization of mobile ions by their adsorption to cellular constituents, such as proteins and lipids, results more or less inevitably in a heterogeneous distribution of ionic charges. Such a heterogeneous distribution of ionic charges results in a nonzero potential. This nonzero potential is merely a consequence predicted by the ordinary electromagnetism, but it is the membrane potential in the AIH. Conversely, the AIH means that the existence of transmembrane ion transport has no bearing on the generation of the membrane potential. The AIH is the simplest and most solidly supported electromagnetic, physical, and chemical explanation for the generation of membrane potential. Surprisingly, the AIH which is supported by the basic physics has received less attention from the physiological community to date.

Potential characteristics by the AIH prediction Prediction 1

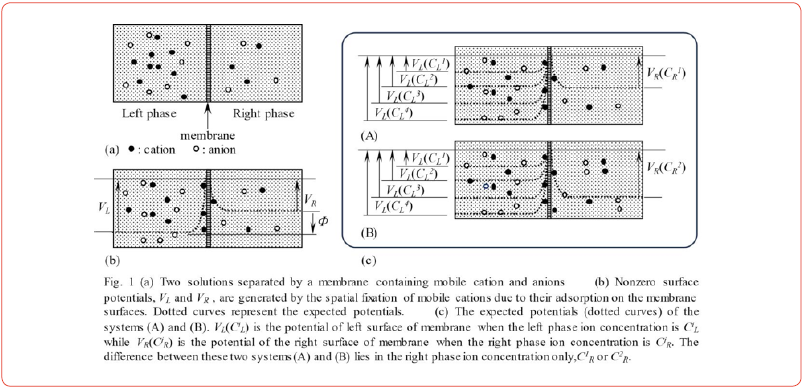
Figure 1(a) shows two electrolytic solutions separated by a membrane. This is a model of a living cell. The left and right phases correspond to the intracellular and extracellular phases, respectively, and the membrane corresponds to the plasma membrane. Some ions adsorb on the membrane, as shown in Figure 1 (b). This means that a heterogeneous ion distribution takes place in both the left and right phases. Heterogeneous ion distribution inevitably leads to a nonzero potential, as predicted by electromagnetism. The dotted curves in Figure 1(b) represent the expected potential profiles, where V_L and V_R represent the membrane surface potentials.

The AIH states that the nonzero potentials V_L and V_R are generated independently of each other, and Eq. 1 gives the membrane potential. Therefore, ion adsorption is essential for membrane potential generation, but transmembrane ion transport has nothing to do with membrane potential generation. Even the potential across the impermeable membrane can be explained by the AIH.

Here we consider the experimental system illustrated in Fig. 1(c) (A), with two solutions separated by an “impermeable” membrane. Let us imagine that we are measuring the potential across this impermeable membrane when the left-phase ion concentration Cⁱ_L (1, 2,3, 4) varies from 10⁻⁵ M to 1 M while keeping the right-phase ion concentration C^l_R constant. The AIH states that V_R(C^l_R) is constant, since C^l_R is kept constant. Therefore, the membrane potential given by Eq. 2,Φ_A (Cⁱ_L;C^l_R) is a function of a variable of Cⁱ_L and C^l_R is a kind of parameter. Variation in Cⁱ_L inevitably leads to a variation in the amount of adsorbed ions on the left surface of the membrane. Consequently, V_L(Cⁱ_L)inevitably varies as a function of Cⁱ_L, with the dotted curves in Fig. 1 (c) (A) representing the expected potential profiles. The same applies to the system shown in Fig. 1(c) (B), and Eq. 3 is derived when V_R (C²_R) is constant. Consequently,Φ_B(Cⁱ_L;C²_R) is a function of Cⁱ_L and C²_R is a parameter.

Membrane potential of the system in Fig.1(c) (A)

Membrane potential of the system in Fig.1(c) (B)

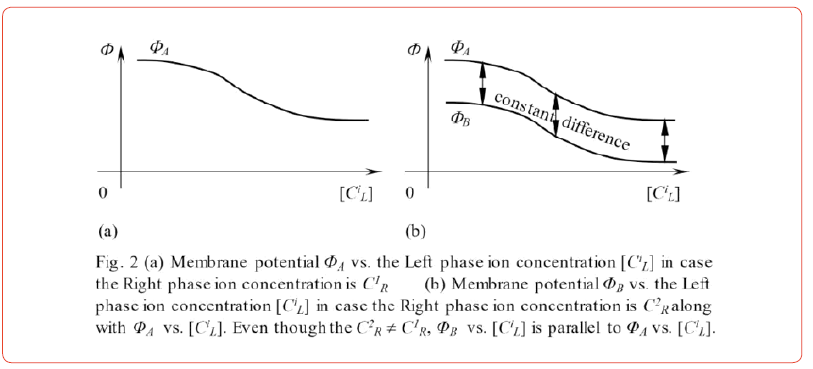
Eqs. 2 and 3 have been derived using the AIH. They lead to a mathematical relationship given by Eq. 4. This relationship suggests that the potential difference between the two systems illustrated in Figures 1(c) (A) and (B) is constant independently of Cⁱ_L. To be more precise, if the potential of Φ_A is represented as shown in Figure 2(a), the profile of _BΦ is different from Φ_A only by a constant value independent of [Cⁱ_L] as illustrated in Figure 2(b). This is one of the most notable consequences of the AIH. Membrane theory cannot lead to this result since we are discussing the system in which the “impermeable” membrane is employed in the first place.

Membrane potential is merely the potential difference between two phases, which are generated independently from each other. Eq. 4 is one of the noticeable consequences of the AIH.

Prediction 2

The typical GHK eq. is given by Eq. 5. But our previous work based on the AIH suggests that the potential Φ should be given by Eq. 6 where K_i is the binding constant between the ion i and the adsorption site for i [13]. If the membrane permeability is zero, Eq. 5 (i.e.P_i=0) collapses. But Eq. 6 holds as long as ion adsorption is the determining factor in membrane potential generation, regardless of the membrane permeability.

< Prediction 2> Potential is generated by the ion adsorption as typified by Eq. 6 regardless of the membrane permeability to ions.

The consequences, which are introduced in the previous section, will be experimentally verified in this section.

Verification of the < Prediction 1>

We measured the potential generated across an impermeable membrane separating two aqueous ionic solutions. The experimental setup is basically the same as that illustrated in Figure 1. We used lithium glass LICGC^TM AG-01 (OHARA, Kanagawa, Japan) as the membrane, and the left and right phase solutions are LiCl solutions. The potential across the lithium glass was measured by varying the concentration of LiCl in the left phase from 10⁻⁵ M to 1 M, while the concentration of LiCl in the right phase remained constant.

Figure 3(a) shows the result. Any pair of potential curves maintains a constant potential difference as long as [ ]L LiCl is identical. For example, let us take the potential data represented by ○ and × in Figure 3(a). When log₁₀[LiCl]_L=−5 the potential difference between them is 0.131 V. When log₁₀[LiCl]_L=−2 the potential difference between them is 0.127 V. Thus, their potential difference is almost constant ~ 0.13 V as long as [LiCl]_L is identical for ○ and ×. This feature is consistent with the described in the previous section. It can be quantified mathematically by Eq. 4. Agreement of the characteristics of the potential data with Eq. 4 suggests the validity of the AIH.

Katoh et al. describe that lithium glass is permeable to Li⁺ [14]. Consequently, it is important to analyze whether the GHK eq. can reproduce the membrane potential in Figure 3(a). Eq. 7 is the GHK eq. for this system. We tried to compute the experimentally measured potentials in Figure 3(a) using Eq. 7. However, we found that the computed potential does not necessarily reproduce the experimental potentials. The disparity between the experimental and computational potentials becomes non-negligible when log₁₀[LiCl]_R=−5 M as shown in Fig. 3(b) (the computational potential reproduces the experimental potential only when [LiCl]_L=10⁻⁵M Thus, the GHK eq. is not tenable, and we can say that the membrane theory is indefensible.

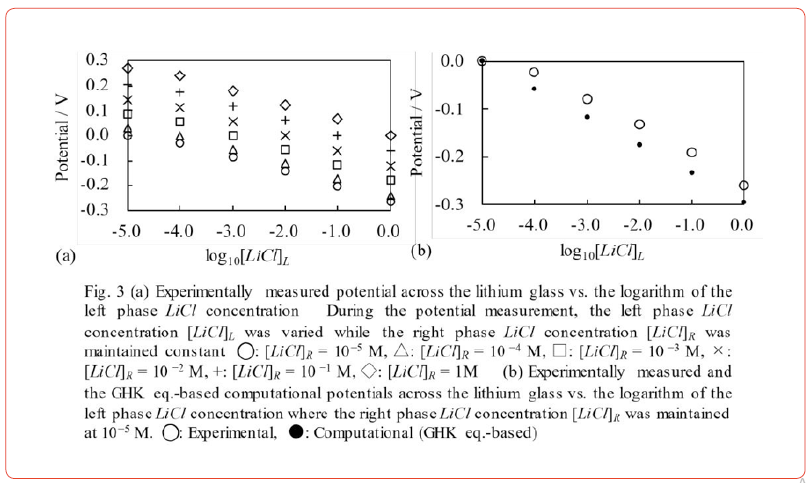
However, irrespective of the membrane’s permeability to mobile ions, the AIH is in harmony with the experimental fact illustrated in Figure 3(a), which is in agreement with < Prediction 1>. We assume that Li⁺ is adsorbed onto lithium glass surfaces, which is in contradiction to the report by Kato et al. in ref. [14].

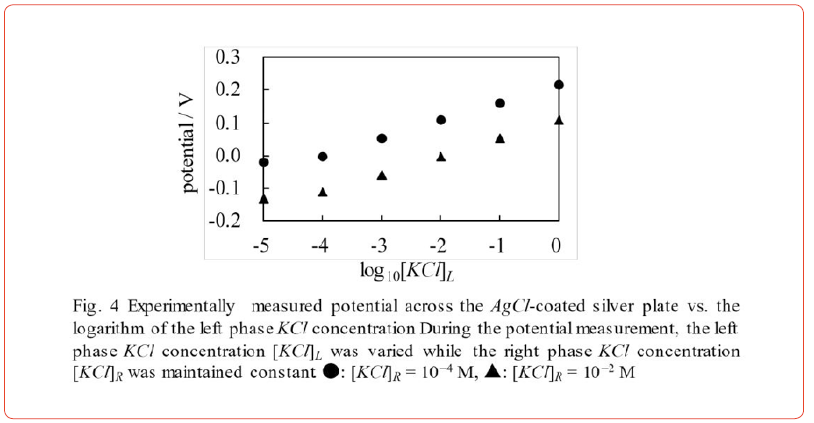
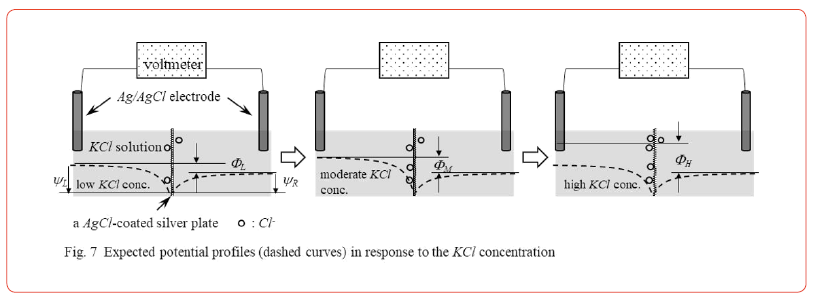
We performed the same experiment using an AgCl − coated impermeable silver plate in place of lithium glass and using KCl solutions in place of LiCl solutions. Experimental data when [KCl]_R=10⁻⁴M and 10⁻²M only are shown in Figure 4 (too much data makes the diagram too cluttered). The potential difference between these two curves is constant. Therefore, < Prediction 1> is again sufficient. Figure 4 is therefore a proof of the validity of the AIH. Of course, we have confirmed that the experimental potential data when [KCl]_R is different from 10⁻⁴M and 10⁻²M are sufficient for the < Prediction 1> (these data are not shown here).

Verification of the < Prediction 2>

First, we focus on Figure 3(a). The AIH-based equation (Eq. 6) can explain this, assuming that Li⁺ adsorbs onto lithium glass. We have indirect evidence suggesting that Li⁺ adsorbs on the surface of lithium glass, and we will show the abstract below.

Figure 5(a) illustrates a lithium glass and a metal wire bonded with an electrically conductive adhesive; we refer to it hereafter as meLiGlass. A lithium glass was inserted on the surface of a LiCl solution so that the bottom surface of the lithium glass was in contact with the surface of the LiCl solution, as shown in Figure 5(b). The “surface potential” of the meLiGlass was then measured by varying the concentration of LiCl. It should be noted that the generated potential cannot be the membrane potential, since this system is a single-phase solution.

Figure 5(c) (A) represents the model of the experimental setup in Figure 5(b). Assuming that Li⁺ adsorbs onto the lithium glass surface, the expected surface potential is assumed to increase V_L>V_M>V_H as the concentration of Li⁺ increases, as shown in Figure 5(c) (B). The experimental result shown in Figure 6 exhibits the expected characteristics.

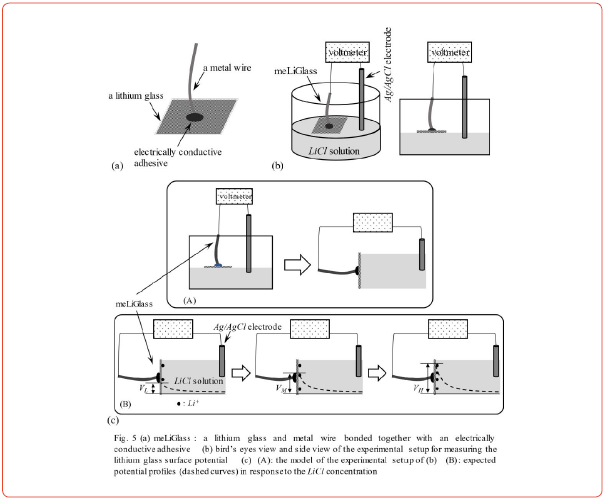
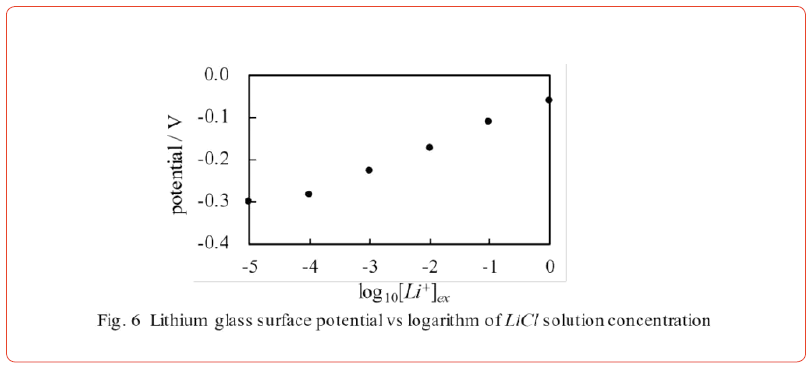
Our previous works [13, 15] suggest that the potential formula based on the AIH is given by Eq. 6, which can be derived by evaluating the surface potential generated on the membrane surfaces (the exact procedure is described in the refs. [13, 15]). We consider the system illustrated in Figure 5(b) in the same way. We derived the surface potential formula Eq. 8 on the assumption that Li⁺ adsorbs on the surface of lithium glass and is responsible for the generation of the potential. We have confirmed that Eq. 8 reproduces the experimental data in Figure 6 by appropriately determining the numerical values of K_Li and A (See again especially the ref. [15] for deriving Eq. 8). The factor governing membrane potential generation must be ion adsorption, as predicted by < Prediction 2>.

Figure 4 is another verification of and is detailed as follows: Temsamani and Cheng suggest that Cl⁻ can adsorb onto AgCl [16]. Consequently, Cl⁻ must adsorb onto the surface of the AgCl− coated silver plate as shown in Figure 7 and the potential must be generated as indicated by the dashed curves. We measured the true potential through the AgCl− coated silver plate. During the measurement, the concentration KCl in the right phase was kept constant, while the concentration KCl in the left phase was varied. For example, when the concentration of KCl in the right phase is kept constant ( [KCl]_R=10⁻⁴ M or 10⁻² M), the amount of Cl⁻ adsorbed on the right surface of the silver plate coated with AgCl never changes, as illustrated in Figure 7. Consequently, the potential profile of the right phase never changes. However, the amount of Cl⁻ adsorbed on the left surface of the AgCl− coated silver plate changes as a function of the concentration of KCl in the left phase. The potential generated across the AgCl− coated silver plate is given by Eq. 9 where the definitions of ψ_i are illustrated in Figure 7. The value _Lψ is given by Eq. 10 like Eq. 8. Consequently, Φ_i is given by Eq. 11. We have confirmed that Eq. 11 quantitatively reproduces the experimental data in Figure 6. So, this is another proof of the validity of < Prediction 2>, and at the same time, the constant potential difference between the potential data represented by ● and ▲in Fig. 4 also suffices for < Prediction 1>.

Verification of < Prediction 1>

We will now show and discuss the work of Ohki and Aono [11], which was reported over forty years ago. They measured the potential generated across the plasma membrane of the axon by controlling the concentrations of intracellular and extracellular ions.

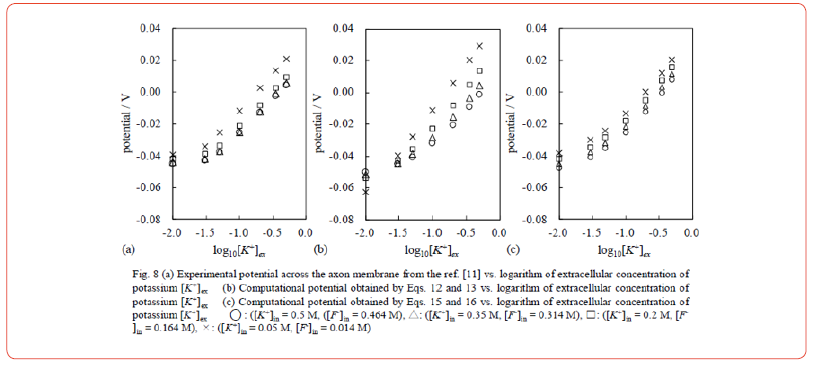
The intracellular ionic composition remained unchanged during the potential measurement, while the extracellular potassium concentration was altered. This experimental procedure is virtually the same as that used to obtain the diagrams in Figures. 3(a) and 4. The measured potential data are presented in Figure 8(a) where the intracellular ionic composition is indicated in the figure legend. We note that any pair of potential data curves in Figure 8(a) is basically sufficient for Eq. 4 as long as log₁₀ [K⁺]_ex >-1.5 Thus, < Prediction 1> is basically satisfied and can be interpreted as a proof of the validity of the AIH. However, Ohki and Aono attempted to explain the potential data in Figure 8(a) using the GHK eq., but they found that the GHK eq. could not reproduce the potential profiles unless the permeability coefficient was a variable and also depended on the environmental solution and composition. Intriguingly enough, they even say “A part of the dependence may be explained by taking into account the surface potential due to electrical charges on the membrane”, and this comment is in agreement with the AIH although they trust the membrane theory.

Verification of < Prediction 2>

Ohki and Aono attempted to reproduce the potential data in Figure 8(a) using the GHK eq. from Eq. 12. But they couldn’t find the right permeability coefficient as described in the section 4.1. They found the permeability coefficient relationship given in Eq. 13, but it was not satisfactory. Figure 8(b) shows the computational potential profiles obtained by Eqs. 12 and 13. The potential profiles in Figure 8(b) do not reproduce the potential profiles in Figure 8(a). Of course, the potential profiles of Figure 8(b) cannot suffice Eq. 4. Ohki and Aono also describe that the experimentally measured potential is not so sensitive to the intracellular potassium concentration, contrary to the prediction of Eq. 12.

We will now reexamine the potential data of Eq. 12 in the context of the AIH in the following way: We transform Eq. 12 into Eq.14.

The i K of Eq. 14 represents the binding constant. Then we turn to the binding reaction between the mobile ion and the membrane surface. Binding is, of course, dependent on the characteristics of the binding site, such as its structure, density, and so on. It is unlikely that the characteristics of the binding site on the outer surface of the axon are exactly the same as those on the inner surface of the axon. Therefore, it is natural to assume that the binding constant depends on where the binding occurs. For example, the binding constant on the outer surface of the axon, K_K^ex , must be different from the binding constant on the inner surface of the axon, in .

Therefore, it is assumed that the binding constants K_i^ex and K_iⁱⁿ need not be identical and that Eq.14 should be modified to Eq. 15. In other words, intracellular potential generation is independent of extracellular potential generation and vice versa. This concept is widely known as the AIH principle.

Assuming Eq. 16, the potential computation was performed using Eq. 15. The result is shown in Figure 8(c). Although there is still some disagreement between the computational result and the experimental result shown in Figure 8(a), the data agreement improved significantly.

In summary, Eq. 16 suggests that ion binding (adsorption) is the determining factor in potential generation. This conclusion is in line with < Prediction 2>. We should add a few comments: Importing the type of parameters (K^j_i,i=k,Na,Cl,F j=in,ex ) we wish seems unscientific or absurd, and it is quite understandable to think that they should have been experimentally measured quantities. However, even the permeability coefficients in the GHK eq. are not always experimentally measured but are determined so that the GHK eq. can reproduce the experimentally measured membrane potential [17-20]. Therefore, if the way to determine the numerical value of K^j_i described above is scientifically inappropriate, so is the prevailing procedure for finding the numerical value of P_i from the GHK eq. We believe it is necessary to reexamine previous works by taking into account both the membrane theory and the AIH. Currently, it is not fair to exclude the AIH as a physiological theory.

Ohki did not blindly deny the AIH. He examined the AIH and concluded that the AIH was not correct in his article [10]. He addressed the membrane theory in the same article [10] and concluded that the membrane theory was more correct. He cited a number of works published by other researchers and explained why the AIH is not sufficiently valid and why the membrane theory seems correct. His conclusion is not based on superficial ideas. Ling, on the other hand, came to the opposite conclusion. He disproved membrane theory and created a new physiological concept called AIH [1, 2]. Ling also put considerable effort into identifying previous publications. Neither Ohki nor Ling had done a botched scientific job. Both Ohki and Ling refer to a number of scientific works by other researchers [1, 2, 10], and these works are replete with experimental data. But they came to opposite conclusions: Ohki sided with the membrane theory, while Ling presented the AIH. But such a problem is not so uncommon in physiology. For example, one of the authors of this paper and his collaborator, Tamagawa and Ikeda, previously suggested that the ion adsorption model based on the AIH can quantitatively reproduce the experimental membrane potential theoretically [13], though the conventional theory, the membrane theory, attributes the membrane potential generation to the transmembrane ion transport [1, 2]. We will show another example from Ling’s book [1]: Imagine that a protein is dissolved in water. The structure of this protein is extraverted (the NH group and/or oxygen atoms are exposed to water in the bulk phase). The water molecules on the extraverts are polarized and these water molecules exhibit a decrease in solvency. On the other hand, if the same protein structure assumes that the introverts (the NH and CO groups are enclosed by the H bond) are not available to interact with water. Water molecules are not polarized by introverts. Water of this type does not exhibit a decrease in solvency. Water is often used as a solvent with proteins in physiological work, but even a simple and ubiquitous molecule such as water exhibits varied characteristics, depending on slight differences in conditions. Some may not think that water’s characteristics are variable. But such improbable characteristics of water have been frequently reported particularly by Pollack [6,7,21-26]. So, it’s not so easy to derive a right conclusion even from a simple experimental work. Therefore, Ohki and Aono came to side with the membrane theory despite their research results in favor of AIH [10,11]. What do we need to do to get around the difficulties, perform the right experiments under the right conditions, and draw the right conclusions? We believe that physiologists need to take a thermodynamic and physical chemistry views of the real system. As a matter of fact, theoreticians have already come by such a tool a century ago [27]. However, it is not so wide-spread in physiology field even today. Thermodynamics and physical chemistry for the real systems (not ideal systems) are needed since the biological phenomena never exhibit the thermodynamically ideal characteristics. We have to consider the experimental system as a thermodynamically real system.

The Association-Induction hypothesis was long rejected by mainstream physiology, while membrane theory has been the central concept of physiology. However, the work done by Ohki and Aono more than forty years ago clearly validates the Association- Induction hypothesis. Nevertheless, Ohki and Aono did not endorse this theory, but rather the membrane theory. This means that there exists the difficulty in drawing the right conclusion even in a simple experimental system. To overcome these difficulties, we should reconstruct physiology on the basis of physical chemistry and thermodynamics for the real system instead of the ideal one.

No financial supports.

None.

The authors declare that they have no conflict of interest.

1. Ling G N (1992) A Revolution in the Physiology of the Living Cell, Krieger Pub Co, Malabar, Florida.
2. Ling G N (2001) Life at the Cell and Below-Cell Level: The Hidden History of a Fundamental Revolution in Biology, Pacific Press, New York.
3. Bagatolli L A, Mangiarotti A, Stock R P (2020) Cellular metabolism and colloids: Realistically linking physiology and biological physical chemistry. Prog Biophys Mol. Biol 162: 79-88.
4. Bagatolli L A, Stock R P (2021) Lipids, membranes, colloids and cells: a long view. BBA Biomembranes 1863(10): 183684.
5. Schneider M F (2021) Living systems approached from physical principles. Prog Biophys Mol Biol 162: 2-25.
6. Pollack G H (2001) Cells, Gels and the Engines of Life: A New, Unifying Approach to Cell Function, Ebner & Sons, Seattle, USA.
7. Pollack G H (2013) The Fourth Phase of Water: Beyond Solid, Liquid, and Vapor, Ebner & Sons, Seattle, USA.
8. Wnek G E, Costa A C S, Kozawa S K (2022) Bio-Mimicking, Electrical Excitability Phenomena Associated with Systhetic Macromoleculr Systems: A Brief Review with Connections to the Cytoskeleton and Membraneless Organelles. Frontiers in Molecular Neuroscience 15: 830892.
9. Funk R H W, Scholkmann F (2023) The significance of bioelectricity on all levels of organization of an organism. Part 1: From the subcellular level to cells. Prog Biophys Mol Biol 177: 185-201.
10. Ohki S (1976) Membrane Potential of Phospholipid Bilayer and Biological Membranes. Progress in Surface and Membrane Science 10: 117-252.
11. Ohki S, Aono O (1979) Membrane Potential of Squid Axons: Effect of Internal and External Ion Concentration. Japanese Journal of Physiology 29(4): 373-382.
12. Ling G N, Gerard R W (1950) External potassium and the membrane potential of single muscle fibers. Nature 165(4186):113.
13. Tamagawa H, Ikeda K (2018) Another interpretation of Goldman-Hodgkin-Katz equation based on the Ling's adsorption theory. Euro Biophys J 47(8): 869-879.
14. Katoh T, Inda Y, Nakajima S K, Ye R, Baba M, et al. (2010) Lithium/Air Batteries Using Li-Ion Conducting Glass Ceramics. ITE-IBA Letters New Technologies & Medicine 3: 327.
15. Tamagawa H, Nakahata T, Sugimori R, Delalande B, Mulembo T, et al. (2023) The Membrane Potential Has a Primary Key Equation. Acta Biotheoretica 71(3): 15.
16. Temsamani K R, Cheng K L (2001) Study of chloride adsorption on the Ag/AgCl electrode. Sens Actuat B: Chemical 76(1-3): 551-555.
17. Wright E M, Diamond J M (1968) Effects of pH and polyvalent cations on the selective permeability of gall-bladder epithelium to monovalent ions. Biochim Biophys Acta 163(1): 57-74.
18. Olschewski A, Olschewski H, Bräu B E, Hempelmann G, Vogel W, et al. (2001) Basic electrical properties of in situ endothelial cells of small pulmonary arteries during postnatal development. Am J Respir Cell Mol Biol 25(3): 285-90.
19. Uteshev VV (2010) Evaluation of Ca2+ permeability of nicotinic acetylcholine receptors in hypothalamic histaminergic neurons. Acta Biochim. Biophys Sin 42(1): 8-20.
20. Powell C L, Brown A W (2021) A classic experiment revisited: membrane permeability changes during the action potential. Adv Physiol Educ 45: 178.
21. Pollack G H, Figueroa X, Zhao Q (2009) Molecules, Water, and Radiant Energy: New Clues for the Origin of Life. Int J Mol Sci 10(4): 1419-1429.
22. Pollack G H (2013) The Fourth Phase of Water: Beyond Solid, Liquid, and Vapor. EDGESCIENCE 16: 14.
23. Pollack G H (2015) Cell electrical properties: reconsidering the origin of the electrical potential. Cell Biology International 39(3): 237-42.
24. Pollack G H (2017) Why Hydrogels Don’t Dribble Water. Gels 3(4): 43.
25. Kowacz M, Pollack G H (2019) Moving Water Droplets: The Role of Atmospheric CO2 and Incident Radiant Energy in Charge Separation at the Air-Water Interface. J Phys Chem B 123(51):11003-11013.
26. Kowacz M, Pollack G H (2020) Cells in New Light: Ion Concentration, Voltage, and Pressure Gradients across a Hydrogel Membrane. ACS Omega 5(33): 21024-21031.
27. Lewis G N, Randall M (1961) Thermodynamics, McGraw-Hill series in advanced chemistry, New York, USA.