 Research article
Research article
Advances in Theoretical Studies of Scintillators for Positron Emission Tomography Application
Salawu Omotayo Akande1*, Rabiatu Mahadi2 and Othmane Bouhali3
1Chemical and Biological Engineering department. Illinois Institute of Technology, Chicago, United States of America
2Physics Department, African University of Science and Technology, Abuja Nigeria
3Electrical and Computer Engineering, Texas AM University at Qatar
Salawu Omotayo Akande, Chemical and Biological Engineering department. Illinois Institute of Technology, Chicago, United States of America
Received Date:March 11, 2024; Published Date:August 08, 2024
Abstract
The application of scintillators in fields like health, security and nuclear science has been on the increase as a result of their efficiency in the detection of ionizing radiation. They are attractive due to their ability to convert high-energy rays to light. While efforts have channeled towards discovery, research and development of inorganic scintillator materials using experimental techniques, the importance of theoretical and computational methods in the investigation cannot be overemphasized. The theoretical/computational approach while most times support results obtained from experiment, has become tools for better understanding electronic properties, energy levels of defect states and emission centers in scintillators. In this review, we discuss the working principles of the scintillator and properties that are common for different ap-plications with emphasis on positron emission tomography. We identify issues related to the materials used in scintillators and review theoretical insights into these materials. Specifically, we focused on halide and oxide-based compounds and their derivatives. We also discuss how their respective properties make them attractive as scintillators and the development of theories that help better understand their properties on one hand and improve on the properties that need enhancement on the other hand.
Literature Review
Scintillation can be described as a type of luminescence that is caused by ionizing radiation [1]. When materials with this capability get hit by an incident radiation, the energy of the incident ionizing particles is absorbed and re-emitted as light. This phenomenon has been in use for a very long time and have made significant contribution to technology [2,3]. Since then, different materials have been discovered to have the scintillating properties [4,5]. Advancement in experimental physics has proven scintillation phenomenon can be found in organic and inorganic materials [4]. Inorganic scintillators are commonly employed as radiation detectors in different fields ranging from medical imaging to high-energy physics [6,7].
The importance of inorganic scintillators in medical imaging cannot be overemphasized. They find an application in Positron emission tomography (PET): A procedure that allows for imaging of molecular interactions and routes inside the human body [8]. It is an avenue for quantifying biochemical and physiological processes by applying radio-pharmaceuticals like 11C, 13N, 15O and 18F and by measuring the two 511 KeV photon emitted during the annihilation of the positron with an electron of the tissue [9-11].
Most applications of scintillators require similar properties. Desirable for different applications are properties like high light output, density and atomic number, short decay time without afterglow, radiation hardness, and ease of production [12]. The scarcity of materials having all (or most) of the aforementioned properties have resulted in the investigation of different classes of materials for application as scintillators. In this review, we describe the scintillation process including the properties of a scintillator and the working principle of a PET scanner. We further discussed material science issues related to scintillators and identified theoretical approaches used to investigate these issues and the different classes of materials considered. We also reviewed the different methods aimed at improving existing properties and design of new materials. Most of the factors discussed here are valid and applicable in other fields employing scintillators.
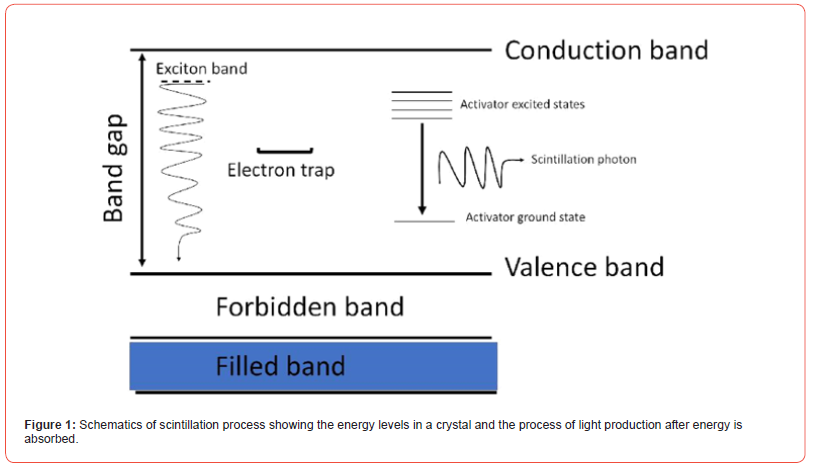
Scintillation Process
The scintillation process involves the absorbtion of ionization radiation which is in turn emitted as visible radiation. The process involves creation/transport of electron-hole pairs, the excitation of the luminescence centers and emission of light [6,13,14]. The process starts with a photon of intermediate energy, typically few hundred keV interacting with the lattice of a scintillator via a photoelectric effect and consequently creating hot electrons and holes (see Figure 1). Next, the primary electrons and holes enter a relaxation process and consequently numerous secondary electrons and holes are created. These secondary charge carriers dissipate energy as a result of interaction with other electrons or the lattice. Upon dissipating all their energies, the primary charge carriers migrate to the edges of conduction and valence band depending on their charge. The luminescence center acquires energy via capture of these electrons and holes with their recombination resulting in luminescent light. This process is very fast and takes few picoseconds. The presence of defects in the lattice can lead to trapping of the carriers thereby altering the performance of the crystal.
Principle of a PET Scanner
In nuclear medicine, radioisotopes are used for diagnosis, treatment or both. These radioisotopes are coupled to chemical compounds to form radio-pharmaceuticals tracers in order to target a specific biological or pathological process. Thus, these radiotracers are used to study biochemical processes in humans and animals. PET scanners are largely used in clinical nuclear medicine diagnosis.
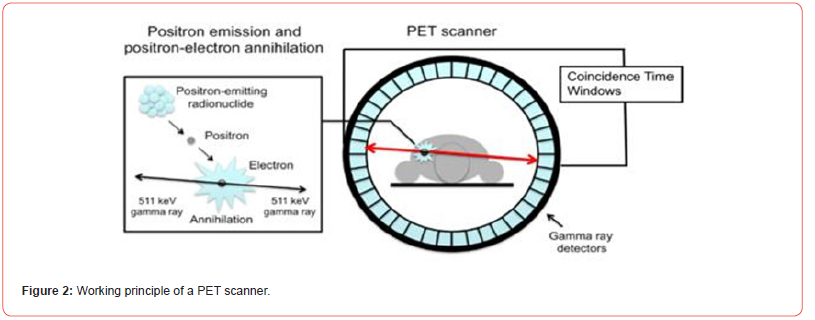
In PET, radiotracers with positron emitters such as 11C and 18F are injected into the body. The emitted positron loses its kinetic energy through successive collisions with the the surrounding environment and then annihilates with electrons present in the patient’s tissues. This annihilation process leads to the emission of two 511 keV photons traveling in opposite directions at 180 degrees (Figure 3). In PET scanner, a set of scintillation crystals is placed around the patient to form a cylindrical detector. These crystals are designed to detect the coincident 511 keV photons emitted during the annihilation process. The line formed by the two photons is called the Line of Response (LOR) and the total number of coincidence photons in each LOR is proportional to the radiotracer distribution. With an adequate reconstruction algorithm, the PET image can be reconstructed and used for diagnosis and prognosis. PET scanners have undergone significant development in the past two decades. A key element is the scintillation crystal which serves to convert the 511 keV photons to a visible light that can be detected and amplified by sophisticated circuitry. Additional elements have witnessed significant advances in computational power at different levels of the image reconstruction algorithm.
Properties of a Scintillator
An ideal scintillator is expected to possess a combination of
several physical, electronic and luminescence properties. Below we
present these properties that are intrinsic to the crystal material.
We will focus on the characteristics that impact the choice of
crystals for PET applications.
1. Light yield: This is a measure of the amount of light emitted per
unit of energy deposited in a crystal. It is directly related to the
intrinsic spatial resolution 15 and expressed in Photons/MeV.
It is the most important property of a scintillator. Possessing a
high light yield enables a scintillator to detect radiations with
even low intensity with a high signal-to-noise ratio.
2. Linearity: This property is linked to the energy resolution
of the scintillator [16-18]. It de-scribes the relation between
the energy of the incident particle and the light produced.
To demonstrate its importance, several studies have been
conducted to investigate the non-proportionality observed in
scintillating crystals.
3. Radiation stopping power: This is another important property
of a scintillator. It is the other property apart from light
yield upon which the intensity of the radioluminescence is
dependent on. It is described as the capability of the scintillator
to absorb incoming photons. It varies from one crystal to the
other since it depends on the density and effective atomic
number of the material. It serves as a good indication of how
efficient a scintillator is at absorbing incoming radiation [19].
4. Fast response time: This measures the rate at which a crystal
light after a photon is absorbed. This is the property that
determines the timing properties of the crystal [20,21]. This
property is particularly important for positron emission
tomography and other applications requiring high counting
-rate since a good coincidence timing ensures brief pulse of
the scintillation photon. To achieve this achieved a short decay
constant is essential.
5. Robustness and stability: presence of defects in materials,
intrinsic or those induced as a result of doping means a
stable material is desired as scintillator. More so, since the
scintillators will be exposed to radiation over a period of time,
it is essential that the scintillator is stable.
Depending on the application type, there are other properties that can be used to characterize a good scintillator including: spectral matching, radiation resistance for high radiation applications and low cost of growth.
Furthermore, over the years, developments in this field have enabled the introduction of a new concept in PET, that is the Time of Flight (TOF) which promises significant improvement in coincident photon acquisition and image quality [22]. In addition to the coincidence detection, TOF based detectors quantify the time between the interaction of the two photons within the respective crystals which improves the localization of the origin of the annihilation [23]. The implication of this is that the prior information on the exact localization of the positron emission point in the line of response (LOR) is improved thereby contributing to the rejection of events outside area of interest. Also, the noise in the reconstructed image is reduced while enhancing the image contrast. Additionally, advances in electronics and fast scintillation crystals have enabled the use of TOF-PET scanners with coincidence time resolution (CTR), enhancing significantly from 500–600 to 249 ps as recently announced by Siemens for their bio-graph vision scanner [24]. A time resolution of 10 ps give rise to an uncertainty of a mere 1.5 mm for a positron disintegration within the corresponding LOR. In addition, TOF-PET scanners require fast and efficient photosensors. Two main configurations exist based on scintillator crystal geometry, [25] namely the pixelated and the monolithic crystals. The former is the most extensive configuration on the TOF-PET scanners. For this crystal the coincidence time resolution is better than that obtained for the monolithic crystal. Although the monolithic crystals are getting popular for TOF-PET as a result of performance potential and cost. They are found to facilitate the determination of 3D in-formation of the -ray interaction within the crystal. The significance of this is that radial astigmatism at offcenter position can be corrected.
Materials Used as Scintillators in PET
Different kind of materials fulfilling the properties discussed above can be used as scintillator material for PET. Broadly speaking scintillators can be categorized as either organic or Inorganic Scintillators. Organic scintillators otherwise known as plastic scintillators comprises of a transparent host material (a plastic) doped with scintillating organic molecules (e.g. benzene). During operation, radiation is absorbed by the plastic via Compton effect as a result of its low density and the Z value of the organic molecules. As a result, this class of scintillators are mostly applied for detection of particles and fast neutrons. The other class of material, the inorganic scintillators are used for the detection of x and rays such as the 511 KeV ray used in PET owing to their high density and atomic number which results in better detection and efficiency. From our discussion of the requirements of a scintillator for PET, it is obvious that the inorganic scintillators are more suitable, hence we give a review of the development of this class of material.
Early PET scintillators were based on the use of Sodium Iodide (NaI (TI)) crystals [26]. Discovered in 1948, it became the scintillator of choice owing to its high light output. It is efficient in the conversion of deposited gamma ray to scintillation photons [27]. This advantage notwithstanding, it is found to have low detection efficiency due to its low density and low atomic number. It is also found to be highly hygroscopic. These lead to active research in finding a suitable material as scintillator in PET.
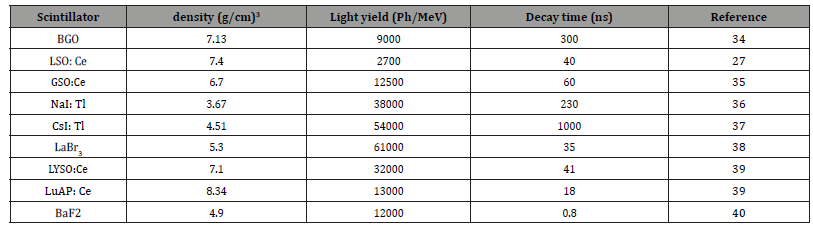
Around early 1970s, Bismuth germanium oxide (BGO) was put forward as a scintillator by Weber and co-workers [28]. Despite having a poorer light output than NaI(TI), it was reported to posses much higher detection efficiency due to its density. This has made it a popular candidate for radiation detection. It is still in use till date, however, its long decay constant implies that coincidence timing resolution is limited. The implication of this is that it cannot be a candidate for time-of-flight PET, since extremely short decay constant is desired if two detected photons are in “time coincidence” and belong to the same positron annihilation event. Candidate like BaF2 was found to have fast decay, high light output and non hygroscopic, hence was the material of choice in the 1980s. However, its low density and atomic number imply that a superior material is still desired. Table I shows the different scintillators and their properties.
The development of new scintillators has continued in the 1990s by the introduction of new crystals offering better time resolution, high density and high atomic numbers [22]. The first set of materials were discovered by Hofstadter. He worked on thallium-activated NaI and CsI, materials that are still widely used till date [29,30] Later, Ce-doped lutetium oxyorthosilicate, Lu2SiO5 (LSO) and derivatives such as LuxY2 xSiO5 were discovered [31,32]. They are known to have high light yield, high atomic number and high density, thereby making them a standard detector for PET applications [33].
The transport of the carriers in scintillators is an important factor that influences several important properties [41]. As can be deduced from analysis of the different scintillators, See Table 1, it is difficult to have a scintillator possessing all of the mentioned properties, as an ideal scintillator does not exist. Hence, scintillators with combination of most of the mentioned properties are desirable and this can vary from one application to the other. However,
Table 1:State of the art Scintillators and their properties.
It is expected that every scintillator for gamma-ray detection be efficient with respect to its stop-ping power, speed, luminosity and it must be affordable. There has been efforts to improve the desired properties in these scintillators. For example, there has been report of several mixed halide scintillators with better light yield and improved proportionality compared to conventional monovalent halide scintillators [42-44]. Although a fundamental understanding of such improvement is still elusive. While experiments can be conducted to probe these mate-rials, it is rather an expensive exercise, hence the use of computational/theoretical methods becomes necessary. A combination of computational and experimental effort is a sure way to improve existing scintillators and discover new ones.
Theoretical Studies of Materials for PET
In the investigation of materials for scintillation and for development of new scintillators, there is need for synergy between experiment and theoretical methods. In recent times, more and more efforts have been devoted to modeling and simulation of electronic properties like density of states and band structure of pristine material, position of energy levels and defect-related energy levels in the forbidden gap of pristine systems, which result in electron/ hole traps that affects the conversion and transport process of the scintillation mechanism. The experimental investigation of these properties is either expensive or not feasible. Moreover, not much computational work has been done with respect to gaining microscopic insight into the electronic basis of light output and linearity in materials used for PET. Studies 16 show that this depends on the energy density of charge carriers along ionization tracks. Investigation of this effect using experimental technique only yield qualitative insight, hence need for computational investigation of electronic and optical properties of these systems.
Furthermore, the mechanism of luminescence in scintillators can be due to self trapped excitons and transition between energy levels in pristine and doped scintillators respectively. Understanding the structural, electronic and optical properties of a material is necessary to shed more light into this kind of properties. Moreover, properties are coupled: knowledge of band structure is important in understanding optical process and similar properties in materials. Computational approach such as the density functional theory is an affordable means to calculate these properties and basis for further computational analysis.
Density Functional Theory
Key information related to structural, electronic, and optical properties, which are desired and offer better insight into the scintillation process are still not readily available for so many materials with scintillating capabilities. Therefore, an up-to-date methodology capable of effectively investigating these properties will go a long way in helping to improve existing materials and guide in discovery of new materials. The approach is based on the Kohn-Sham [45,46] formalism with the wave-functions of the electrons satisfying.

here p and Vxc are the charge density and exchange-correlation potential respectively. RI and Z represent the position and nuclear charges of the atoms respectively. The assumption while using this formalism is that the nucleus and core electrons are represented by an ionic pseudopotential in order that just the valence electrons are taken in to account in the evaluation of the wavefunction. The above equation is evaluated by minimizing the total energy via an iterative process until self consistency is realized.
Density functional theory [47] calculations offer important insight into the structural, chemical, electronic and optical properties of materials, and therefore can be a very useful tool in the understanding of existing materials, guide in the enhancement of properties of existing materials and search for superior materials. An understanding of the crystal structure and electronic properties is essential for the study of the defect chemistry especially those defects induced as a result of interaction with radiation. Typical properties needed for this investigation include the ground state energy of both the pristine system and defected system, the size of the band gap and the chemical potential of the vacant atom. In addition, there is a relationship between scintillation characteristics, defect and electronic structure. Specifically, quantity such as the band gap has been found to be inversely proportional to the number of charge carriers produced by the incident gamma ray [1,48] In addition, from electronic structure calculation, complex dielectric tensor can be calculated, a quantity that can be used to identify transitions responsible for optical absorption.
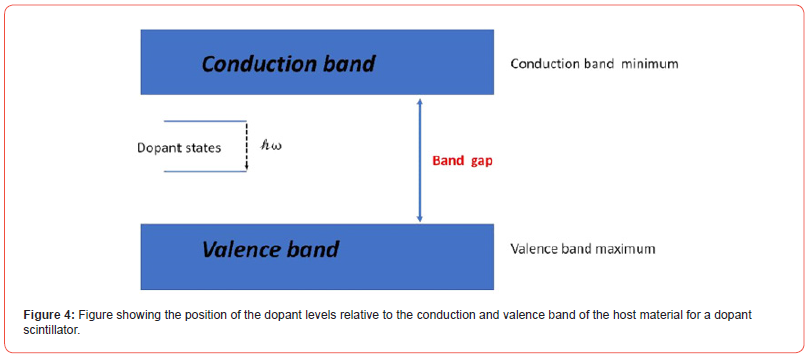
In view of the importance of this computational approach, there is a growing interest in ab initio modelling of the electronic properties of the host materials, energy-level positioning, and dopant systems. Although, electronic band structures of different materials have been made for years using the density functional theory and has provided insight into the electronic properties of such systems. The generalized gradient approximation [49] and local density approximation [50] have been successful in describing ground state properties of metals, insulators and semiconductors. The success of the DFT notwithstanding, it has been found in its standard form to underestimate the band gap of certain class of materials. Specifically, it fails to describe localized 3d and 4f states (dominant states determining band properties in these strongly correlated systems). Although development and research have provided a modification to the approach in the form of hybrid DFT [1]. This modification comprises the addition of a fraction of non-local Fock exchange to the functional. These approaches have been used successfully to describe the localized 3d and 4f states. Also, a quasiparticle self-consistent method, known as the DFT +U approach has been successfully employed to correctly reproduce the band gap value while also reproducing the level ordering and spacing of the 4f and 5d states in atoms like Ce [51]. This modification made the DFT based approach to be an excellent tool for determining the electronic structure of pristine, doped and excited states of different materials. Indeed, this approach has been employed to study oxide and halide based scintillators and other class of materials used as scintillators. Commonly used tools for this process include the Vienna ab-initio simulation package, (VASP), [52] Quantum espresso, [53] and WIEN2K [54]. For a review of different flavors of the DFT see reference [55] Choice of flavor used in calculating properties depends on the type of elements present in the compound and the information that is desired. The approach have been applied to studying pristine and doped materials. For doped systems, for example Ce doped scintillators, an indicator of suitability of the material is based on the calculation of the Ce 5d and 4f levels relative to the bands of the host material (see Figure 5) [56].
In an attempt to identify and design materials that are resistant to radiation-induced defects, there is need for novel and systematic strategies. One strategy that has been applied is the band engineering, aimed at eliminating radiation induced defect states in scintillators [51].
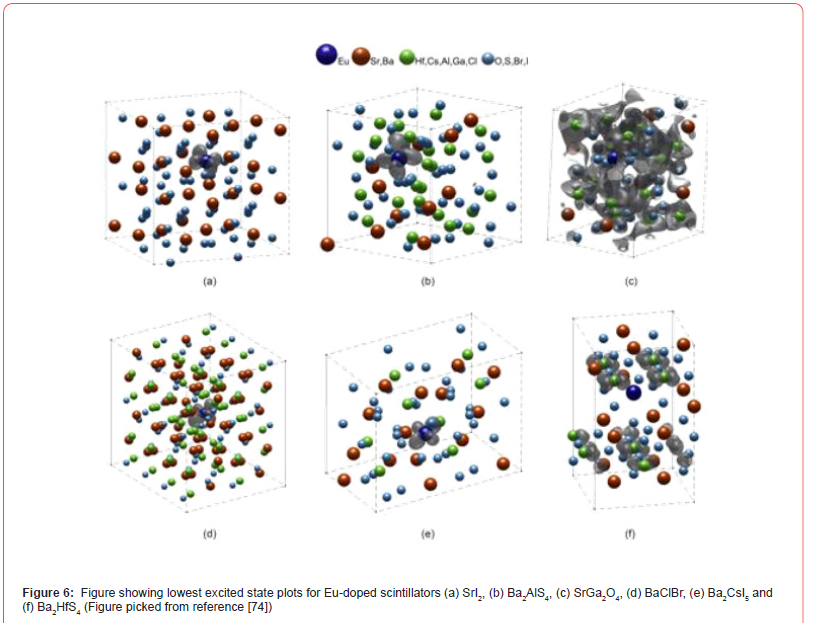
Liu and coworkers explored this approach to Ce doped LuAlO3. The investigation involves using hybrid DFT to calculate defect energetics in the material [51]. The research showed that all the radiation induced defect in the material have shallow defect states except O vacancy, see Figure 6. These states are far away from the dopant induced states thereby encouraging the application of band engineering to eliminate effect of the defect states on carrier traps and consequently improving scintillation efficiency.
Monte-Carlo Method
A distinguishing route in theoretical calculation of scintillation efficiency for a while now has been an active simulation of the initial processes of the ionizing particle track development in both halide and oxide based scintillator materials [57]. Monte Carlo (MC) simulations approach allow deeper analysis of the process of successive generation and propagation of electron-hole pairs. It also allows for the analysis of all the subsequent processes up to the scintillation photons emission. Using this approach, optical photon transport can be studied, as the inclusion of optical transport affect some performance parameters of these detector models [57]. One popular tool for MC simulation is the Geant4, [58] a toolkit for simulating the passage of particles through matter. An object-oriented based code, implemented in the C++ programming language, It was constructed to explore the physics models employed to handle complex structures, and to enable its easy usage in different fields. Specifically, the scintillation properties of halides like CsI(Na), CsI(Tl) and LaBr3 were simulated using GEANT4. The objective of the calculation was to identify materials best suited for monitoring environmental radiation [59] Efforts have also been channeled towards understanding the formation of spatial distribution of charge carriers due to thermalization. The thermalization stage in the operation of the scintillator is determined by the interaction of hot electrons/holes with kinetic energy below the forbidden band gap value with photons. Kinetic Monte-Carlo have been used to describe these interactions and recombination of charge carriers [57] This approach apart from offering fundamental insight, also investigate the root of non proportionality in scintillators.
Similarly, MC model has been used in the design and profiling of composite scintillators. The monitoring of every scintillation photon in the simulation lead to the generation of decay curves and consequently used to build pulse height spectra. This process have been applied successfully to detect efficiency, spatial resolutions and analyzing powers of a time-of-flight (TOF) PET detector systems such as Cerium doped Lutetium Oxyorthosilicate (Lu2SiO5: Ce, LSO), Barium Fluoride (BaF2) and Cerium doped Lanthanum tri- Bromide (LaBr3) scintillation crystals.
We provide progress made via theoretical methods for each class of material below.
Halide-Based Scintillators
Halide perovskites have been reported to be excellent luminescent material because of re-ported impeccable photoluminescence quantum yield and ease of fabrication [60]. The latter advantage is particularly important owing to the high cost incurred with commercial scintillators. The commercial scintillators are also known to have fixed emission wavelengths which limits their functionality with substrates and detectors [61]. This has made developing new scintillators with increased functionality and performance of paramount interest especially in the field of medical imaging. Halide perovskites have high atomic number and contain heavy elements like as Pb, Br and I atom. They are known to possess good ionizing radiation absorption ability, high stopping power, low detection limit and polychromatic radioluminescence, a characteristic enabling radiation detection [62?]. All of these properties have made halide perovskites to be a candidate for the most promising scintillators.
Despite increased research and progress over the last couple of years in the usage of halide perovskite as scintillators, there still exist challenges hampering their wide spread application. The reluctance in its wide usage is unconnected to issues with their stability, [63] self-absorption effect, [60] hygroscopy and toxicity. The stability of materials often has direct impact on their performance during operation. The high sensitivity of the material to environmental conditions like heat and humidity, and ability of defects to form easily when exposed to radiation affect the stability of the material. The self-absorption phenomenon is another factor that limits the halide perovskites. It involves the re-absorption of photons previously emitted by a crystal by itself. This phenomenon affects the light yield and consequently coupling efficiency of the scintillator. Also, the presence of Pb in most halide-based perovskites have hampered their widespread application due to its toxic nature.
Efforts made to address the issues mentioned include dimensionality and compositional engineering, [64] improved growth methods, [65] and passivation. A joint multidisciplinary research is required to characterize effectively the issues, understand the characteristics of the materials and improve performance. Computational methods have been successfully used to tackle some of the issues and more insight have been provided especially in areas where experiments are either expensive or cumbersome [62]. Specifically, efforts have been made to characterize and discover lead- free halide perovskites [60]. These efforts involve doping the scintillators with other elements while maintaining impeccable optoelectronic performance.
Density functional theory has been employed to study halide based scintillators. Sub-classes of halide-based scintillators studied include alkali-based halides, rare-earth and different dopant variants of these materials, see Figure 6 [66,67]. For a while alkali halide-based scintillators have been model systems and has paved ways for the fundamental understand of scintillator technology. Insight from studies of alkali halides have provided detailed understanding of point defects. Alongside point defect-related traps, the mechanisms of charge or exciton self-trapping are areas of paramount importance in scintillator physics. Recent research have reported several novel halide-based scintillators with excellent scintillation properties [68]. Specifically, the structural, electronic, and optical properties of CeX3 (X = Cl, Br) within the generalized gradient approximation. The lattice parameters and optical properties calculated are in good agreement with the experimental data [69]. The investigation further obtained the energy band structures and density of states and optical properties. Theoretical methods have also been employed in the study of defect in halides namely in calculating formation energies of iodide vacancy in SrI2 for different charge states [70]. The work successfully investigated optical trap depth, absorption transitions and thermal trap depth of the luminescence centers. Other theoretical investigations examined lanthanum-based halides like LaBr3 and LaCl3 [71]. These offer energy resolution of 2.6- 3.3% at 662 keV, however growing them is challenging. Efforts have also been made to investigate Eu-doped halides like BaI2, BaBr2, SrI2, SrBr2, CaI2 and mixtures of these compounds because of their scintillation properties. This investigation identified strontium iodide as readily growable.
They offer high light yield and are capable of high energy resolution. Other investigations of scintillation of alkaline earth halides have reported about 100,000 Photons/MeV, for CaI2(Eu) and its structure (it has hexagonal crystal structure with pronounced basal cleavage) makes it difficult to grow. Alternatively, BaI2(Eu) and BaBr2(Eu) which are reported as orthorhombic crystals are much easier to grow, although their light yields are only about 35,000 Ph/MeV.
Furthermore, DFT calculations were performed to study ns2 (6p and 5p ions with outer electronic configurations of ns2) ions in halides, [72] revealing that the positions of the activator levels relative to the valence and conduction band edges depends strongly the hybridization of the activator-halogen hybridization strength. A similar approach was employed to distinguish prospective Eu2+ host materials considered as scintillators. The research was designed to help in the discovery of new materials by prioritizing key properties and to relate theoretically obtained parameters to properties obtained experimentally. This approach followed a previously established approach used for Ce-doped system [73] and successively produced a list of candidate materials as scintillators (see Figure 4)
A combination of DFT and MC have been successfully used to model the non-proportionality of halide scintillators. These efforts investigated the origin and ways of inhibiting this effect that have been found to degrade energy resolution [65]. These researches focused on the electron and hole thermalization processes within the conduction and valence bands [75-77] These was done by analyzing the thermalization and recombination of the complex relaxation process which depends on energy and spatial scales of the process. It was revealed that scintillators with complex structures show short thermalization length hence higher chance of recombination of electros and holes. This leads to a good nonproportionality if the mobility of the thermalized excitons is high since the transfer of energy to activator becomes efficient [77].
Oxide-based Scintillators
Around the same time CsI:Ti was discovered, CdWO4 was reported as a single crystal scintillator [79] Since then, so many other oxide based scintillators have been reported. Among them garnets like Y3Al5 O12 (YAG) [80] and pyroslilicates like the Lu2SiO5 [81] and other perovskite type oxides. All of these compounds are highly rated as candidates for scintillators due to their high density and fast scintillation response Theoretical methods like the DFT have been successfully employed to study this class of material. The structural, electronic, optical and defect properties of these materials have been extensively discussed. Investigation in these materials also include the effect of doping with rare earth ions. The spin and parity allowed 5d-4f transitions permit rapid scintillation response in these materials. Similar approach was employed to investigate the band structure of yttrium-based materials like the YAG, YAP and YPS. It was found that the top of the valence band is primarily occupied by the O p states while the 4d orbitals dominate the conduction band. This observation assisted in understanding how defect is characterized in these materials. Similar investigation in bismuth germanate and their derivatives revealed that a major part of the radiation energy is absorbed by O p electrons, (which dominates the valence band) and transferred to the Bi p electrons.
Owing to the fact that Lutetium Yttrium Orthosilicate has good scintillating properties and also cheap to grow, it will be our model system for investigation. Moreover, most of the scintillating system crystallizes in perovskite structure, hence inferences made from this study can easily be replicated in other similar structures. Not that the properties of this material have been well studied experimentally and data are available to this effect. However, the properties of the variants obtained as a result of change in the stoichiometry of the lanthanide and yttrium, as well as the impact of doping the “A” and “B” site still remain largely unexplored.
Among oxide-based scintillators garnet materials have been a subject of intense research due to their excellent performance. Specifically, crystals like YAG and LuAG [82] have been extensively studied because they are relatively easy to grow. It has been recently discovered [83] that multi-component garnets like gadolinum gallium aluminium garnet (GdGaAl2O12:Ce, GGAG) posses a much higher light yield, about 60,000 ph/MeV. This was attributed to a decrease in the concentration of traps in the conduction band. This prevents the ionization-induced quenching of the excited 5d level of the Ce3+ activator ion.
Other researches have shown that a possible route for the improvement in properties is the doping of host materials(oxidebased) with tetravalent ions like Ce4+. They opined that, this is achieved by allowing fast radioactive recombination such that they efficiently compete with electron traps for the capturing of electrons from the conduction band. The ions were found to be rapidly reduced to Ce3+ ions by this process and consequently cerium emitted. This result has inspired different co-doping routes designed to stabilize the 4+ ionization state of cerium in several systems considered for this application. Similarly, the use of divalent dopants such as Ca2+ or Mg2+ have shown to be useful in reducing the decay time of systems like GGAG. In the past, several Ce3+ doped compounds have emerged that do gamma ray spectroscopy at high rates. Lutetium-based materials are found to yield particularly good properties. An example is the lutetium orthosilicate (LSO or Lu2SiO5:Ce), which has been reported to have a light output of about 25,000 photons/MeV, a decay time of 40 ns, and a density of about 7.4 g/cc. This feature that makes it suitable for positron emission tomography (PET)
Challenges with PET Scintillators
There are still many unresolved issues associated with practical application of scintillators despite its significance. Here, we present some the unresolved issues and explain the most recent efforts channeled towards solving them.
Positive Hysteresis
Positive hysteresis also known as radiation drift can be described as an enhancement of the scintillation light yield which is observed after a large dosage of radiation exposure. Although not a common phenomenon, it is reported for materials such as materials including Pr-doped Lu2Si2O7 (LPS)) Tl-doped CsI) Ce-doped and Ce/ Zr co-doped Gd2SiO5 (GSO)) Ce-doped Gd3(Al,Ga)5O12 (Ce:GAGG)) Tb-doped SiO2 glass and Ce/Nd co-doped YPO4. From a practical stand point, there is a need to suppress or minimize positive hysteresis, this becomes necessary since it is capable of causing some ghosts in a radiation image [84]. From a physics point of view, the root of positive hysteresis is unclear and a topic of discussion, although it is considered that carrier traps and the generation of new excitation bands above the band gap energy are important factors in the discussion of positive hysteresis. From practical point of view, read out softwares can be adopted to suppress or correct positive hysterisis. Worthy of note is that previously, two different measurements (the pulse-height spectrum and radio luminescence) were considered to determine the scintillation light yield involved in this menace.
Optical loss in Scintillators
One major challenge which perovskite-based scintillators face is its transparency which is related to its light output. Although, several kind of materials including bulk single crystals, glasses, nano-particles and organic polymers have been studied as scintillators, single crystals remain the most efficient class of material with the capability of competing with semiconductors for high energy gamma ray detection. The discovery of new scintillator materials have been slow owing to the number of criteria that a material have to satisfy in order to be considered a good scintillator. These days, in the field of scintillator research like in most material science research, new materials have been continually identified by both rapid fabrication methods and high-throughput simulation. Despite improvement in the efficiency of experimental screening methods, the discovery of new materials solely by experiment is still very limited. In the last ten years, over 100 compounds have been considered, however only a small fraction have been tested for scintillation. This limitation further underlines the potential impact of computational material design in discovery of new scintillators. Approaches such as data mining, molecular dynamics, density functional theory and thermodynamic computing have the potential to speed up the search for a new scintillator.
Enhancing the Efficiency of a Scintillator
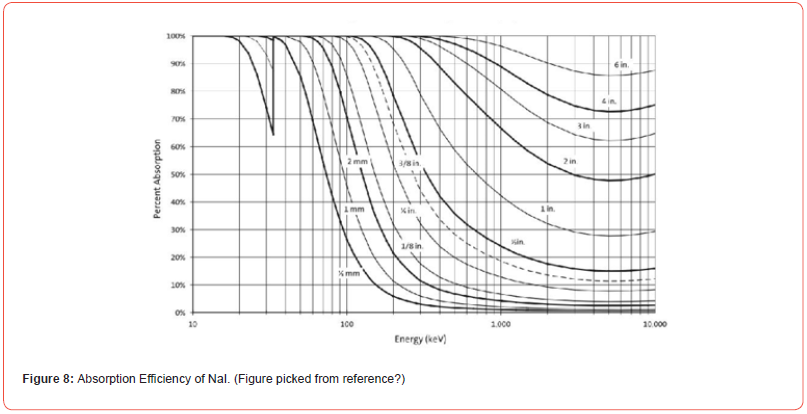
The increase in demand for a better detection performance, reduction in weight, power consumption and cost has motivated a lot of research in the materials for scintillators. As mentioned above, several factors make a scintillator to be efficient and there is no ideal scintillator yet; No single scintillator have all the mentioned properties, hence there is need to improve the overall efficiency of the scintillator. Factors such as the time resolution, detection thickness, absorption coefficient are indicators that determine the efficiency of a scintillator and the indices on these factors determine the suitability of the scintillator for a particular application. The interdependence of the amount of radiation emitted from a source and the amount measured in a detector can be quantified by the detector counting efficiency. For some applications, it is important to quantify photopeak events generated by a detector. This can be done, by measuring the absorption efficiency of the scintillator which comprises of Compton edge, single and double escape peaks and other compton events,59 see Figure 7.Figure 8
The detection efficiency of a scintillator is dependent on its ability to attenuate photons and is expressed in terms of the mass attenuation coefficient. It is required that to attain the best energy resolution (defined as the full width at half maximum—FWHM), a scintillator should posses high optical yield. This can be quantified as the number of optical photons that are emitted per energy deposited into the crystal volume by the intercepted gamma-ray photon. Since the energy of the incident gamma-ray and the mass attenuation coefficient are directly related l to the density and the atomic (Z) number of the material, detectors composed of Cs (Z = 55) and La (Z = 57) have greater radiation “stopping power” than those of lower densities and Z-numbers, with the detector efficiencies of Gd (Z = 64). This fact is used in selection of materials. In the same vein, in order to optimize the optical photon yield, the peak emission wavelength of the scintillator should be in tandem with the spectral quantum efficiency of the light sensor [59]. Furthermore, higher light output can be achieved in materials with small band gap. This is because they are known to offer more ionization per unit energy and more photons can be emitted [85].
A review of theoretical investigations reveal that electronic scattering and electron-phonon thermalization are two factors that influence scintillator efficiency. The latter is related to the decrease in germinate pair concentration and to some extent luminescence loss. A decrease in the thermalization length is one avenue to forestall these and can be achieved by crystal doping. These have been shown to lead to higher light output in halide, oxide and sulfur-based scintillators. A combination of these theoretical findings and experimental data indicate that scintillation efficiency can be improved.
One way proposed for thermalization length decrease is the scintillation crystal doping [86, 87]. Dopants change the electronic properties of the host materials and consequently affects the light yield. The introduction of dopant might generate oxygen interstitials which in turn reduce the oxygen vacancy concentration through a Frenkel-pair recombination. Reducing the oxygen vacancy concentration is one way to promote scintillation as this lead to trapping of electrons in the system. Another benefit of doping the host material is that, it can act as a way of increasing the density of the material.
The search for multi element compounds out of a large combinatorial space is non-trivial. This is especially take into challenging for doped bulk gamma detector materials, where one has to account different concentrations of dopant. This large possibility is a huge challenge and slowed down the development of the next generation of scintillator materials. This is despite an increasing theoretical understanding of the material/performance relationship, the process is predominantly developed through a time-consuming and cumbersome approach. Advancement in computational method has offered methodologies such as data mining and artificial intelligence in the search for viable dopants and mapping out properties for optimal performance in scintilators. For instance, in relatively simple binary systems, computational techniques are helpful in unraveling the complex interplay between composition, energy flow, and material performance. While the use of combinatorial optimization approach in order to account for large parameter space has been useful for thin film and powder forms material development, little success have been recorded when applied to bulk material and further investigation is required in these area.
Future Trends and Recommendation and Conclusion
There are on-going investigations both experimentally and theoretically to discover new scintillators especially for PET, this is because the performance of tomography is strongly linked to the capabilities of a scintillator. Although most of the research is centered around materials with high atomic number and high density, some of the studies are focused on finding materials with short decay constants. Interestingly, most of these efforts rely heavily on computational methods like first principles studies, artificial intelligence, data mining etc. [16, 86, 87] These approaches are on one hand improve understanding of the fundamentals and underlying physics of scintillation, and on the other hand help to predict the properties of a large pool of potential scintillators without having to synthesize them in the laboratory.
The research on scintillating materials over the years have evolved and have taken on a multi-disciplinary dimension. A synergy as been built across experimental and theoretical approaches with each field working towards improving existing materials and discovery of new materials. These efforts are based on the ever dynamic demands in field applying scintillators. Theoretical methods have shown to be cheaper alternative to experiment especially in the search for new materials owing to the relative low cost of conducting research using this method. This effort have been boosted by advancement in theoretical capabilities with the rise in popularity of multi-scale modelling and data mining to material physics research. Experimental data confirmed theoretical findings on light output increase and role of cation/anion doping in oxides, halides, and sulfur-based scintillators.
Acknowledgment
None.
Conflict of interest
None.
References
- Jin Kim H (2015) Computational design of new scintillator chemistries and defect struc-tures.
- Moon R J (1948) Inorganic crystals for the detection of high energy particles and quanta. Physical Review 73: 1210.
- Lecoq P (2007) Inorganic Scintillators for Detector Systems [electronic Resource]: Physical Principles and Crystal Engineering.
- Bell P R (1948) The use of anthracene as a scintillation counter. Physical Review 73: 1405.
- Schorr M G, Torney F L (1950) Solid non-crystalline scintillation phosphors. Physical Review 80: 474.
- Rodnyi P A (1997) Physical processes in inorganic scintillators; CRC press 14.
- Prange M, Wu D, Xie Y, Campbell L W, Gao F, et al. (2014) Radiation response of inorganic scintillators: Insights from Monte Carlo simulations. Hard X-Ray, Gamma-Ray, and Neutron Detector Physics XVI p. 92130L.
- Phelps M E (2000) Positron emission tomography provides molecular imaging of biological processes. Proceedings of the National Academy of Sciences 97(16): 9226-9233.
- Peng H, S Levin C (2010) Recent developments in PET instrumentation. Current pharma-ceutical biotechnology 11(6): 555-571.
- DeGrado T R, Baldwin S W, Wang S, Orr M D, Liao R P, et al. (2001) Synthesis and evaluation of 18F-labeled choline analogs as oncologic PET tracers. Journal of Nuclear Medicine 42(12): 1805-1814.
- Eriksson B, Örlefors H, Öberg K, Sundin A, Bergström M, et al. (2005) De-velopments in PET for the detection of endocrine tumours. Best Practice & Research Clinical Endocrinology & Metabolism 19(2): 311-324.
- Blasse G (1994) Scintillator materials. Chemistry of Materials 6: 1465-1475.
- Rodnyi P A (1995) Physical Processes in Inorganic Scnitillators; CRC.
- van’t Spijker J (1999) Luminescence and scintillation of Ce (3+) doped inorganic materials for gamma-ray detection.
- Lecoq P, Auffray E, Knapitsch A (2013) How photonic crystals can improve the timing resolution of scintillators. IEEE Transactions on Nuclear Science 60: 1653-
- Jaffe J E, Jordan D V, Peurrung A J (2007) Energy nonlinearity in radiation detec-tion materials: Causes and consequences. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 570: 72-
- Moses W W, Payne S, Choong WS, Hull G, Reutter B W (2008) Scintillator non-proportionality: Present understanding and future challenges. IEEE Transactions on Nuclear Science 55: 1049-1053.
- Bizarri G, Moses W W, Singh J, Vasil’Ev A, Williams R, et al. (2009) An analytical model of nonproportional scintillator light yield in terms of recombination rates. Journal of Applied Physics 105: 044507.
- Saha G B (2015) Basics of PET imaging: physics, chemistry, and regulations.
- Sæterstøl J (2010) Characterization of Scintillation Crystals for Positron Emission Tomogra-phy.
- Ota R, Nakajima K, Ogawa I, Tamagawa Y, Shimoi H, et al. (2019) Coincidence time resolution of 30 ps FWHM using a pair of Cherenkov-radiator-integrated MCP-PMTs. Physics in Medicine & Biology 64(7): 07LT01.
- Surti S, Kuhn A, Werner ME, Perkins A E, Kolthammer J, et al. (2007) Perfor-mance of Philips Gemini TF PET/CT scanner with special consideration for its time-of-flight imaging capabilities. Journal of Nuclear Medicine 48(3): 471-480.
- Conti M (2009) State of the art and challenges of time of flight PET. Physica Medica 25(1): 1-11.
- Beyer T, Lassen M L, Boellaard R, Delso G, Yaqub M, et al. (2016) Investigating the state-of-the-art in whole-body MR-based attenuation correction: an intra-individual, inter-system, inventory study on three clinical PET/MR systems. Mag-netic Resonance Materials in Physics, Biology and Medicine 29(1): 75-87.
- Sánchez Gonzalo D (2021) Optimized PET module for both pixelated and monolithic scintil-lator crystals.
- Hofstadter R (1948) Alkali halide scintillation counters. Physical Review 74: 100.
- Melcher C L (2000) Scintillation crystals for PET. Journal of Nuclear Medicine 41(6): 1051-1055.
- Weber M J, Monchamp R R (1973) Luminescence of Bi4 Ge3 O12: Spectral and decay properties. Journal of Applied Physics 44: 5495-5499.
- Hofstadter R (1949) The detection of gamma-rays with thallium-activated sodium iodide crys-tals. Physical Review 75: 796.
- Weber M J (2002) Inorganic scintillators: today and tomorrow. Journal of Luminescence 100: 35-45.
- Wang Y, van Loef E, Rhodes W H, Glodo J, Brecher C, et al. (2009) Optical Ceramic Scintillator for PET. IEEE Transactions on Nuclear Science 56: 887-891.
- Nassalski A, Kapusta M, Batsch T, Wolski D, Mockel D, et al. (2005) Comparative study of scintillators for PET/CT detectors. IEEE Nuclear Science Symposium Conference Record pp. 2823-2829.
- Herzog H, Tellmann L, Hocke C, Pietrzyk U, Casey M E, et al. (2004) NEMA NU2-2001 guided performance evaluation of four Siemens ECAT PET scanners. IEEE Transactions on Nuclear Science 51: 2662-2669.
- Cho Z, Farukhi M (1997) Bismuth germanate as a potential scintillation detector in positron cameras. Journal of nuclear medicine 18(8): 840-844.
- Valais I, Michail C, David S, Nomicos C, Panayiotakis G, et al. (2008) A com-parative study of the luminescence properties of LYSO: Ce, LSO: Ce, GSO: Ce and BGO single crystal scintillators for use in medical X-ray imaging. Physica Medica 24: 122-125.
- Moszyński M, Zalipska J, Balcerzyk M, Kapusta M, Mengesha W, et al. (2002) Intrinsic energy resolution of NaI (Tl). Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 484: 259-269.
- Nagarkar V, Gupta T, Miller S, Klugerman Y, Squillante M, et al. (1998) Struc-tured CsI (Tl) scintillators for X-ray imaging applications. IEEE transactions on nuclear science 45: 492-496.
- Van Loef E, Dorenbos P, Van Eijk C, Krämer K, Güdel H U, et al. (2001) High-energy-resolution scintillator: Ce 3+ activated LaBr 3. Applied physics letters 79: 1573-1575.
- Chewpraditkul W, Swiderski L, Moszynski M, Szczesniak T, Syntfeld-Kazuch A, et al. (2009) Scintillation properties of LuAG: Ce, YAG: Ce and LYSO: Ce crystals for gamma-ray detection. IEEE Transactions on Nuclear Science 56: 3800-3805.
- Schotanus P, Van Eijk C, Hollander R, Pijpelink J (1985) Temperature dependence of BaF2 scintillation light yield. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 238: 564-565.
- Huang H, Li Q, Lu X, Qian Y, Wu Y, et al. (2016) Role of hot electron transport in scintillators: A theoretical study. physica status solidi (RRL)–Rapid Research Letters 10: 762-768.
- Fang C, Biswas K (2016) Quaternary iodides A (BaSr) I5: Eu2+ (A= K, Cs) as scintillators for radiation detection. The Journal of Physical Chemistry C 120: 1225-1236.
- Stand L, Zhuravleva M, Camarda G, Lindsey A, Johnson J, (2016) Exploring growth conditions and Eu2+ concentration effects for KSr2I5: Eu scintillator crystals. Journal of Crystal Growth 439: 93-
- Yan Z, Shalapska T, Bourret E (2016) Czochralski growth of the mixed halides BaBrCl and BaBrCl: Eu. Journal of Crystal Growth 435: 42-45.
- Hohenberg P, Kohn W (1964) Inhomogeneous electron gas. Physical review 136: B864.
- Kohn W, Sham L J (1965) Self-consistent equations including exchange and correlation eff Physical review 140: A1133.
- Bickelhaupt F M, Baerends E J (2000) Kohn-Sham density functional theory: predicting and understanding chemistry. Reviews in computational chemistry 15: 1-86.
- Derenzo S, Weber M, Bourret-Courchesne E, Klintenberg M (2003) The quest for the ideal inorganic scintillator. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 505: 111-117.
- Grimme S (2006) Semiempirical GGA-type density functional constructed with a long-range dispersion correction. Journal of computational chemistry 27: 1787-1799.
- Parr R G (1980) Horizons of quantum chemistry pp. 5-15.
- Liu X Y, Pilania G, Talapatra A A, Stanek C R, Uberuaga B P, et al. (2020) Band-Edge Engineering To Eliminate Radiation-Induced Defect States in Perovskite Scintillators. ACS Applied Materials & Interfaces 12(41): 46296-46305.
- Hafner J (2008) Ab-initio simulations of materials using VASP: Density-functional theory and beyond. Journal of computational chemistry 29(13): 2044-2078.
- Giannozzi P, Baroni S, Bonini N, Calandra M, Car R, et al. (2009) QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. Journal of physics: Condensed matter 21: 395502.
- Blaha P, Schwarz K, Madsen G K, Kvasnicka D, Luitz J, et al. (2001) WIEN2k, An augmented plane wave plus local orbitals program for calculating crystal properties. Vienna University of Technology, Vienna p. 243.
- Payne M C, Teter M P, Allan D C, Arias T, Joannopoulos a J, et al. (1992) Iterative min-imization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients. Reviews of modern physics 64: 1045.
- Canning A, Boutchko R, Chaudhry A, Derenzo S E (2009) First-principles studies and predictions of scintillation in Ce-doped materials. IEEE Transactions on Nuclear Science 56: 944-948.
- Gektin A V, Belsky A N, Vasilev A N (2013) Scintillation efficiency improvement by mixed crystal use. IEEE Transactions on Nuclear Science 61: 262-
- Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, et al. (2003) GEANT4—a simulation toolkit. Nuclear instruments and methods in physics research section A: Accelerators, Spectrometers, De-tectors and Associated Equipment 506(3): 250-303.
- Lowdon M, Martin P G, Hubbard M W, Taggart M P, Connor D T, et al. (2019) Evaluation of scintillator detection materials for applica-tion within airborne environmental radiation monitoring. Sensors 19(18): 3828.
- Wu Y, Ren G, Meng F, Chen X, Ding D, et al. (2014) Effects of Bi3+ codoping on the optical and scintillation properties of CsI: Tl single crystals. physica status solidi 211: 2586-2591.
- Moseley O D, Doherty T, Parmee R, Anaya M, Stranks SD, et al. (2021) Halide Perovskites Scintillators: Unique Promise and Current Limitations. Journal of Materials Chemistry.
- Zhou F, Li Z, Lan W, Wang Q, Ding L, et al. (2020) Halide Perovskite, a Potential Scintillator for X-Ray Detection. Small Methods 4: 2000506.
- Li Z, Zhou F, Wang Q, Ding L, Jin Z, et al. (2020) Approaches for thermodynamically stabilized CsPbI3 solar cells. Nano Energy 71: 104634.
- Huang Y, Qiao L, Jiang Y, He T, Long R, et al. (2019) A-site Cation Engineering for Highly Efficient MAPbI3 Single-Crystal X-ray Detector. Angewandte Chemie International Edition 58(49): 17834-
- Matt G J, Levchuk I, Knüttel J, Dallmann J, Osvet A, et al. (2020) Sensitive Direct Converting X-Ray Detectors Utilizing Crystalline CsPbBr3 Perovskite Films Fabricated via Scalable Melt Processing. Advanced Materials Interfaces 7: 1901575.
- Kumar P, Vedeshwar A G (2015) DFT calculations of structural, electronic, optical and elas-tic properties of scintillator materials BaCl2 and BaBr2. Journal of Physics D: Applied Physics 48: 105301.
- Myasnikova A, Vasilkovskiy A, Bogdanov A, Shendrik R Y, Kaneva E, et al. (2017) Ab initio study of alkaline-earth halide scintillators doped with Eu 2+ ions. Bulletin of the Russian Academy of Sciences: Physics 81: 1086-1089.
- Vistovskyy V, Zhyshkovych A, Chornodolskyy Y M, Myagkota O, Gloskovskii A, (2013) Self-trapped exciton and core-valence luminescence in BaF2 Journal of Applied Physics 114: 194306.
- Li C, Wang B, Wang R, Wang H (2007) First-principles studies on the electronic and optical properties of CeCl3 and CeBr3. Solid state communications 144: 220-224.
- Li Q, Williams R, Åberg D (2013) First principles calculations and experiment predictions for iodine vacancy centers in SrI2. physica status solidi (b) 250: 233-243.
- Cherepy N, Sturm B, Drury O B, Hurst T, Sheets S, et al. (2009) SrI [sub] 2 [/sub] scintillator for gamma ray spectroscopy. Hard X-Ray, Gamma-Ray, and Neutron Detector Physics XI p. 74490F.
- Du MH (2014) Chemical trends of electronic and optical properties of ns 2 ions in halides. Journal of Materials Chemistry C 2: 4784-4791.
- Canning A, Chaudhry A, Boutchko R, Grønbech-Jensen N (2011) First-principles study of luminescence in Ce-doped inorganic scintillators. Physical Review B 83: 125115.
- Chaudhry A, Boutchko R, Chourou S, Zhang G, Grønbech-Jensen N, et al. (2014) First-principles study of luminescence in Eu 2+-doped inorganic scintillators. Physical Review B 89: 155105.
- Belsky A, Ivanovskikh K, Vasilev A, Joubert MF, Dujardin C (2013) Estimation of the electron thermalization length in ionic materials. The Journal of Physical Chemistry Letters 4: 3534-3538.
- Ucer K, Bizarri G, Burger A, Gektin A, Trefilova L, et al. (2014) Electron ther-malization and trapping rates in pure and doped alkali and alkaline-earth iodide crystals studied by picosecond optical absorption. Physical Review B 89: 165112.
- Vasilev A N, Gektin AV (2013) Multiscale approach to estimation of scintillation charac-teristics. IEEE Transactions on Nuclear Science 61: 235-245.
- Lalic M, Souza S (2008) The first-principles study of electronic and optical properties of BGO and BSO scintillators. Optical Materials 30: 1189-1192.
- Lotem H, Burshtein Z (1987) Method for complete determination of a refractive-index tensor by bireflectance: application to CdWO4. Optics letters 12(8): 561-563.
- Weber M (1973) Nonradiative decay from 5d states of rare earths in crystals. Solid State Communications 12: 741-744.
- Melcher C, Schweitzer J (1992) A promising new scintillator: cerium-doped lutetium oxy-orthosilicate. Nuclear Instruments and Methods in Physics Research Section A: Acceler-ators, Spectrometers, Detectors and Associated Equipment 314: 212-214.
- Lecoq P (2016) Development of new scintillators for medical applications. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 809: 130-139.
- Fasoli M, Vedda A, Nikl M, Jiang C, Uberuaga B, et al. (2011) Band-gap engineering for removing shallow traps in rare-earth Lu 3 Al 5 O 12 garnet scintillators using Ga 3+ doping. Physical Review B 84: 081102.
- Yanagida T, Fujimoto Y, Koshimizu M, Kawano N, Okada G, et al. (2017) Comparative studies of optical and scintillation properties between LiGaO2 and LiAlO2 Journal of the Physical Society of Japan 86: 094201.
- Krämer K, Dorenbos P, Güdel HU, Van Eijk C (2006) Development and characterization of highly efficient new cerium doped rare earth halide scintillator materials. Journal of Materials Chemistry 16: 2773-2780.
- Wang Z, Xie Y, Cannon B D, Campbell LW, Gao F, et al. (2011) Computer simulation of electron thermalization in CsI and CsI (Tl). Journal of Applied Physics 110: 064903.
- Kozorezov A, Wigmore J, Owens A (2012) Picosecond dynamics of hot carriers and phonons and scintillator non-proportionality. Journal of Applied Physics 112: 053709.
-
Salawu Omotayo Akande*, Rabiatu Mahadi and Othmane Bouhali. Advances in Theoretical Studies of Scintillators for Positron Emission Tomography Application. Mod Concept Material Sci. 6(3): 2024. MCMS. MS.ID.000637.
-
Scintillator, Photoelectric effect, Radio pharmaceuticals, Radiation, Hygroscopic, High density, Materials, Methodology, Efficiency
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






