Effect of Structure, Color and Finish on the MIR Emission and NIR Absorption of Knitted Textiles

The influence of direct sunlight on the heat balance of single-layer dressed people is investigated within the framework of a research project. Methodically, wool, cotton and polyester yarns are knitted in series with systematically varying construction parameters. The obtained flat knitted textiles are described as fiber-based porous structures, with material characteristics like fiber or filament surfaces, or yarn and mesh pore diameter and volumes.

The transmission, reflection and absorption fractions of mid infrared radiation (MIR) and near infrared radiation (NIR) are measured with a spectrometer using small samples of the knitted textiles. The balance of low-energy MIR radiation is found slightly influenced by the textile construction. MIR radiation is absorbed in large proportions between 75 and 93% and reflected in small proportions between 6 and 14%. The balance of high-energy NIR radiation in contrast is found significantly more strongly influenced by the construction of the flat knitted fabrics, with the absorption varying between 10 and 96% and the re- flection between 4 and 67%.

A selection of the flat knitted textiles is examined as single-layer clothing with a Guarded Hotplate, whereby both the heat emission by MIR radiation and the solar heat absorption by NIR radiation are measured. The MIR heat emission varies slightly with values between 100 and 120 W m^-2. In contrast, the NIR heat absorption is far more variable with values between about 200 and 360 W m^-2 and has a significant influence on the heat balance of people. By taking NIR heat radiation balances into account, single-layer knitted clothing can be adapted more effectively to thermal conditions of heat and cold strain, which is of great practical importance in the development of functional sports, outdoor and work clothing.

Human’s thermal state is the result from the balance of body heat production and emission. Depending on body weight and degree of activity, people produce by metabolism in brain, organs and skeletal muscles usually between about 120 and 480 W heat [1,2].

Body heat emission via the skin is affected by MIR radiation and, depending on boundary conditions such as activity and climate, by other thermal processes such as convection or evaporation. If body heat production and emission correspond, the thermal state is balanced. Otherwise there is a heat or cold strain. The production and release of body heat in thermal equilibrium states can be calculated in humans with good accuracy as a function of body weight and height [3].

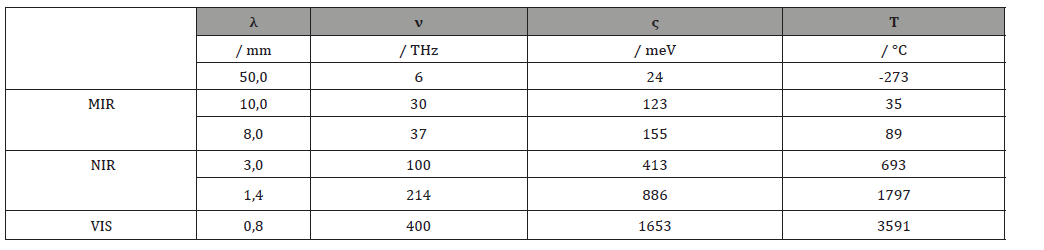
Wavelength, frequency and energy of infrared or thermal radiation (IR radiation) are a function of the temperature. The sun with a surface temperature of about 5500 °C emits high-energy shortwave near infrared radiation (NIR). In contrast, people with skin temperatures of around 30 to 40 °C emit low-energy, long-wave medium infrared radiation (MIR). By definition, the boundary between MIR and NIR is radiation of 3.0μm wave- length, 100 THz frequency and 413 meV energy emitted by bodies warm to about 700 °C (Table 1).

The radiation characteristic of undressed skin meets about 97% (light skin) to almost 100% (dark skin) an ideal black body [5]. Therefore, in the case of uncovered skin, both the absorption coefficient when absorbing solar or NIR heat and the emission coefficient when emitting body or MIR heat are approximately 100 % as symbolized in Figure 1 (left). In 1982, the World Meteorological Organization in Geneva defined a mean value of 1367 W m^-2 for the solar constant [6]. In clear weather about 1000 W m^-2 of this value arrive on the earth’s surface, in light to medium cloudiness 800 to 600 W m^-2 and in heavy cloudiness about 300 W m^-2 [7], Under the assumption that undressed people reacting like ideal black bodies, they absorb up to 1000 W m^-2 outdoors in the summer sun. Clothing modifies the NIR and MIR heat balance of humans, since the emission and absorption coefficients of clothing vary and transmission and reflection components must also be taken into account (Figure 1, right). The present research work investigates the influence of single-layer knitted clothing on the balance of NIR absorption and MIR emission.

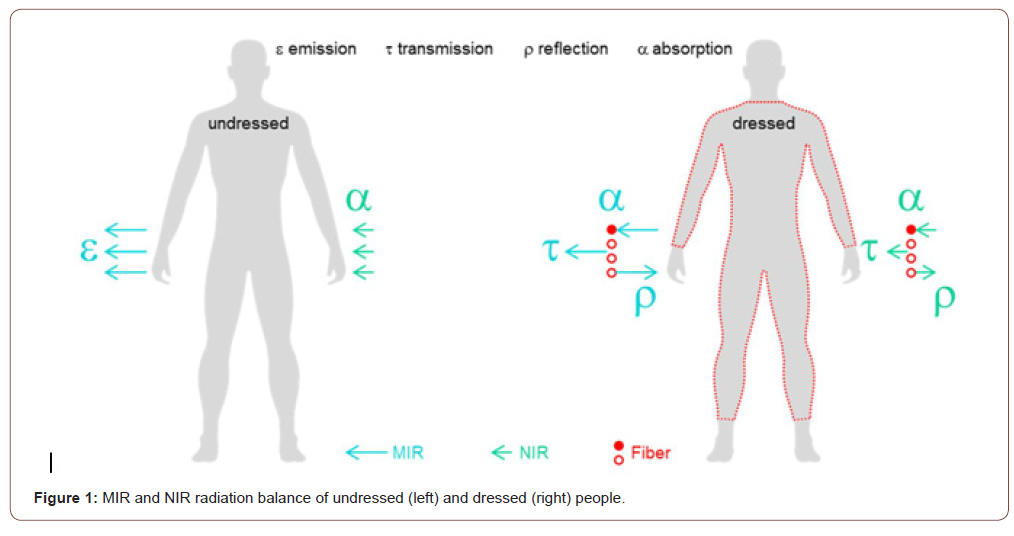
Table 1:(λ) wavelength, (ν) frequency, (ς) photon energy, (T) temperature of MIR and NIR radiation [4].

Yarns

Five raw white yarns are examined: three ring spun yarns of wool (Y1), cotton (Y2) and polyester (Y3), as well as two filament yarns of polyester with low filament number of 30 (Y4) or a high filament number of 192 (Y5).

The yarns are characterized in the laboratory. In Table 2 fiber and yarn titer are listed in dtex unit, which corresponds to 10000 m-1 in SI unit g (yarn weight per unit length). The Y1 and Y2 yarns made of wool or cotton are the heaviest with about 580 and 620 dtex respectively and have the largest diameters with 420 and 440μm respectively. The polyester ring spun yarn Y3 has about 250 dtex titer and 230 μm diameter. The polyester filament yarns Y4 and Y5 have approximately the same titer of 190 dtex, but the polyester filament yarn Y4 has low filament number of 30 and a smaller diameter of 240μm and the polyester filament yarn Y5 has high filament number of 192 and a higher diameter of 270μm.

The weights and diameters of the fibers, filaments and yarns shown in Table 2 serve as parameters for the calculation of structural dimensions, such as surface and volume of the fibers or filaments as well as equivalent diameter and volume of the yarn pores (Table 3). The calculations are carried out using the multimodal structure model (MMS) [8-12].

Table 2:Construction data of five investigated yarns from fiber or filaments (F/F).

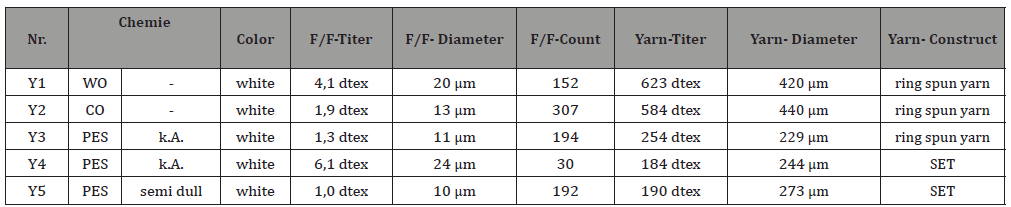
Table 3:Fiber pore structure of the yarns, (Af) fiber surface, (Vf) fiber volume, (dpy) yarn pore diameter, (Vpy) yarn pore volume, (Vy) yarn volume, (Min) minimum, (Max) maximum, (fRa) quotient of maximum and minimum.

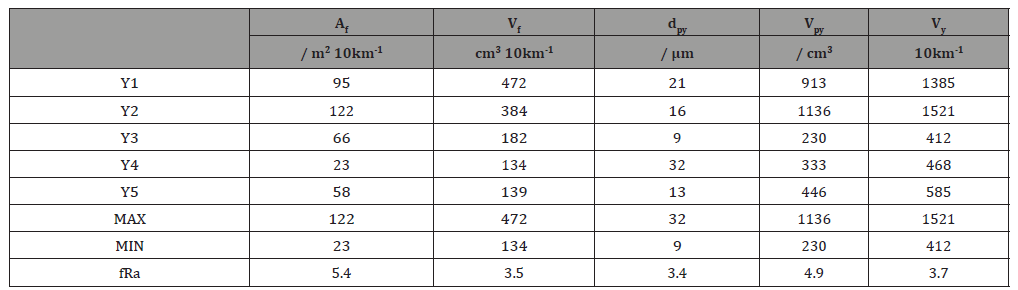
The wool and cotton yarns Y1 and Y2 not only have the comparatively largest yarn titer and diameter, fiber surfaces with about 100 and 120 m² 10 km^-1, fiber volumes with about 470 and 380 cm3 10 km-1 and yarn pore volumes with about 900 and 1100 cm3 10 km^-1 are also the largest. In the case of polyester filament yarns Y4 and Y5 with approximately the same titer of about 190 dtex, the increase filament number from 30 to 192 by a factor of 6.4 results in an increase in yarn and yarn pore volumes by about a factor of 1.3, an increase in fiber surface area by about a factor of 2.5 and a reduction in yarn pore diameter by about a factor of 2.5 (Figure 2).

In total, yarns Y1 to Y5 have a fiber or filament diameter of between 10 and 24μm. The pore diameters of 9 to 32μm are in the same magnitude of MIR radiation and mesopores [13,14].

The models are validated with microscope images of fiber and yarn cross-sections (Figure 2 top). In comparison with the modelled fiber and yarn cross-sections (Figure 2 bottom) significant similarities can be seen. In case of the filament yarns Y4 and Y5, the diameters are considerably larger in mechanical free condition of the spooled yarn than in the tensioned condition of the knitted yarn. This is not the case for ring spun yarns Y1, Y2 and Y3

Filament yarn Y5 is used to produce dyed variants: bath-dyed yarns Y6 (grey) and Y7 (black) as well as spun-dyed yarns Y8 (grey) and Y9 (black). In terms of construction (Table 2) and structure (Table 3), the dyed yarns Y6 to Y9 largely correspond to the raw white starting yarn Y5.

Knitted textiles

The knitted textiles T1 to T26 are designed from yarns Y1 to Y9, right-right (RR) on a flat knitting machine (Stoll, type CMS 33JC, gauge E12, width 1270mm, needle count 1198). An exception is the T6 knitted fabric designed for right-left (RL) knitting on a single jersey or circular knitting machine (Mayer & Cie, type MV4-3.2, gauge E24, 16-inch diameter (406mm), needle count 1200). RR textiles are knitted with two needle bars, which therefore have right stitches on both knitted surfaces. RL textiles are knitted with only one needle bar, which therefore have right stitches on one knitted surface and left stitches on the other knitted surface.

The 26 knitted fabrics vary in weight between approximately 220 and 540 g m^-2, thickness between 0,5 and 2,5 mm, yarn length between approximately 5 and 12 km m^-2 and stitch number between approximately 70 and 400 cm^-2 (Table 4).

Table 4:Dimensions of the knitted construction, the individual values of 26 examined knitted textiles are summarized to (min) minimum, (max) maximum and (fRa) quotient of maximum and minimum, the individual values are listed in [15].

The knitted fabric data in Table 4 together with the yarn data in Table 2 are used to calculate metrics of the knitted textile structure. In addition to the surface and volume of fibers or filaments and equivalent diameters and volume of yarn pores, this also includes the equivalent diameter and volume of mesh pores. The knitted fabrics are combined into measurement series for subsequent analyses.

The knitted fabrics T1 to T5 (Figure 3) do not differ systematically, since parameters of polymer chemistry (WO, CO, PES) and yarn structure (fiber, filament) vary equally. Exceptions are the knitted fabrics T4 and T5, which exclusively differ in the filament number of the yarns. The increase in the number of filaments from 90 to 576 by a factor of about 6.5 results in an increase in the filament surface area and yarn pore volume by a factor of about 2.5 and 1.5, respectively, and in a reduction in the mesh pore diameter and volume by a factor of about 2.0 and 3.5, respectively.

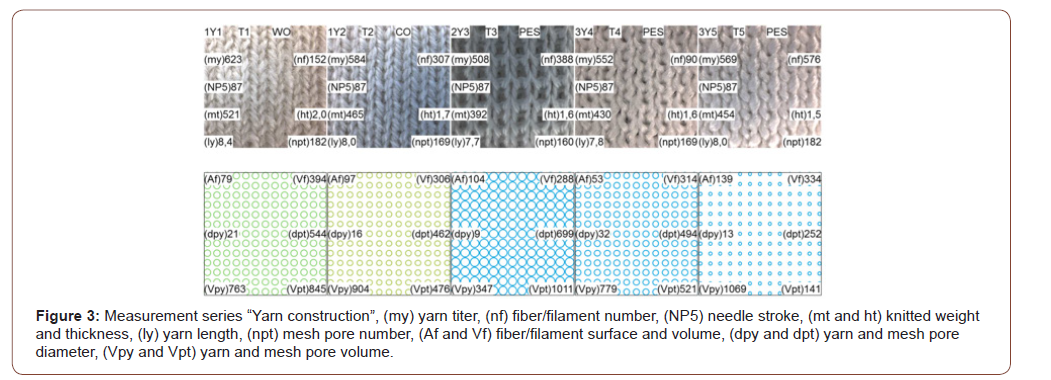
The yarn Y4 is circular knitted on an E24 single jersey machine in RL. The corresponding knitted fabric T6 is lightest at 223 g m^-2 and thinnest at 0.6mm. Filament surface with 27 m² m^-2, filament volume with 163 cm3 m^-2 and mesh pore volume with 80 cm3 m^-2 are additionally lowest. The mesh pore number is the highest at 400 cm^-2 and the mesh pore diameter the smallest at 198 μm. For flat knitted textiles T7, T8 and T9, the increase of yarn number by 2, 3 and 4 results in approximately doubling the number of filaments, fabric weight, filament surface and filament volume and yarn pore volume. In contrast, mesh pore diameter and volume are reduced by a factor of about 1.5 (Figure 4).

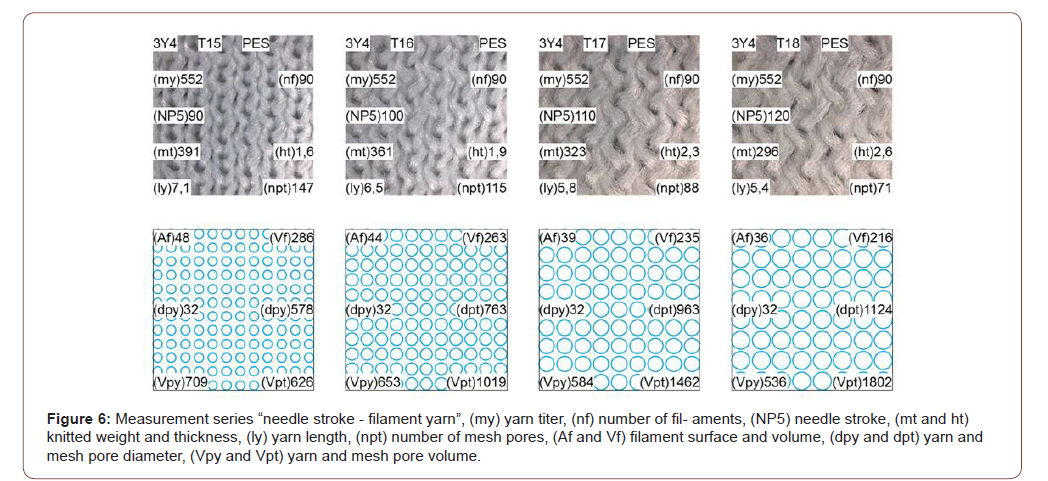
On the flat knitting machine used, the dimensionless NP5 parameter is used to configure the needle stroke. The mesh diameters increase with the NP5 scalar. For the knitted textiles T10 to T14 made from the double knitted polyester fiber yarn Y3, the increase of the NP5 from 7.8 to 9.0 by a factor of about 1.2 results in an increase of the mesh pore diameter and volume by a factor of up to about 1.5 and a reduction of the fiber surface area and volume by a factor of up to about 1.5 (Figure 5). For knitted fabrics T15 to T18 made from the triple knitted polyester filament yarn Y4, the increase in NP5 from 8.7 to 12.0 by about a factor of 1.5 results on one hand in an increase in thickness, mesh pore diameter and volume by a factor of up to 3.5, and on the other hand in a reduction in filament surface area and volume by a factor of up to 2.5 (Figure 6).

The filament yarns Y5 to Y9 are structurally similar. Therefore, the knitted fabrics T5 (Figure 3) and T19 to T22, that are constructed from them, are structurally similar as well. In contrast different are dyeing process and color of the yarns or textiles respectively. Yarn Y5 or knitted textile T5 are raw white, yarn Y6 or knitted fabric T19 are bath-dyed grey (bg), yarn Y7 or knitted fabric T20 are bath-dyed black (bb), yarn Y8 or knitted fabric T21 are spun-dyed grey (sg) and yarn Y9 or knitted fabric T22 are spun-dyed black (sb) (Figure 7).

In terms of knitting technology, the flat knitted fabrics T23 to T26 (Figure 8) are identical to T4 (Figure 3). While T4 is untreated, T23 to T26 have been treated with different IR- active substances (Figure 8). The knitted fabric T23 treated with EnergearTM (En) and the knitted fabric T24 treated with Solar^+TM (So+) retain their white color. In contrast, knitted fabrics T25 and T26 were dyed black, knitted fabric T25 with IR-active Coldblack® technology (+CB) and knitted fabric T26 without (-CB).

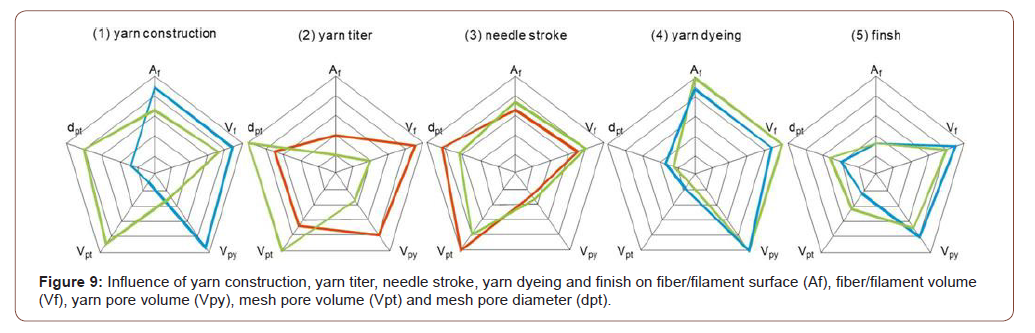
In summary, the varied parameters in the knitting process influence the fiber-pore structure of the flat knitted fabrics as shown in Figure 9:

• Compared to a ring spun yarn (Figure 9-1, green line), the use of a filament yarn (Figure 9-1, blue line) increases the yarn pore volume by up to about 60 % and reduces the mesh pore diameter and volume by up to about 60 %. In contrast, the change in filament surface and volume is relatively small (compare Figure 3).

• By increasing yarn titer (Figure 9-2, red line), filament surface, filament volume and yarn pore volume in the flat knitted textile are increased by about 20 to 50 % and the mesh pore diameter and volume are reduced by up to about 30 % (compare Figure 4).

• By increasing needle stroke (Figure 9-3 red line), the filament surface, filament volume and yarn pore volume of the knitted textile are reduced by up to about 10 % and the mesh pore diameter and volume are increased by about 20 to 25 % (compare Figure 5 and Figure 6).

• The measuring series “yarn dyeing” is made of polyester filament yarns with a filament number in yarn cross-section of 192. The structural differences within the measurement series are slight, as shown in Figure 9-4 using the knitted textiles T20 (green line) and T21 (blue line) (compare Figure 7).

• The “Finish” measurement series is made from polyester filament yarns with a filament number in the yarn cross section of 30. Within the measurement series, the differences in the filament pore structure are slight, as shown in Figure 9-5 using the knitted textile T4 (green) and T25 (blue) (compare Figure 8).

• The differences in the filament pore structure between the “yarn dyeing” and “finish” measurement series are considerable. By increasing the filament number of the yarns, the filament surface and yarn pore volume in the flat knitted fabric are in- creased by about 30 to 50 % and the mesh pore diameter and volume are reduced by about 25 to 35 %. In contrast, the filament volume remains largely unaffected by the number of filaments in the yarn cross-section (compare Figure 9-4 and Figure 9-5).

Measurement of MIR and NIR radiation

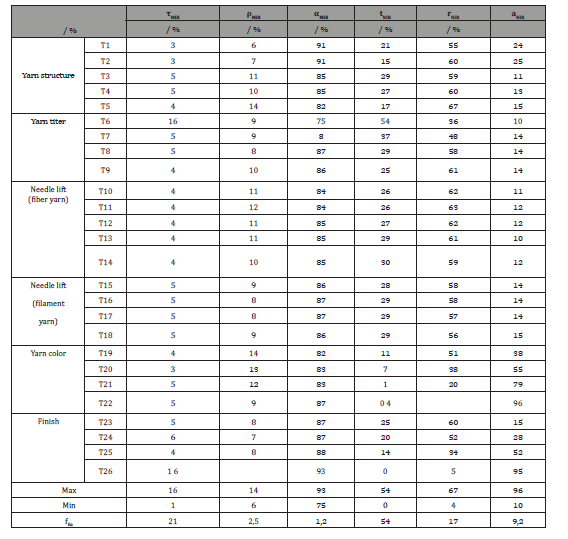
The MIR and NIR radiation are determined experimentally with a modified FT-IR vacuum spectrometer Vertex 80 from Bruker, which is equipped with PTFE integration sphere, silicon carbide rod as MIR radiation source (body heat) and tungsten radiator as NIR radiation source (solar heat). In measurement series separated according to MIR and NIR radiation, the transmission and reflection fractions are measured on small 8 x 4 cm² specimens. The absorption shares are calculated according to the balance equation τ + ρ +α = 1. Table 5 shows the results for 26 flat knitted textiles.

The raw white flat knitted fabric T5 with 139 m² m^-2 filament surfaces and 252μm macro pore diameter (compare Figure 3) has the highest MIR reflection with 14 % and the highest NIR reflection with 67%. The raw white flat knitted textile T4 with 53 m² m^-2 filament surface and 494μm macro pore diameter (compare Figure 3) has a lower MIR reflection of 10% and a lower NIR reflection of 60%.

The black flat knitted fabric T26 with 58 m² m^-2 filament surface and 398μm macro pore diameter (compare Figure 8) has the lowest MIR reflection (6%) and the highest MIR absorption (93%). The black flat knitted fabric T22 with 142 m² m^-2 filament surface and 274μm macro pore diameter (compare Figure 7) has a slightly higher MIR reflection of 9% and a slightly lower MIR absorption of 87%. In the NIR radiation balance, the knitted textiles T22 and T26 are mostly alike and have the lowest NIR reflection with 4 % and 5% and the highest NIR absorption with 95 % and 96 %. In addition, the knitted textiles T22 and T26 have the lowest NIR transmission with 0 % each.

The highest MIR transmission (16%) and the highest NIR transmission (54%) is achieved with the raw-white circular knitted fabric T6, which is smallest in filament surface (27 m² m^-2), fiber volume (163 cm3 m^-2) and macro pore diameter (198μm), and highest in number of macropores (400 m-1) (compare Figure 4).

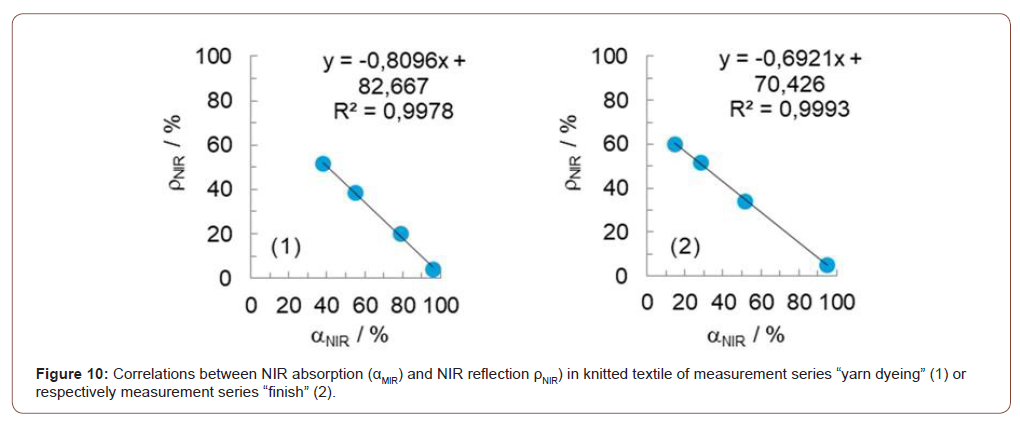
The transmission in the MIR and even more in the NIR can obviously be controlled to a certain extent via the knitted structure. With the same structure, the absorption and reflection fractions are determined inversely by the fiber or filament surfaces or their color (Figure10(1)) or finish (Figure10(2)).

This is particularly significant in the case of high-energy NIR radiation balances, where NIR absorption varies between 10 and 96%, NIR reflection between 4 and 67% and NIR transmission between 1 and 54% much more strongly than in the case of lowenergy MIR radiation balances, which are dominated by MIR absorption between 75 and 93%. The MIR reflection of the knitted fabrics varies between 6 and 14% and the MIR transmission

Measurement of MIR and NIR heat

Corresponding heat measurements are performed with a Guarded Hotplate Measuring Method (GHP) [16-21]. The square aluminum measuring plate has 25cm edge length, 625cm² area, 100μm thickness and 90.000 pores with 400μm diameter.

The pore number of the measuring plate corresponds with 144 cm^-2 to the average sweat pore number of human skins.

To prevent lateral heat losses, the measuring plate is surrounded by an equitherm heated frame (Thermal Guard). Five temperature sensors for electronic temperature regulation are located on the underside of the measuring surface. The measurements are made at 22.1 ± 0.1 °C ambient temperature, 53 ± 1 % relative humidity and 0.06 ± 0.01 m s-1 air velocity. The measuring plate of the GHP is electrically heated to temperatures between 30 and 40 °C, the human skin temperatures corresponding to different vasomotor states [21].

The measurements are carried out on four flat knitted fabrics with decreasing MIR reflection of 14% (T5), 10% (T4), 9% (T6) and 6% (T22) or respectively decreasing NIR reflection of 67% (T5), 60% (T4), 36 % (T6), 5 % (T22) (Table 5). For the measurements, the knitted textiles cover the measuring plate like clothing on the skin.

Table 5:MIR radiation balance (αMIR, ρMIR, τMIR) and NIR radiation balance (aNIR, rNIR, tNIR) of transmission, reflection and absorption, (min) minimum, (max) maximum, (fRa) quotient of maximum and minimum.

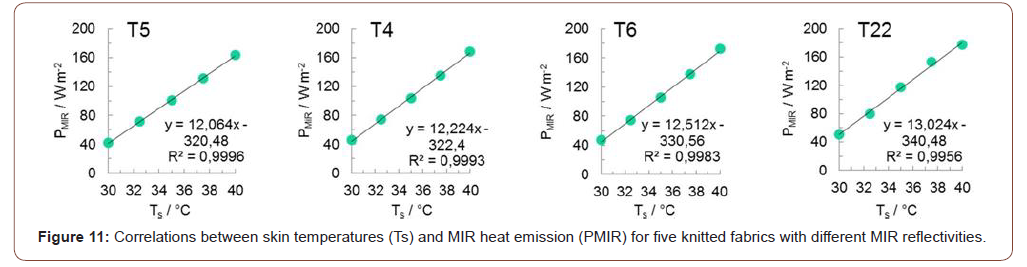
The resulting MIR heat emission of the Guarded Hotplate is determined in the unit W m^-2. The MIR heat emission increases proportionally to the skin temperature. In the case of the investigated knitted textiles, the MIR heat emission is about 30 to 50 W m^-2 at 30 °C skin temperature and about 160 to 180 W m^-2 at 40 °C skin temperature (Figure 11).

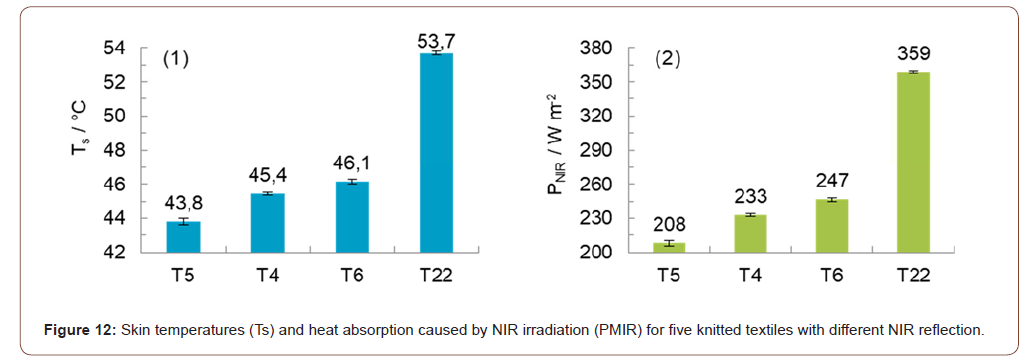
To measure NIR heat absorption, the textile covered measuring plate isn´t electrically heated but irradiated with an NIR emitter (Osram IR1 Therotherm, 240 V, 250 W) placed 40cm above the center. The temperature of the measuring plate as a result of NIR irradiation is determined at equilibrium and increases to 43,8 °C (T5), 45,4 °C (T4), 46,1 °C (T6) and 53,7 °C (T22) (Figure 12(1)) with decreasing NIR reflection of the respective knitted textile. Using the equations of the correlation lines in Figure 11 the power corresponding to the NIR irradiation can be calculated and be interpreted as NIR heat absorption of the single-layer dressed human body, which increases with decreasing NIR reflection to 208 W m^-2 (T5), 233 W m^-2 (T4), 247 W m^-2 (T6) and 359 W m^-2 (T22) (Figure 12(2)).

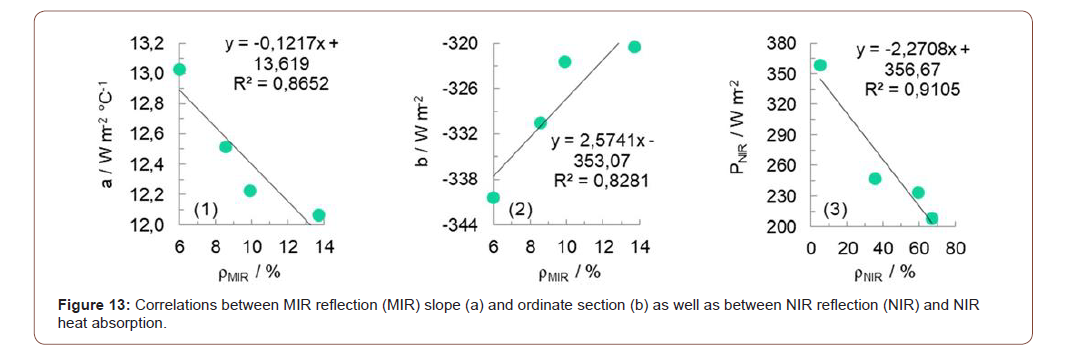
In the case of the knitted textiles T5, T4, T6 and T22, the correlations between skin temperature and MIR heat emission show significant correlations in Figure 11: The slope of the correlation lines decreases with increasing MIR reflection (Figure 13(1)) and the ordinate section increases linearly (Figure 13). In addition, NIR heat absorption decreases linearly with increasing NIR reflection (Figure 13(3)).

Using the equations in Figure 13(1) and Figure 13(2) the MIR heat emission can be calculated for the investigated knitted textiles and using the equation in Figure 13(3) the NIR heat adsorption can be calculated. The results presented in Table 6 can be summarized as follows:

Table 6:MIR heat emission (P_MIR), and NIR heat adsorption (P_NIR) and difference of both (NIR_MIR), (min) minimum, (max) maximum, (fRa) quotient of maximum and minimum.

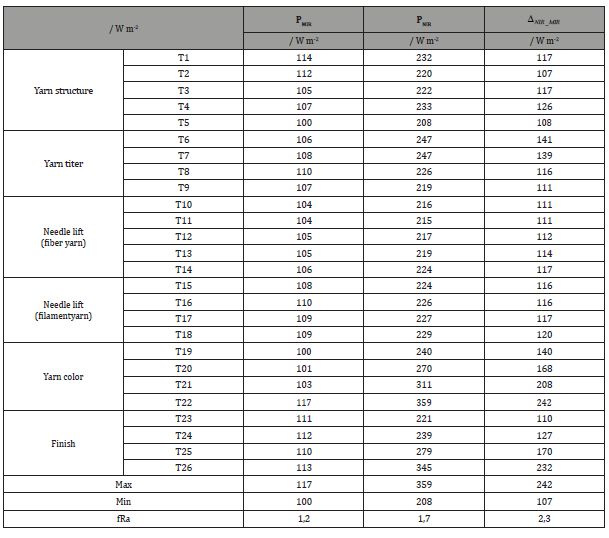
For knitted textile T4, the number of filaments and thus the filament surface is reduced by about 90 m² m^-2 compared to knitted fabric T5 (Figure 3). As a result, NIR reflection reduces by 7% and NIR heat absorption increases by 25 W m^-2.

For knitted textiles T9, T8 and T7 (Figure 4) the yarn titer is systematically reduced and consequently the filament surface by about 30 m² m^-2 and the filament volume by about 200 cm³ m^-2. In addition, the mesh pore diameter increases by about 200μm and the mesh pore volume by about 350 cm³ m^-2. As a result, NIR reflection is reduced by 13 % and NIR heat absorption is increased by about 25 W m^-2, respectively.

In measurement series of Figure 5 and Figure 6 the needle stroke and consequently the mesh length increase from left to right. As a structural result, filament or fiber surfaces decrease by about 10 m² m^-2 and mesh pore diameters increase by up to about 600μm and the mesh pore volume increases by up to about 1000 cm³ m^-2. In consequence the NIR reflection reduces by up to about 3 % and NIR heat absorption increases by up to about 10 W m^-2.

The color variations of the measurement series in Figure 7 result in a reduction of NIR reflection by up to about 55 % and an increase of NIR heat absorption by up to about 130 W m^-2 compared to the raw-white reference knitted textile T5 (Figure 3).

Regarding the measurement series in Figure 8 the EnergearTM finish of knitted textile T23 shows no significant influence on NIR reflection or NIR heat absorption compared to the untreated reference knitted textile T4 (Figure 3). The Solar^+TM technology is designed to increase warming up of white clothing in sunshine. In case of knitted textile T24 the Solar^+TM technology reduces NIR reflection by 15% compared to the untreated reference knitted fabric T4 (Figure 3) and increases NIR heat absorption by about 10 W m-2. The Coldblack® technology is designed to reduce the warming up of black clothing in sun- shine. In fact, the black knitted textile T25 with Coldblack® technology increases NIR reflection by about 30% and reduces NIR heat absorption by about 65 W m-2 in comparison to the black reference knitted textile T26 without Coldblack® technology.

It is a philosophical question whether 5 yarns or 26 knitted fabrics were examined in this study. It can be argued that 5 yarns were examined and knitted for this purpose to 26 structures, and it can as well be argued that 26 knitted fabrics were examined, varying fiber, yarn, knitting, dyeing and finishing parameters.

From engineering or technical point of view, knitted fabrics consist of yarns and stitches, and from thermodynamic point of view they consist of fibers and pores. In yarns, the fibers are on average about 10 and 30μm apart and creating mesopores. Between yarns in the meshes, the fibers are about 200 to 1100μm apart and creating macropores. Knitted fabrics have therefore a characteristic bimodal pore size distribution.

Apart from weight per unit area, thickness and stitch number, knitted fabrics are described by nominally scaled parameters, such as the weave, which are not uniformly defined, and which are very difficult to translate into other languages. According to the results of this study, knitted fabrics can be characterized by structural parameters of general porous material, which have the same meaning in every language, such as fiber surface, pore diameter and pore volume. In order to establish and test this model concept, the knitted fabrics are presented in detail in chapter 3.2. It is described that structure parameter systematically change with yarn construction (Figure 3), yarn titer (Figure 4) or needle stroke (Figure 5 and Figure 6) and stay approximate constant with yarn dyeing (Figure 7) or finish (Figure 8). Correlations between structural parameters applicable exclusively to textiles and structural parameters applicable to all porous materials must be investigated in future studies.

As far as we know, a Guarded Hotplate was first time used in this study to measure NIR heat absorption of dressed skin. Based on the solar constant it can be estimated that undressed people in direct sun light absorb up to 1000 W m-2 heat. In the NIR heat absorption measurements of this study the NIR emitter was placed 40 cm above the meas- uring plate of the Guarded Hotplate and resulted NIR heat absorption of about 360 W m-2. Depending on the vasomotor condition, the MIR heat emission varied at the same time between about 60 W m^-2 (at 30 °C skin temperature) and 190 W m^-2 (at 40 °C skin temperature). Assuming average skin temperatures of 35 °C, the MIR heat emission is about 120 W m^-2. Abstracted to humans this means that undressed skin absorbs about 240 W m-2 more heat in form of NIR radiation than they emit heat inform of MIR radiation when exposed to direct sunlight.

Compared to undressed skin the heat balance only changes little for single-layer clothing that absorbs MIR or NIR radiation by more than about 95% or reflects it by less than about 5%, as is the case for example with black knitted like T22 or T26. However, in single-layer clothing that reflects MIR radiation by more than about 10 % or reflects NIR radiation by more than about 65 %, as is the case with the knitted textiles T2 or T5, the solar heat absorption is reduced to less than 220 W m^-2 and the heat balance between solar heat absorption and body heat emission is reduced to less than 110 W m^-2.

Although the 26 flat knitted fabrics examined differ significantly in terms of fiber raw material, yarn, knitting parameters, color or finish, their MIR reflection varies by only less than 10 % and the MIR heat emission of the single-layer dressed Guarded Hotplate varies by only about 20 W m^-2. These values are relatively low, considering that working people produce 120 to 480 W by metabolism. In contrast, the NIR reflection of the knitted textiles investigated varies by more than 60%. Therefore, the solar heat absorption of the single- layer Guarded Hotplate varies by up to about 25 W m^-2 depending on the fiber and pore structure, by up to about 65 W m^-2 depending on the IR-active finish and even by up to about 130 W m^-2 depending on the color, and thus has a significant influence on the heat balance of people.

In the measurements performed, the MIR heat emission of the Guarded Hotplate is approximately inversely proportional to the MIR reflection of the knitted textiles and the NIR heat absorption is approximately inversely proportional to the NIR reflection of the knitted textiles. In summary, the investigations show that single- layer knitted clothing effects hu- mans’ temperature regulation stronger by NIR heat absorption than on MIR heat release. Within the framework of further research projects, it will be investigated how single-layer knitted clothing thermally function via the mechanisms of conduction, convection or evaporation or how multi-layer clothing affects the MIR-NIR heat balance of humans.

Usual experimental limitations apply to the measurements performed . In the spectrometer and Guarded Hotplate measurements, the MIR radiation sources do not exactly correspond to human body heat and the NIR radiation sources do not exactly correspond to solar heat. This limits the abstraction to real situations as well as the fact that people are irradiated by the sun at very different angles. In this context, Guarded Hotplate measurements with systematically variable NIR radiator distance will be performed in future.

The measurements of the MIR and NIR radiation balances with the spectrometer were performed on 26 knitted fabrics and statistics are correspondingly meaningful. In contrast, the more complex measurements of the MIR and NIR heat balances with the Guarded Hotplate were carried out on only four knitted fabrics, because the effort of the measurements was high, and the variation of many samples in MIR and NIR radiation balances were small. Further measurements will be necessary in the future to increase accuracy and validity of the derived models. An improved Guarded Hotplate is currently built up for this purpose.

Guarded Hotplate methods can not only used for measurements of human heat emission via MIR, convection and evaporation but also for measurement of NIR heat absorption which is of great practical interest in the development of functional clothing because NIR heat absorption has in many situations great influence on human temperature balance and thermal comfort. By taking NIR heat absorption into account, single-layer knitted clothing can be adapted more effectively to different heat and cold strain conditions. The presented measuring methods will be extended and refined in the future.

The IGF research project AIF18791N and IGF 19472 BR was funded by the Federal Ministry of Economics and Energy on the basis of a decision by the German Bundestag. Thank you very much.

Authors declare no conflict of interest.

1. Pandolf KB, Givoni B, Goldman RF (1977) Predicting energy expenditure with loads while standing or walking very slowly. J Appl Physiol Respir Environ Exerc Physiol 43(4): 577-581.
2. (1993) Standard DIN EN 27243:1993: Determination of the heat load of the worker using the WBGT index (wet bulb globe temperature).
3. Wendt E, Bauer B, Wölfling B, Gresser GT, Krzywinski S, Claßen E (2019) Method development for modelling, design and digital representation of outdoor and protective clothing based on geometric, mechanical and thermal parameters, final report on the research project IGF 19472 BR.
4. (2007) ISO 20473, Optics and photonics - spectral bands.
5. Hardy JD, Muschenheim C (1934) The radiation of heat from the human body. iv. the emission, reflection, and transmission of infra-red radiation by the human skin. Journal of clinical investigation 13: 817.
6. Wagemann HG, Eschrich H (1994) Grundlagen der photovoltaischen Energiewandlung, Teubner, Stuttgart.
7. Solar constant.
8. Schleicher N (2013) Surface and pore structures in knitted fabrics with conductive fibres, bachelor thesis.
9. Basaran T (2013) Influence of knitting technology on the pore structure of knitted fabrics, bachelor thesis.
10. Köly A (2016) Development of pore structure and pore volume models for knitted fabrics, master thesis p.62.
11. Luley D (2016) Development of gradually varying structures in knitted fabrics, research report . p. 102.
12. Mark A, Psikuta A, Bauer B, Rossi RM, Gresser GT (2018) Artificial skin for sweating guarded hotplates and manikins based on weft knitted fabrics. Textile Research Journal 49(4): 657-672.
13. Hartge KH, Horn R (1999) Introduction to soil physics. p.372.
14. Rowell DL (1997) Bodenkunde - Untersuchungsmethoden und ihre Anwendung. Springer, Berlin, Heidelberg, Germany.
15. Bauer B, Gresser GT (2018) Development of basic knowledge for the selective use of heat radiation in knitted fabrics for functional clothing, final report on the research project IGF 18791 N.
16. Lörcher C (2013) Design of a Guarded Hotplate for measurement of dry and evaporative heat emission, master thesis.
17. Bauer B, Koch S, Mark A (2014) Guarded-Hotplate-Measurements for heat transfer balancing, Ambience’14&10i3M, Tampere, Finland
18. Krutzsch T (2017) Heat Radiation Selective Knitted Fabrics. Master Thesis, p.76.
19. Saur A (2016) Analysis and optimization of the Guarded Hotplate 2 for the simulation of human vasomotor functions, bachelor thesis in German language, University Stuttgart, Germany, p.77.
20. Mark A (2016) Development of a measurement device investigating properties on clothing textiles - Innovative construction of a dynamic measurement instrument for investigating thermodynamic properties on textiles and clothing textiles.
21. (2002) ASTMD1518, Standard Test Method for Thermal Resistance of Batting Systems Using a Hot Plate, Conshocken: American Society for Testing Materials.