Elementary Physics of Magnetic Field (monopolies)

Any axiomatic theory is built on a strictly defined Orthogonal Frame. This applies to both Particular Theories and Physics as a whole. On the basis of a verified orthogonal frame, ELEMENTS are built, from which a Unified Consistent Description of Nature can be composed. But, unfortunately, in Physics, which has the ability to experimentally verify the selected Frames, many PROVISIONS are used that are defined very loosely. So the Magnetic Field was discovered long ago. And it has long been actively used, from the first magnetic compass needles to electromagnets, electric motors and data recording. But as it was discovered as a mystical geomagnetic phenomenon, so, without any physical justification, simply mathematically fixing it in the form of a rotor, this mysticism in the theoretical description of Magnetism was abandoned. Hence the ongoing attempts to search for/discover a magnetic charge, again a mystical magneton. Hence the mysticism of the most advanced theoretical calculations and conclusions, since the errors of the «scientific definitions» of the Magnetic Field are prolonged in Electrodynamics and the Theory of Relativity. Hence the fact that, after completing the work on Quantization [1], my short work on a strict DEFINITION of the Magnetic Field, the Idea of which arose after the discovery of the incorrect interpretation of the EXCLUSION of the speed of light [2], resulted in a whole cycle of works [3-6], in which an analysis was made of various aspects of the Magnetic Field, which until now had no strict scientific explanation and were used in a very contradictory way. In fact, we still did not even have a strict Definition of the Magnetic Field, but only had a bad infinity in attempts to hide the MISUNDERSTANDING of ELEMENTARY THINGS behind a more «sublime» - «quantum» MISUNDERSTANDING.

The critical analysis conducted in the cycle of previous articles showed that modern Quantum Mechanics, which has departed from the QUANTIZATION Principles laid down by Planck and expanded by Einstein, has become like a colorful Chinese screen with dragons for both Science itself and the Public Consciousness. Only instead of the painted fantastic dragons, shadows of imaginary Schrödinger solutions are exhibited on it. Complex solutions of the Schrödinger equation contain ELEMENTARY Mathematical errors due to the violation of ELEMENTARY Logic - imaginary terms of the solutions of the real Schrödinger equation were invented with a physical meaning (Copenhagen interpretation), and physically justified imaginary terms of the equation itself were missed.Previously, Richard Feynman came closest to UNDERSTANDING this problem of Quantum Mechanics, saying: «My path integrals, like the Schrödinger equation, do not explain Quantum Mechanics. But my equations provide a simpler way to solve this Schrödinger equation.» But Feynman did not dare to openly doubt the correctness of the Schrödinger equation itself. Just as Schwinger did not dare in his works on fields, sources and sinks [7, 8]. And it was precisely the analysis of the Magnetic Field that helped me finally become convinced that the Fundamental Problem exists, the very definition of which is still based on artistic images of «Descartes’ gimlets», also hidden behind a mathematical screen - behind the rotor.

So, after finishing the combing (roughly) of Quantum Mechanics, I did not immediately, as planned, proceed to combing Einstein’s Theory of Relativity. It turned out that Einstein conceptually constructed it, after Bohr’s attack on him and Planck, like Schrödinger, also using Imaginary. But the Imaginary used by Einstein were already embedded in Maxwell’s equations themselves, and also without sufficient physical justification - Maxwell simply formally used Heaviside’s mathematical physics, without attaching any importance to his interpretation of Heaviside’s «telegraph equations». And, thus, the lack of rigor in the Definition of the Magnetic Field resulted in the Problem of the Speed of Light and the entire construction of Einstein’s Theory of Relativity. In view of the revealed Fundamentality of the correct UNDERSTANDING and the correctness of the DESCRIPTION of the Magnetic Field, without its strict REDEFINITION, both Quantum Mechanics itself and the Theory of Relativity cannot be strictly mathematically and physically described and are still built on the sand of fantasy.

According to Albert Einstein’s wise statement: «Some equations of Classical Physics allow rewriting in operator form», it is the CORRECT Classical Concepts and Models that are the Basis of any physical, including Quantum Theories. And in modern Physics, the MISUNDERSTANDING OF THE BASICS is often hidden behind «Definitions», which are, to put it mildly, not strict, and it would be more correct to say, are not Definitions at all. Thus, the description of Magnetism given in primers, simply embellished with formulas, was driven into Descartes’ Concepts about «gimlets», without even conducting the necessary analysis of either the Ampere Force or the Lorentz Force.

Here are several examples of similar “Definitions” of the Magnetic Field, now used in Physics textbooks.

The Magnetic Field is “defined” in a SPECIAL way through the Magnetic Moment!

“The Magnetic Field can be called a SPECIAL type of matter through which interaction occurs between moving bodies or bodies with a magnetic moment.”

And it is complemented by “Determination” through Magnetic Induction!

“The main quantitative characteristic of the Magnetic Field is the vector of Magnetic Induction B (vector of Magnetic Field Induction).”

At the same time, Magnetic Induction itself is OVERDETERMINED through the Magnetic Field!

“Magnetic Induction is a vector physical QUANTITY that is FORCE! Characteristics of the Magnetic Field, namely the Characteristics of ITS Action on moving charged particles and on bodies possessing a Magnetic Field.”

Likewise, the MISUNDERSTANDING of Magnetism hides behind the Lorentz Force!

Magnetic Induction is such a vector that the Lorentz Force acting from the Magnetic Field on a charge moving with speed is equal to

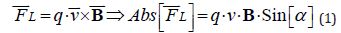
And it is added (for greater importance, but they hit the mark!): “Magnetic Induction IS the main Fundamental Characteristic of the Magnetic Field, similar to the vector of Electric Field Tension” (Figure 1a).

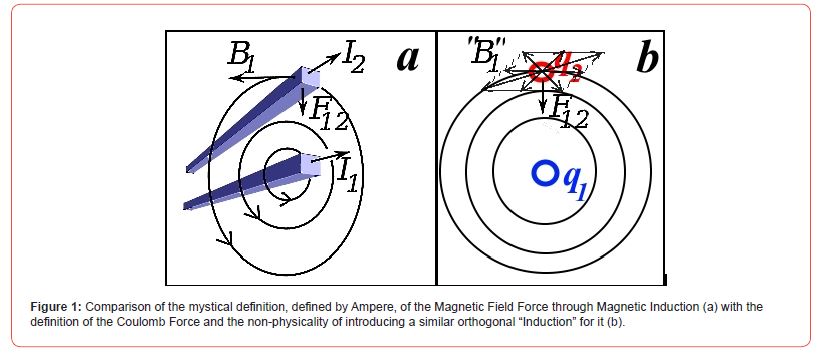
It is necessary to immediately note the senseless stretch in the comparison/comparison of Magnetic Induction and Electric Induction. Electric Induction is initially introduced completely differently. It is an Electric Field arising (and measured under certain conditions) in a material, induced by an external Electric Field. Whereas the formal equating of the Magnetic Field to Magnetic Induction B in a vacuum does not correspond in any way to the direction of the Ampere Force (Figure 1a). The Ampere Force, as can be seen from (Figure 1), is initially orthogonal to the external Electric Field along the velocity (current). The Magnetic Force is COLLINEAR to the Coulomb Force between charges, perpendicular to the current line! And the true additional Orthogonal Characteristic of the Magnetic Field, as will be shown below, arises as a consequence of the Ampere Force, as its derivative component.

So, in the traditional “Definitions” of the Magnetic Field, behind the scientism, there is an obvious MISUNDERSTANDING of the Magnetic Field, which is only strengthened by the “virtual” photons that supposedly generate it. The absence of “Descartes’ gimlets” in electrostatics saved Coulomb’s Law from “virtual” photons in the DEFINITIONS of the Electric Field. And it will not work to attach “orthogonal gimlets” to the spherical equipotential at the point where the test charge is located. Unlike the symmetry of the “rotation” of the cylindrical magnetic equipotentials (imaginary) (Figure 1a), introduced like the Magnetic, “Induction” of the Coulomb Field would rotate all spherical equipotentials at once in all directions at all points of the sphere and (Figure 1b). Similar to the illogical “DEFINITIONS” given above, in many textbooks on electromagnetism, the full force itself - the Lorentz force is used as a definition of the electric and magnetic fields E and B (as its component-parameters).

In this case, the Lorentz force (and not as it should be logically - the Ampere force) is presented as a simple empirical relationship:

“The electromagnetic force F acting on a test charge at a given point and time is a certain function of its charge q and velocity v, which can be parameterized by exactly two vectors E and B in functional form (it would be better to say this - uniquely parameterized by two vectors). “

And this “definition” of the Magnetic Field as part of the general electromagnetic interaction also suffers from juggling (hypocrisy, only formulas are used instead of opaque thimble cups), because The General Interaction itself is introduced using the Magnetic Field as an independent orthogonal characteristic.

The mysticism of all the listed definitions of the Magnetic Field is due to the fact that the initially experimentally measured Ampere Force and its logical continuation the Lorentz Force are (re)-“determined” through an indefinite (implied) NON-INVARIANT relative to the Lorentz transformation quantity Magnetic Induction B, which, in essence, not determined:

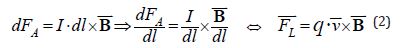
Whereas the standardly introduced Electric Induction is a CONSEQUENCE of the change of the external Electric Field applied by the medium to the sample (or to the selected volume of space). At the same time, it is already evident from the ELEMENTARY figure 1a that in all the listed «Definitions» of the Magnetic Field, the Confusion of Magnetic Force with Magnetic «Induction» entered, which is also orthogonal to the Ampere Force. And such an introduction of «Induction» for the spherical Electric Field of Coulomb, as already noted (Figure 1b), would give its complete uncertainty in angle.

And this confusion in almost all «DEFINITIONS» of the Magnetic Field, explicitly or implicitly, is connected with the fact that Magnetic Charges were initially used, by analogy with the Electric Field. Even Coulomb himself, in the first attempt to redefine «Descartes’ gimlets», constructed the Magnetic Law of Coulomb with fluids, completely analogous to the Electrostatic and Gravitational Laws. But the experimental discovery of Ampere showed that the dependence of the Magnetic Force on the distance from the conductor with current has a character that does not correspond to the Coulomb Law. And Ampere’s discovery is of fundamental importance, because it showed the connection of the Magnetic Field with the Electric Field. But this CONNECTION discovered by Ampere, in fact a relativistic effect, was not analyzed strictly enough and understood to the end.

The currently used, in fact, sophistical «Definitions» of the Magnetic Field only hide the misunderstanding of its ESSENCE and properties and lead to a pile of formulas that do not describe many Magnetic Effects even in the first approximation - requiring numerous corrections. Therefore, it is not surprising that in practice in Magnetism I use empirical classical formulas. Whereas without a correct classical Description of Magnetism at the macroscopic level, according to the above-mentioned «formula» of Einstein, there can be no talk of constructing a Quantum Theory of Magnetism. Whereas theorists, under a far-fetched (masking the MISUNDERSTANDING of the Classics) pretext about the Quantum Nature of Magnetism, shifted the classical Description of Magnetism onto the shoulders of art historians. Thus, with their theories they buried the UNDERSTANDING of Magnetism even deeper. With the same success, under the pretext of the Quantum Nature of Coulomb’s law, one could entrust art historians and Electrostatics or continue to build «Physics» on Schrödinger’s «sand», reducing all theoretical physics to the development of a narrow mathematical apparatus - methods for solving the Schrödinger equation. Due to the fact that there was no UNDERSTANDING of the Magnetic Force itself, an ELEMENTARY logical error was made - the Equipotentials of the Ampere Force were taken for the lines of force of the Magnetic Field. Whereas the macroscopic difference between the Ampere Force, which determines the Magnetic Field, and the Coulomb Force lies in the difference in their SYMMETRIES, directly manifested in the degrees of dependence on the distance to the «charge»: inversely proportional to the surface of the sphere for Coulomb and inversely proportional to the surface of the cylinder for Ampere. This directly follows from the fact that the MagneticForce acts not on the Test single charged POINT, but on the Test Line with a single current. And all this Confusion arose from the fact that they DID NOT UNDERSTAND how to describe the observed ASYMMETRY, manifested in the Orthogonality of the Magnetic Force to the Electric Force, determining the Electric Current, while the orthogonality is determined by the fact that, as will be shown below, the Ampere force is reactive, and not static like the Coulomb force. So the MISUNDERSTANDING of the fundamental «details» was simply hidden behind the mathematical formula of the rotor. So they practice, from young Physics enthusiasts to «prominent» theorists, in piling up fantasies.

Coulomb’s Law, as well as Newton’s Law of Universal Gravitation, describes the Static Force. And in the dynamic equation of the Oscillator, they correspond to the Real Members of the equation.

Electrostatic Forces of current carriers in conductors are completely balanced by the charges of the crystal lattice. So Nature itself has identified an additional characteristic of charges moving relative to the observer - the Magnetic Field of conductors, orthogonal to the Electric Field, a measurable Dynamic Force. This allowed us to discover a fundamentally relativistic effect - the Ampere Force. Initially, it was easy to discover a Force proportional to the current and interacting with the Magnetic Force of magnets. So it was understood that the Ampere Force is actually physically connected with the Magnetic Force of magnets. And it was ACCEPTED that the Ampere Force determines the Magnetic Force. But, a strict analysis of this Connection has never been made. And it was not taken into account that the Orthogonality of the Magnetic Force to the Coulomb force is connected precisely with the fact that it is reactive and in the dynamic equation of the Oscillator manifests itself in the form of the Imaginary Member of the equation.

Initially, the Magnetic Force of electric current was introduced traditionally - through Descartes’ drills, i.e. the «Force» ASSUMED around the current, but rotating around it. Whereas from the definition of the Coulomb Force it is clear (Figure 1a) that the specified «orbits» are simply Equipotentials, the gradient of which gives the Ampere Force! This comparison alone is enough to see that (by rotation) they simply tried to express the SIGN of the Force! Indeed, the qualitative difference between the Force of Attraction of parallel currents and the Force of Repulsion of like charges is simply in the SIGN, and not in the direction of rotation:

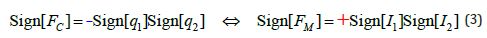
And another difference is that the Equipotentials of the Ampere Force of a linear conductor are not spherical, as for Coulomb, but, as already noted, cylindrical (Figure 2).

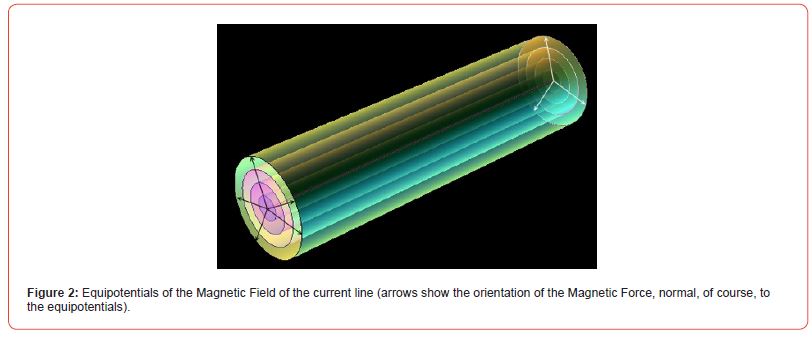
So, the dynamic Magnetic Force applied to cylindrical Equipotentials, being the gradient of the dynamic potential near them, determines the pressure, which decreases inversely proportional to the distance from the current line (the area of the cylinder), in contrast to the static pressure of the Coulomb field, which decreases inversely proportional to the square of the distance from a point charge (the area of the sphere).

Whereas in the traditionally used «Definitions» of the Magnetic Field, what is actually hidden is that at the macroscopic level, it is the Ampere Law for a uniformly moving charge that is the same GIVENESS as the Coulomb Law for a stationary charge:

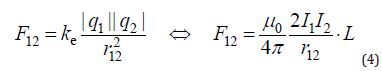
So, Ampere’s Law, as well as Coulomb’s Law, does not require knowledge of the Characteristics of the Field Substructure for its macroscopic description. But the symmetry of the Electric and Magnetic fields is different. If the sources of the Electric Force are, ideally, charges-POINTS, which by their sign set the direction-sign of the force, then the source of the Magnetic Force, ideally, areLINES of current, the direction of which along them sets the sign of the Magnetic Force. In this case, the MEASURABILITY of the Electric Field is determined, ideally, by a point test charge, while the MEASURABILITY of the Magnetic Field is determined by a line of test current of unit length.

And if the Coulomb Force, as well as the Electric Current, are phenomenologically a direct effect of the action of the Electric Force on a stationary/moving test charge, then the Magnetostatic Force described by Ampere’s Law arises as a consequence of the interaction of the current with a unit parallel current

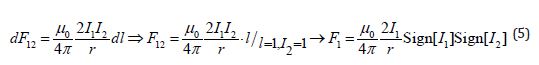
In this case, the Magnetic Force of interaction of conductors is determined by the concentration of electrons in them multiplied by their drift velocity and, in accordance with the Lorentz formula for a single electron, is determined by the RELATIVE velocity of charges in the interacting conductors. And the very existence of the Magnetic Field (Forces) is determined by the relative velocity of charge movement RELATIVELY TO THE OBSERVER. And this applies to both the charges that define the Magnetic Field under study and the charges of the test current. From this it directly follows that the Magnetic Field can interact only with the Magnetic Field! In this case, for two conductors with the same direction of electron current, the Magnetic Forces have the same sign and the conductors are attracted, while the electrostatic attraction of charges of different signs corresponds to Coulomb Forces of different signs!

And since the sign of the current depends on the sign of the charge, then in a closed electric circuit with branches made of semiconductors of different conductivity types, charges of different signs in the branches will move towards each other, but will have Magnetic Forces of the same sign and will be attracted as collinearly moving charges of the same sign. But it should be immediately noted that the Equipotentials of the Ampere Law shown in Figure 2 differ fundamentally from the Coulomb Equipotentials not only in symmetry. Although the Ampere Law, in principle, has the same justification as the Coulomb law - DIMENSIONALITY - inverse proportionality of the Equipotential area, which allows their Forces to be interpreted as a certain pressure (of subparticles), but for Coulomb it is possible to strictly determine by integrating the Force the Electric EQUILIBRIUM Potential

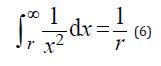
And for the Magnetic Field - a cylinder around a unit length of current, the integral of the Ampere Force is divergent, since this force decreases too slowly with increasing radius. Moreover, the indefinite integral used to determine the cylindrical Magnetic Equipotentials is not equal to the difference in its values at the limits, and at the infinite limit it has no definite values at all:

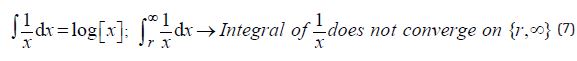
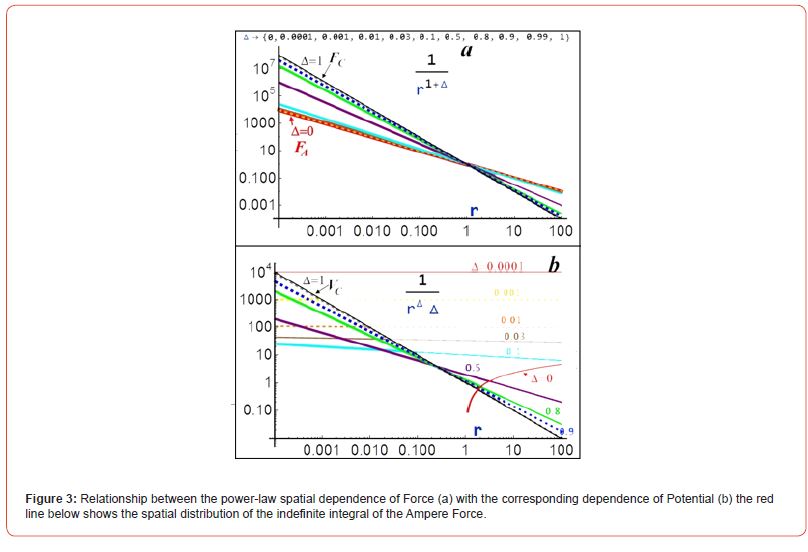
So the conditional convergence of the Magnetic Potential can be obtained only when the degree of the denominator is only greater than one:

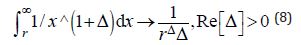
Δ =0, Δ→{0.0001,0.001,0.01,

0.03,0.1,0.5,0.8,0.9,0.99,1}.

JUSTIFICATION The dimension is not strict for Coulomb’s Law [9] either. But its Local character manifests itself only on galactic scales [10].

So it is quite correct to apply the Electric Potential on the microand macro-scales used in Solid State Physics.

Whereas for the Magnetic Field, the spatial distribution of the Magnetic Force allows us to obtain a mathematically correct spatial distribution of the «Potential» only in the limit - when the degree approaches unity. But this «Potential» tending to infinity does not physically correspond to the equilibrium Potential. That is, the Ampere Force integrated to obtain it is not static, it is dynamic - it is a reactive resistance and the Magnetic «Equipotentials» correspond to the POWER of radiation/absorption (and propagation at the speed of light) of the Magnetic Field! It follows from this that for the Magnetic Field, in principle, the empirical rules of Kirchhofffor FLUXES (originally constructed for electric currents) work, and not the Electrodynamics of the theorist Maxwell. After all, if for the Electric Field we can do without the Rule of Continuity of Flows (it is required only for its substructure), then for the Magnetic Field this Rule manifests itself directly.

Magnetic «Induction» B was not introduced into the definitions out of nowhere, but in an attempt to somehow describe the properties of the Magnetic Field. But, by analogy with Coulomb’s Electrostatics, it was only linked, as in Electrostatics, with Magnetic Intensity (in theory with Magnetic Force), supposedly analogous to Magnetic Permeability. But the link was unsuccessful and ambiguous. The latter, as already noted, is not at all analogous to Dielectric Permeability, either when used as a primary external field or as a primary internal field. And the strict correspondence of the noted characteristics of the Magnetic Field to Magnetic Permeability gives only a numerical value and even for a vacuum - ambiguous. As a consequence, there is confusion: «What is the main characteristic of the Magnetic Field: H or B?» is a consequence of the fact that the direction of H was also set incorrectly - in a vacuum it is the same as for B, and not the same as for the Magnetic Force. In this case, as was shown, the main thing was lost - the Reactive Character of the Magnetic Field.

It should be noted right away that the confusion in defining the Magnetic Field also manifests itself at the ELEMENTARY level. That is why the Equipotentials shown in Figure 2 are often taken for lines of force (the lines of force naturally run perpendicular to them along the arrows shown in Figure 2). In order to untangle this Confusion in the ideas about the Magnetic Field, we will conduct a scrupulous comparison of Forces - Electrostatic (Coulomb) and Magnetic (Ampere). Moreover, it is not a fact that the Ampere Force (and after it the Lorentz Force) takes into account all manifestations of the Magnetic Field. In order to UNDERSTAND where this additional characteristic of the Magnetic Field - Magnetic Permeability - came from, we will show what it corresponds to (and does not correspond to) in the characteristics of the Electric Field.

One of the symmetrical differences between the Coulomb and Ampere forces is initially related to the fact that an electrostatic charge of any sign can be considered and described separately, whereas a closed current circuit, in principle, implies the existence of magnetic «charges» only in the form of a pair - a dipole But in order not to miss anything, let us first consider the trivial difference between the LONGITUDINAL Forces of like and unlike electric and magnetic «monopole charges». Using Coulomb’s Law and Ampere’s Law in the form given in formulas 4, but setting all coefficients and «charges» equal to one and taking into account the sign of the force relative to the direction of the spatial axis, we obtain two centrosymmetric, but different in sign, forces shown in (Figure 4).

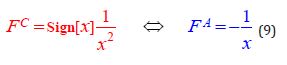
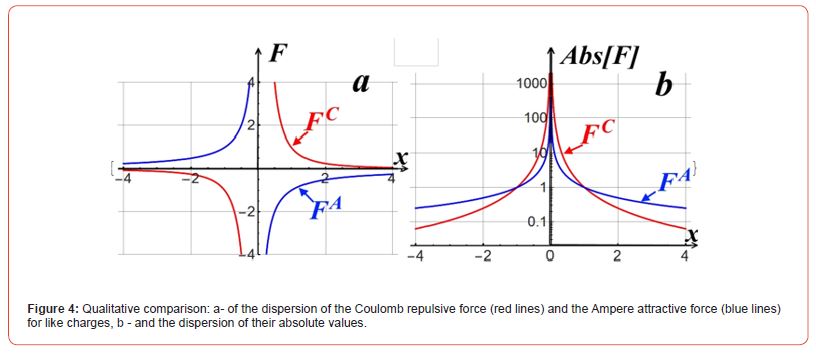
Due to the above-described problems with magnetic reactive potential, we will conduct a comparative analysis of the Magnetism Force with the Electrostatic Force. And the LONGITUDINAL Forces shown in Figure 4 are used further to calculate the TRANSVERSE Forces acting on a single test “charge” between identical charges and unidirectional currents in a plane passing exactly in the middle between them normal to the line (or to the plane) passing through these “charges” - the repulsive force for a Coulomb test charge of the same sign as that of the pair and the attractive force of the test current of the same direction as that of the analyzed pair of single currents.

So, let us first consider the Forces acting on a single test «charge» between identical charges and unidirectional currents in a plane passing exactly in the middle between them, perpendicular to the line (or plane) passing through these «charges». That is, let us consider the repulsive force for a Coulomb test charge of the same sign as that of a pair and perpendicular to the axis of the pair of analyzed charges, and the attractive force of a test current of the same direction as that of the analyzed pair of single currents, perpendicular to the plane passing through the analyzed currents.

Transverse Coulomb interaction of a test charge with a pair of like charges

The well-known Coulomb’s Law can also be used to determine the Force acting, in the simplest case, between a pair of like charges and a test charge. Let’s start with the interaction of this pair with the test charge along the line passing in the middle between the charges of the pair and the perpendicular line passing through the charges of the pair. The Coulomb repulsion force between two like charges and along the axis passing through this pair of charges in the middle between the charges is strictly balanced, and perpendicular to it, naturally, is equal to zero (Figure 5).

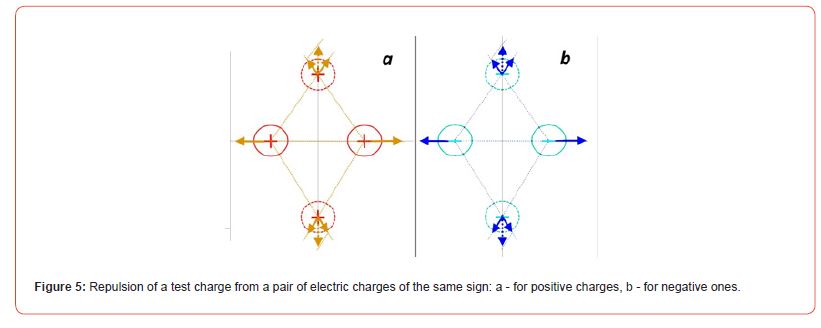
But, as shown qualitatively in Figure 5, when deviating from the axis connecting the charges, the repulsive force of the test charge of the same name and its component perpendicular to the axis first increases, and at infinity decreases as the repulsion from a doubled charge to zero.

For single electric charges, assuming for clarity the distance between the charges and the coefficient also equal to one, we obtain the spatial distribution of the Electric Force perpendicular to the line connecting the charges of the same name:

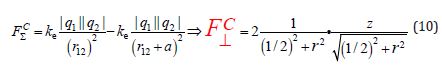
In this case, the Coulomb Repulsion Force between two like charges acts, naturally, not only along the line connecting these charges, but, strictly symmetrically, also on a test charge of the same sign, in the perpendicular direction (Figure 6).

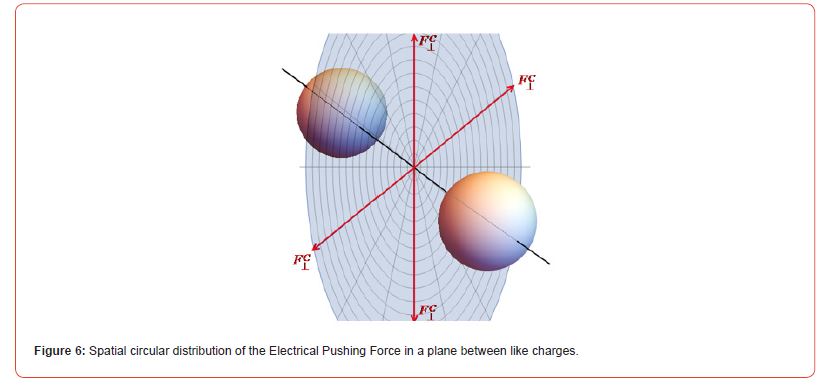
In accordance with formula 9, the Electric Repulsion Force passes through a maximum and decreases symmetrically in all directions along the radius, asymptotically approaching the repulsive force of two charges at infinity (Figure 5).

This repulsive Electric Force, perpendicular to the line connecting the like charges, gives a strictly symmetrical distribution of Equipotentials (Figure 5) and tends at infinity to repulsion from two charges.

So, in accordance with formula 9, the Electric Force of repulsion passes through the qualitatively described maximum above and decreases symmetrically in all directions along the radius, asymptotically approaching the repulsion force of two charges at infinity (Figure 7).

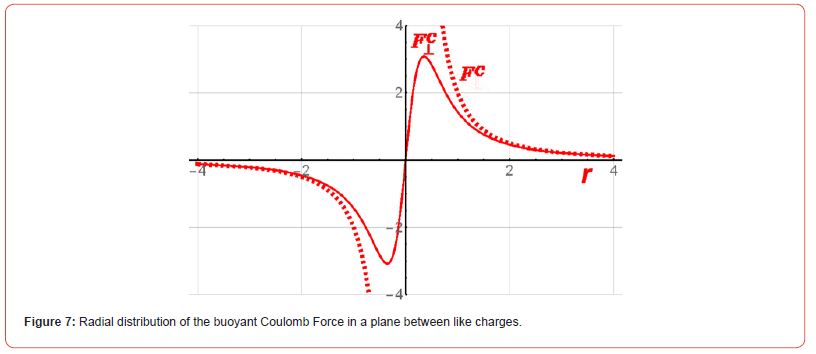
It is also possible to obtain a rigorous expression for the distribution of the Coulomb potential and its equipotentials in the plane shown in Figure 5 (Figure 8).

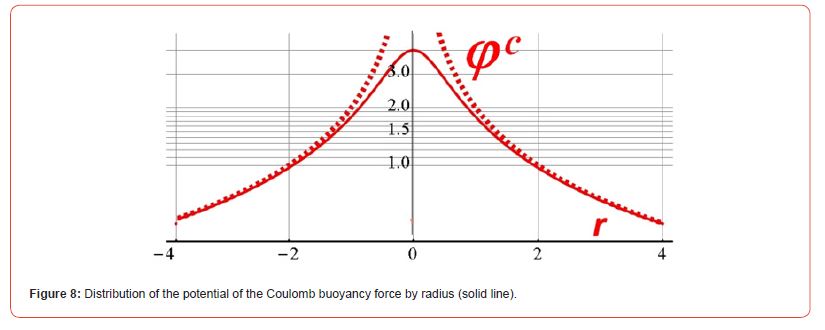
The maximum potential between like charges at the point of equilibrium of the repulsive forces of each charge shown in Figure 7 is precisely the potential barrier that ensures the operation of electronic devices.

If we change the sign of the test charge in Figure 5 to the opposite, then the Coulomb forces will become attractive forces and their dependences on the radius shown in Figure 7 will change sign. In this case, the corresponding distribution of potential will not give the potential barrier shown in Figure 8, but a potential well of similar shape, which is also used in electronic devices.

Transverse interaction of Ampere’s test current with a pair of currents parallel to it

Similar to the above consideration of the Coulomb Force, we will begin the consideration of the Magnetic Force of interaction with a pair of like “charges” - a pair of parallel currents with a collinear test current.

Similar to the above consideration of the Coulomb Force, we will begin our consideration of the Magnetic Force with a pair of like «charges» - collinear currents, parallel and flowing in one direction. The Magnetic Force emanating from the current line (Figure 2) is orthogonal to it in all directions. So in the plane passing parallel to the current lines, and strictly between these currents, it forms a Field of Forces similar to the Coulomb Forces described above, but with some differences. Firstly, like magnetic «charges» do not repel, but attract. Phenomenologically, this field of Magnetic Forces is similar to the field of Coulomb Forces, only Magnetic Forces are defined not as Coulomb forces by spherical Equipotentials, but, as was shown, by cylindrical Equipotentials. Without going into strict justifications of the qualitative conclusions made, for now we will accept these properties of the used Models as an empirical fact that the Magnetic force, although it is dynamic, like any force is a gradient of potential. And, as a consequence of the Ampere Law, the Equipotentials of the magnetic potential form cylinders concentrated around the current line. And the Magnetic Field strength, in ESSENCE, is the Force coming to a unit of «charge», only a unit «charge» is a unit current in a conductor of unit length. So, according to formula 5, it is calculated similarly to the Electric Field strength:

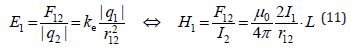
First, let us consider the interaction of a pair of parallel currents with a test current parallel to them.

For Coulomb, as shown in Figures 4 and 5, in a plane perpendicular to the line passing through single charges of the same sign, we obtain a radial PUSHING force, asymptotically tending at infinity to repulsion from two charges, and the Equipotentials corresponding to this force. And it is this force that acts on charges lying outside the plane and is responsible for the connection with orthogonal oscillations even in a non-polar crystal lattice of electric charges, propagating perpendicular to the plane of charges.

Similarly, but taking into account the Sign of the Magnetic Force, we obtain the PULLING Ampere Force normal to the plane passing through the currents (Figure 9).

If we consider the cross-section of two conductors with current by a plane passing through the current lines, then with parallel movement of currents, we will get between the conductors the «tangential» Force of Attraction of Ampere, which lies in the plane tangent to the cylindrical orbitals passing exactly in the middle between the conductors and acting on the collinear test current. This «tangential» Magnetic Force in the plane passing through the currents is completely balanced - zero. And when moving away from this plane, also passing through the maximum, it decreases to zero at infinity. Qualitatively, Figure 9 for current «charges» is similar to Figure 4 for Coulomb charges. But they also have a fundamental difference. If the transition from Figure 4a to Figure 4b–the change of the sign of the Coulomb charges is associated with the violation of the specific Gauge Invariance–with respect to (local)gauge transformations–coordinate-dependent transformations of the field, describing the transition between bases in the space of internal symmetries of this field, then the transition from Figure 9a to Figure 9b with the change of «magnetic charges» is equivalent to the Elements of Spatial Symmetry–either a mirror reflection of Figure 4a from the plane of the figure, or a rotation of the figure by 180 degrees around the line lying in the plane of Figure 9a and connecting the «magnetic charges». In this case, the direction (sign) of the attracting magnetic force does not change (Figure 10).

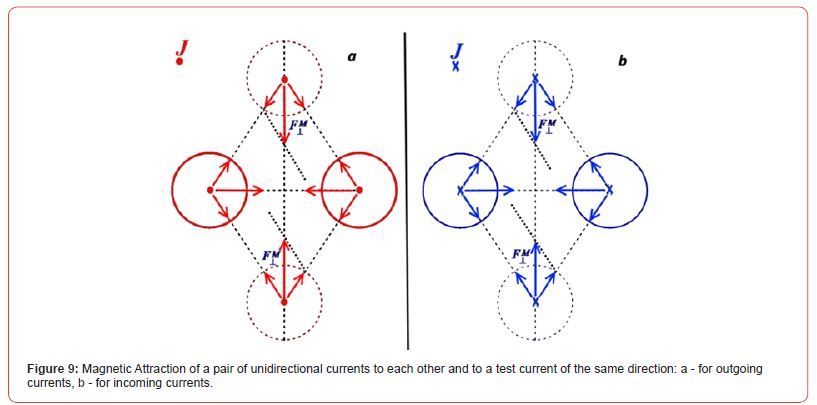
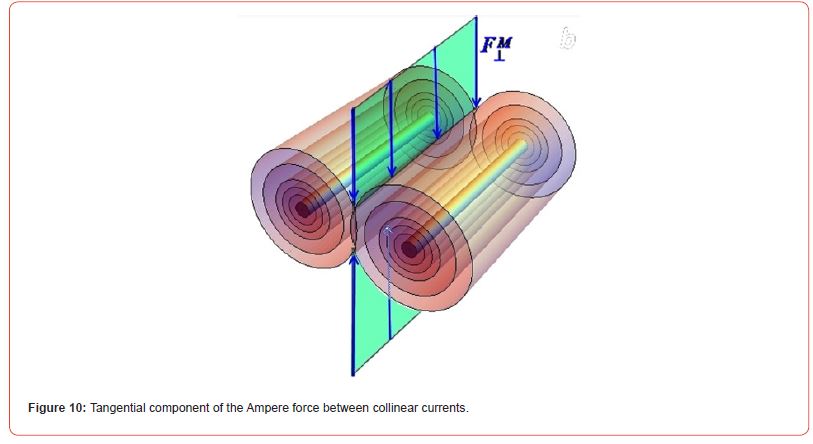
And in connection with the above, it is necessary to immediately note one more Symmetrical Aspect of the Ampere Force of a pair of the same «magnetic» charges. Magnetic Fields, including constant ones, are usually considered/calculated and used for a closed electric circuit, i.e. for counter currents. But if the circuit consists of semiconductors of different conductivity types, then we obtain the same pulling force shown in Figure 9, for which, similarly to expression (9) for the PULLING Coulomb Force, we can also obtainthe distribution of this tangent, PULLING component of the Ampere Force:

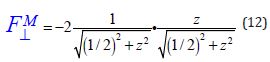
This magnetic transverse SUCTION force has, naturally, the opposite sign to the Coulomb expulsion force. And for a parallel pair, the force becomes, according to Ampere’s law, an attractive force. This attractive force determines the coercive compression of the turns. As shown qualitatively in Figure 10, it is smaller in absolute value than the Coulomb force at the local maximum, but when moving away from the pair of collinear currents, it decreases more slowly than the Coulomb expulsion of like charges. Qualitatively, it is already clear from Figure 10 that, unlike like charges, which create a potential barrier between them (Figure 7), collinear currents «dig out» a similar potential well.

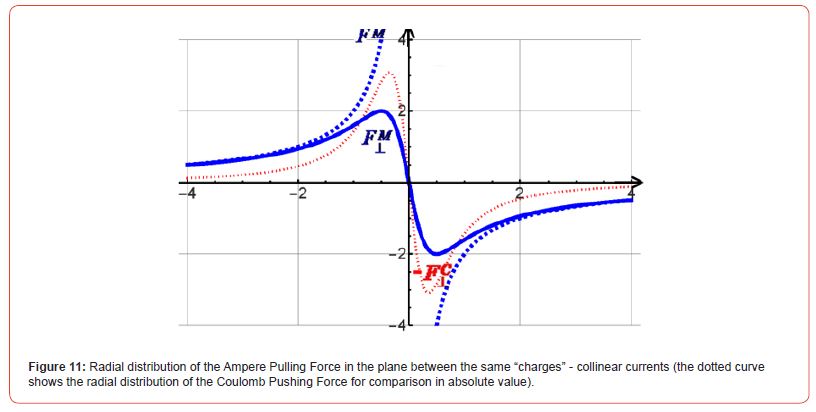
(Figure 11) Radial distribution of the Ampere Pulling Force in the plane between the same “charges” - collinear currents (the dotted curve shows the radial distribution of the Coulomb Pushing Force for comparison in absolute value)

But if “arithmetic” was sufficient to obtain the Stationary Potential from the expression of the Coulomb Force (10), then for quantitative calculations of the Dynamic Magnetic Potential from formula (11), since the Ampere force decreases very slowly (Figure 12), “arithmetic” alone, as was shown in the work, is clearly insufficient.

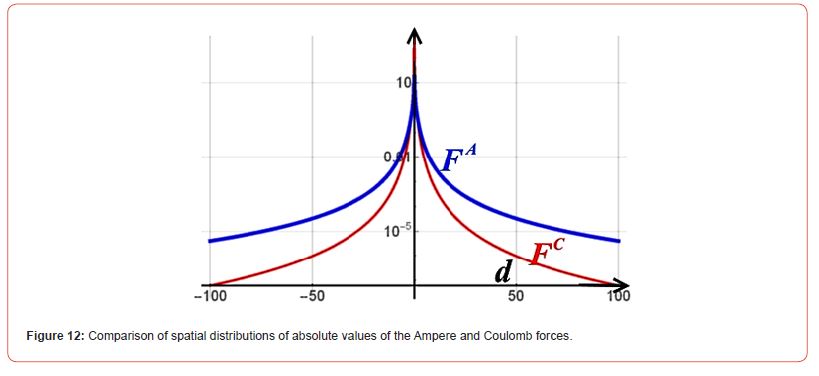
(Figure 12) Comparison of spatial distributions of absolute values of the Ampere and Coulomb forces.

So for now we will limit ourselves to a qualitative, but strict understanding of the Magnetic Force of the same «charges» for a test «charge»: if the test «charge» is of the same sign, a dynamic conditional potential well arises near the plane passing through the currents, but if the test «charge» is of the opposite sign, then a similar barrier of the dynamic conditional potential arises.

Infinity is veiled in the above model calculations of the Stationary Magnetic Potential, the presence of which can be neglected in macroscopic calculations of the Static Electric Potential, but not for the Magnetic Field. The fact is that the Dynamics for Static calculations of Electrostatics, which determines the decrease in Force proportional to the surface of the sphere, is included not at the macroscopic level, but at the level of the substructure of the Electrostatic Field. Whereas the Dynamics of the macroscopic Current of one polarity uses infinity for the very existence of the current of one polarity. For now, we will not go into the connection between the POLARITY of the Current and the POLARITY of TIME, which is necessary for UNDERSTANDING the very emergence of «Descartes’ gimlets», but will only consider their connection in Coulomb’s Law for the Magnetic Field with the Lorentz Force. Coulomb’s Magnetic Law does not include currents (infinite), but magnetic charges (point), for which, as for electrostatic charges, the Law of Inverse Squares of Distance operates. And if we formally take into account the infinity at the ends of the current, which is essential for currents, and calculate the Coulomb Force of the points of an infinite conductor, acting on a given point of another conductor (and on its segment of unit length), then we will obtain the Ampere Force (Figure 13).

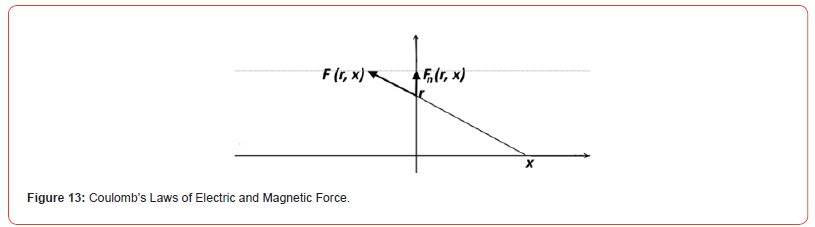
The simplest model shown in Figure 13 makes it possible to understand that the reasoning and calculations given in the first part regarding the quasipotential of the Ampere field contain a similar dimensional error. For both Coulomb’s Electric Law and Coulomb’s Magnetic Law, the Force normal to the thread is determined by all charged points

Whereas the total normal force of action of all points of the line on the test charge decreases inversely proportional to the distance to the line.

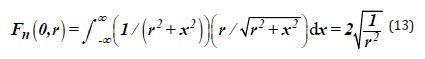
So that the Electric Field Strength forms cylindrical Equipotentials around a charged line, and Coulomb’s Law of Magnetic Force forms cylindrical Equipotentials for an infinitely extended current. So Coulomb’s Magnetic Law is just as valid as Ampere’s Law, just the first one is for the Force at a point, and the second one is for the Force acting on a unit segment of the conductor length. Only Coulomb’s Magnetic Law is for an abstract point moving with the same relative speed as all points of the line (attraction), or with the inverse relative speed (repulsion), and Ampere’s Law is for real measurable currents in conductors of unit length, in which Coulomb’s Electrostatic Law is compensated by stationary charges of the crystal lattice. And the main thing here is that the relative speed of charge movement is RELATIVE to the observer. So this symmetrical difference between spherical and cylindrical Equipotentials is not fundamental, but determined by the conditions of the problem under consideration. Thus, the entire fundamental difference between Electric and Magnetic Equipotentials is determined by the non-zero speed of charge movement for the Magnetic Field. And this determines the Relativism of the Magnetic Field, which also requires additional analysis before considering the transverse dipole interaction.

Einstein, who had a keen sense of the connection between Physics and Reality [11], and when he lost it, did not hesitate to turn to Termen [12] to have him voice the ELEMENTARY GeometricFigures, uttered, in defiance of Schrödinger, a wise phrase: «Some equations of Classical Mechanics allow rewriting in operator form.» And Einstein, in his doubts about Schrödinger’s «Quantum» Calculations, turned out to be absolutely right, since Schrödinger both loosely used Heaviside operators and loose equations of Classical Mechanics [13,14]. But when constructing the Theory of Relativity, Einstein himself became a hostage to both the loose use of Heaviside operators in Electrodynamics by Maxwell and the looseness of the very Concepts of the Magnetic Field in the form of «Descartes’ gimlets.» So, it would seem, the private task of Redefining the Magnetic Field resulted in the Fundamental Problem of modern Classical Physics, which theorists tried to hide behind the «Quantum» MISUNDERSTANDING [14]. Whereas nature, having separated Electric and Gravitational Forces by 42 orders of magnitude, allowed us [15] to supplement Classical Mechanics with the help of the Magnetic Field.

And the given elementary constructions for the effect of collinear and counter currents on the test current, taking into account the Stationary Nature of the Ampere Law, would seem to be enough for an attempt at an axiomatic description of the properties of the Magnetic Field, even for a description of previously unexplored ones. But many BUTs arise!

But, firstly, this ELEMENTARY analysis of single and simplest combinations of like charges shows the complete symmetry of the considered forces, perpendicular to the plane passing through the currents. This is quite natural for the Coulomb forces of monopoles. But the absence of polarity both for the Suction Force between collinear currents, and its natural absence for the zero force between opposing currents already indicates that a simple monopole consideration is not enough to describe the POLARITY of the Magnetic Field.

But, firstly, this ELEMENTARY analysis of single and simplest combinations of like charges shows the complete symmetry of the considered forces, perpendicular to the plane passing through the currents. This is quite natural for the Coulomb forces of monopoles. But the absence of polarity both for the Suction Force between collinear currents, and its natural absence for the zero force between opposing currents already indicates that a simple monopole consideration is not enough to describe the POLARITY of the Magnetic Field.

But, as noted above, a monocycle of the arms of conductors of different types of conductivity also gives a Magnetic Force. Therefore, even oscillations of an electric dipole across its axis at a certain frequency give an ATTENTION magnetic force in the plane between charges for any directions, perpendicular to the axis of oscillation at a double frequency

That is, in fact - a real-measurable, and not a mystical magnetic monopole!

But for a strict symmetrical consideration of the connection of the Ampere Force with the Magnetic Field, it is necessary to analyze magnetic «dipoles» and conduct their scrupulous comparison with electric dipoles. In addition, there is an incomplete, formal account in the description of the Magnetic Field and RELATIVISM. While it is the Magnetic Field that allows us to truly consistently expand Galileo’s Principle of Relativity.

None.

None.

1. Stanislav Ordin (2023) Quantization ESSENCE. Global Journal of Science Frontier Research: A, Physics and Space Science, Global Journals P: 21-29.
2. Stanislav Ordin (2024) Exceptionality Exclusion: Bridging Quantization and Relativity, Global Journal of Science Frontier Research: A, Physics and Space Science P: 5-65.
3. Stanislav Ordin (2024) Reasons for Redefining the Magnetic Field, the Journal of Electromagnetic Analysis and Applications (JEMAA) Scientific Research An Academic Publisher.
4. Stanislav Ordin (2023) Comprehensive Analysis of the Elementary Oscillator", the Journal of Electromagnetic Analysis and Applications (JEMAA).
5. Stanislav Ordin (2024) Foundations of Magnetic Field Definition, Applied Sciences Research Periodicals.
6. Ordin S (2024) Foundations of Magnetic Field Definition. Material Science P: 1-9.
7. Schwinger J Particles Sources. Fields. In 2 volumes. Moscow: Mir. 1973-1976 982 pages.
8. Schwinger J (2018) Particles, Sources, and Fields.
9. Stanislav Ordin (2015) Electrostatic propulsion. Part I, Published on the website of the Nanotechnological Society of Russia.
10. Ordin SV (1965) The Schottky Effect and Cosmos, Global Journal of Science Frontier Research-Physics & Space Science (GJSFR-A) P: 39-50.
11. A Einstein (1965) Physics and Reality”, Science Press, Moscow P: 358.
12. Stanislav Ordin (2014) The Meaning of Life (Dedicated to the Memory of Lev Termen).
13. Stanislav Ordin (2021) Non-Elementary Elementary Harmonic Oscillator, American Journal of Materials & Applied Science (AJMAS) P: 003-008.
14. Stanislav Ordin (2024) Foundations of Quantization, Jenny Stanford Publishing Pte Ltd, 450 P: ISBN 978-981-5129-46-5 (Hardcover), ISBN 978-1-003-57061-5 (eBook). British Library Cataloguing-in-Publication Data, A catalogue record for this book is available from the British Library.
15. Ordin SV (2018) Newton's Coulomb Laws, International Journal of Current Advanced Research P: 1-16.