Selection and Scheduling of Interrelated Alternatives in Transportation Network Development

Good decisions about the selection of projects, options, investments, operating policies or alternative courses of action, and about the timing of their implementation are the essential reasons for the existence of academic and professional fields such as operations research, financial analysis, business management, public administration, engineering economy, decision theory, industrial engineering and project management. In these various disciplines satisfactory methods have been developed for dealing with projects which are not interrelated. For instance, in engineering economics the alternatives are classified as (a) mutually exclusive, (b) independent and (c) interdependent or “interrelated” (Ramakrishna 2010) [1]. The alternatives are considered to be mutually exclusive if only one alternative may be chosen, the others being necessarily rejected. They are independent if the benefits and costs of each alternative do not depend on which other alternatives are selected or when the other alternatives are implemented. If the benefits or costs of alternatives depend on which others are selected and when those are implemented, the alternatives are classified as interrelated. The interrelation becomes more complicated when the benefits and costs of alternatives depend on when the other alternatives are implemented. While generally accepted methods for analyzing mutually exclusive and independent alternatives can be found in textbooks (Sullivan et al. 2018) [2] no such general methods are found for analyzing interrelated alternatives. Furthermore, even the methods that have been designed for analyzing interdependent alternatives in some specific applications have been deficient in their abilities to deal with enough relevant interrelations, uncertainties, scheduling decisions, realistic problem sizes and other important factors.

The lack of adequate methods for analyzing interdependent alternatives is a major gap in the state-of-the-art in operations research, engineering economy, financial analysis, industrial engineering, and related fields. This is especially unfortunate since interdependent alternatives pervade the world. For example, in transportation systems, improvements in a network’s various links and nodes are interrelated partly because such improvements redistribute flows. Each improved link may divert traffic from parallel links, shift congestion and capacity bottlenecks to other links in-series, reduce the need for other improvements, and thus affect the benefits obtainable from improving other network components. Hence, the benefits of various improvements may add up highly non-linearly. Some improvement projects may be synergistic while others may be largely wasted when combined with other improvements, or even counter- productive according to Braess’ Paradox (Steinberg & Zangwill 1983) [3].

Beyond interrelations due to non-linearly additive benefits (including some externalities), alternatives may be interrelated through their costs (e.g., through economies of grouping the construction of several projects), their budget constraints and other financial relations, their constructability or operability requirements, political or equity considerations, and in other possible ways. The proper coordination of improvements to various interrelated infrastructure components (Sun and Schonfeld, 2015) [4] is itself an important and open problem in the technical literature. The term “interrelation” implies a weaker connection than “interdependence”, but the terms are used fairly interchangeably in the literature. The term “dependent” is sometimes used more narrowly to mean “contingent”, i.e., some project requires the acceptance of some other project(s). In addition, decisions regarding infrastructure maintenance or development are subject to substantial uncertainties regarding future demand or usage, costs, finances, implementation times, and future component performance (including capacity, delay, deterioration, and failures). To further complicate matters, large-scale infrastructure projects may be carried out over 10-30 years, which requires that we approach the problem as a multi-period (or multi-stage) decision problem. While methods have been developed for dealing with uncertainties in (multi-period) stochastic capacity expansion and maintenance decisions for infrastructure projects, these are mostly limited to specific applications. This paper summarizes a series of studies conducted at the University of Maryland which developed a more general approach to optimizing the selection, sequencing and scheduling of alternatives or projects for gradually improving various systems. While this approach has mainly been applied to network-based transportation systems, it is applicable to the improvement of other kinds of infrastructure and systems, such as, utilities, communication systems, production facilities and public services.

Planning and scheduling projects are major aspects of many business and engineering applications. In practical settings, the decision makers have to (1) allocate limited resources to multiple candidate projects (which is called resource assignment, or project planning/selection), and (2) decide the starting/ending times for each selected project over a time horizon (called scheduling), so as to optimize some performance metric (e.g., maximize net present value or expected profit). Joint resource assignment and project scheduling are challenging from a computational perspective (Lombardi & Milano 2012) [5] even if the projects are not interrelated and if no uncertainties are considered (Hartmann & Briskorn, 2010) [6]. However, almost any transportation network improvement involves interrelated projects, as demonstrated through the following examples.

Waterway Lock Improvement Projects (as in Fig. 1) or major maintenance projects are interrelated since delays at one lock are affected by operations at many other locks, both upstream and downstream. Expansion at one location may shift delays and capacity bottlenecks elsewhere, as analyzed in Wang & Schonfeld (2005 and 2008) [7,8]. These inter-dependencies may be evaluated via microsimulation (Wang et al. 2009) [9] or a metamodel (Dai & Schonfeld 1998) [10], both of which may require extensive computational effort to evaluate a single candidate solution over a long analysis period. Hence, evaluation of numerous candidate solution greatly benefits from parallel computations (Yang et al., 2015) [11].

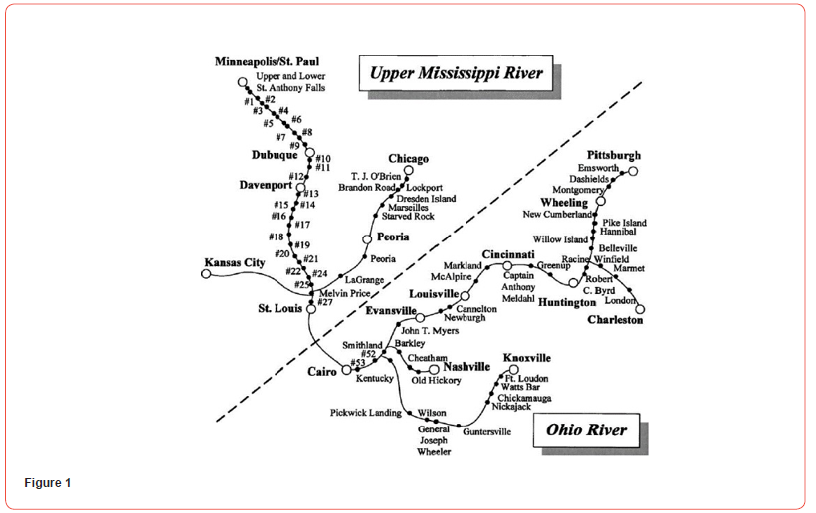
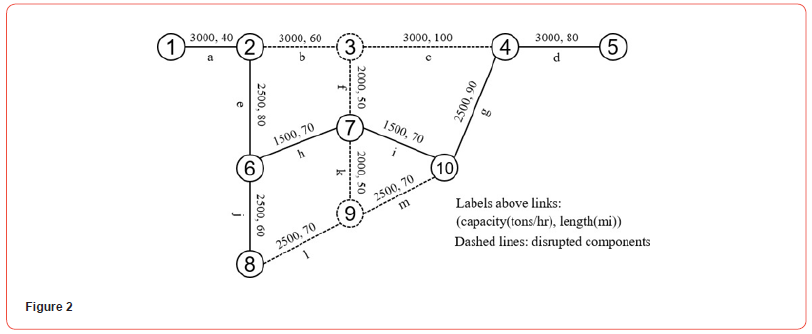
Restoration of a Railway Network after damaging events is sometimes needed. Under normal operations, freight flows between origin-destination pairs are optimally assigned to different paths to minimize the total hourly cost under linkcapacity constraints. However, network operation is occasionally disrupted due to system or human-induced failure, which results in reduced capacities of multiple links in the network. We must find the best restoration schedule for damaged components, while accounting for re-routing, mode shifts (e.g., to trucks), storage costs and various uncertainties that may arise in such projects (e.g., stochastic restoration time, demand after the impact). Here, in order to evaluate a candidate solution, we must repeatedly solve a minimum cost network flow model, possibly with storage queues. Such problems have been analyzed and solved by Wu et al. 2022 [12] and by Ng and Schonfeld 2022 [13]. Wu (2023) [14] integrated short-term post-disruption restoration with long-term network resilience improvement in a tri-level optimization model, with flow re-routing at the lower level, short-term restoration at the middlelevel and long-term restoration at the upper level.

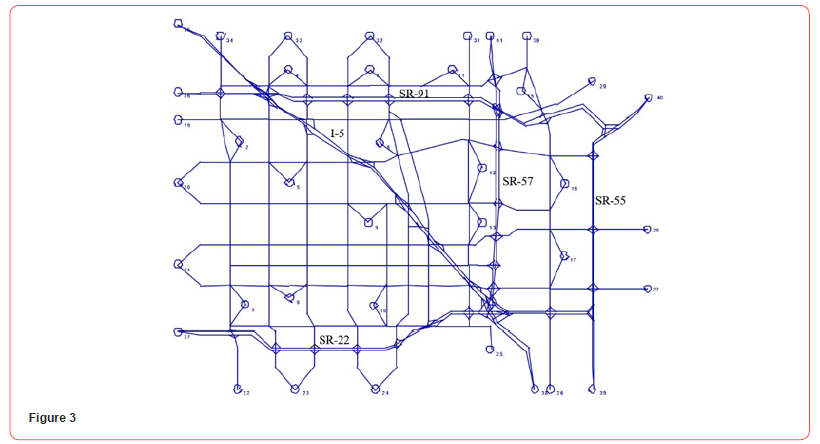
Capacity Expansion of an Urban Road Network is another example. Existing links may be widened, with possibly cyclical re-allocation of lanes (e.g., to mixed traffic, buses, high-occupancy vehicles, bikes, sidewalks, on-street parking), intersections can be expanded along with traffic control changes, and new links may be added, all during a long development period. Thus, Jovanovic, et al. (2018) [15] jointly optimized intersection and link improvements, while Shayanfar & Schonfeld (2019) [16] optimized network development under probabilistic demand using a cell transmission model in evaluating the relatively large Anaheim network (Figure 3).

An early work on interdependent alternatives was that of Markowitz (1952) [17] on portfolio management. Dickinson, et al. (2001) [18] developed a model for optimizing a set of development projects for the Boeing Company. The authors used a dependence matrix to quantify the interdependencies among projects and a non-linear, integer program to optimize the project selection. However, the use of a dependence matrix is hardly satisfactory, especially for large problems. As noted by Disatnik and Benninga (2007) [19], the estimation and processing of a dependence matrix becomes computationally difficult as the project space grows. More importantly, the pairwise and n-way dependencies do not completely represent the complex interrelations among alternatives. Instead of a dependence matrix, complete system models, such as queueing approximations (Jong and Schonfeld, 2001) [20], equilibrium assignment (Tao and Schonfeld, 2005 and 2007) [21,22], microsimulation (Wang and Schonfeld, 2008) [8] and neural networks (Bagloee and Tavana, 2012) [23], are better suited for modeling complex interrelations, especially in large network-based systems.

A generally applicable framework for optimizing the selection and scheduling of alternatives in system development problems has been pursued through a series of studies at the University of Maryland. Its basic concepts are described below.

The problem, which has very wide range of applications, includes the following steps:
1. Identify and specify a list of alternatives. Some internal optimization may be employed in specifying the alternatives. The alternatives may differ greatly in their nature. For example, transportation system alternatives may include construction of new components, expansion of existing components, maintenance, changes in operation and control policies, pricing and other incentives.
2. Evaluate complete systems over entire analysis periods. This may be done with existing methods or newly developed ones, such as analytic optimization models for rail transit (Wu and Schonfeld, 2022) [27], equilibrium traffic assignment for road networks (Jovanovic et al., 2018; Shayanfar and Schonfeld, 2019) [15,16], cell transmission models for road networks [24], and microscopic simulation for waterways (Wang et al., 2009; Wang and Schonfeld 2012) [9,25]. These methods evaluate the system’s performance as new alternatives are introduced (and possibly removed) at specified times (according to step 5) over an entire analysis period, which may range from hours (for short-term restoration problems) to decades (for longterm network improvement). Thus, the interrelations among alternatives introduced and removed at different times are captured by the complete system evaluation model, which computes performance measures, such as net present value, for the whole system over the entire analysis period.
3. Optimize the entire development schedule. This step integrates the selection, sequencing and scheduling of changes in the system. While many different optimization methods may be mixed and matched with the evaluation method used in Step 2, we usually employ a genetic algorithm to generate candidate sequences of alternatives to be evaluated. A sequence is translated into a precise schedule over continuous time by applying relevant binding constraints. The available budget flow over time is usually the dominant constraint determining when successive alternatives in a sequence can be implemented. Externally sourced budgets may be supplemented by revenues generated internally by the original system and previously implemented alternatives. Even if budgets suffice, alternatives in sequences may be delayed until demand levels, benefit cost ratios, or other constraints are satisfied.

The optimization algorithm generates candidate sequences of alternatives and evaluates them by using the method in Step 2 as a subroutine to evaluate its objective function (e.g., profit or net present value). It refines the sequences iteratively (e.g., through multiple generations of a genetic algorithm) until a convergence criterion is satisfied. In addition to genetic algorithms, simulated annealing and tabu search have been tested and compared, among other optimization methods (Shayanfar et al., 2016) [26]. Since computation requirements increase considerably with problem size, population-based algorithms such as genetic ones, are especially suitable since they can easily distribute to parallel processors the individuals from populations or replications of probabilistic evaluations.

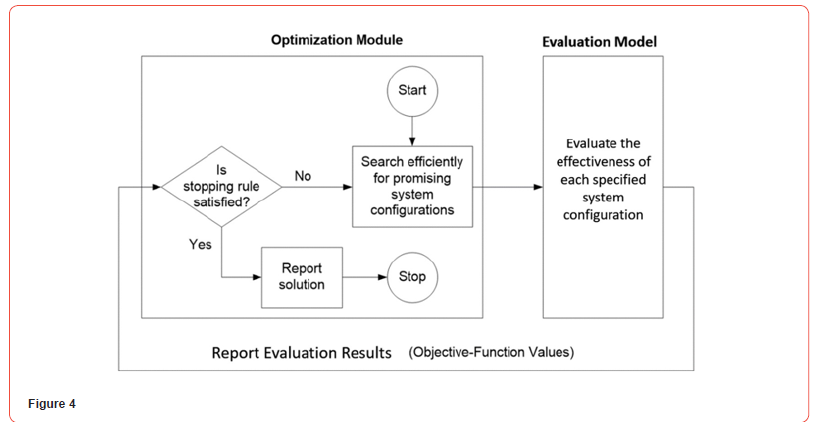
A key aspect of this framework is that the evaluation method (Step 2) and optimization method (Step 3) are separable, as indicated in the following figure from Shayanfar [24] (2018). Various evaluation methods can be and have been combined with various optimization methods with minimal connectivity problems. The optimization method is very generally applicable to problems of selecting interrelated alternatives in various domains (far beyond transportation networks), while the evaluation method is problem-specific.

This framework has been extended to deal with uncertainties. For example, Shayanfar [24] (2018) treats uncertainties regarding future demand by optimizing network development schedules based on probability distributions. Wu (2003) [14] deals with multiple uncertainties, including correlated uncertainties, regarding future demand, costs, and budgets. The results obtained with this framework are documented in multiple journal papers and Ph.D. dissertations, some of which are listed in the references.

The framework discussed here has many potential applications in many fields, which can be pursued by researchers with specialized knowledge in those fields. At the University of Maryland, current research focuses on (1) optimizing multi-modal public transportation systems and (2) integrating road space allocation (e.g., among mixed traffic, bus lanes and bicycle lanes) with network evolution. Fairly large problems can already be solved on current laptop computers. For example, Shayanfar (2018) [24] solved the Annaheim network (616 nodes and 914 links) with 100 projects in 18,533 cpu seconds. However, for much large and more complex problems, especially with stochastic aspects or detailed optimization of each alternative, computational improvements are desirable. These may include extensive parallel processing, new and hybrid algorithms, and extrapolation from intermittent microsimulation.

“The author is grateful for the contributions to the described methods of several doctoral students, including Jyh-Cherng Jong, Shiaaulr Wang, Xianding Tao, Elham Shayanfar and Fei Wu.”

None.

1. Ramakrishna K (2010) Essentials of Project Management. PHI Learning Pvt. Ltd.
2. Sullivan WG, Wicks EE, Koelling CP (2018) Engineering Economy (17^th Edition), Prentice Hall.
3. Steinberg R, Zangwill WI (1983) The Prevalence of Braess' Paradox". Transportation Science 17(3): 301.
4. Sun Y, Schonfeld P (2015) Stochastic Capacity Expansion Models for Airport Facilities. Transportation Research Part B: Methodological 80: 1-18.
5. Lombardi M, Milano M (2012) Optimal methods for resource allocation and scheduling: a cross-disciplinary survey. Constraints 17(1): 51-85.
6. Hartmann S, Briskorn D (2010) A survey of variants and extensions of the resource-constrained project scheduling problem. European Journal of Operational Research 207(1): 1-14.
7. Wang SL, Schonfeld P (2005) Scheduling interdependent waterway projects through simulation and genetic optimization. Journal of waterway, port, coastal, and ocean engineering 131(3): 89-97.
8. Wang SL, Schonfeld P (2008) Scheduling of waterway projects with complex interrelations. Transportation Research Record: Journal of the Transportation Research Board 2062(1): 59-65.
9. Wang SL, Yang N, Schonfeld P (2009) Simulation-based network maintenance planning and scheduling. Transportation Research Record: Journal of the Transportation Research Board 2100(1): 94-102.
10. Dai MD, Schonfeld P (1998) Metamodels for estimating waterway delays through series of queues. Transportation Research Part B: Methodological 32(1): 1-19.
11. Yang N, Wang S, Schonfeld P (2015) Simulation-Based Optimization of Waterway Projects using a Parallel Genetic Algorithm. International J. of Operations Research and Information Systems 6(1): 49-63.
12. Wu F, Schonfeld P, Ayyub B, Kim M (2022) A Topological Approach for Optimizing Railroad Freight Network Restoration after Disruptions. Transportation Research Record 2676(12): 750-759.
13. Ng M, Schonfeld P (2023) Sequencing Interdependent Transportation Network Improvement Projects: Exact Solution Method via Network Flow Reformulation. Transportation Research Part D: Transport and Environment 115: 103565.
14. Wu F (2023) Selection and Scheduling of Interrelated Network Improvement Projects under Uncertainties. Ph.D. Dissertation, Univ. of Maryland, College Park.
15. Jovanovic U, Shayanfar E, Schonfeld P (2018) Selecting and Scheduling Link and Intersection Improvements in Urban Networks. Transportation Research Record 2672(3): 1-11.
16. Shayanfar E, Schonfeld P (2019) Selecting and Scheduling Interrelated Road Projects with Uncertain Demand. Transportmetrica A: Transport Science 15(2): 1712-1733.
17. Markowitz H (1952) Portfolio selection. The Journal of Finance 7(1): 77-91.
18. Dickinson MW, Thornton AC, Graves S (2001) Technology portfolio management: optimizing interdependent projects over multiple time periods. Engineering Management, IEEE Transactions on 48(4): 518-527.
19. Disatnik DJ, Benninga S (2007) Shrinking the covariance matrix. The Journal of Portfolio Management 33(4): 55-63.
20. Jong JC, Schonfeld P (2001) Genetic algorithm for selecting and scheduling interdependent projects. Journal of waterway, port, coastal, and ocean engineering 127(1): 45-52.
21. Tao X, Schonfeld P (2005) Lagrangian relaxation heuristic for selecting interdependent transportation projects under cost uncertainty. Transportation Research Record: Journal of the Transportation Research Board 1931(1): 74-80.
22. Tao X, Schonfeld P (2007) Island models for stochastic problem of transportation project selection and scheduling. Transportation Research Record: Journal of the Transportation Research Board 2039(1): 16-23.
23. Bagloee SA, Tavana M (2012) An efficient hybrid heuristic method for prioritising large transportation projects with interdependent activities. International Journal of Logistics Systems and Management 11(1): 114-142.
24. Shayanfar E (2018) Planning and Prioritizing Interrelated Road Network Projects by Integrating Cell Transmission Model and Genetic Algorithm. Ph.D. dissertation, Univ. of Maryland, College Park.
25. Wang SL, Schonfeld P (2012) Simulation-based scheduling of mutually exclusive projects with precedence and regional budget constraints. Transportation Research Record: Journal of the Transportation Research Board 2273(1): 1-9.
26. Shayanfar E, Abianeh AS, Schonfeld P, Zhang L (2016) Prioritizing Interrelated Road Projects Using Meta-Heuristics. Journal of Infrastructure Systems 22(2): 04016004.
27. Wu F, Schonfeld P (2022) Optimized Two-directional Phased Development of a Rail Transit Line. Transportation Research Part B: Methodological 155: 424-447.
28. Jong JC, Schonfeld P (2003) An evolutionary model for simultaneously optimizing three-dimensional highway alignments. Transportation Research Part B: Methodological 37(2): 107-128.