Russian Cosmism for Euclidean Matterspace with Nonlocal Communication

Aristotle’s space-plenum was material and self-governed by elastic properties [1]. Everything in such a material space has reasons, which together explain the existing order in the organisation of the mechanical world of inertial bodies. The concept of regions of empty space without matter was also unclear to Descartes [2,3], who considered the continuous extension of matter or ‘matter-extension’ to support Plato’s ether-extension of bodies and Aristotle’s non-empty space-plenum. Newton’s successful dynamics of localised masses with inelastic exchange masked for a time the need for elastic non-locality and Cartesian matter-extension with sophisticated vortex grids. Today, Newton’s dualism of massive particles and massless forces in empty space has led to the Standard Model of Physics, where particles and their interaction fields are two basic concepts. Not Aristotle’s space-plenum or Cartesian material space, but Newton’s empty space modelling became mandatory for the weak field limit in Einstein’s tensor gravity since 1915.

Today, scientific reviewers have established that Einstein’s metric gravity, in the limit of small velocities, fields and pressures, must be reduced [4] to Newton’s dualistic theory, which divides matter into two independent concepts - isolated bodies in the void and massless force fields for assumed interactions between such bodies or massive particles. The Newtonian view of the fundamental nature of the interaction forces is supported by the collective efforts of international collaborations seeking to explain all observed phenomena without deviating from the CERN model of paired interactions between elementary hierarchies or quantum particles. Anything that contradicts the concept of interaction for supposedly observable partners is not published because of the risk of losing the reputation of the journal and its reviewers.

The successful application of the dualistic worldview to the testable mechanics of dissipative exchange rejected the Eastern doctrines of the holism of the material world. The elastic organisation of non-locally distributed masses began to be sophisticatedly explained on the basis of inelastic models of Newtonian mechanics for forced laboratory accelerations, even at the cost of Euclidean space. The idea of a single whole acting on its own matter is at odds with the model’s notion of interactions. There are no partners in a holistic organisation, and there is no interaction at all in this philosophical approach to observed gravity, for example. Dualistic physics for paired interactions and energy exchanges fails to calculate gravitational self-action due to the self-energy divergence for the Newtonian-Euler point mass. Inellastic exchange between quasi-elastic hierarchies is only a part of non-local physical reality with continuous matter-space. And mechanical theories without elastic mechanisms for long-range self-regulation of such etheric matter-space with visible (dense) and invisible (rarefied) regions are incomplete.

There is no doubt that bodies visible in the laboratory can exchange energy through mutual inelastic collisions and can change their energy under the action of external forces according to the laws of Newtonian mechanics. But in constant gravitational fields, the energy of a probe body does not change. And in the phenomenon of gravity, the idea of local exchange between partners should give way to the idea of holism in the non-local distribution of the unified whole. Not being able to go into details of foreign holistic concepts, I will propose for astronomical observations the doctrine of Russian Cosmism about monistic unity of the world with inseparable unification of living and cosmic matter by V. I. Vernadsky [5] on the universal basis of Euclidean space of naturalists.

In Russia, Mikhail Lomonosov categorically did not accept Newtonian pulls through the void ‘from there to here’ and from 1742 insisted on local pushes of observable bodies by unobservable (etheric) matter fluid ‘from here to there’ [6]. This anti-Newtonian approach allowed Lomonosov to propose the later confirmed mechanism of bioimpulses in nerve fibres and even to lay the physiological foundations of vision. Local self-acceleration of visible matter due to elastic stresses of the etheric medium is not related to dissipative collisions of particles and other inelastic processes, as in Newton’s dual mechanics of energy exchange. Lomonosov’s elastic gravitation does not lead to overheating or burning of planets in Keplerian orbits, unlike the kinetic models of gravitation of Fatio (1690) and Lesage (1756). The inelastic mechanical exchange between the corpuscular ether and the planets was rightly criticised by Maxwell because of the inadmissible heat, and by Poincaré because ultra-mundate corpuscles require superluminal velocities.

Lomonosov’s baton about the continuous ether as an elastic medium of liquid type was supported by another Russian cosmist, Nikolay Umov [7], who related the mass of observable bodies to their etheric filling. In 1873 he introduced the vectorial concept of energy density transfer. There, volume integrals of the internal mass-energy k(v²)mc² in free fall released for accessible measurements Newton’s kinetic energy, mv²/2=k(v²)mc² In the relativistic generalisation of Umov mechanics with ether degrees of freedom for the hidden kinematic mass energy, the coefficient k (v ^ 2) coincides with the Lorentz factor, 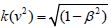which gives ether physics full compatibility with the Lorentz transformations [9] under an elastic spectrum of internal energies 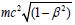on Keplerian ellipses.

With the continuous filling of space by the ether mass-energy of Umov, it makes sense for relativists to think about the field state of such an extended mass and about nonlocal mechanisms of its space-time self-organisation. One perspective approach is the geometrization of the field mass as a physical alternative to Einstein’s geometrization of empty space [9]. Another approach is the introduction of information fields [8] into the extended mass-energy for the self-regulation of internal stresses and self-accelerations of the non-local hierarchy. In the relativistic theory of the monistic unity of field matter, both such approaches lead to the same mathematical relations for elastic self-actions. Manifestations of local self-action without time delay are used in Russian Cosmism for astronomical observations instead of imaginary fundamental forces in Newtonian long-range interactions with required light retardation.

The nonlocal hierarchy with elastic mechanical properties and Shannon entropy can be modelled as spatial superpositions of lighter hierarchies with small mutual exchanges of energy and information. These wave exchanges represent dissipation for the motion integrals of the quasi-ellastic hierarchies. For small inelastic perturbations of metric information distributions, the referents of Newton’s dual physics are in demand, because even galaxies can be simplified by a point mass at the centre of gravity in the 2nd law of classical acceleration due to energy exchange. The minimum number of new model objects when breaking up a closed holistic system is not two but three (Father, Son and Holy Spirit in the Russian Trinity), since lighter hierarchies are no longer closed and require the introduction of exchange fields or interaction forces. Without dissipation there would be neither the evolution of quasi-stable formations nor their observation. Elastic-nonlocal states and local dissipative processes are equally important for the phenomena observed in the continuous matterspace without voids. It is important for physics and astronomy to avoid conceptual substitutions leading to unnecessary conflicts between monistic unity and simplified dualistic interpretation of macrocosm and megacosm with instantaneous elastic stresses and inelastic wave processes with time delay.

The non-Newtonian geodetic precession of the asymmetric Earth-Moon gyroscope in the gravitational fields of the Sun was first noted by de Sitter [10] in 1916. The modern quantitative analysis of the Lunar Laser Ranging (LLR) data collected by NASA between 1970 and 1986 was finally published in 1988 [11]. These data were interpreted in terms of the post-Newtonian metric parameter γ, related to the supposed departure of 3D space from Euclidean flatness. The curvature of empty space should inevitably accompany the point-source models used by Schwarzschild in the 1916 solutions [12] to Einstein’s 1915 equation. It is now agreed that the energy-momentum tensor density, rather than the point mass, is a real source of General Relativity (GR) fields in this nonlinear gravitational equation for classical particles. From here, the radial field energy density, 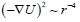acts as a non-local r^-4material source of metric fields. In other words, realistic space-time-energy organisations in Einstein’s universe cannot, in principle, operate with the empty (or free) space paradigm, because the GR energy source, together with its testable field, is distributed over non-empty space, which is everywhere filled with inseparable mass-energy.

Nevertheless, the numerical agreement (2% experimental error in 1988 [11] and 0.7% in 1996 [13]) of measurements with the Schwarzschild parameter γ = 1 for the pre-quantum point particle was accepted by NASA researchers as the ultimate proof of the curvature of space, driving the flat-space advocates out of the major gravitational conferences. Sommerfeld, Brillouin, Schwinger and many other classics had already explained the conceptual role of Euclidean space for modern physics. Feyman even insisted on registering for conferences under a pseudonym (e.g. 1957, Chapel Hill, NC). Einstein [14] and others [15,16,17] criticized metric singularities, but the black hole generation of cosmologists persistently ignore the `irrelevant’ criticism of their `reluctant father’.

The experimental data of the Gravity Probe B (GPB) mission [18,19] could be readily accepted by the Schwarzschild-Schiff model with 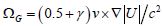for the geodetic precession frequency of four-vector spins without radial structures in locally curved space [20]. The superficial modelling of (distributed) classical bodies by point masses in empty space prevents the timely recognition of the GPB breakthrough – 3-dimential space is strictly flat (better than 1%) with respect to translations and rotations. The point is that the GPB data (einstein.stanford.edu) for small superconducting gyroscopes replicate the same geodetic precession of the well-studied Moon-Earth gyroscope. This distributed system has been described quantitatively without point singularities. Its slow-motion precession in Einstein’s theory of relativity is related to the inhomogeneous time dilation over the lunar orbit and not to the assumed curvature of space at the centre of inertia of the gyroscope.

Recall that Weyl submitted his correct calculations for nonpoint relativistic tops in 1923, long before the Einstein-Infeld-Hoffmann equation [21] of slow relativistic motion was derived in 1938. And the classical Lagrange formalism for Einstein-Infeld-Hoffmann dynamics very clearly specifies the enhanced geodetic precession of non-point orbiting gyroscopes by the GR time dilation or oo g metric component [22]. Why was the known time dilation nature of the de Sitter - Weyl - Einstein - Infeld - Hoffmann geodetic precession never mentioned by the NASA researchers as an original GR alternative to their curve-space interpretations? Einstein never abandoned his 1938 post-Newtonian dynamics of distributed passive-active elements and tried to introduce extended (non-point) gravitational sources even into the 1915 covariant equation. Initially, Einstein and Grossmann put the Newtonian potential U = −GM r only in the time subinterval of the Minkowski space-time interval [23]. More recently, Schwarzschild’s point-source constructions reconnected both time and space subintervals with the gravitational potential. This mathematical model for dualistic masses and massless fields badly redirected the Einstein-Grossmann metric project into the classical framework of pre-quantum physics with empty space. Grossmann did not agree with the curved 3-space and abandoned his further collaboration with Einstein.

Again, why were very clear anti-Schwarzschild statements of Einstein never cited by NASA researchers of `Einstein’s Universe’? Unrealistic point sources or spins are sometimes very useful for simplified, model-like interpretations of physical reality. But they should not replace or eliminate more rigorous pro-Einstein approaches to the self-organisation of matter-space-time in the nonlinear GR equations with non-local energy charges or with non-empty space [9,24]. NASA reports cannot ignore Einstein-Infeld- Hoffman physics for slowly rotating mass-energy distributions in favour of Schwarzschild-Schiff mathematics for point particle- spin, which is a model simplification. What are the reasons for modifying Einstein’s 1938 physics [21] before gravitational tests?

In the alternative view of Russian cosmists, NASA’s LLR and GPB public releases have perfectly confirmed GR’s time dilation in the Einstein-Infeld-Hoffmann approach to distributed GPB gyroscopes, but without any unphysical contributions from non-existent spatial curvature. There is no need to reinterpret the classical GR rotation by point-spin innovations. One could propose to keep the 1923 Weyl-Einstein non-point gyroscope and compare the `entwurf’ flat-space generalisation of the Minkowski interval [23] with the LLR and GPB data for spin-orbit and spin-spin frame-dragging. And one can call for a non-empty space interpretation of metric physics for the global Machian overlap of r⁻⁴ nonlocal matter in the Euclidean universe [8]. Purely field masses quantitatively describe all measured gravimetric corrections to Newtonian theory without departing from Euclidean space geometry [24]. The world monism of Tsiolkovsky and other Russian cosmists (Lomonosov, Umov, Vernadsky, Chizhevsky, Vlasov, Kozyrev) would be beneficial for separating the realistic Einstein heritage from point-mass simplifications and naive empty-space models.

It is useful to recall the dualistic scheme of derivation of Einstein’s field equation on the basis of the traditionally accepted model of point masses in empty metric space describing pairwise interactions. In the autumn of 1915, Einstein began to equate the tensor densities G_μν at the mathematical stresses of geometrised spacetime with the 10-component energy tensor for matter T_UV=T_VU Indeed, it was thought at the time that the dual scenario of equality of vector densities for the electromagnetic field and the electric current worked well for interpreting Maxwell’s electrodynamics. Nothing else but the proportionality of the properly chosen field tensor G_μνand matter tensor T_UV can offer the dual splitting of matter into massless field and inertial particles. The tensor of classical matter has been proposed to be written out by known methods with the help of corresponding derivatives for massive densities in the Lagrange formalism, i.e. without geometrization of massive sources. The final field tensor 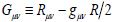for geometrized space time was initially described by the author of GR with only the first summand, the symmetric Ricci tensor R_UVAnd finally (after communications with Hilbert), Einstein began to add to his field tensor G_μν the second summand 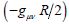with the scalar convolution of the Ricci tensor by the metric tensor,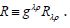

The new variational equation, 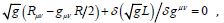in Hilbert’s first communication [25], corresponded to the Einsten tensor update [26] for gravitationa1 iterations in 1915: 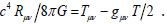Using 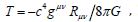Einstein rewrote his December the 2d equation in the Hilbert equivalent form, 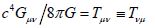. It takes ten independent components and allows empty regions of space with zero matter density. In the void, it is necessary to set 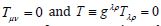in the sense of the dualistic concept of matter. In empty regions, the dual ideology of GR did not object to the independence of all ten components of the symmetric tensor g^μν in the Hilbert variations of the field action integral.

By the general relations of pseudo-Riemannian geometry for the Ricci curvature Rμν , all ten components of the metric space-time tensor G_μν can be involved in the ten requirements R_UV=R_UV=0 corresponding to the degenerate for the empty Einstein equation. These exaggerated, according to the proponents of flat space, requirements led Karl Schwarzschild to the famous solution 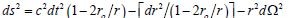(where 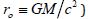for an invariant 4-interval ds . There is no mathematical error in this metric solution with a curved three-dimensional space around a massive point (or metric singularity). Concerns can only be made about Einstein’s Equation, not about its exact solution. In 1916, Einstein presented the Schwarzschild metric to the Prussian Academy of Sciences as a reference solution of his tensor equation for strong and weak metric fields from a static source - Newton’s massive point at the origin.

It was not until the 1930s that Einstein reconsidered his initial support for the mathematically flawless Schwarzschild metric. Singularities at the origin of the coordinates could not withstand the reasoned criticism of the great thinker. In 1939 a thought experiment [14] led to impermissible superluminal rotations of test bodies in a strong field near a singularity. And no one has yet been able to refute this concept-breaking experiment. Having accepted the Schwarzschild metric for weak-field problems, Einstein categorically rejected it for the strong-field limit because of its physically absurd results. He began to lean towards reorganising the dual equation of 1915 on a non-dual basis. After all, quantum mechanics works successfully with a monistic distribution of mass throughout space.

“Can’t we abandon the concept of substance and build a pure field physics? What acts on our senses as substance is in fact a huge concentration of energy in a relatively small space. We could consider matter as such regions in space where the field is extremely strong. In this way the foundations of a new philosophy could be established. ... a thrown stone is a changing field in which the states of greatest field intensity move through space at the speed of the stone. In our new physics there would be no room for both field and matter, since the only reality would be the field. ... Our main challenge would be to modify the field laws so that they are not violated for regions in which energy has enormous concentrations. The conclusion as to whether such a program is possible belongs to the future”. In these well-known statements about the prospects of field physics, Einstein and Infeld [27] proposed to move away from the dualistic world view with massive partners in the void towards the Cartesian world order based on a monistic distribution of field mass with large and small densities throughout space. The development of relativistic physics predicted in 1938 by non-dual relations for massive fields was slowed down because it was not possible for a long time to rewrite Einstein’s equation without the conceptually excessive right-hand side. During the century of speculation about the unphysical nature of the metric singularity, the flywheel of dual GR with a doubtful Schwarzschild metric gained such speed that the curved space was presented by mathematicians as a calling card of Einstein gravitation.

Doubts about the inadmissibility of singularity in field theory were ignored with reference to the already accepted energy divergence in Maxwell’s theory. There, the energy divergence of the self-action of a point source was learned to be “swept under the carpet” even in problems of quantum electrodynamics. The author of GR began to be called the “reluctant father of black holes”. Thus, for many decades it has been the case that in electrodynamics the charge moves in Euclidean space with strict conservation of the Gaussian flux through any enclosing surface, and the accompanying mass of the same carrier (electron) moves in the non-Euclidean space of GR. Here the conservation of the Gaussian flux from a point source through any closed surface is not achieved.

While time dilation has been successfully demonstrated by accurate clocks in many relativistic tests, beginning with Gravity Probe A, the curvature of the space ruler has no direct evidence. Nevertheless, the relativistic corrections to Newton’s gravity in a weakly measurable field are very successfully interpreted via the Schwarzschild metric, which Einstein did not dispute. Again, the same corrections to the weak field have been successfully calculated by the monistic theory without singularity for Euclidean matterspace [24]. So far, the accuracy of astronomical tests in the weak field is simply not sufficient to falsify either the Schwarzschild metric [12] or the alternative strong field metric [9] without deviating from the Euclidean space section in the curved 4D geometry of spacetime. Without a demonstrable falsification of the predictions of dual GR in strong fields, the Newtonian referents of empty space and massive point will not relinquish their positions in textbooks on gravitation for a long time to come. The proponents of the singularity and the metric horizon in the centre of the Galaxy have resorted to the confusing presentation of “photos” of black holes. This is despite the fact that, according to the logic of scientific discovery [27], no experiment, observation or photograph can, in principle, select the correct theory from among competing theories within the accuracy of the measurements.

The macroscopic quantisation of the magnetic flux in the superconductor ring would be destroyed by the Earth’s gravitational field if the geometry of the current loops deviated from the Euclidean one. Finally, measurements of magnetic moment variations are made with record quantum accuracy by the SQUIDs, for which metric deviations in the order of 10-9 in the Earth’s field would not go unnoticed if they actually changed the length of the quantisation contours [28]. In the experiment, there are neither variations of the quantized flux in inhomogeneous gravitational potentials, nor superconducting accelerometers due to violations of Euclidean space in accelerated systems, as expected in the dualistic GR. These inconvenient laboratory facts are ignored by the black hole community, as is Einstein’s thought experiment [14].

At one time, many 20th century theorists were opposed to the curved space in Einstein’s equation. First, Marcel Grossmann, Einstein’s co-author on the temporal modification of the Minkowski interval in 1913, refused to sign further elaborations with the curved space subinterval in the spacetime metric. Then Gustav Mee began to criticise Einstein because of the corresponding incompleteness of GR. Arnold Sommerfeld constructed self-consistent strong field electrodynamics in flat space and urged Einstein to revise his theory critically to avoid spatial curvature. The mass of a test particle cannot really move in curved space, while its associated electric charge moves in flat space.

Again Richard Feynman decided to register for a gravitational conference under a pseudonym. And in 1958, another Nobel laureate in physics, Julian Schwinger, published an article with a defiant title for relativists: “On the Euclidean Structure of Relativistic Field Theory”. In Russia, Academician V.E. Fok did not belong to the ether school of Russian cosmists, but neither did he take the reality of black holes seriously. He did not even mention them in his textbook on gravitation. Academician A.A. Logunov criticised GR immensely for allegedly inhomogeneous curvature of space and pointed to the strict conservation of 3-momentum in all known experiments. He and his co-authors tried to construct the relativistic theory of gravity exclusively with flat space, adhering to the dualistic division of matter into particles and field according to the model scenario of Maxwell’s electrodynamics with point charges.

Recall that Einstein not only criticised the Schwarzschild solution for the metric, but also searched for a way to discard the righthand part of his field equation for the transition to the non-dual physics of extended mass.But the scalar convolution of Einstein’s field tensor in the remaining left-hand side of the equation with the metric tensor again leads to the cancellation of the Ricci scalar. And there is simply no other scalar density to describe the invariant field mass in pseudo-Riemannian geometry. If the Ricci scalar density does not describe the scalar density of mass, the relativistic mechanics of massive fields could never be geometrized according to Riemann and Ricci. Recently, the monistic version of Einstein’s equation for static distributions of extended mass with equal active μ_a and passive μ_p densities has been published [9] to explain the measurable relativistic phenomena [24] in the Euclidean matterspace of Russian cosmists.

The Euclidean 3-section in pseudo-Riemannian spacetime maintains six symmetry bonds: 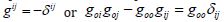. Such inhearent symmetries in the 4-geometry hold the Euclidean space of continuous mass for any elastic changes of its correlated densities under the fixed integral of motion, m = const. The geometric self-organisation of continuous material space allows 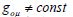for the adaptive dilation of physical time 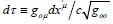in the observed effects of GR. And this time dilation in the nonlocal hierarchy is related to the metric four-potential 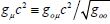of moving mass densities, not to all ten components of the metric tensor 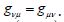By finding four components of the metric potential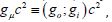

one can submit all components of the contrvariant and covariant metric tensors:

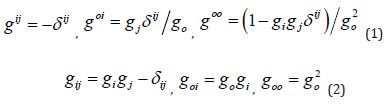
The Ricci scalar in the monistic field theory with Euclidean space describes the sum of equal active and passive mass densities, 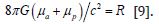The invariant divergence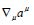of local 4-accelerations, 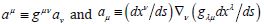, in metric spacetime for elastic material 3-densities is also the scalar density, which is proportional to the Ricci scalar 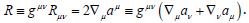Therefore, the Euclidean matterspace of Russian Cosmism relates the origine of invariant mass densities and corresponding metric fields with relativistic self-accelerations of spacetime with geometric connections. The relativistic action in this monistic theory, 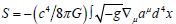, results in the symmetric stress-energy tensor for massive fields 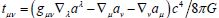and the Lagrange equation of motion:

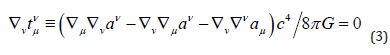
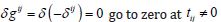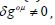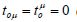The Hilbert variations of the action on the spatial components of the metric tensor because of the Euclidean space in the geometric relations (1). Variations of the action on the remaining 4 components, lead to the 4-component analogue of Einstein’s equations in monistic physics. The detailing of this tensor equation for mixed components,

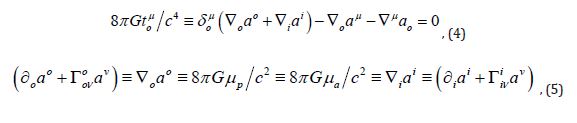
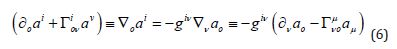
allows a self-sufficient search for metric solutions of the theory and for dynamical densities of masses without Newtonian gravitational referents. For a static equilibrium with spherical symmetry of the field densities, the system of equations (1) - (6) leads to the known [9] distribution of the extended mass 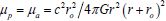with metric potentials 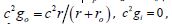and the metric 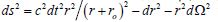with Euclidean 3-section. Again, the inhomogeneous material space with locally dilated time in this alternative metrics has successfully explained [24] the main gravitational tests of relativistic physics without departing from the 3D flatness.

The basis of communication is information. It is usually associated with the structural reorganisation of masses or their entropy after external energetic influences, including the absorption of electromagnetic waves. In the dualistic theory, masses are separated by empty space, which cannot contain information. In the monistic distribution of extended mass, space is continuously filled with information for both static states and non-equilibrium distributions. The Shannon law for the distribution of information without losses in the noise line defines optimal configurations for the field mass. In equilibrium self-distributions, the negative energy of self-interaction (−mc² ) completely compensates the internal relativistic energy mc² of the elastic Lomonosov-Umov ether [8].

In the monistic physics of field masses there is not only information transfer from one nonlocal hierarchy to another by inelastic wave processes with delay, but also information communication within elastic distributions. Each nonlocal hierarchy represents a hologram of standing ether waves with autocoherent change of averaged densities in motion. The relativistic energy of these elastic ether waves, or de Broigle waves, forms for visible bodies a kinematically variable mass-energy of Umov, 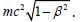The latter can be slightly disturbed by inelastic losses according to the laws of Newtonian mechanics. Therefore, the solar system maintains elastic stability of autocorrelated states for billions of years - its Lomonosov stresses “from here to there” are instantaneous and correspond to Laplace’s estimates [29]. The elastic organization of nonlocal gravity does not obey the classical mechanics of dissipative changes with temporal delays.

In the nonlocal hierarchy of the field mass, communication is instantaneous, i.e. it takes place outside world time for inelastic exchanges. The fact that instantaneous communication is part of the physical picture of the macrocosm was clearly demonstrated to physicists first by laboratory superconductors, then by nonlocal experiments with entangled photon states (Nobel Prize in Physics 2022). More recently, megaparsec coherence of matter has been established for the correlated polarisations of quasars [30] and even for the axes of galaxies in their clusters [31].

Experimental instantaneous communication in space was first confirmed by the astrophysicist N.A. Kozyrev, who in 1976 published the detection by a telescope system of signals from a distant star in three directions [32]. The first signal was from a delayed wave, as in dualistic physics. The second signal appeared when the telescope axis was aligned with the actual position of the star’s centre, i.e. instantaneously. The third signal is conventionally called the “advanced” signal. It is, however, an echo wave of disturbances in the inhomogeneous medium which returns through the telescope axis to the future position of the star centre of spherical material densities. In the physics of empty space, a returning wave cannot exist at all. Therefore, Kozyrev’s experiments, confirmed by the group of the academician Lavrentiev [33], directly falsified the world order according to Newton and supported the monistic universe with elastic material cosmos.

Non-dual physics (1)-(6) allows, in addition to dual simplifications of reality, testable predictions of nonlocal space communication, in particular for the midterm forecast of the solar activity based on data of the Baikal Deep-Sea Experiment [34]. It is to be hoped that further development of the noise immunity theory of Kotelnikov and Shannon communication in noise lines [35] will lead to useful solutions of many nonlocal problems in the field of macrophysics of misunderstood Russian cosmists.

In 1915 Hilbert very wisely proposed [25] to physicists to unite Einstein’s relativistic ideas with Gustav Mee’s field theory of matter [36,37]. From the very beginning it would lead GR on a non-dual path of describing inertial distributions of mass-energy in non-empty space. It was a collective mistake of the scientific community that Hilbert’s programme to unify the laws of physics on the monistic basis of field-mass and field-charge at the beginning of the 20th century never got off the ground. It is necessary to re-examine the reasons for the systematic defeat of the Cartesians in the natural sciences. Until then, one can only conclude that the blind faith of scientists in the ontological infallibility of Newton’s dual mechanics was too great until the advent of quantum mechanics with wave distributions of non-local organized matter. Einstein ended up transporting relativity across the ocean on the basis of Newton’s material points. And the field matter of Descartes, Mie and the Russian cosmists remained in Europe, though unused for a while.

Einstein’s physical intuition did not fail him: since 1920 he openly proposed to return the material ether to the GR [38], and since 1929 he began to call the space filled with ether a finite physical reality. In the dualistic physics of fields around a line of cylindrical sources, Einstein, together with his young co-author N. Rosen, doubted the possibility of reconciling a metric wave with a coordinate singularity on the material axis. This 1936 manuscript was rejected, as is known, by the Physical Review and lost. But in 1939, Einstein gave an exhaustive reply to all his opponents and, in the author’s opinion, quite reasonably rejected metric singularities from physical reality [14]. The Shwarzschild metric with curved space can approximate many relativistic corrections in NASA’s weak-field measurements, including those from the LLR and GPB experiments. But the same small corrections to Newtonian gravity can be provided by the monistic theory of Euclidean matterspace with adaptively delayed time [24]. Proper probes with the gravity- assist manoeuvres of satellites should quantitatively falsify the unphpysical model of curved space, if required.

The ubiquitous observation of dissipative redistributions of thermal energy, without which there would be no evolution of matter and no division of living cells, distracts scientists from the dominant tendency of nonlocal matter to reduce Shannon entropy. Elastic self-organisation of densities is permanent for any extended hierarchy under insignificant external perturbations. This is illustrated by Huygens’s example of a mechanical system of metronomes on a common table, where chaotic oscillations begin to synchronise at measurable times and inexorably reduce entropy, contrary to the hypothesis of thermal death. The phenomenon of gravitation and its modern theories confirm the universal aspiration of inertial matter to nonlocal order with geometric connections. The universal tendency to restore nonlocal order removes the problem of the irreversible growth of the entropy of the universe according to Newton’s dissipative mechanics.

Elastic self-organisation of an equilibrium system requires a stationary embedding of information in the whole space of elementary events with possibilities of local dissipation and occurrence of non-equilibrium. This means that the event space must be continuously filled with field mass, allowing the continuous distribution of information and Shannon entropy. This monistic approach, where de Broigle wave matter fills the whole universe, rejects the dualistic world view with empty space for retarded interactions.

The renaissance of Umov’s ether physics for field inertial media, whose relativistic generalisation led to the monistic analogue of Einstein’s equation (4) and to the geometrodynamic motion of massive densities according to Bianchi’s vector balances (3), may lead to philosophical changes in the concept of modern natural science. It might be necessary to change the teaching system of contemporary physics from wrong and simplified to correct and somewhat incomprehensible. Before presenting typical problems on the simplified Newtonian model, it is necessary to listen to an online introduction for schoolchildren to the nonlocal holism of matter and its model division into quasi-isolated hierarchies. A new generation of monistic physicists will explain elastic phenomena in astronomy and space communications, and master nonlocal technologies in synergetics, big data processing, biology, medicine, ecology and climate.

1. Aristotle: Metaphysics (350 B.C.E.), Books 1-14, Trans. by W. D. Ross, The Internet Classics Archive.
2. Garber D (1992) Descartes\rq {} Metaphysical Physics. University of Chicago Press, Chicago.
3. Daniel Garber (1992) Descartes Physics. The Cambridge Companion to Descartes, J Cottingham, Eds.; New York: Cambridge University Press pp. 286-334.
4. Rowland RD (2015) On claims that general relativity differs from Newtonian physics for self-gravitating dusts in the low velocity, weak eld limit. International Journal of Modern Physics D 24(08): 1550065.
5. Vernadsky VI (1988) Philosophical thoughts of a naturalist. Academy of Sciences of the USSR; Ed. coll. AL Yanshin, SR Mikulinsky, II Mochalov; co-editor. MS Bastrakova, et al. - Moscow: Nauka, 520 с. (in Russian).
6. Lomonosov MV (1743) Notes on the severity of bodies. Complete Works, 11 Vols., Vol.2, eds. S Vavilov and T Kravetz. Akad Nauk SSSR. Moscow and Leningrad (1950).
7. Umov NA (1874) Beweg-Gleich. d. Energie in contin. Korpern. Schomilch. Zeitschri d. Math. und Phys. XIX.
8. Bulyzhenkov IÉ (2025) Instantaneous correlations of Shannon's big data in nonlocal cosmos. Front Astron Space Sci 11: 1433214.
9. Bulyzhenkov IÉ (2008) Einstein's Gravitation for Machian Relativism of Nonlocal Energy-Charges. Int J Theor Phys 47(5): 1261-1269.
10. de Sitter W (1916) On Einstein's Theory of Gravitation and its Astronomical Consequences. Second Paper. Mon Not Roy Astron Soc 77(2): 155-184.
11. Shapiro II, Resenberg RD, Chandler JF, Babcock RW (1988) Measurement of the de Sitter precession of the Moon: A relativistic three-body effect. Phys Rev Lett 61(23): 2643-2646.
12. Schwarzschild K (1916) On the Gravitational Field of a Mass Point according to Einstein’s Theory. Sitzungsber Deut Akad Wiss, Berlin pp. 189-196.
13. Williams JG, Newhall XX, and Dickey JO (1996) Relativity parameters determined from lunar laser ranging. Phys Rev D 53(12): 6730-6739.
14. Einstein A (1939) On a Stationary System with Spherical Symmetry Consisting of Many Gravitating Masses. Ann Math 40: 922-936.
15. Narlikar JV, Dadhich N, Krishna Rao J, Vishveshwara CV (1985) A Random Walk in General Relativity and Cosmology, ed. by NK Dadhich, J Krishna Rao and CV Vishveshwara (Wiley Eastern, New Delhi) p. 171.
16. Narlikar JV, Padmanabhan T (1988) The Schwarzschild solution: Some conceptual difficulties. Foundation of Physics 18(6): 659-668.
17. Brillouin L (1970) Relativity reexamined. New York: Academic Press.
18. Everitt CWF, DB DeBra, BW Parkinson, JP Turneaure, JW Conklin, et al. (2011) Gravity Probe B: Final Results of a Space Experiment to Test General Relativity. Phys Rev Lett 106(22): 221101.
19. Everitt CWF, B Muhlfelder, DB DeBra, BW Parkinson, JP Turneaure, et al. (2015) The Gravity Probe B test of general relativity. Class Quantum Grav 32: 224001.
20. Schiff LI (1960) On Experimental Tests of the General Theory of Relativity. American Journal of Physics 28(4): 340.
21. Einstein A, Infeld L, Hoffmann B (1938) The gravitational equations and the problem of motion. 39(1): 65-100.
22. Landau LD, Lifshitz EM (1975) The Classical Theory of Fields. Pergamon, Oxford, para 106, prob 4.
23. Einstein A, Grossmann M (1913) Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation. Zeits Math und Physik 62: 225-261.
24. Bulyzhenkov IÉ (2012) Geometrization of Radial Particles in Non-Empty Space Complies with Tests of General Relativity. Journal of Modern Physics 3(10): 1465-1478.
25. Hilbert D (1915) Die Grundlagen der Physik, Nachrichten K. Gesellschaft Wiss. Gottingen, Math-Phys. Klasse, Heft 3: 395-407, eq. 22.
26. Einstein A (1915) Die Feldgleichungen der Gravitation. Sitzung der Physikalisch-Mathematischen Klasse 25: 844-847.
27. Popper K (1934) Logik der Forschung, Vienna
28. Bulyzhenkov IÉ (2009) Relativistic quantization of Cooper pairs and non local electrons in rotating superconductors. Jour Supercond Nov Magn 22(7): 627-629.
29. Laplace PS (1795) Le Systeme du Monde. Paris.
30. Hutsemékers D, Braibant L, Pelgrims V, Sluse D (2014) Alignment of quasar polarizations with large-scale structures. Astron Astrophys 572: A18.
31. Lee JH, Pak M, Song H, Lee H-R, Kim S, et al. (2019) Mysterious coherence in several-megaparsec scales between galaxy rotation and neighbor motion. Astrophys J 884(2): 104.
32. Kozyrev N (1976) Flare Stars. Proceedings of the Byurakan Symposium, October 5-8, (AN ArmSSR Yerevan, 1977, published in Russian), 209-227.
33. Lavrent'ev MM, Eganova IA, Medvedev VG, VK Oleinik, SF Fominykh (1992) Scanning of the stellar sky by the Kozyrev dedector. Dokl A N 323(4): 649-652 (in Russian).
34. Korotaev S, Budnev N, Serdyuk V, Kiktenko E, Orekhova D, et al. (2022) Macroscopic nonlocal correlations by new data of the Baikal Experiment. J Phys Conf Ser 2197: 012019.
35. Unser M (2000) Sampling - 50 years after Shannon. Proc IEEE 88(4): 569-587.
36. Mie G (1912) Grundlagen einer theorie der materie. Ann der Physik 37: 511-534.
37. Mie G (1912) Grundlagen einer theorie der materie. Ann der Physik 39: 1-40.
38. Einstein A (1920) Ether and the Theory of Relativity. Lecture at the University of Leiden on 5 May (published in English by Methuen & Co. Ltd, Lon don,1922).