Gravity in Space

As is known, the founder of the theory of universal gravitation, I. Newton [1], indicated material bodies as the source of forces of attraction. In 1915, 1916 And Einstein proposed the general theory of relativity [2]. In this theory, gravitational effects are caused not by the force interaction of bodies and fields, but by the deformation of space-time itself. Deformation is associated with the presence of mass-energy.

These theories have one common condition-the forces of attraction are created by the masses of bodies. Based on this condition, the conclusion follows-the forces of gravity act centrally symmetrically. That is, they decrease with distance from the body equally, in all directions.

In the author’s theory of vortex gravity [3], it is stated that the forces of attraction act in space flatly-symmetrically with respect to any space object.

Our Universe has unique qualities, which include the universal rotation of all celestial objects (celestial bodies or systems of bodies), of which the visible Universe consists. To date, there is no gen erally accepted scientific explanation for these rotations. The proposed model of gravity, cosmology and cosmogony is based on the condition that celestial objects received the impulse of their rotation from the vortex rotation, in the corresponding celestial region, of the cosmic, gaseous medium called the ether. The rotation of the ether is carried out in accordance with the circulation of celestial bodies around the center of rotation. That is, the orbital speeds of rotation decrease in the direction from the center of rotation to the periphery, according to Kepler’s 3rd law, provided that the orbital trajectories of the ether are circular. In accordance with the Bernoulli principle, the change in orbital velocities causes an inversely proportional change (increase) in the pressure in the ether. The pressure gradient creates buoyancy forces. The buoyant force is the gravitational force.

Since the vortex rotates in one plane, the decrease in the pressure of the ether occurs in the plane of rotation of the ether. Based on the law of Archimedes, all bodies are pushed into the plane in which the least pressure occurs. Therefore, the gravitational forces act in a plane-symmetrical manner and it is necessary to abandon the classical model of the centrally symmetrical action of the gravitational forces. Ether is an extremely low dense gas that permeates all bodies (substances), except for superdense ones. Therefore, the ether can push out only these superdense bodies. These superdense bodies include the nucleons of atoms.

In the theory of vortex gravitation, the Navier-Stokes equation for the motion of a viscous liquid (gas) was used to determine the pressure gradient in the ether vortex.

After the transformations, an equation was obtained for determining the forces of gravity in the ether vortex:

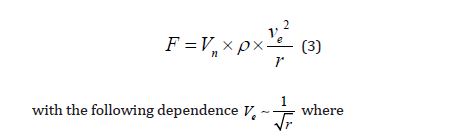
V_n -the volume of nucleons in the body, which is in the orbit of a torsion with a radius -r.

ρ = 8.85 x 10^-12 kg/m³ - ether density [4]

v_e -speed of the ether in orbit r

r -radius of considered ether vortex orbit

Let us replace in equation (3) the volume of nucleons by their mass, using the well-known dependence:

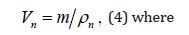
m is the mass of nucleons in the body

Substituting (4) into (3) we get

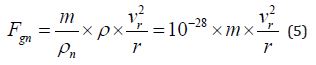
Note 1. Using the equations of vortex gravity (3) and (5), it is possible to calculate the gravitational forces that act only in the plane of the vortex (torsion). To determine the forces of attraction at any point, additional studies are presented below.

As you know, the planets revolve around the Sun in an ellipse with a slight eccentricity. This fact can be explained from the standpoint of vortex gravity. In addition, the elliptical trajectory of the planets will allow the calculation of gravitational forces in a three-dimensional model. The reason for the appearance of “compression” of the orbits of the planets is the inclination of the plane of these orbits to the plane of the solar, gravitational torsion, which is proved by the following conditions. As is known, the planes of orbital motions of all planets are located with small deviations from each other. Consequently, the planes of the orbits of the planets also have an inclination to the plane of the solar gravitational torsion, where the greatest gravitational force acts on each orbit, and they (the planets), during their orbital motion, must cross the solar torsion at two points. These points of intersection are called the centers of perihelion and aphelion.

At aphelion and perihelion, the force of solar gravity acts on the planets with the greatest magnitude in this orbit and, therefore, the planet’s orbit has the maximum curvature. When the planet exits (deviates) from the plane of the solar torsion, the forces of gravity decrease, and the trajectory of the planets “straightens out”. A similar cycle of changes in gravitational forces and the trajectory of movement is repeated for each planet in each revolution around the Sun. The more the planet’s orbital trajectory deviates from the central plane of the solar torsion, the more the gravitational forces decrease in these areas. Therefore, the orbit must “shrink” more. The constant, cyclic change of these forces gives the circulation trajectory an elliptical shape.

At significant inclinations and high speeds, the orbit of a satellite (meteorite, comet) acquires a hyperbolic or parabolic trajectory. Therefore, a celestial body, having once circumnavigated the Sun, leaves the gravitational field of the solar torsion forever.

The change in the dynamic properties of the planets when they turn at points with inclinations to the plane of the gravitational torsion, indicated in Ch. 3 provides an opportunity to obtain a formula that describes the change in gravitational forces in a three-dimensional model.

Comparing the coefficients of compression of the orbits of all planets with the cosine of the angle of inclination of these orbits to the plane of the solar torsion, we determine that these quantities have a directly proportional relationship:

b/a ~ Cos β (6)

(Figure 1)

The X axis is the projection of the central plane of the torsion bar.

axis Z -axis of rotation of the torsion bar

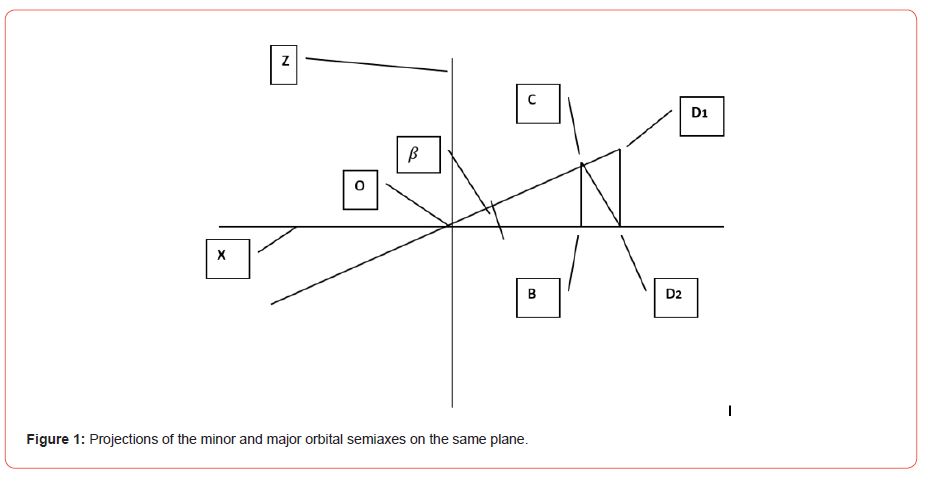
β is the angle of inclination of the orbital plane of the planet to the plane of the gravitational torsion.

a is the projection of the major semiaxis of the ellipse,

c -projection of the minor semiaxis

OB is the radius of curvature of rotation of the torsion-satellite at perihelion or aphelion, or at the top of the semi-major axis of the orbit:

ОВ = b² / а (7)

OD₁ is the radius of curvature of the torsion-satellite at a point having an inclination by an angle β from the central plane of the parent torsion. That is, at the top of the minor semiaxis of the orbit.

OD₁ = а²/ b (8)

Let us prove that equation (6) is satisfied under equalities (7) and (8)

Proof:

Let us plot on the X axis (Figure 1), which coincides with the line of apsides, a segment OB equal to the radius of curvature at the apex of the major semiaxis, the direction of which coincides with the central plane of the solar torsion.

Let’s draw a line from the center O at an angle β, in the direction from the minor semiaxis.

Since, according to the condition cos β = b/a = OB/OC, it follows from here:

OC = OB a/b = (b²/a) (a/b) = b

Let’s draw a perpendicular from point C to the X axis, since the angle OCD2 is a straight line, then:

OC/OD₂ = cos β = b/а, whence

OD₂ = OC а/b = b (a/b) = a,

Let’s draw a perpendicular from point D2 to the OS, since the angle D₁ D₂ O is a straight line, then:

OD₂ / OD₁ = cos β = b/a, whence OD₁ = OD₂ (a/b) = (a²/b)

Let’s draw a perpendicular from point D2 to the OS, since the angle D₁ D₂ O is a straight line, then:

OD₂ / OD₁ = cos β = b/a, where OD ₁ = OD ₂ (a/b) = (a²/b)

Therefore, equations (7) and (8) are satisfied under the condition cos β = b/a. That is, the cosine of the angle of inclination of the planet’s orbital plane at the vertex of the minor semiaxis to the solar torsion plane is equal to the compression ratio of this orbit.

Note 2. The inclination β of any orbital point does not coincide with the inclination angle i of this point, indicated in astronomical calendars, since according to astronomical rules, all coordinates in the solar system are measured heliocentrically and relative to the ecliptic plane.

Let’s write the formulas for determining the radius of curvature of the orbit (ellipse):

- at the apex of the semi-major axis or at perihelion and aphelion:

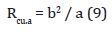
- at the top of the minor semiaxis

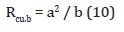
Based on Kepler’s 2nd law, within their orbit, the planets change their orbital velocity (V) depending on the distance from the Sun (R) in the following proportion:

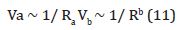
V_a - orbital velocity at perihelion (or aphelion), that is, at the top of the semi-major axis of the planets’ orbit,

V_b - orbital velocity at the vertex of the minor semiaxis of the planets’ orbit

R_a is the distance from the Sun to the center of aphelion (perihelion).

R_b is the distance from the Sun to the top of the minor semiaxis.

R_cu is the radius of curvature of the orbit

Centrifugal forces are determined by the formula:

Fc = m V² / R_cu (12)

Substituting (9) - (11) into (12) we get:

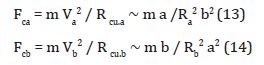
Since the gravitational forces at aphelion or at perihelion Fg correspond to their classical values or centrifugal forces, then to determine the deviation of the gravitational forces on the periphery of the torsion (at the apex of the semi-minor axis - point b), it is necessary to determine a similar deviation of the values of centrifugal forces compared to the same forces at perihelion. To do this, we divide formula (14) by formula (13):

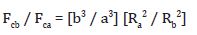
Here, the relative value R_a²/ R_b² ,in accordance with formula (5) or Newton’s formula, determines the change in the magnitude of gravitational forces, depending on the change in the distance from the center of the torsion to the points under consideration.

According to formula 6 of this chapter, the value of b/a is equal to the cosine of the angle of inclination of the considered point. Consequently, this value determines the change in gravitational forces depending on the inclination of the considered point to the plane of the solar torsion.

Then you can write:

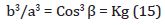
The forces of gravity at any point of any comic space are determined by the formula:

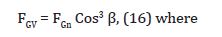
F_gn -gravitational force in a two-dimensional model (f. (5) or Newton’s equation)

F_gv is the gravitational force in the 3D vortex model.

Therefore, with the help of the gravitational coefficient Kg, one can determine the gravitational forces at any point of any space torsion far from the center.

Note 3. In the central peripheral part of the torsion, due to the end vortices of the ether, formula (16) cannot describe the distribution of vortex gravity forces.

Formula (16) shows that when moving away from the plane of the gravitational torsion in the direction parallel to the axis of the torsion, the gravitational force decreases in inverse proportion to the cube of the distance of this removal - 1/s³.

In the author’s article [3], the calculation of the gravitational forces acting on the planets Mercury and Pluto during their location in orbit at the top of the minor semiaxes was made. At these points, the orbits of the planet deviate to the maximum from the plane of the solar gravitational torsion. The calculation was made on the basis of Newton’s equation of universal gravitation and the equation of vortex gravity (equation 5). The results obtained were compared with the centrifugal forces at these points.

Note 4. Centrifugal forces can be calculated as accurately as possible and are always equal to gravitational forces. Therefore, centrifugal forces can be used as a standard for the accuracy of results in determining gravitational forces.

Distances and speeds of celestial bodies are taken on the basis of the astronomical calendar [5]

1. . Pluto

The length of the semi-major axis of Pluto’s orbit a = 5906.375 x 10⁶ km

The length of the minor semiaxis b = 5720.32 x10⁶ km

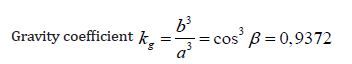
Distance from the Sun to the top of the semi-minor axis of Pluto’s orbit d = 5907.963 x 10⁶ km

Radius of curvature at the top of the minor semiaxis R_b = a² / b = 6098.48 x 10⁶ km

Pluto’s orbital velocity at the apex of the minor semiaxis V_b = 4.581km/s

Centrifugal forces at the top of the minor semiaxis based on the above characteristics:

Fc = 0.00344 Mp, where Mp is the mass of Pluto

The forces of solar gravity at the same point (according to the classical Newton model)

Fgn = 0.00382 MP (difference with centrifugal forces + 11.1%)

Forces of vortex gravitation taking into account the gravitational coefficient (equation 7)

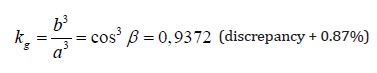
2. Mercury

The length of the semi-major axis of the orbit of Mercury a = 57.91x 106 km

The length of the minor semiaxis в = 56,67х106 km

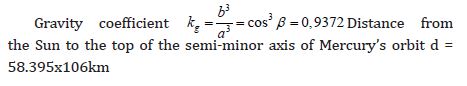
Radius of curvature at the top of the minor semiaxis Rb = a² / b = 59.177x10⁶ km

Orbital velocity of Mercury at the top of the semi-minor axis V_b = 46.4775 km/s

centrifugal forces

Fc = 36.503 Mm , where Mm is the mass of Mercury

Gravitational forces:

According to Newton Fgn = 39.09 Mm, (difference +7.1%)

According to the theory of vortex gravity Fgv = 39.09 x 0.9372 x Mm = 36.63 Mm (difference + 0.35%)

It is obvious that the calculation according to the theory of vortex gravity is an order of magnitude more accurate than the classical method and in its accuracy corresponds to the accuracy of astronomical measurements.

In addition, on the basis of equation (7) it is obvious that for large deviations of the considered point from the gravitational plane, the calculation of gravitational forces according to the classical equation will lead to an absurd result.

Based on the above calculations, it can be argued that the true cause of gravity is a decrease in pressure in the ether, which is caused by the vortex rotation of this ether. Accordingly, the gravitational- barial field, into which all substances are drawn, has the shape of a disk.

Probably, Huygens was right about the assessment of Newton’s hypothesis about the gravitational properties of bodies, which created and creates many problems in the scientific world. The author outlined these problems in his article “Paradoxes of the Theory of Gravity”[6].

The theory of vortex gravity provides researchers with great scientific opportunities for new consideration of various physical properties and phenomena that have controversial explanations. Based on the theory of vortex gravity, the author proposed and published his physical models for the following phenomena:

-Origin and properties of Black Holes [7]

-Gravitational properties of atoms [8]

-The genesis of the planet Earth [9]

-Equivalence of energy and atomic gravity [10]

-Invariance of the speed of light [11]

-Masses of celestial bodies [12]

-Photon mass [13]

-Reasons for the removal of the moon [14]

-Why did the global glaciation occur [15]

-Causes of high and low tides [16]

-The optimal trajectory of space flights [17]

None.

No conflict of interest.

1. Newton, Sir Isaac (1729) The Mathematical Principles of Natural Philosophy, Volume II.
2. Albert Einstein «Die Feldgleichungen der Gravitation». Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin: 844-847.
3. S Orlov. Foundation of vortex gravitation, cosmology and cosmogony. Global journal of science Frontier V 
4. V A  Atsurovskiy (1990)  General ether-dynamics. Energoatomizdat. Moscow,  Russia, Page 278.
5. A P  Gulyaev (1993) Astronomy calendar. Moscow, Russia, Page 285.
6. (2014) Paradoxes of the Theory of Gravity. International Journal of Astrophysics and Space Science 2014; 2(1): 6-11.
7. International Journal of Astronautics and Aeronautical Engineering (ISSN: 2631-5009) Volume 2, Issue 1 Review Article.
8. Journal of Physics and Astronomy.
9. Physics & Astronomy International Journal.
10. International Journal of Robotics and Automation.
11. Natural Products Chemistry & Research.
12. International Journal of Advanced Research in Physical Science (IJARPS) Volume 6, Issue 2, 2019, PP 24-29.
13. Orlov (2018) J Aerosp Eng Mech 2(1):152-155
14. Scientific Journal of Pure and Applied Sciences.
15. Journal of Physics Research & Reports.
16. American Journal of Engineering Research and Reviews.
17. American Journal of Aerospace Engineering.