Study on Vibration of Directional Drill String with Affecting the Important Parameters with Energy Considering

The vibration of drill string system may reduce the life of the used pipes and tools by accelerating the process of crack propagation and fatigue. Furthermore, undesired vibration can cause pipes and tools failure, wash-outs and diminish in the infiltration rate practically. In applied and engineering sciences, the vibration is one of the most important factors in designing, operation and lifetime of the drill strings. So, study on nonlinear vibrations in drill string such as every other rotary machine is essential and vital. The drill string costs may be diminished using recent technologies which make the drilling process more professional and beneficial. Drill string vibrations are usually intricate because all axial, lateral and torsional vibrations are present and coupled linearly and nonlinearly [1,2]. For instance, stick-slip torsional motion cause high bit speed level which excite severe axial and lateral vibrations [3]. To solve this, one can increase rotary table speed beyond a threshold value, because stick-slip vibrations are self-excited, but this solution may lead to lateral problems [4]. These vibrations happen simultaneously and lead to early fatigue of tools, reduction of bit life, reduction of rate of penetration and abrasive wear of tubular, which make oil well drilling inefficient and costly. Furthermore, impacts with the borehole wall can form the over gauge hole or make problem with directional drilling [3,5]. Analyzing drill string’s vibrations would help to have a design criterion for parameters in which drilling is stable and safe. Jansen [5,6] studied the transverse vibrations of drillstring caused by whirling considering contacts with the wellbore wall. Yigit and Christoforou [4,7,8] worked on dynamic models of nonrotating and rotating drill string. They studied coupled vibrations between axial-transverse and torsional-transverse using Lagrangian formulation and the assumed modes method discretely. Some studies have been done on dynamic analysis of drill strings using FEM [9,10] and experimental method [11]. Many researches were performed about bending vibration and stability [12,13], modeling of mud [14] and modeling of rotating beam and its dynamics and other important researches [15-17], and vibrations in various systems [18] and complex variable method CVM [19]. Experimental and numerical investigation has been studied and analyzed to evaluate the effective geometrical parameters of the core on the overall sound level of transformers (nonlinear vibration) [18].

The original aim of this research work to introduce and analyze the nonlinear model and study on time response for a drill string system dynamic in an inclined well assuming mud flow rate by finite element method and energy considering. In the present paper the nonlinear formulation of the directional drilling dynamics is presented and analyzed with effects of the mud flow rate, WOB and angular velocity on the drill string stability and time response simultaneously.

Here, the general model of a drill string is introduced schematically (Figure 1). In which, each part of it like pipe or collar is supposed to be empty solid cylinder with identical cross section. The rotation speed is assumed to be constant. Also, gyroscopic moments owing to rotation of the drill string and transverse vibration are included through external virtual work terms generally. Drill string vibrations may be divided into three types, or modes: axial, torsional, and lateral (Figure 2). The destructive nature of each type of vibration is different [16,20].

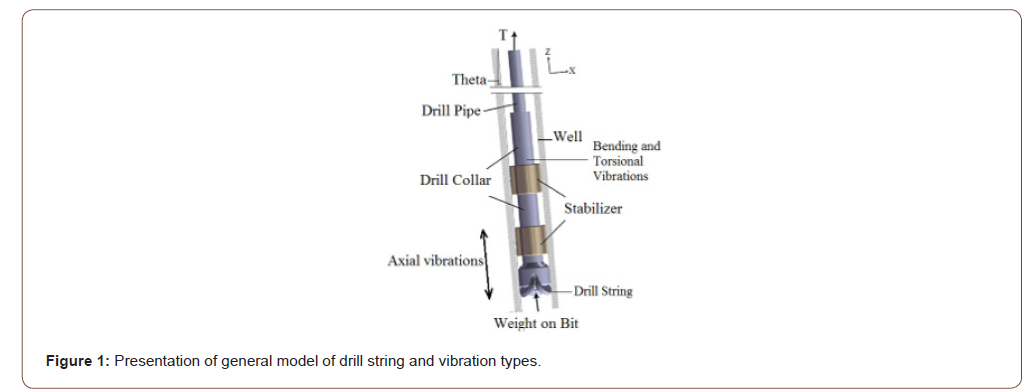
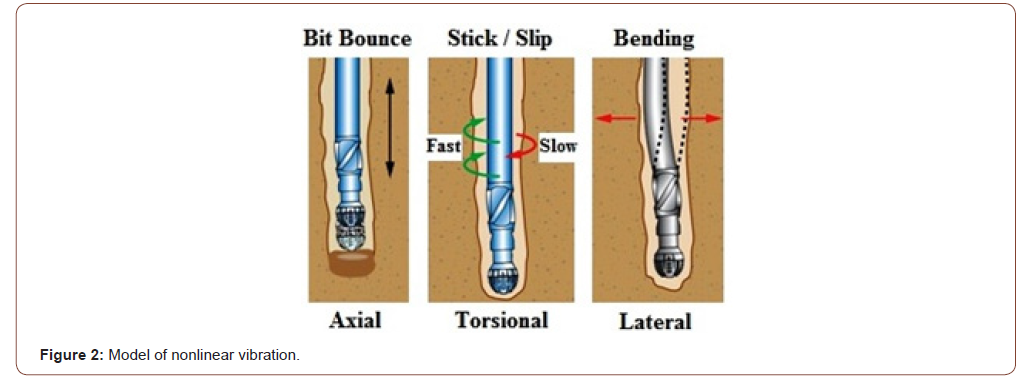
The effect of drilling mud as an important factor on stability and vibration of drill string is less considered in the literature [16,20]. Weight on bit, drilling mud flow rate and angular velocity of rotating drill string are the most important factors in stability of drilling which are considered simultaneously in the present study. In this paper the eccentricity of drill string is omitted and the system is assumed to be balanced with neglecting the helical buckling.

In the state of the equilibrium, the displacement rate field makes the total potential energy stationary with respect to virtual displacements statically. It can further be shown that for the equilibrium to be stable, the total potential energy must be a minimum. If is a local minimum, so, for any nonzero virtual displacement rate field , must be positive. In addition, kinetic and potential energies of a rotating beam element with constant angular velocity are introduced as the following,

Where δWF, δWgs are the virtual works due to drilling mud forces and gyroscopic moments respectively. Whenever the axis about which a body is spinning is rotating about another axis gyroscopic moments occur.

After finalizing equations of motion and stability analyses, using some illustrative examples, formulations will be checked. Assuming no deviation angle (Theta=0), no rotational speed (ω=0), uniform cross section of the drill string, and also neglecting the effects of drilling mud (ρm=0) it can be modeled by a standing column with pin boundary conditions affecting by its own weight aside of axial outer force which is studied by Timoshenko. The values of a, b for a simply supported column are tabulated for theoretical and both linear and nonlinear finite element method with numbers of elements in Table 1. Note that index TH refers to theoretical results calculated by Timoshenko and FE refers to finite element results.

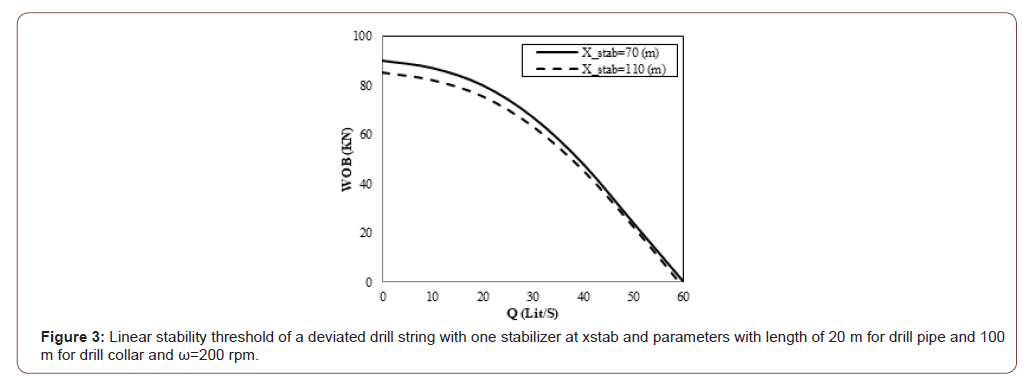
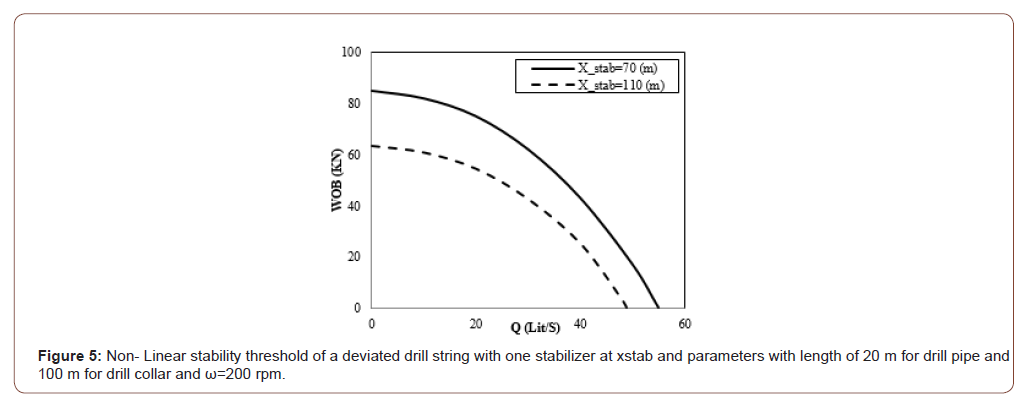
Reviewing results of Table 1 would show that linear finite element method does match theoretical results with a very good precision by very low number of elements. But nonlinear results show more error. Instability in drilling is usually caused by weight on bit and mud flow rate. Figures 3 & 5 show the behavior of “WOB” for different “Q’s” that calculated in this article and determined theoretically. In Figure 5 stability threshold of drill string using linear and nonlinear theories in deviated wells are presented. In these figures the effect of the position of the stabilizer on stability threshold is demonstrated. In all figures, height of the neutral point which causes buckling is known as the critical height of neutral point and represented by (H). WOB force can be written as,

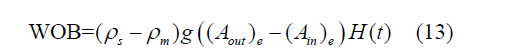
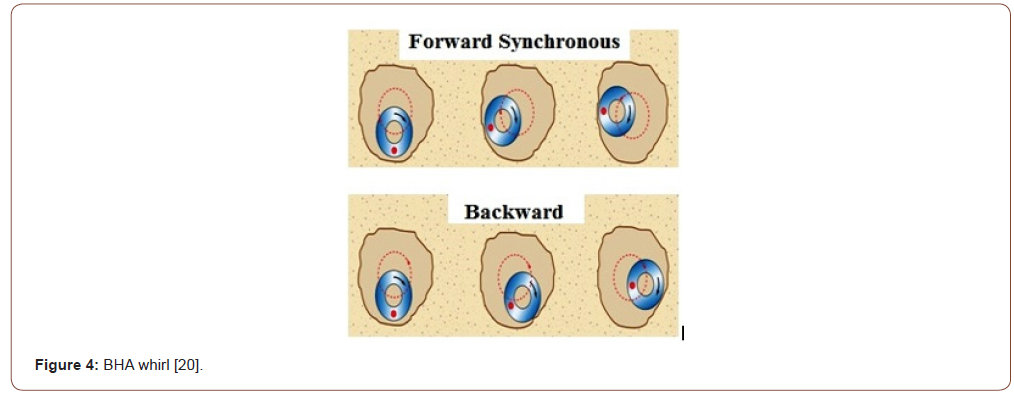
Lateral vibrations are the most destructive type of vibration and can create large shocks as the BHA impacts the wellbore wall. The interaction between BHA and drill string contact points may, in certain circumstances, drive the system into backward whirl. Backward whirl is the most severe form of vibration, creating high-frequency large-magnitude bending moment fluctuations that result in high rates of component and connection fatigue. Imbalance in an assembly will cause centrifugally induced bowing of the drill string, which may produce forward whirl and result in one-sided wear of components (Figure 4) [20]. In these figures (Figures 3 & 5) each curve represents the stability criteria under which presents the safe design parameters. These figures indicate nonlinear terms play an important role in the stability threshold and cannot be neglected. Different positions of the stabilizer allow the designer to study the effect of the parameters on stability criteria. Stability threshold of criteria in limit will be the same as Paidoussis formulations. Time response and stability of the drill string is assumed employing FEM and effects of the drilling mud flow rate is investigated which acts like a damper. Because of deviation angle, weight of drill string causes deflection in the drill string which rotates and makes whirling in vibration. The obtained outcomes and results prove that the changes in weight on bit, mud flow rate, angular velocity and deviation angle are very vital because they affect on stability of the drill string.

Table 1:Comparison of critical compression axial load factor b by two theoretical and finite element method for same dimensions and weight (same a factor).

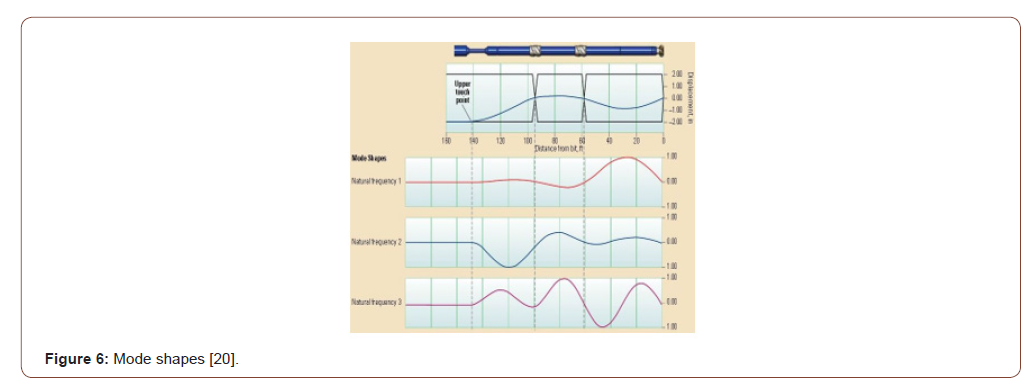
Natural frequencies are frequencies at which a structure likes to move and vibrate. Each natural frequency has an associated mode shape (Figure 6). If the structure is excited at one of its natural frequencies, then resonance is encountered, and large amplitude oscillations may result. The largest amplitude displacements tend to occur at the first (fundamental) natural frequency [20]. It is important to bear in mind that vibration models require inputs that are commonly unknown or not available in real time, including formation properties and heterogeneity, BHA component imbalance and orientation, BHA misalignment (bent collars), down hole damping, and the friction factor at contact points (transient models). Models are also sensitive to hole diameter or stabilizer clearance. For these reasons, models are most powerful when used to compare the sensitivity of different BHA options to vibrations, and their accuracy improves when calibrated using offset well information and experiences. Because of the wide range of factors that influence vibration models, the models should be viewed as guidelines and used in conjunction with real-time measurements. Vibration models are a valuable tool as part of an engineered approach incorporating prejob analysis of offset well information, prejob modeling, real-time shock and vibration measurements, and postjob analysis and modeling, but it is important to understand their limitations [20].

Effects of mud flow rate, weight on bit, angular velocity and deviation angle on instability and time response of an inclined drill string were studied. In this problem using Lagrangian technique coupled potential and kinetic energies of drill string, are written in integral forms with energy considering. Also, FEM was employed to analyzing and formulations. In addition, angular velocity, mud flow rate and weight on bit are the major parameters affecting the instability of the drill string system. So, deviation angle causes stability criteria curvature to be lower logically. That is, the system is more susceptible to drill string parameters clearly. This occurrence is more vital when the nonlinear terms are supposed and considered. Finally, diminishing the weight on bit and enhancing the mud flow rate along with the deviation angle are resulted to the lesser natural frequencies generally. Also, unwanted and undesirable vibration waves, the drilling fluid flow rate, friction, torsional vibrations and structural parameters are very important for designing the drill string systems. So, the optimal and accurate control technology is vitally required for drill string system designing and improvement of its performance.

None.

No conflict of interest.