Lattice Boltzmann Method Computation of Turbulent High-Temperature Plasma Jets

The Computational Fluid Dynamics (CFD) technique has been developed into a branch of fluid mechanics since 1960s and is mainly designed to solve the hydrodynamic equations based on the continuum assumption. Afterwards, the molecular dynamic simulation (MDS) was used to understand micro/Nano scale phenomena due to the growing interest in science and technology. The MDS is too expensive and its application has been limited to disadvantageous temporal and spatial scales. Researchers interest focused thereafter on multiscale flows. New techniques called ‘mesoscopic methods’ have met with particular attention. The so popular Lattice Boltzmann Method (LBM) is one of the emerging mesoscopic methods and had a number of distinctive features.

The LB method has received exceptional attention the last two decades. A rapid rise was noted for the application of the LBM, including physical, chemical, biological, and sciences for academic, research and engineering purpose. The number of published scientific articles marks the trend of an exponential increase. Moreover and unlike conventional methods based on a macroscopic continuum equation, the LB method starts from mesoscopic kinetic equation of the Boltzmann equation, to determine macroscopic fluid dynamics. The macroscopic fluid dynamics has emerged from the causal dynamics of a fictitious set of particles, whose motion and interactions are confined to a regular spacetime lattice. The kinetic nature brings certain advantages over conventional numerical methods, as natural for parallel computing, easy handling of complex geometries, particle-based method, only density distribution function fk (x, t) as dependent variable, algebraic operation, a large range of applicability from microscopic to macroscopic scales. The LBM has, also, the beneficial feature of simulating complex fluid flows such as multiphase flows [1], multicomponents [2] flows, porous media flows, flows with suspensions and compressible flows [3-5].

Besides, the LB thermal models have been used to simulate free fluid flows, flows and heat transfer in porous media, jet flows for laminar and turbulent regimes. The models have also been used to investigate droplet impingement and splashing on solid surface, droplet dynamics, droplets solidification, evaporation, deformation and break-up [6-9]. The temperature is varied to some hundreds of Celsius degrees (°C) where the profiles can be interpolated or linearized by hundreds of intervals.

However, our work on plasma jets and plasma spraying processes presents new issue due to the extremely high-temperatures and the non-smoothed temperature dependence of all thermo-physical gas properties near ionization and dissociation points (Figure 1).

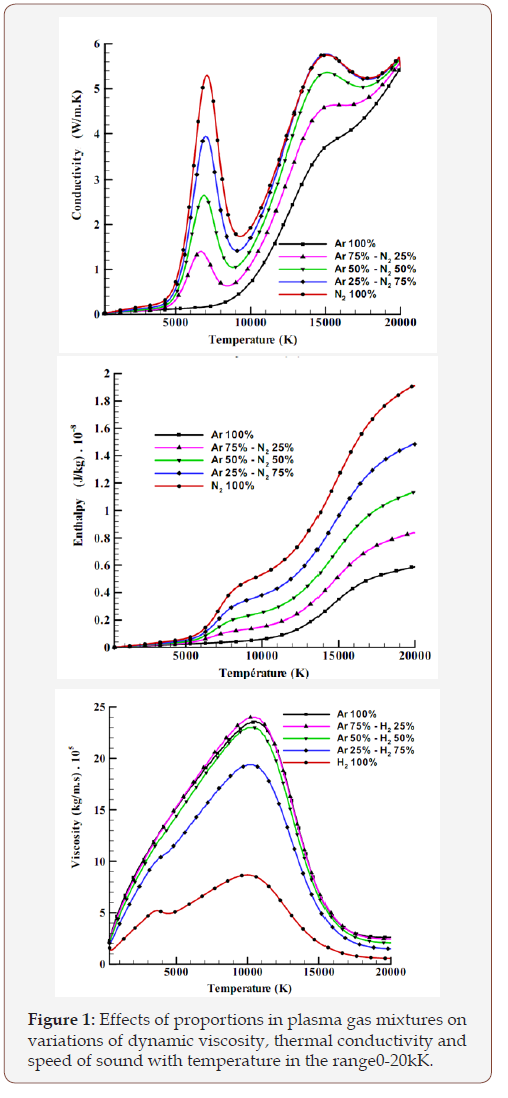
However, for the simulation of plasma jets, the temperature may reach 20kk. In this context of complexity, we have established a general framework of conversion between LB and Ph units (spaces) for the simulation of flows and transfers at extremely hightemperature with help of the Lattice Boltzmann method.

Along with the present study we will present the conversion principle to follow for the simulation of some complex problems. We will present also some results of validation for axisymmetric thermal LB model and the results of physical temperature and velocity distributions.

Some basics of the LB method

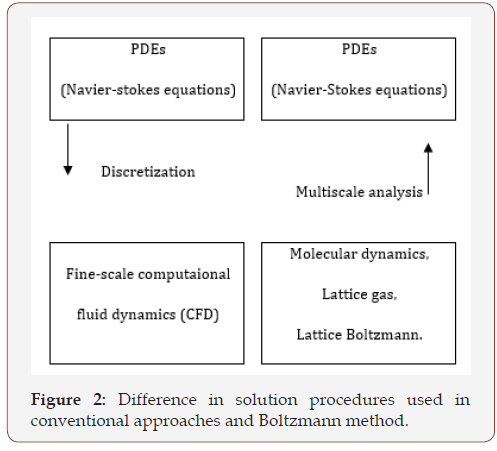
The LBM method and its ancestor LGA (lattice gas automata), in contrast to conventional approaches, are mesoscopic approaches based on the kinetic theory. The Boltzmann equation solves mesoscopic equations for the overall average of a fluid particle distribution in motion and interaction in a discreet lattice. A multiscale analysis is then performed to find or recover the macroscopic quantities. Figure 2 describes the difference between the PDEs resolution procedures used by conventional approaches and Boltzmann method.

The Boltzmann equation is derived from the statistical physics and describes the probability of existence of a particle at the time t having a velocity 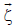in an elementary volume 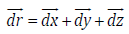and in term of distribution function

Where is an external force and Ω( f ) is an operator describing the particles interactions following the collision process. It is worth mentioning here that the time evolution of the distribution function f is, then, governed by three terms: thadvection term , the external force term 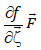and the collision term Ω( f ) .

The so-popular BGK lattice Boltzmann model assumes that the distribution function f relaxes towards the Maxwellian distribution f^eq over an average time τ_f which controls the rate toward equilibrium from the non-equilibrium state and is related to the time between two particle-collisions,

The equilibrium distribution function f ^eq was chosen to be an expansion in the velocity and to ensure that the conservation laws were obeyed.

The discretization of Equation (1) along specific directions of linkages defining the velocities lattice leads to its discrete form in terms of functions f_k as follows:

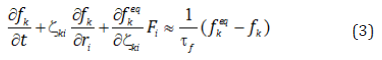
The indexes k and i describe the linkages directions and the Cartesian coordinates components, respectively. Following a time and space finite difference discretization and assuming Δx = Δt , the Boltzmann equation general form accounting for forcing term k_F , is written as:

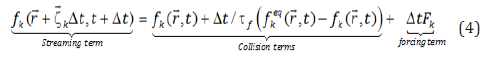
The time evolution term of Equation (4) is solved in two steps known as the collision-streaming process:

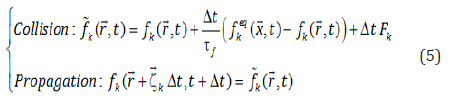
The Navier-Stokes equations are second-order nonlinear equations in velocity; therefore, the quantity 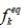should be expressed in form as an expansion 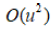of the Maxwellian distribution and is written for D2Q9 model as:

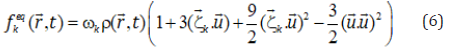
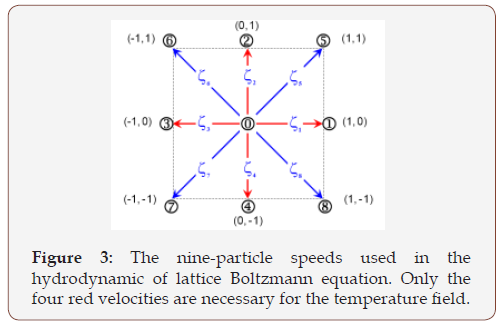
Where ω_k=4 / 9 for k=0, ω_k=1/ 9 for k=1-4, ω_k=1/ 36 for k=5-8,| 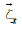|=1 along the axis and | 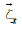|= along the diagonals (Figure 3).

Assumptions

In the present study, an axisymmetric thermal LB model for APS process has been developed based on the following assumptions for both the hot gas flow and the powder dynamics:

• The argon plasma is in the LTE and optically thin to radiation,

• The surrounding atmosphere is the argon plasma,

• The plasma flow is considered turbulent, transient, and axisymmetric. The turbulence is modeled using the LES model,

• The swirling component of jet velocity can be neglected comparison to the other components,

• Electric, magnetic and gravity forces and viscous heat dissipation are negligible.

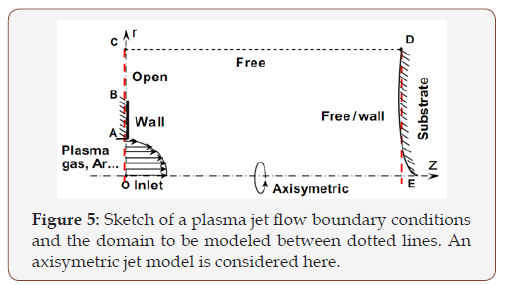
Plasma jet dynamics

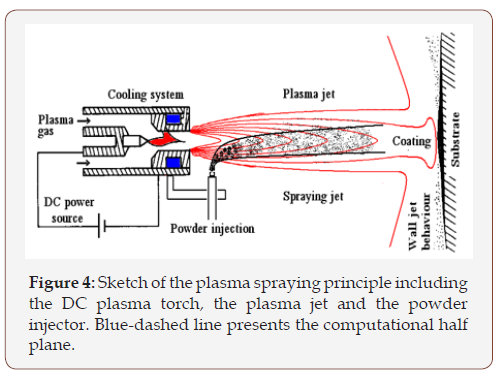
In this study argon plasma jet issuing into argon surrounding is simulated using a Fortran-based code developed for transient simulation of thermal plasma in axisymmetric coordinate system and uniform meshing. The calculation domain (Figure 4) is a halfsection containing the centerline axis. The flow problem is solved in a (x, y) standard LB formulation. In the LB dynamics, fluid particles’ moving differs from other particle based numerical methods such as dissipative pseudo particle dynamics, direct simulation Monte Carlo dynamics. In fact, particles occupying the discrete lattice nodes move from one node to the next in a streaming phase, then, particles collide and get a new speed in a collision phase. The simulation progresses in an alternation between the collision and the spread (streaming) of the particles. The present model consists of a 9-bits lattice for the hydrodynamic quantities and a 4-bits lattice for the thermal field to have finally a D2Q9-D2Q4 LB thermal model. The velocity vectors of such moving directions (Figure 3) are expressed as follows:

Where ζ is a unit velocity vector of the lattice. Following the two selected lattices, two populations of the LB equations based on single relaxation times (SRT) are used in this study. The time evolution equation of the density distribution function with source/ force term is written as [10]:

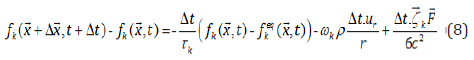
Where F_i=-ρ(u_iu_r/r+2υu_i/r²δ_ir), ω₀ = 4 / 9 , ϖ _k = 1/ 9 for k=1-4 and ω_k= 1/ 36 for k=5-8.

The Zhou’s revised-model is successfully extended here to thermal flow and then, similarly for the advection-diffusion equation of the scalar field, the LB equation is written as:

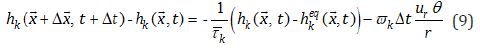
The new SRTs τ k and 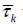used for the axisymmetric formulations are expressed as functions of the SRTs of the standard LB equations. With φ playing for υ and α , we have:

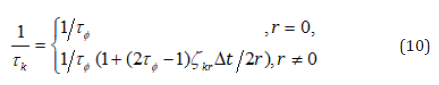
The SRTs of the standard LB equations are linked to the diffusion parameters as:

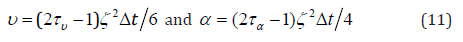
The fluid density ρ, velocity component ui and temperature θ are computed locally from the distribution function fk and gk in the same manner as that in the standard LB method for Cartesian coordinates which is the highest advantage of the Zhou’s revised model:

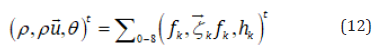
Where:

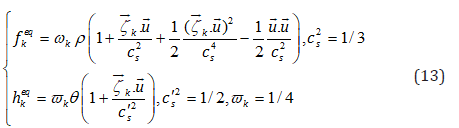
The continuity and Navier–Stokes equations can be recovered through the Chapman-Enskog expansion for the density distribution function. The final results of the Navier–Stokes equation and continuity equation are recovered as below [10]:

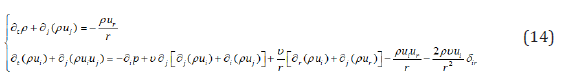
Under the low Mach number condition, 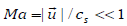, and if the density variation is assumed to be small enough, which is consistent with the LB dynamics, the above incompressible Navier- Stokes equation and continuity equation are rewritten as:

Besides, the plasma jet is laminar in its core but turbulent in its fringes due to the high field gradients (200 K/mm and 10 m/s/mm). In LBM-LES modelling of turbulence, only the collision relaxation time is locally readjusted, by adding the eddy viscosity to the molecular viscosity [11]. Note that in LB turbulence modeling, the local shear rate tensor ij S is available at each computational node without recourse to classic finite differencing.

For the chosen D2Q9 lattice, the effective relaxation time obeys the following equation:

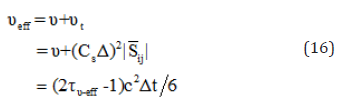
Note that in LB turbulence modeling, the local shear rate tensor 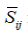is available at each computational node without recourse to classic finite differencing.

The computational domain is a half plane (Figure 4) sized in a 100mm 48mm in (z, r) cylindrical coordinates. The domain is mapped by uniform mesh in a 200 × 96 cells. The nozzle radius sizes 4 mm and its exit are governed by the following parabolic inlet conditions:

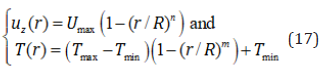
The boundary conditions on the remaining parts are given in Figure 5. The nozzle front face AB of the torch sizes 12mm. The Jets & Poudres [12] results are among others used to validate the present LB results either for the plasma jet or the powders dynamics and heating. In the solution procedure, the LB background, the turbulence modeling and the LB-physical conversion platform are considered and the thermo-physical properties temperaturevariation is fully accounted-for in our model [13].

Dynamic framework of conversion to physical space

In the following sections we dealt with some mono-dimensional and two-dimensional cases involving PDEs resolution n LB and dimensionless spaces.

We, consequently, presented the conversion procedure to return to physical space. This was even for constant or variable thermophysical properties.

Axisymmetric high temperature plasma jet

Plasma jets simulation are of many practical applications and are of many complexities due to the high temperature and velocities gradients especially near the nozzle exit and due to the extra nonlinearity of thermophysical properties with temperature as shown in Figure 1. The problem here is not to normalize and convert the physical variables (velocity, temperature, etc.) but to convert the transport properties (thermophysical parameters) themselves to their LB corresponding values that insure the variability with temperature and the stability condition of the relaxation time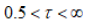

For the kinematic viscosity υ_Ph case (same for α_Ph) in D2Q9 lattice we have:

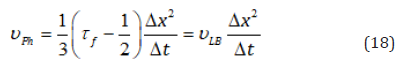
Using Equations (17) & (18), we can draw the conversion diagram. This procedure was applied to argon plasma jet. The boundary conditions may be found in Djebali [13]. The calculation chart is as follows:

The simulated results of argon plasma jet at 13500K for the conditions free are depicted in Figure (6 & 7).

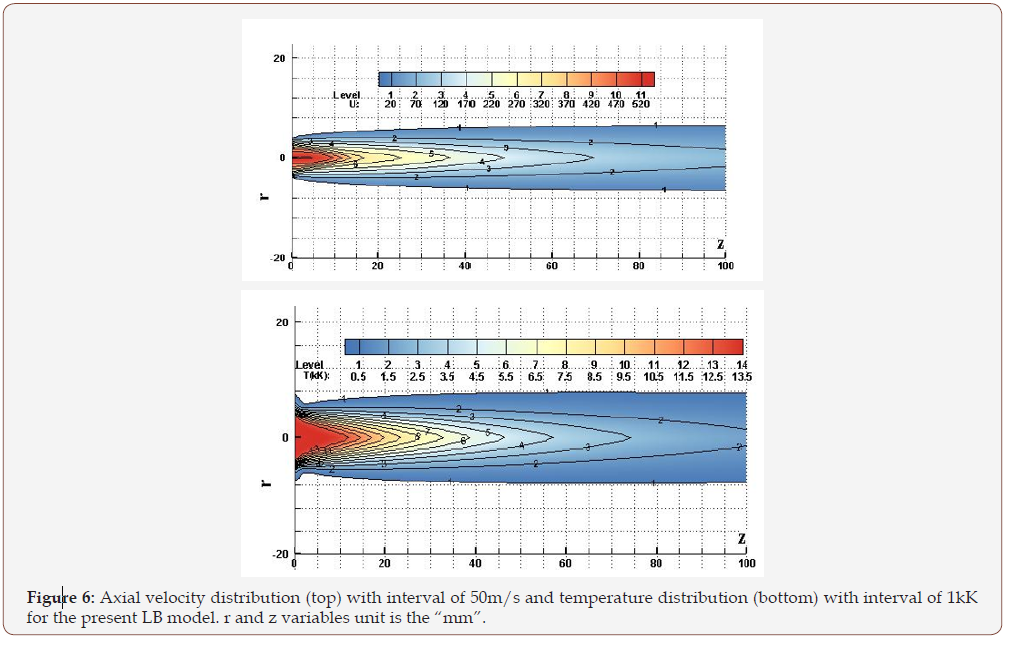
To show the validity of the proposed procedure of conversion and the novelty against others LB attempts to simulate this complex thermal flow, a validation analysis based on a free jet was performed. The centerline velocity and temperature profiles were compared to former predictions and measurements [12, 14-16]. The predicted results for the centerline axial velocity and temperature field are plotted in Fig. 7 and gathered with former works. As one can see, the LB results using the proposed conversion dynamic framework provide a good compromise between the Pfender and Jets & Poudres data, which use FV and FD numerical methods and different turbulence models.

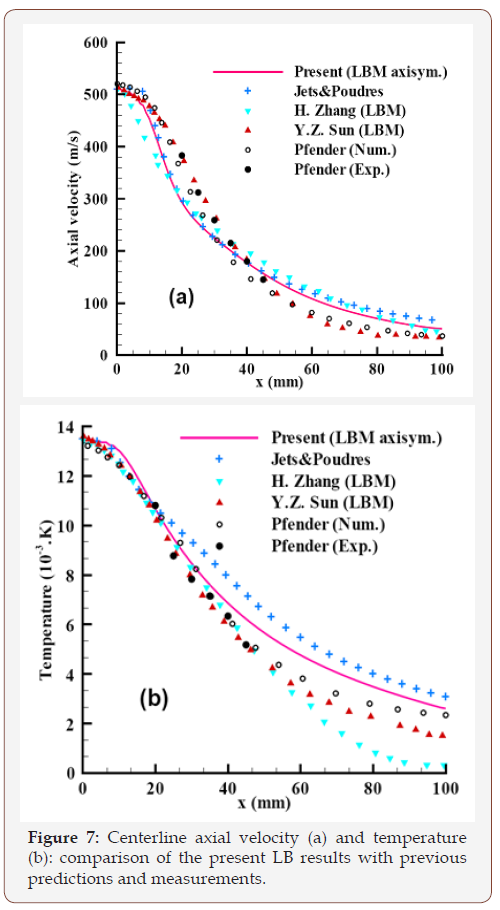
One can remark, also, that the axial temperature gradient near the inlet (interval 0-20mm) is close to 190 K/mm then close to 200 K/mm observed experimentally counter 136 K/mm and 152 K/mm for Jets&Poudres and Pfender results respectively and the velocity gradient is close to 8.8 (m/s)/mm counter 10.48 (m/s)/mm and 9.48 (m/s)/mm for Jets&Poudres and Pfender results respectively which agrees well with former experimental and numerical observations as noted here-above. It is also clear that our results go well with Jets&Poudres ones. The disparity between the two results in the potential core of the plasma jet (hot zone) is probably due to the fact that ramps are used in Jets&Poudres code for the inlet temperature and velocity profiles instead of our parabolic ones. After that, in the plasma jet core, the profiles become Gaussian and the two curves go together. However, the Zhang et al. [15] and Sun et al. [16] results using the Lattice Boltzmann method present significant discrepancy.

In the present study a framework-based lattice Boltzmann method for the simulation of turbulent argon plasma jets dynamics at very high temperatures was presented. The present case involves high temperature dependence of the thermophysical properties. It has been concluded from this study that:

• The thermophysical properties of the plasma gas are hugely varying as function of temperature in the range ambient temperature – 13500 K.

• The LBM computation of turbulent properties is very simply compared to conventional discretization methods and the convergence is reached in about 20000 iteration resulting in a CPU time of about five minutes for the chosen mesh resolution.

• The temperature and velocity gradients in the vicinity of the nozzle exit (0-20mm) are close to 190 K/mm and 8.8 (m/s)/ mm (respectively). Such a values are in excellent agreement with former observations from numerical predictions and measurements.

• The LB method results using the proposed model have shown excellent agreement with experimental and numerical results of classical methods (FDM, FVM). However, some deviations were found with others attempts of plasma jet simulations by the LB method as has been shown for the axial velocity and temperature profiles.

1. Lycett Brown D, Karlin I, Luo KH (2011) Droplet collision simulation by a multi-speed lattice Boltzmann method. Commun Comput Phys 9(5): 1219-1234.
2. Schmieschek S, Harting J (2011) Contact Angle Determination in Multicomponent Lattice Boltzmann Simulations. Commun Comput Phys 9(5): 1165-1178.
3. Djebali R, El Ganaoui M, Jaouabi A, Pateyron B (2016) Scrutiny of spray jet and impact characteristics under dispersion effects of powder injection parameters in APS process. Int Journal of Thermal Sciences 100: 229-239.
4. Inamuro T, Hayashi H, Koshiyama M (2011) Behaviors of spherical and nonspherical particles in a square pipe flow. Commun Comput Phys 9(5): 1179-1192.
5. He Bing, Chen Y, Feng W, Qing Li, Yang Wang et al. (2012) Compressible lattice Boltzmann method and applications. Int J Num Analysis & Modeling 9(2): 410-418.
6. Wu J, Huang JJ, Yan WW (2015) Lattice Boltzmann investigation of droplets impact behaviors onto a solid substrate. Colloids and Surfaces A: Physicochemical and Engineering Aspects 484(5): 318-328.
7. Tanaka Y, Washio Y, Yoshino M, Hirata T (2011) Numerical simulation of dynamic behavior of droplet on solid surface by the two-phase lattice Boltzmann method. Computers & Fluids 40(1): 68-78.
8. Gupta A, Sbragaglia M (2015) Deformation and break-up of Viscoelastic Droplets Using Lattice Boltzmann Models. Procedia IUTAM 15: 215-227.
9. Latifiyan N, Farhadzadeh M, Hanafizadeh P, Rahimian MH (2016) Numerical study of droplet evaporation in contact with hot porous surface using lattice Boltzmann method. Int Comm in Heat and Mass Transfer 71: 56-74.
10. Zhou JG (2011) Axisymmetric lattice Boltzmann method revised. Phys Rev E Stat Nonlin Soft Matter Phys 84(3 Pt 2): 036704.
11. R Djebali, M El Ganaoui, B Pateyron, H Sammouda (2011) Defect and diffusion Forum.
12. B. Pateyron, ‘Jets&Poudres’ and ‘T&Twinner’.
13. R. Djebali, Ph. D dissertation, (Univ. of Tunis el Manar -Tunisia & Univ. of Limoges - France, 2011), p. 99.
14. Pfender E, Chang CH (1998) Plasma Spray jets and plasma-particulate interaction: model-ing and experiments, In “Thermal spray: Meeting the Challenges of 21 Century” (C Coddet Ed), ASM International, Materials Park, OH, USA, pp. 315-327.
15. Zhang H, Hu S, Wang G, Zhu J (2007) Modeling and simulation of plasma jet by lattice Boltzmann method. App Math Mod 31(6): 1124-1132.
16. Sun YZ, Dang Y (2011) Numerical simulation of atmospheric pressure plasma jet using lattice Boltzmann method. Applied Mechanics and Materials 44(47): 1838-1842.