 Research Article
Research Article
Initial Yield Surface of Shape Memory Alloy in Stress Induced Martensitic Phase Transformation
JJ Zhu1*,WM Huang2, and KM Liew3
1School of Civil Engineering and Architecture, Wuyi University, China
2School of Mechanical and Aerospace Engineering, Nanyang Technological University, Singapore
3Department of Architecture and Civil Engineering , City University of Hong Kong, Kowloon, Hong Kong
JJ Zhu, School of Civil Engineering and Architecture, Wuyi University, China.
Received Date: August 28, 2018; Published Date: September 24, 2018
Abstract
Based on the critical conditions for nucleation and the actual eigenstrain of a given shape memory alloy in the stress induced martensitic phase transformation, the closed-form expression of its corresponding initial yield (nucleation) surface is obtained. Consequently, the underline mechanism for non-symmetry in the stress vs. strain relationship between uniaxial tension and uniaxial compression experimentally observed in many SMAs is revealed. Unlike that in many traditional criteria, such as the Von Mises and Tresca criteria, in which the yield surfaces are functions of stress only, the yield surface derived here is closely related to the crystal structures before and after the phase transformation. The initial yield surface of a polycrystalline CuZnAl shape memory alloy tube under combined loading of tension and torsion predicted by the formula developed here agrees well with the experimental results reported in the literature.
Keywords: Shape memory alloy; Phase transformation; Microstructure; Yield surface
Introduction
The thermomechanism behind shape memory phenomenon in Shape Memory Alloy (SMA) is a significant amount of shear strain upon phase transformation. It is well known that such phase transformation can be induced either by temperature (known as thermally induced phase transformation) or by stress (stress induced phase transformation). As a result of this unique shape memory behavior, SMAs have been used in various applications for some years [1].
So far, there are still a few questions on the behavior of SMA waiting to be solved. Asymmetry in tension and compression of SMAs is one among others [2-7]. Experiments under combined loads of tension and torsion have been carried out on NiTi [8] and CuZnAl [9]. From these tests, it is observed that, in general, the yield (transformation start stress in stress induced phase transformation) surface of SMA cannot be described either by Von Mises criterion or by Tresca criterion. Therefore, it turns to be an interesting phenomenon for further investigation.
In this paper, based on the critical condition of nucleation and corresponding eigenstrain in austenite to martensite phase transformation, the initial yield surface of SMA is investigated. The resulting yield surface of polycrystalline CuZnAl (in tube shape) under combining tension and torsion loads is compared with the experimental result reported in the literature.
Phase Transformation Eigen-strain and Critical Condition for Nucleation
It is assumed here that the austenite finish temperature of a polycrystalline SMA is Af . In the absence of external stress, at temperature T (T > Af ) this SMA is 100% austenite. Provided that a stress state Σ is applied on it and then gradually increased. As long as Σ reaches a certain level, stress induced phase transformation starts. This is called nucleation in material science. The resulting martensite is known as martensite Habit Plane Variant (HPV).
In some SMAs, for instance, CuZnAl, the martensite HPV is Lattice Correspondence Variant (LCV). But in some other SMAs, such as NiTi and CuAlNi, HPV is formed by a pair of twinned LCVs. Readers may refer to reference by Saburi and Nenno [10] for details of the relation among martensite variant, HPV and LCV.
Let us take a Representative Volume Element (RVE) from this
polycrystalline SMA. Assume that this RVE includes N grains. Under
a given stress state Σ , in grain k (1 ≤ k ≤ N ), up to 24 martensite
HPV may be produced. Provided that the phase transformation
eigenstrain of l th martensite HPV ( 1 ≤ l ≤ 24) is given by 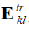 , the
work done by external stress to produce this martensite HPV may
be expressed as [11]
, the
work done by external stress to produce this martensite HPV may
be expressed as [11]

Therefore, the thermodynamic driving force (Π) can be written as

Here, U(T) is the thermodynamic driving force due to chemical free energy and interaction energy etc. In the literature, U(T) are presented in slightly different forms [12-28]. Despite the difference, the fact is that U(T) depends only on temperature T and volume fraction of martensite variant (but not on applied stress Σ ). Well known Clausius-Clapyron equation [11,29,30] can be derived from Equation (2). Thus, at a given temperature T, the condition for nucleation is given by

An equivalent form may be written as

Recall previous assumption, this SMA is initially pure austenite. The surface of nucleation stress is termed initial yield surface in this paper. If yield just starts (nucleation), only one martensite HPV is induced. Thus, the nucleation criterion may be written as
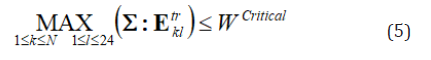
where the maximum is over all possible phase transformation eigenstrains of martensite HPV, i.e., overall k (1 ≤ k ≤ N ) and l ( 1 ≤ l ≤ 24 ). Equation (5) can be reduced to
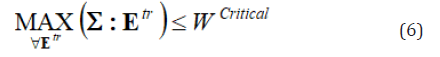
Equations similar to Eqs. (2) & (6) have been applied in studies on both single crystalline and polycrystalline SMAs. To name a few, papers [31-36] are based on similar principle.
In martensite phase transformation, deformation of habit plane variants may be shown as Figure 1, where n is normal vector of habit plane, and b is shape strain vector. In general, the transformation eigenstrain of SMA includes not only shear deformation, but also a small dilatation. Therefore, shape strain vector b is normally not perpendicular to unit normal vector of habit plane n . Decompose vector b into two parts: one is in n direction, and the other is vertical to n , i.e.,

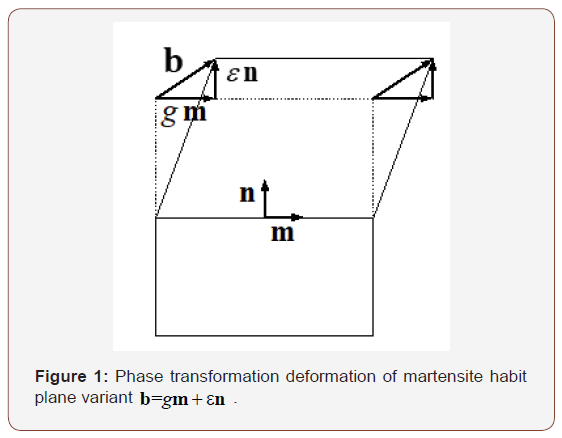
It is known that both g and ε depend only on lattice parameters (i.e. microstructures) of austenite and martensite, but not on the orientation of martensite HPV. Suppose that the deformation of martensite HPV is F , then

in which I is identity tensor. The right Cauchy-Green strain tensor of martensite HPV is given by (Ball and James 1987)
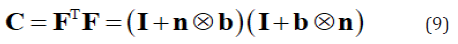
The phase transformation eigenstrain of martensite HPV may be written as
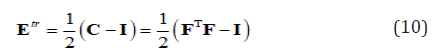
Substituting Eq. (5) into Eq. (10) yield
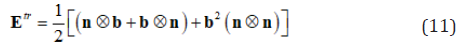
From Eq. (7)

Substituting Eq. (12) into Eq. (11) yields
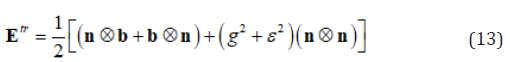
Substituting Eq. (7) into Eq. (13) yield
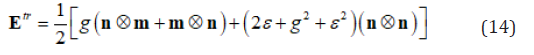
Let

and
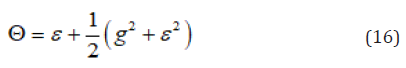
Eq. (14)-(16) yield

It is noted that in Eqs. (11), (13) or (17), the second term is nonlinear term. In previous literatures [12,18] among others, it is believed that the nonlinear terms can be ignored, thus Eq. (13) reduce to
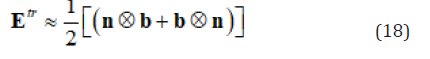
Or equivalently Eq. (16) reduce to

From the point view of calculation, the approximate value of Eigen-strain phase transformation, Eq. (18) is acceptable. In present paper, we focused on the shape of yield surface, as we will see late, yield surface is sensitive on parameter Θ, thus the nonlinear term of phase transformation eigen-strain plays an important ruler in yield surface, ignore nonlinear terms may result in a wrong yield surface. In some of literature [34,35] the work done by external stress is calculated by
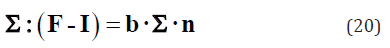
In fact, from Eq. (18) we also obtain

It is apparently that (F - I) is not frame independent (i.e. it is not a tenser), thus, it cannot be taken as strain measurement. In both of above two approximate calculations, the nonlinear terms are ignored. It may result in a wrong yield surface.
The maximum of Eq. (6) is over all possible pairs of n and m (n2 = 1, m2 = 1 and n ⋅m = 0 ). Substituting Eq. (17) into Eq. (6), the nucleation condition becomes
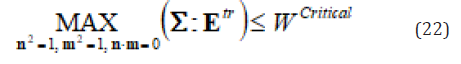
Subsequently,
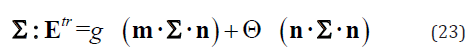
If taking rectangular Cartesian coordinate system o − e1 e2 e3 along the directions of principal stresses σ1 ,σ2and σ3, (σ1 ≥σ2≥σ3 then
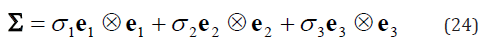
Let
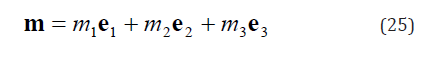
and
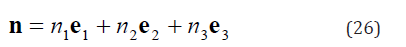
From Eqs. (23)-(26)
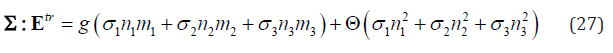
where n and m satisfy the following conditions,
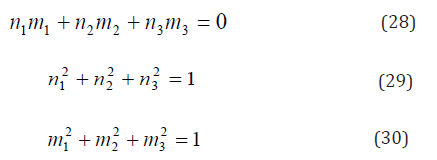
From Eqs. (27)-(30)
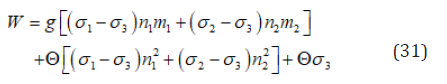
Define

It is apparent that to find the maximum of Π is equivalent to find the maximum of W , and also equivalent to find the maximum of Λ .
Define

From Eqs. (31)-(34)
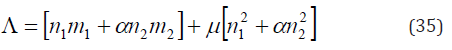
Hence, the original problem turns to find the maximum of Eq. (35) under the constrain conditions given by Eqs. (28)-(30). Introduce Lagrange multiply fractions λ1, 2λ, 3λ and
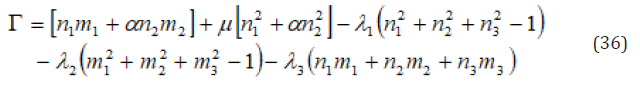
The condition for maximum Γ is
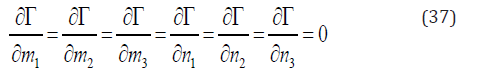
i.e.,
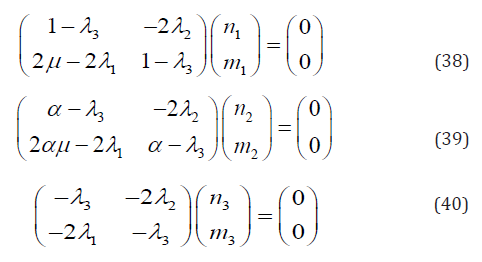
By solving simultaneous Eqs. (28)-(30) & (38)-(40), and substituting the solution into Eq. (36), the maximum Γ can be obtained.
Let
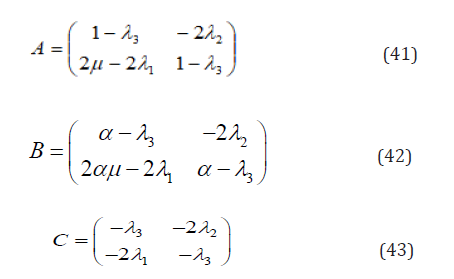
It can be proved that the maximum value of Γ does not exist, if any two of A , B and C are non-singular.
For instance, if detA ≠ 0 and detB ≠ 0 , Eqs. (38) & (39) give
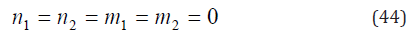
From Eqs. (29) & (30)

It is apparent that Eqs. (44) & (45) cannot result in the maximum Γ .
Maximum Λ
From the discussion above, we know that there are four possible ways to get maximum Λ , i.e. A, B, and C are all singular, or only one of A, B and C is non-singular. All these four cases are studied in following four subsections respectively.
Matrixes A , B and C are all singular
In this case,
By substituting Eqs. (41)-(43) into Eq. (46), one can see that if Eq. (46) has solution, either α = 1 or α = 0 . In both cases
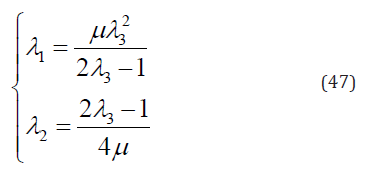
From Eqs. (47) and (38)-(40)
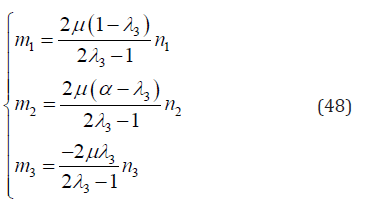
If α = 1: From Eq. (48), Eqs. (28)-(30) yield

Re-writing the second formula of Eq. (49) gives

Subsequently the first formula in Eq. (49) becomes

and the third formula in Eq. (49) turns to be
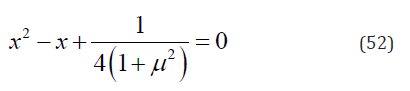
Hence, the results of Eq. (52) are
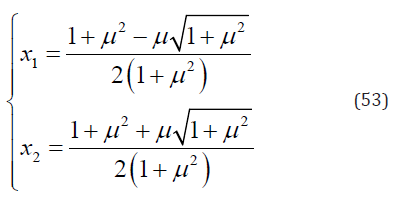
Substituting Eqs. (48) & (50) into Eq. (35) yields

Substituting x = x1 into Eq. (54) yields
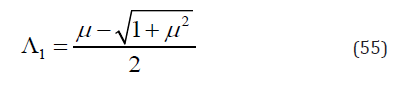
Substituting x = x2 into Eq. (54) yields
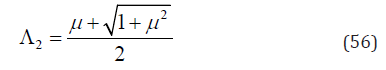
It is noticed that Λ2 > Λ1. Thus, the maximum Λ is
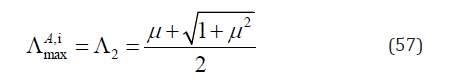
If α = 0 : According to Eq. (48), Eqs. (28)-(30) can be re-written as
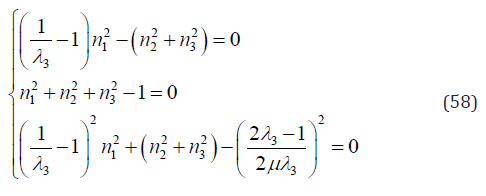
The second formula in Eq. (58) may be rewritten as
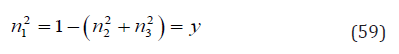
Therefore, the first formula in Eq. (58) becomes

and the third formula in Eq. (58) is
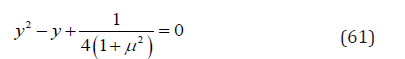
The results of Eq. (61) are
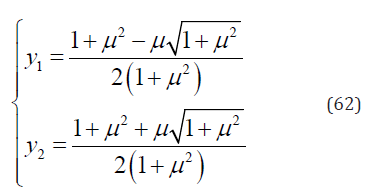
Substituting Eqs. (48) & (59) into Eq. (35) gives

Substituting of y = y1 into Eq. (54) gives
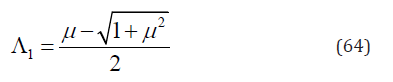
Substituting of y = y2 into Eq. (54) gives
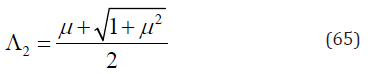
As Λ2 > Λ1 , the maximum Λ is
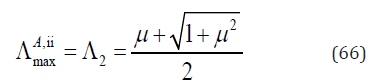
This is same as Eq. (57). So the maximum Λ for both α = 0 and α = 1 is
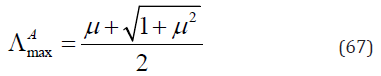
Matrix is non-singular
In this case both B and C are singular, but

From Eqs. (68) & (38)

Equation (35) becomes
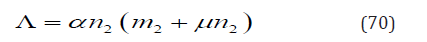
From

λ1a and λ2 may be presented as functions of λ3
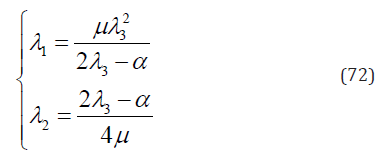
Substituting Eq. (72) into Eqs. (39)-(40) yields
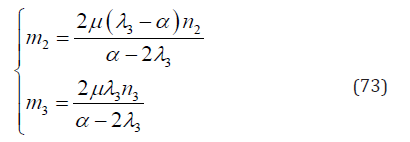
Substituting Eqs. (69) & (73) into Eqs. (28)-(30) yields
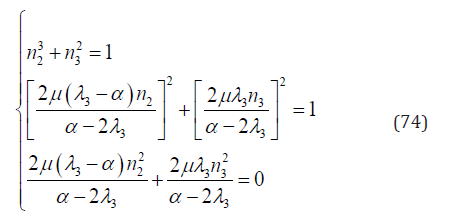
Solving Eq. (74) results in the following eight groups of solution for variables n2 ,n3 and λ3
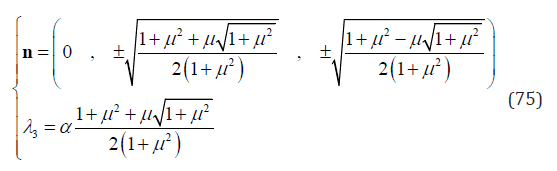
and
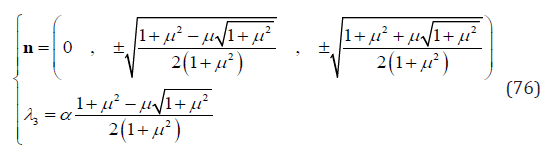
Using Eqs. (73), (75) & (76), m2 and m3 can be solved. Substituting these eight groups of solution one by one into Eq. (70), and then comparing them, the maximum Λ is obtained as
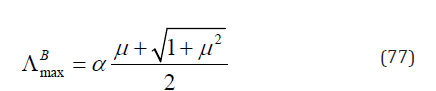
Matrix B is non-singular
In this case both A and C are singular, but

Eqs. (78) & (39) yields

Equation (35) becomes
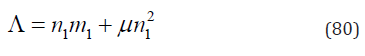
Since
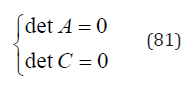
one may express λ1 and λ2as functions of λ3, i.e.,
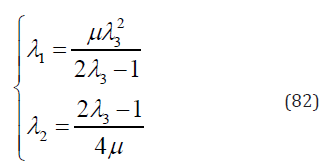
Substituting Eq. (82) into Eqs. (38) & (40) yields
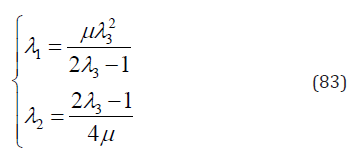
Substituting Eqs. (79) & (83) into Eqs. (28)-(30) yields
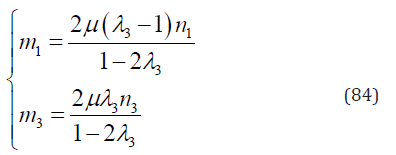
Eight groups of solution for variables n1,n3 and λ3 are resulted from Eq. (84). There are
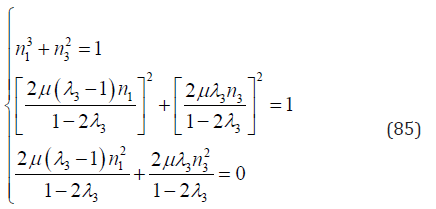
and
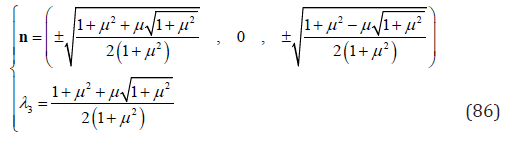
m1 and mn3 can be solved from Eq. (83). Substituting these eight groups of solution one after another into Eq. (80), we get the maximum Λ as
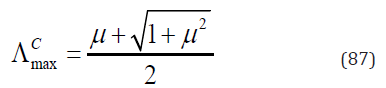
Matrix C is non-singular
In this case, both A and B are singular, but

From Eqs. (88) & (40), we obtain

As

λ1 and λ2 can be expressed as functions of λ3 ,
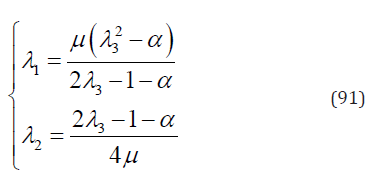
Substituting Eq. (91) into Eqs. (38)-(39) yields
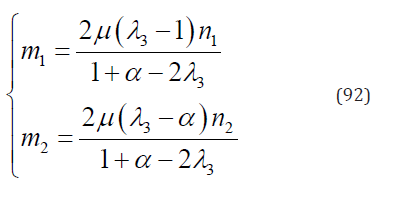
Substituting Eqs. (79) & (83) into Eqs. (28)-(30) yields
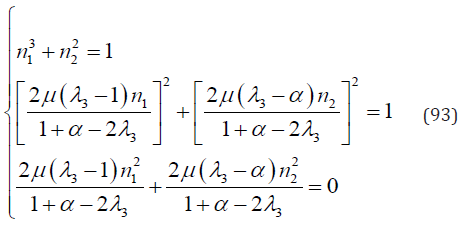
By solving Eq. (93), eight groups of n1, n2 and λ3 are resulted. They are
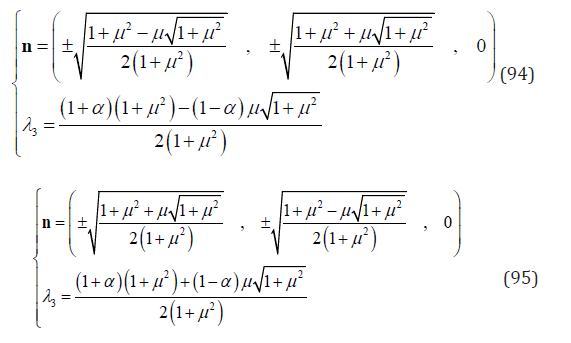
From Eq. (92), m1 and m2 are obtained. Substituting these eight groups into Eq. (35), the maximum of Λ is given by
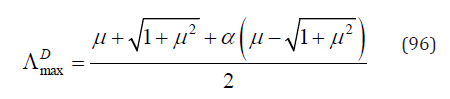
Yield Surface
As shown previously, if α = 1 or α = 0 ,
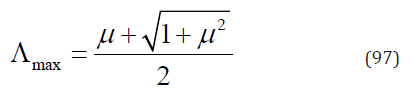
On the other hand, if α ≠ 1 and α ≠ 0 , according to Eqs. (77), (87) & (96)
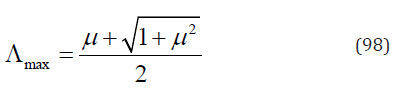
Therefore, for whatever the case,
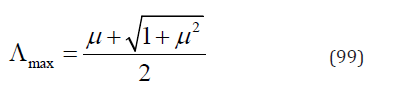
It is surprising to see that Λmax has nothing to do with α. It means that Λmax is independent on the applied load.
From Eq. (32), we haveM
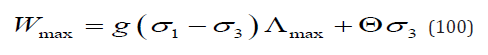
Substituting Eq. (34) and Eq. (99) into Eq. (100) we have
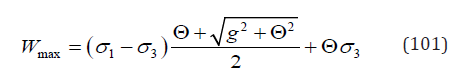
Since the nucleation condition is given by
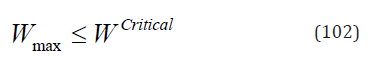
i.e. the yield criterion reads
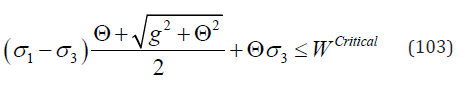
Denote
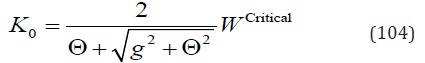
then Eq. (103) may be expressed as
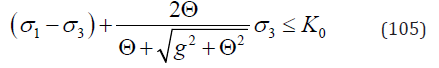
Denote
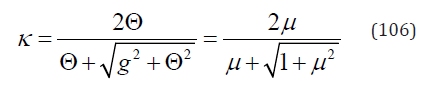
then, Eq. (105) can be written as

If ε = 0 (i.e. no dilation), Eq. (16) becomes

Substituting Eq. (107) into Eq. (106) we have
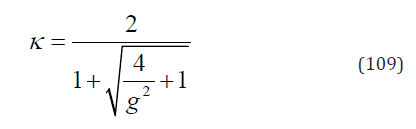
Notice that g2 << 1, thus κ ≈ 0 . If κ = 0 then Eq. (107) is reduced to

This is Tresca criterion.
We can express the resolved shear stress as

If ε = 0, by substituting Eq. (23) into Eq. (6), Eq. (6) reduces to

Equation (98) is in a similar form as Schmid law [37]. It indicates that Tresca criterion that is empirical in nature can be derived from Schmid law.
Let
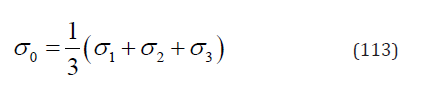
Equation (108) may be expressed in terms of σ0 and α as
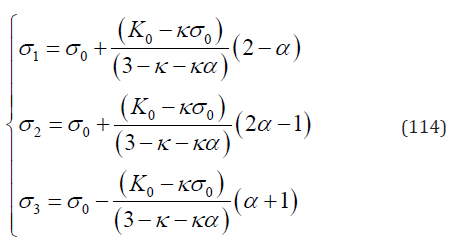
where 0 <α < 1 and σ1≥σ2≥σ3.
In order to obtain a complete yield surface, the whole principal stress space is divided into six sections as shown in Figure 2. By swapping the positions of σ1, σ2 and σ3 , the yield surfaces in other five sections can be produced from yield surface in one section that is available.
Case Study
The case studied here is CuZnAl polycrystal. The transformation is from cubic to monoclinic ( DO3 →6M ). Its lattice parameters are measured by Chakravorty & Wayman [38] as a0 = 0.5996 (nm ) , a = 0.4553 (nm ), b = 0.5452 (nm ), c = 3.8977 (nm ), and θ = 87.5o . The phase transformation eigenstrains have been calculated in literature [21,26,39,40]. Unit normal vector of habit plane n and shape strain vector b have been calculated in reference paper [21,26] based on Eqs. (14) & (15). They are
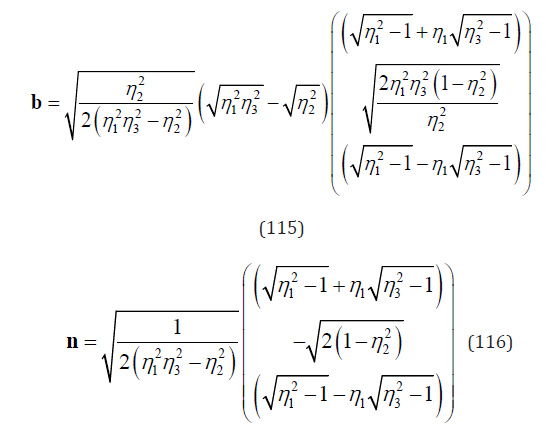
where
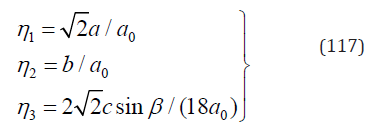
From Eq. (7) we have

and

Substituting Eqs. (115)-(116) into Eqs. (118) & (119) result in ε = -0.0036 and g = 0.1866 . Substituting g and ε into Eq. (16), we have Θ = 0.0138 , From Eqs. (34), we have μ = 0.074 . From Eq. (106), we have κ = 0.1378 .
Yield surface can be produced by substituting the value of κ into Eq. (107). Resulting yield surface against Treseca yield surface is shown in Figure 3.
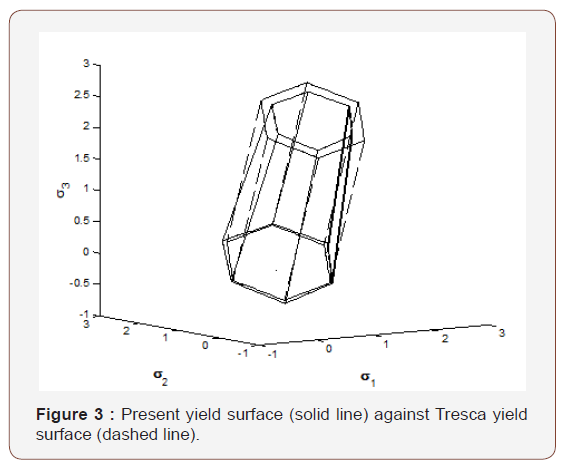
From Eq. (103) it is known that if Θ = 0 , the yield surface reduces to Treseca yield surface. The non-symmetry of materials in tension and compression is dependent upon the difference between real yield surface and Treseca yield surface, therefore it sensitively relates with parameter Θ . From Eq. (16) it is known that Θ contain two parts, first part ε result from volume variation during phase transformation, and second part result from nonlinear property of phase transformation Eigen-strain. Numerical calculation shows that nonlinear term of phase transformation Eigen-strain sometime may large than volume variation during phase transformation. Thus, it cannot be ignored.
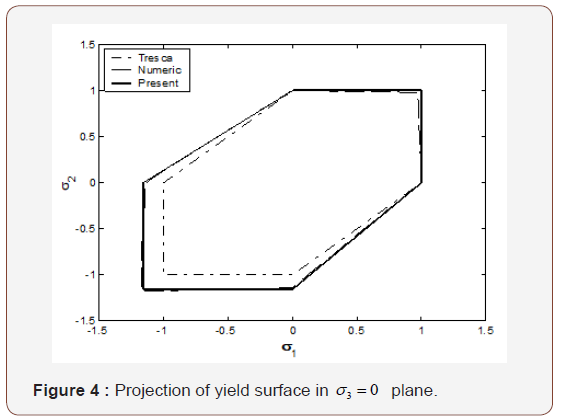
It is noticed that, if Θ ≠ 0 , the size of yield surface projected in π -plane depends on the hydraulic press σ0. Yield surface of CuZnAl in biaxial stress (σ2 = 0) plane is plotted in Figure 4. The numerical result is obtained by using the scheme proposed in reference paper [34]. 29791 grains are used in the calculation. And the transformation strain in numerical study is calculated by (UTU − I)/ 2 instead of (F − I). Here, U is taken from reference paper [39].
The yield strength of a thin polycrystalline CuZnAl round tube under combining tension and torsion loads has been tested and reported in reference paper [9]. Let σ stands for extension stress and τ for shear stress. The corresponding principal stresses are
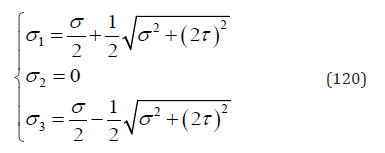
Substituting Eq. (120) into Eq. (107), the initial yield surface becomes
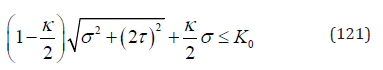
If κ = 0 , Eq. (121) turns to be Tresca yield surface,

On the other hand, standard Von Mises yield surface is given by

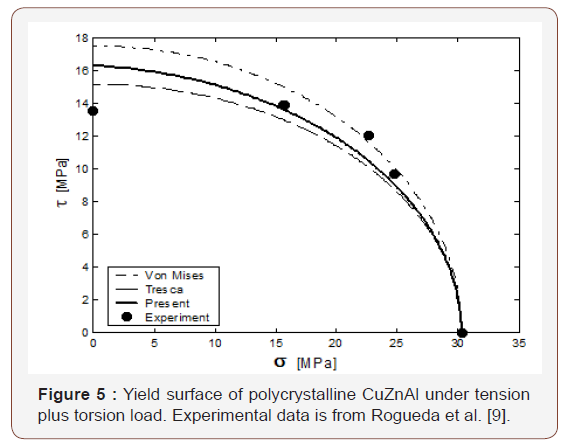
The yield surfaces by Eqs. (121)-(123) are plotted against the experimental results in Figure 5. As we can see, except one point which corresponding to pure torsion, the proposed surface is closer to the testing result than other surfaces.
Conclusion
Based on the critical condition for nucleation and eigenstrain in stress induced martensitic transformation, the initial yield (nucleation) surface of SMA is derived. A simple close form solution is given. This method provides not only a simple way to explain the non-symmetry in tension and compression of many SMAs, but also a convenient way to predict the yield surface of SMA. The result differs from tradition criterion, such as Von Mises and Tresca, in two aspects. First, it is in terms of not only stress but also parameters of microstructure. Second, it is solely derived from crystal parameters. It shows a clear and strong relationship between crystalline structure and yield surface. Yield surface not only dependent up volume variation but also dependent upon nonlinear term of shear deformation. The resulting initial yield surface of CuZnAl thin tube under tension plus torsion load agrees well with the experimental result reported in the literature.
References
- Funakubo H (1987) Shape memory alloys. (Gorden and Breach Science Publishers).
- Orgeas L, Favier D (1995) Non-Symmetric Tension-Compression Behaviour of NiTi Alloy. Journal de Physique IV 5(C8): 605-610.
- Otsuka K, Shimizu K (1974) Morphology and Crystallography of Thermoelastic Cu-Al-Ni Martensite Analyzed by Phenomenological Theory. Transactions of the Japan Institute of Metals 15(2): 103-108.
- Otsuka K, Shimizu K (1982) Proceedings of an International Conference on Solid to Solid Phase Transformations Metallurgical Society of AIME, USA, pp. 1268-1286.
- Pelton AR, Rebelo N, Duerig TW, Wick (1994) Experimental and FEM Analysis of the Bending Behaviour of Superelastic Tubing. The First International Conference on Shape Memory and Superelastic Technologies, pp. 353-364.
- Sittner P, Takakura M, Hara Y, Tokuda M (1996) On Transformation Pathways of General Stress Controlled Thermoelastic Martensitic Transformation in Shape Memory Alloys. Journal de Physique Archives 6(C1): 357-366.
- Plietsch R, Ehrlich K (1997) Strength differential effect in pseudoelastic NiTi shape memory alloys. Acta Materialia 45(6): 2417-2424.
- Berg B (1997) Twist and stretch: combined loading of pseudoelastic NiTi tubing. Proceedings of the Second International Conference on Shape Memory and Superelastic Superelastic Technologies (SMST-97): 443-448.
- Rogueda C, Lexcellent C, Bocher L (1996) Experimental study of pseudoelastic behaviour of a CuZnAl polycrystalline shape memory alloy under tension-torsion proportional and non-proportional loading tests. Arch Mech 48(6): 1025-1045.
- Saburi T, Nenno S (1982) Proceedings of the International Conference on Solid-Solid Phase Transformations (eds, DE Laughlin, RF Sekerka, CM Wayman), pp. 1455-1479.
- Horikawa H, Ichinose S, Morii K, Miyazaki S, Otsuka K (1988) Orientation dependence of β1 → β1 stress-induced martensitic transformation in a Cu-AI-Ni alloy. Metallurgical and Materials Transactions A 19(4): 915- 923.
- Boyd JG, Lagoudas DC (1996) A thermodynamical constitute model for shape memory materials .1. The monolithic shape memory alloy. International Journal of Plasticity 12(6): 805-842.
- Gall K, Sehitoglu H (1999) The role of texture in tension-compression asymmetry in polycrystalline NiTi. International Journal of Plasticity 15(1): 69-92.
- Huang M, Brinson LC (1998) Multivariant model for single crystal shape memory alloy behavior. Journal of the Mechanics and Physics of Solids 46(8): 1379-1409.
- Huo Y, Muller I (1993) Nonequilibrium Thermodynamics of Pseudoelasticity. Continuum Mechanics and Thermodynamics 5(3): 163-204.
- Patoor E, Berveiller M (1997) Mechanics of Solids with Phase Changes. M Berveiller, FD Fischer (Eds.), Springer Vienna, Austria, pp. 121-188.
- Patoor E, Berveiller M (1999) Micromechanical modelling of the thermomechanical behavior of shape memory alloys. International Centre for Mechanical Sciences 368: 121-188.
- Patoor E, Eberhardt A, Berveiller M (1996) Micromechanical modelling of superelasticity in shape memory alloys. Journal De Physique IV Colloque 6(C1): 277-292.
- Patoor EE, A Berveiller M (1998) Thermomechanical modelling of shape memory alloys. Archives of Mechanics 40: 775-794.
- Zhu J, Liang N, Huang W, Liew KM, Liu Z (2002) A thermodynamic constitutive model for stress induced phase transformation in shape memory alloys. International Journal of Solids and Structures 39(3): 741-763.
- Zhu JJ, Huang WM, Liew KM (2002) To Describe the Deformation from DO 3 Austenite to 18R Martensite in Shape Memory Alloys using Group Theory. IUTAM Symposium on Mechanics of Martensitic Phase Transformation in Solids: Proceedings of the IUTAM Symposium held in Hong Kong, China, pp. 163-170.
- Zhu JJ, Huang WM, Liew KM (2003) Deformation energy in martensitic transformation. J. Phys. IV France 112: 179-182.
- Zhu JJ, Liang NG, Cai M, Liew KM, Huang WM (2008) Theory of phase transformation and reorientation in single crystalline shape memory alloys. Smart Materials and Structures 17(1).
- Zhu JJ, Liang NG, Huang WM, Liew KM (2001) Energy conversion in shape memory alloy heat engine - Part II: Simulation. Journal of Intelligent Material Systems and Structures 12(2): 133-140.
- Zhu JJ, Liang NG, Liew KM, Huang WM (2001) Energy conversion in shape memory alloy heat engine - Part I: Theory. Journal of Intelligent Material Systems and Structures 12(2): 127-132.
- Zhu JJ, Liew KM (2003) Description of deformation in shape memory alloys from DO3 austenite to 18R martensite by group theory. Acta Materialia 51(9): 2443-2456.
- Zhu JJ, Liew KM (2004) Describing the Morphology of 2 H Martensite Using Group Theory Part I: Theory. Mechanics of Advanced Materials and Structures 11(3): 197-225.
- Zhu JJ, Liu QY, Huang WM, Liew KM (2004) To simulate the behavior of shape memory alloys under thermomechanical cycling. Materials Science and Engineering A 365(1,2): 298-301.
- Wollants P, Roos JR, Delaey L (1993) Thermally- and stress-induced thermoelastic martensitic transformations in the reference frame of equilibrium thermodynamics. Progress in Materials Science 37(3): 227- 288.
- Wayman CM, Duerig TW (1990) Engineering Aspects of Shape Memory Alloys (eds TW Duerig, KN Melton, D Stockel, CM Wayman) Butterworth- Heinemann, pp. 512.
- Buchheit TE, Wert JA (1996) Predicting the orientation-dependent stress-induced transformation and detwinning response of shape memory alloy single crystals. Metallurgical and Materials Transactions A 27(2): 269-279.
- Buchheit TE, Kumpf SL, Wert JA (1995) Modeling the stress-induced transformation behavior of shape memory alloy single crystals. Acta Metallurgica et Materialia 43(11): 4189-4199.
- Comstock RJ, Buchheit TE, Somerday M, Wert JA (1996) Modeling the transformation stress of constrained shape memory alloy single crystals. Acta Materialia 44(9): 3505-3514.
- Huang W (1999) “Yield” surfaces of shape memory alloys and their applications. Acta Materialia 47(9): 2769-2776.
- Shield TW (1995) Orientation Dependence of the Pseudoelastic Behavior of Single-Crystals of Cu-Al-Ni in Tension. Journal of the Mechanics and Physics of Solids 43(6): 869-895.
- Somerday M, Comstock RJ, Wert JA (1997) A systematic analysis of transformation stress anisotropy in shape memory alloys. Philosophical Magazine A 75(5): 1193-1207.
- Kocks F (1970) The relation between polycrystal deformation and single-crystal deformation. Metallurgical and Materials Transactions B 1(5): 1121-1143.
- Chakravorty S, Wayman CM (1977) Electron microscopy of internally faulted Cu-Zn-Al martensite. Acta Metallurgica 25(9): 989-1000.
- Bhattacharya K, James RD (1999) A theory of thin films of martensitic materials with applications to microactuators. Journal of the Mechanics and Physics of Solids 47(3): 531-576.
- Pitteri M, Zanzotto G (1998) Generic and non-generic cubic-tomonoclinic transitions and their twins11 Dedicated to Prof. I. Muller on his 60th birthday. Acta Materialia 46: 225-237.
-
JJ Zhu, WM Huang, KM Liew. Initial Yield Surface of Shape Memory Alloy in Stress Induced Martensitic Phase Transformation. Glob J Eng Sci. 1(1): 2018. GJES.MS.ID.000505.
-
Yield surface, Shape memory alloy, Martensitic phase transformation, Phase transformation, Microstructure, Thermomechanism, Eigen-strain, Critical condition for nucleation, martensite habit plane variant, Maximum Λ, π – plane, Tresca yield, Crystalline structure, Parameter, Polycrystalline, Eigen-strain, Tresca criterion, Cauchy-Green strain tensor of martensite, Lattice parameters, Temperature
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






