Discrete Model of Three Interacting Pacemakers Taking into Account the Time of Refractoriness as Applied to The Activity of Cardiac Fibrillation

The kinetics of the chaos and cardiac arrhythmia

Heart muscle (like any other muscle tissue) refers to the so-called excitable systems. Wave propagation in such systems is carried out by means of an energy source distributed in it. When a pulse is applied to such a system from the place of its application, a perturbation begins to propagate - the excitation wave: the incoming pulse is transmitted from the element to the element without damping sequentially. Usually, after excitation, each element is not able to immediately be excited again. As a rule, there is a certain “relaxation time”, called the refractory period, during which the element as it is restored. This lead, on the one hand, to an ordered spatial propagation of the excitation wave, and on the other hand, with frequent supply of pulses (or with a large period of refractoriness), some of them will be blocked. In the description of a number of excitable media often resort to the approximation of the original system a set of individual excitable elements, locally interacting with each other. Each such element is capable of being in one of three States - rest, excitation and refractoriness. From the state of rest, the element can go into an excited state, in which there will be a certain time. Then he goes into a state of refractoriness and only then again in a state of rest. Thus, the transition to the excited state is possible only from the state of rest. Although this model is a certain approximation, it very well reproduces the main phenomena in excitable media, including in the tissues of the heart. Suppose that there is a homogeneous excitable medium in which all elements have identical properties. Then the excitation frequency of all such elements will be the same. If some area of this environment to start periodically to perturb, in this region there is a source of concentrically radiating waves of excitement. Such a source is called a leading center or pejjsmeker. If an excitable medium is two or more pacemaker, the pejjsmeker less of the oscillation frequency with time is suppressed by pejjsmeker greater frequency. In other words, there is competition between pacemakers. Ideally, after a certain time, only one pacemaker will remain in the entire environment. In addition to pacemakers, in excitable media may appear other sources of excitation - spiral waves, which are “rotating” spiral. All spiral waves have the same frequency. Therefore, they always coexist with each other, but extinguish the leading center, which is a slower autowave source. In addition, spiral waves are the main type of elementary self- supporting structures in homogeneous excitable media. Like vortices in a superconductor or in superfluid helium, they are extremely stable. The appearance of several sources of excitation in the heart muscle is currently associated with dangerous disorders of the normal functioning of the heart - arrhythmia. With a large number of abnormal sources, fibrillation occurs. Let’s say that in some medium available only main and additional leading centers. Then even such a simple situation, depending on the frequency of the pulses and the refractoriness time, can lead to a very complex behavior of the medium. In particular, there may be quasi-periodic and chaotic dynamics. Thus, the emergence of only one parasitic pacemaker for the excitable system can lead it to spontaneous behavior. A much more dangerous cardiac arrhythmia - fibrillation - is caused by the appearance of many small waves in the heart tissue. This process can develop due to several reasons. One of them is the appearance of periodic stimulation of myocardial areas. In this case, fibrillation occurs after the cessation of stimulation in a medium with a variable refractory period. If, for one reason or another, the heart received a pulse in the critical phase (during the refractory period of the ventricles), it will generate a wave crossing the refractory zone. Then the ends of the excitation wave can twist, giving rise to spiral waves rotating in opposite directions. Modern methods of removing the heart from the state of fibrillation are very rigid (supply of a short electrical pulse of a huge voltage and a large current). The development of nonlinear dynamics and synergetic made it possible to understand that such a force effect is not necessary. Often enough weak electrical effects directly on the heart muscle. Precisely, if there are spiral waves with opposite directions of rotation in the medium, then, choosing the phase and frequency of external action, it is possible to achieve the movement of the centers of the two waves towards each other and their annihilation. Now the word for careful experimental research.

Arrhythmia

Heart rhythm is not a strictly periodic process, since the heart muscle is not an isolated system. In a healthy state, the heart always responds to physical activity, respiratory rhythm, etc. [1]. Moreover, periodic excitation of the heart indicates pathology, and strictly regular contractions of the heart can lead to its sudden stop and, as a consequence, to the death of the body (see, for example, [2]). However, arrhythmias are a completely different kind of aperiodic behavior of the heart. In this case, the heart muscle is no longer amenable to simple control with the help of incoming impulses.

Arrhythmia is any heart rhythm that differs from the normal sinus rhythm by changes in the frequency and regularity of the source of excitation of the heart, as well as by a violation of the conduction of impulses. From this point of view, arrhythmias can be divided into three large groups. One of them is arrhythmias due to violation of the passage of impulses. For example, atrioventricular heart block may be characterized by abnormal coordination between atrial and ventricular rhythms, leading to an elongation of the interval between atrial and ventricular contractions (grade 1 AB block), an increase in the number of atrial contractions compared to the number of ventricular contractions due to blocked conduction of some of the atrial beats (grade 2 AB block) or a complete lack of coordination between atrial and ventricular rhythms (grade 3 AB block). This AB-blockade, as the rhythms Wenckebach due to increase in the interval between contractions of the Atria and ventricles, resulting in the loss of one of the ventricular beats.

Another group is arrhythmias that occur as a result of violations of the formation of impulses. For example, irregular excitation of the Central cells of the ACS leads to such types of disorders as sinus bradycardia (low heart rate), while the frequency of excitations and contractions of the heart can be determined by the activity of the second or third order rhythm drivers, and tachycardia (high rate of contractions) associated with the generation of the heart rate by parasitic high-frequency sources. Arrhythmia due to competition ACS and spurious (ectopic), the leading center emerged from a group of contractile cardiomyocytes, for the reference rate, is called Parasitology. The third group of abnormalities – arrhythmia due to combination of violations.

All types of cardiac arrhythmias can also occur in the absence of anatomically pronounced myocardial changes in practically healthy people, and in this case are called functional, in contrast to pathological disorders that occur with organic changes in the heart (see [3]).

Fibrillation

In a healthy heart, refractoriness provides a normal sequence of propagation of excitation into the heart and electrical stability of the myocardium. Since the area of the myocardium through which the excitation passes become unresponsive for some time, re-entry of the excitation into this area is impossible. Due to this, the counter waves in the myocardium mutually “extinguish” each other, which prevents, in particular, the appearance of unwanted circulation of excitation. However, in the final stage of each excitation cycle, the myocardium becomes inhomogeneous in refractoriness for a short time and loses electrical stability. Stimulus, acting at this time, can lead to serious violations of the normal course of excitation, in particular to the emergence of circulating excitation waves by the mechanism of “re-entry” (re-entry) [3,4].

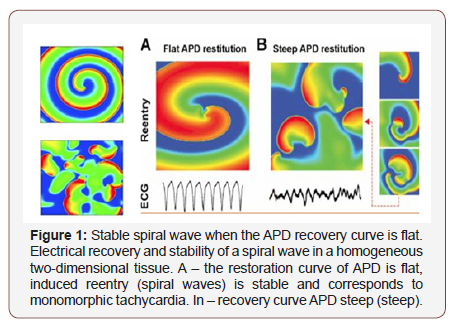
Sharp violations of the normal ratio of excitability and refractoriness can lead to the formation of a large number of reentrant waves in the myocardium, which are spiral waves (Figure 1) on the surface of the heart and complete desynchronization and discoordination of the activity of the myocardial fibers when they begin to excite and contract independently. This condition is called fibrillation and is accompanied by almost complete loss of pumping function of the corresponding part of the heart.

Ventricular fibrillation (VF) is an extreme form of cardiac arrhythmias and the predominant cause of sudden death (due to circulatory arrest) among patients with CVD. Therefore, this pathology is studied particularly intensively. However, there is still no consensus on the mechanism supporting the FF. In one case, it is believed that the LF is due to a single rapidly rotating wave, or the mother rotor, which can be both stationary and wandering, and in interaction with the inhomogeneities of the heart tissue can initiate secondary turbulent activity [5]. In another case, it is assumed that a complex pattern of excitation during LF is formed by multiple re-entrant waves. These two options do not exclude each other, and recent studies have shown that in isolated rabbit hearts, both types of LF can exist [5]. In the dissertation work we adhere to the widespread hypothesis about the presence of multiple rotors during fibrillation in large hearts [6], for example, a person may have about ~ 15 of them.

The theory of dynamic systems describes many processes inherent in active media, including some types of arrhythmias [7]. Since arrhythmias are caused by certain disorders in the heart muscle and, therefore, are pathological conditions, the modeling of such systems is of great practical interest and can bring closer to solving the problem of the possibility of controlling their behavior through external influences. This, in turn, allows us to come close to the problem of soft withdrawal of active systems from the state of developed space–time chaos that characterizes some types of pathologies [8-10].

In this Chapter, we will analyze a discrete oscillating medium model.

Models of active media: application to heart activity

Discrete models of the system of interacting pacemakers: The study of the effect of periodic effects on relaxation oscillations arising in the van der Pol oscillator strongly influenced the development of mathematics in this direction. Early studies of such models demonstrated both bi-stability (the possibility of observing one of the two regimes depending on the initial conditions) and aperiodic dynamics. These and some other results predetermined the development of the theory of maps with complex dynamics [11].

Studies of periodic effects on nonlinear oscillators have shown that multi-stability and aperiodic dynamics can be explained by considering one-dimensional maps of the circle (functions that map the circle to itself, see below) [12]. It was also shown that such maps can demonstrate aperiodic dynamics as a result of a sequence of period doubling bifurcations [13].

A huge number of works were devoted to the study of the dynamics of continuous circle maps both from the point of view of mathematical interest and from the point of view of relation to physical and biological problems [14]. Circle maps can also be discontinuous; bifurcations of these maps are not well investigated. Among the studied discontinuous maps, we can distinguish a piecewise linear monotonically increasing irreversible circle map. Keener [15] considered maps in the case where they have at least one fixed point. Such maps were considered in ergodic theory (see, for example, [16]). The dynamics of irreversible discontinuous maps without fixed points was studied for piecewise linear models in the application to the study of neural networks and analog-todigital converters. But we are primarily interested in applications of circle mapping to the study of cardiac arrhythmias.

Bab (Bub) and glass [17] examined the possible dynamics of a generalized class of discontinuous irreversible maps of a circle without fixed points and applied the results to a mathematical model of ventricular or ventricular parasystole. In [18], attempts were also made to model the parasystole, but the first to use the circle map to study the heart was Acad. V. I. Arnold [19].

Bab (Bub) and glass [17] examined the possible dynamics of a generalized class of discontinuous irreversible maps of a circle without fixed points and applied the results to a mathematical model of ventricular or ventricular parasystole. In [18], attempts were also made to model the parasystole, but the first to use the circle map to study the heart was Acad. V. I. Arnold [19].

Although glass recognized that SAU and ectopic pacemaker, as well as SAU and AVA do not generate pulses independently, and interact in a complex way depending on the electrophysiological properties of cardiac tissue, in his work, the mutual influence of oscillators was not taken into account, even when modeling induced parasystole (sinus pacemaker and ectopic affect each other), not to mention the pure parasystole (when pacemakers do not interact).

In the works of Ikeda [17-18] a piecewise linear pulse model of two-sided interaction of pacemakers based on the circle map is proposed. This model, although taking into account the mutual influence of pulse generation sources and their different nature, was rather primitive, since it used a rather rough approximation of the experimentally obtained phase response curve (PFO) (see below), and it did not allow to predict higher-order arrhythmias (for example, captures of multiplicity 1 ∕ N and N ∕ (N-1)).

Honerkamp [21], trying to investigate the dynamics of a system of coupled oscillators, also used piecewise linear CFO, based on scarce data obtained from the consideration of electrocardiograms. In fact, he operated on some reasoning, but the model has not presented.

Generally speaking, for the mathematical description of the interaction of two pacemakers in the active medium, it is possible to use the known circle map, if this interaction is represented as the effect of some external periodic perturbation (with a constant value of amplitude and frequency) on the nonlinear oscillator [7,22].

Consider three interacting leading centers (pulse oscillators), which can be pacemakers in the heart tissue, build a model of such interaction and investigate its behavior [23].

The principle of constructing a model of three pacemakers

Consider a system of three interacting pacemakers. This case deserves special attention. First, as you know, in the cardiac conduction system, there are three rhythm drivers: SAU – leading pacemaker, AVA and Purkinje fibers – latent pacemakers, which in a normal heart are suppressed by sinus rhythm. However, in case of conduction and excitation disturbances, cardiac pacemakers can affect each other, i.e. the so-called bidirectional communication of pacemakers is realized. Second, in pathology group contractile (excitable) cardiac cells initiates action potentials: you may experience ectopic (abnormal) heart pejjsmeker, which will compete with ACS for the management of heart rhythm. Third, the heart rate can be changed by stimulation of the heart tissue by external impulses. External stimulators can be naturally incorporated into our General model of interacting pacemakers as additional impulse drive oscillators.

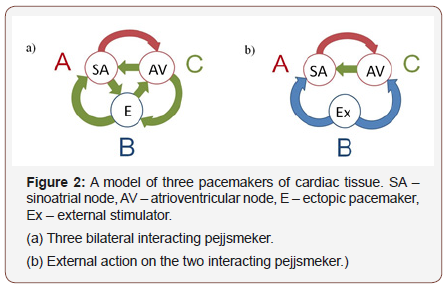
Thus, the representation of the cardiac conduction system as at least three coupled Autonomous oscillators (Figure 2), it is very useful to understand what effect an additional pacemaker has on the system of two bidirectional interacting rhythm drivers (ACS and AVA) discussed above. The study of possible behaviors of more interacting pacemakers is proving to be a very difficult task both analytically and numerically. For example, for a system of five coupled pulse oscillators we will have 25 different functions and 29 different parameters (25 values ε_ij and 4 independent values T_i ∕ T^j). This is due to the fact that in General, cardiac pacemakers have different frequencies (or internal cycle lengths T_i) and different nature. This means that the CFO {f_ij(x, ε_ij)} determining the relationship between a pair of pacemakers have different forms. As mentioned above, for some cardiac pacemakers, CFO were measured by direct experiments on animal cardiomyocytes. Other CFO can be selected using General principles: based on the nature of the nodes or on the basis of collateral measurements.

Applying General model equations (1) for three interacting pacemakers, we obtain the following system:

Response functions Δ_ij have a form Δ_ij(φn^ij,ε_ij) = f_ij(φn^ij,ε_ij)Ti, φn^ij ∈ [0,1], i,j = a,b,c.

Schematically, the system of three bilaterally interacting cardiac pacemakers: ACS, AVA and ectopic pacemaker is shown in Figure 2a.

It is convenient to examine equation (1), introducing the phase difference of the pacemaker.

Submit

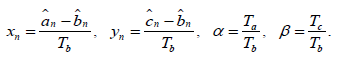
Then, for the phase differences, we obtain a map of the real plane into itself (2):

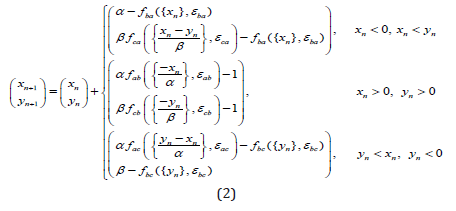
Here we denote {x} as a fractional part of x. the Conditions on the right side (2) divide the plane into three regions corresponding to the active pacemaker (see Fig.3). The mapping (2) has discontinuities on the borders of these areas.

Suppose pejjsmeker B – external stimulus (see Fig.2b). Then the expressions (1), (2) become simpler. Stimulus B acts on pacemakers A and C, but he is not subject to any influence. In this situation, both model (1), (2) can be rewritten as follows:

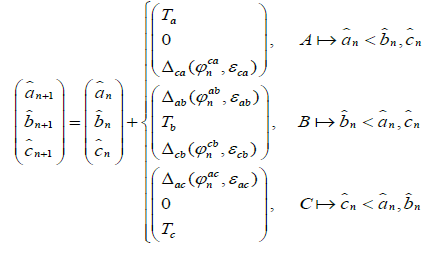
The corresponding expression for phase differences takes the form (3):

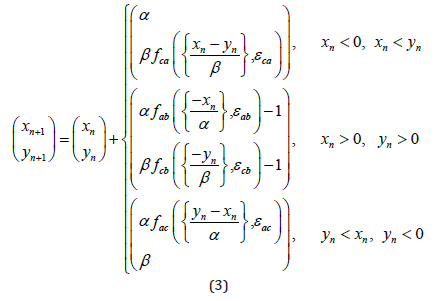
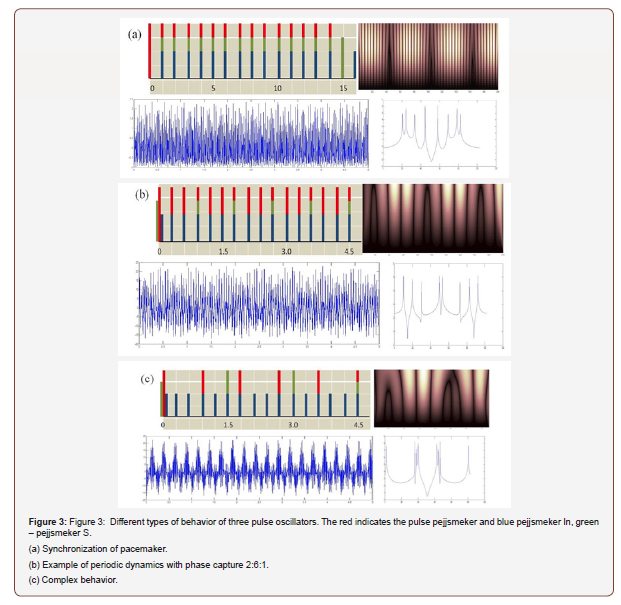
In Figure 3, several examples of phase captures and complex dynamics for the system are shown (1), (2). The RPO is selected in a sinusoidal form, f_ij(x, ε_ij) = ε_ij sin(2πx). These figures show examples of direct modeling of the system (3). The left part of the figure shows some possible phase captures derived from equation (1). The right and bottom parts show the corresponding mappings (3), the time periodicals determine the Fourier and Wavelet spectrum.

Figure 3a shows the synchronization of rhythms with the capture phase of 1:1:1 at:

T_a=1.263, T_b=1.41, T_c=1.098, ε_ab = 0.14, ε_ba = 0.22, ε_ca = 0.31, ε_ac = 0.11, ε_bc = 0.13, ε_cb = 0.12.

Figure 3b shows a periodic dynamic with the capture phase 2:6:1, with:

T_a=1.263, T_b=0.421, T_c=2.098, ε_ab = 0.14, ε_ba = 0.022, ε_ca = 0.31, ε_ac = 0.11, ε_bc = 0.13, ε_cb = 0.012.

T_a=1.2635, T_b=0.4218, T_c=2.0198, ε_ab = 0.14, ε_ba = 0.42, ε_ca = 0.31, ε_ac = 0.11, ε_bc = 0.53, ε_cb = 0.112.

An adequate choice of the force of influence and the period of external stimulation in equations (3) will lead the system from undesirable complex behavior to a normal heart rate. Representation of active media by means of ensembles of coupled excitable or selfoscillating elements is quite a useful method of analysis, because it allows too deeply understand the basic dynamic processes occurring in such environments. As is known, this approach goes back to the Wiener and rosenbluth Model [24], according to which the excitable medium consists of a set of interacting elements in one of three possible States: excitation, refractoriness or rest. Later, such models as limit-cycle oscillators and chaotic maps [25] also began to play an important role not only in a fairly realistic description of active media, but also in understanding the possible behavior of systems that are far from equilibrium.

Since the FF, which lasts only a few minutes, leads to death, emergency intervention is necessary. In an ambulance, a highenergy electrical effect is usually applied to the patient’s chest to restore normal rhythm. The standard defibrillation Protocol includes the use of high voltage electrical shocks (0.01-5 MS/0.1- 10 kV), which return all excitable heart cells to the same state, thus stopping the spiral wave activity.

Usually the first defibrillating shock is set to a certain energy level (200 Joules), and, in case of failure, a second or third shock of the same (or even higher) energy can be applied. The strength of the electric current depends on the location of the electrodes. Modern clinical studies are aimed at improving defibrillation protocols to minimize the percentage of failure and the level of energy used and, therefore, the risk of tissue damage, since high-energy shocks can cause myocardial necrosis or give rise to functional damage, expressed by disorders in the atrioventricular conduction [3].

The method used in medicine is quite effective, most of the knowledge in clinical defibrillation is only practical and empirical [26,27] and there is no full understanding of the mechanisms that stop the activity and a complete consistent theory of cardiac defibrillation.

The use of electrical stimulation to stop fibrillate activity is also used in implantable defibrillators (ID) – devices that are surgically implanted into the bodies of high-risk patients and automatically generate low-power electrical impulses when dangerous activity is fixed. If these impulses do not produce results, the ID begins to produce strong defibrillating shocks. A very important factor in the design of modern ID is to reduce the amplitude of stimulation to avoid painful high-energy shocks and anatomical damage to both the heart and the surrounding tissue, and at the same time maintaining the ability to reliably defibrillate the myocardium. Thus, there is a high need to develop alternative defibrillation methods that would deal with lower voltages.

A study [28] on low-energy defibrillation may be an alternative to conventional ID therapy, as field strengths of 5-10 times lower (or applied energy of 25-100 times) than conventional defibrillating shocks are used to stop recurrent arrhythmias. The idea of the method described in [28] is based on the fact that 80% of patients wearing ID had previous heart attacks, and under certain conditions, re-entry can attach to the scars of non-conductive tissue that arose due to a heart attack (the so-called anatomical re-entry). However, not all high-risk patients had previous heart attacks. Therefore, arising in the hearts of a large number of patient’s re-entrant arrhythmias are usually associated with functional re-enter (freely drifting rotating waves) and require other methods of elimination.

Currently, there are two qualitatively different approaches to this problem. The first of them provides removal of system from chaotic on a regular mode by means of the external disturbances realized without feedback (suppression of chaos), i.e. it does not consider its current state. A qualitatively different method is implemented through corrective action and thus involves feedback as a necessary component of the dynamic system (chaos control) [29].

Theoretical studies confirm that low-energy defibrillation protocols are possible when using the dynamic properties of reentrant waves under electric force, known as resonant drift with feedback [30]. It is assumed that low-amplitude shocks (by an order of magnitude lower than those used in classical defibrillation) are sufficient to displace (and subsequent annihilation) functional reentrant sources on the non-excitable boundaries of cardiac tissue. If the frequency of exposure is equal to the resonance frequency, it can move the rotating waves, step by step, inside the heart muscle in the desired direction and, eventually, eliminate them. However, the main problem in the practical use of resonance drift is to change the resonance frequency when the position of the re-entrant wave changes, in particular near the boundaries. Thus, the change in the frequency of exposure should be determined by the events caused by the exposure itself, i.e. feedback. In a real situation fibrillating activity associated with multiple rotating waves, the destruction of all of the waves can take too much time, because the recording electrode in each moment of time records the activity of only one rotating wave. Therefore, it determines the frequency of a single wave and causes it to drift (or at best several waves), and other re - entrant waves have to wait “their turn”, while the complex activity develops further, which can cause the emergence of new re - entrants.

Parametric effects of feedback were used [31] to correct less dangerous arrhythmias (AV - block, parasitology).

For the development of the analytical approach to the parametric control let us consider a map:

T_a: M → M, T_a: x → f(x,a), where a ∈ A, f = {f₁,...., f_n}, x = {x₁,...., x_n}.

We define the perturbation G acting on the set of parameters A, G : A → A as, G_a : a → g(a), (a, g(a)) ∈ A.

Then the resulting perturbed map can be written as

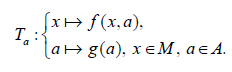
The period P of any cycle of the periodically perturbed map is determined from the relation: P = τk, where τ is the perturbation period and k is a positive integer [32]. It is shown that the whole dynamics of the perturbed map will be given by a set of Autonomous maps that act independently of each other and are connected only by initial conditions. This is true for any set of admissible values A of the parameter a of a dynamical system with periodic perturbation [33].

With regard to fibrillation, the only application of parametric action is the formulation of drug therapies that modify ionic currents in order, for example, to prevent alternations (alternation of the duration of the action potential from beating to beating), which are presumably one of the causes of the decay of rotating waves into a set of re-entry’s [34].

Studies in the field of the theory of active media offer new opportunities for electrical defibrillation: the amplitude of external action can be significantly reduced, and the turbulent regime in excitable systems can be stabilized by a sufficiently weak periodic external force applied globally [35] or locally [36]. Using this method, it is possible not only to suppress the space-time chaos and stabilize the dynamics of the environment, but also, in some cases, to restore a normal heart rate, because after stabilization the environment goes to a spatially homogeneous stable state, where there is a leading center (ACS).

None.

No conflict of interest.

1. Wagner CD, Persson PB (1998) Chaos in the cardiovascular system: An update. Cardiovasc Res 40(2): 257-264.
2. Goldberger AL (1990) Nonlinear dynamics, fractals and chaos: Applications to cardiac electrophysiology. Ann Biomed Eng 18(2): 195-198.
3. (1985) Cardiac Electrophysiology and Arrhythmias. Eds. Zipes DP, Jalife J Orlando, Grune and Stratton.
4. Winfree AT (2000) The Geometry of Biological Time. 2^nd New York: Springer-Verlag.
5. Clayton R, Zhuchkova E, Panfilov A (2006) Phase singularities and filaments: Simplifying complexity in computational models of ventricular fibrillation. Prog Biophys. Mol Biol 90(1-3): 378-398.
6. Jalife J, Gray RA, Morley GE, Davidenko JM (1998) Self-organization and the dynamical nature of ventricular fibrillation. Chaos 8(1): 79-93.
7. (2003) Nonlinear Dynamics in Physiology and Medicine. Eds. Beuter A, Glass L, Mackey MC, Titcombe MS, New York: Springer-Verlag, Inc.
8. Witkowski FX, Penkoske PA, Plonsey R, Kaplan DT, Spano ML, et al. (1995) Development of a nonlinearly deterministic signal generator for real time chaos control testing. Eng in Medicine and Biology Soc. IEEE 17^th Ann Conf 1: 287-288.
9. Brandt ME, Guanrong Chen (1996) Feedback control of a quadratic map model of cardiac chaos. Int J Bifurcation and Chaos 6(4): 715-723.
10. Garfinkel A, Spano ML, Ditto WL (1992) Controlling cardiac chaos. Science 257(5074): 1230-1235.
11. Smale S (1980) The Mathematics of Time. New York: Springer, pp. 147.
12. Levi M (1981) Qualitative analysis of the periodically forced relaxation oscillations. Memoirs Amer Math Soc 32: 1-147.
13. Guckenheimer J, Holmes P (1983) Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. New-York: Springer-Verlag.
14. Bak P (1986) The devil’s staircase. Physics Today 39(12): 38-45.
15. Keener JP (1980) Chaotic behavior in piecewise continuous difference equations. Trans Am Math Soc 261: 589-604.
16. Lasota A, Yorke JA (1973) On the existence of invariant measures for piecewise monotonic transformations. Trans Am Math Soc 186: 481-488.
17. Bub G, Glass L (1995) Bifurcations in a discontinuous circle map. A theory for chaotic cardiac arrhythmia. Int J Bifurcation and Chaos 5: 359-371.
18. Courtemanche M, Glass L, Belair J, Scagliotti D, Gordon D (1989) A circle map in a human heart. Physica D 40(3): 299-310.
19. Arnold VI (1991) Cardiac arrhythmias and circle mappings. Izrail M Gelfand: Collected Papers. Eds. Gindikin SG, Guillemin VW, Kirillov AA, Kostant B, Sternberg S Berlin: Springer-Verlag. P3. Reprinted in Chaos 1: 20-24.
20. Glass L (1991) Cardiac arrhythmias and circle maps – A classical problem. Chaos 1(1): 13-19.
21. Honerkamp J (1983) The heart as a system of coupled nonlinear oscillators. J Math Biol 18(1): 69-88.
22. Glass L, Guevara MR, Shrier A, Perez R (1983) Bifurcation and chaos in a periodic stimulated oscillator. Physica D 7(1-3): 89-101.
23. Loskutov A, Rybalko S, Zhuchkova E (2004) A model of cardiac tissue as a conductive system with interacting pacemakers and refractory time. Int J Bifurcation and Chaos 14: 2457-2466.
24. Wiener N, Rosenblueth A (1946) The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle. Arch Inst Cardiologia de Mexico 16(3): 205-265.
25. Kaneko K (1990) Clustering, coding, switching, hierarchical ordering, and control in a network of chaotic elements. Physica D 41(2): 137-172.
26. Krinsky VI (1966) Spread of excitation in an inhomogeneous medium: State similar to cardiac fibrillation. Biophysics 11: 676-683.
27. Rodriguez B, Eason JC, Trayanova N (2006) Differences between left and right ventricular anatomy determine the types of reentrant circuits induced by an external electric shock. A rabbit heart simulation study. Progr Biophys Mol Biol 90(1-3): 399-413.
28. Takagi S, Pumir A, Pazo D, Efimov I, Nikolski V, et al. (2004) Unpinning and removal of a rotating wave in cardiac muscle. Phys Rev Lett 93(5): 058101-1–058101-4.
29. Ott E, Grebogi C, Yorke JA (1990) Controlling chaos. Phys Rev Lett 64(11): 1196-1199.
30. Biktashev VN (1997) Control of re-entrant vortices by electrical stimulation. Computational Biology of the Heart. Eds. Panfilov AV and Holden AV Chichester: Wiley, Pp. 137-170.
31. Alonso S, Sagues F, Mikhailov AS (2003) Timing Winfree turbulence of scroll waves in excitable media. Science 299: 1722-1725.
32. Loskutov A, Shishmarev AI (1994) Control of dynamical systems behavior by parametric perturbations: An analytic approach. Chaos 4(2): 351-355.
33. Loskutov A, Rybalko SD (1994) Parametric perturbations and suppression of chaos in n-dimensional maps. Preprint ICTP, Trieste, Italy.
34. Allexandre D, Otani NF (2004) Preventing alternans-induced spiral wave breakup in cardiac tissue: An ion-channel-based approach. Phys Rev E 70 (6 Pt 1): 06190-3–06190-6.
35. Gray RA (2002) Termination of spiral wave breakup in a Fitzhugh-Nagumo model via short and long duration stimuli. Chaos 12(3): 941-951.
36. Zhang H, Cao Z, Wu NJ, Ying HP, Hu G (2005) Suppress Winfree turbulence by local forcing excitable systems. Phys Rev Lett 94(18): 18830-1–18830-4.