Determination Of The Relief Complexity Factora

Determination of relief complexity degree is the most important factor for decision of implementation of different engineering tasks and at the same time the least studied. It shall be noted that the degree of complexity or roughness has a word description as a flat or undulating terrain, rugged topography, smooth relief, etc. and has not numerical characteristics, that, obviously, presents a basic difficulty of their practical use.

In writings [1] there is a description of determination of geometrical model TS complexity degree, where accumulated absolute intrinsic and extrinsic curvatures of crests determine the degree of model complexity. There is also a definition that the simplest surface – plane – has complexity degree equal to “0” irrespective of number of considered crests.

In the engineering practice there is not a unified methodology of determination of relief complexity or roughness degree. In writings [2] there is an approach to this task by methods of probability theory and mathematical statistics based on data of topographic location plan. The work is based on ratio of isolines concentration to dm2 and takes into consideration indications of water parting lines, baffle-walls thalwegs, bases, etc. This approach is not applicable to DMR (Digital Model of Relief) as modern DMR is based on regular or irregular data grid. Consequently, the relief complexity degree is directly related to these data and may be determined by correlation of these data.

If surface may be considered as aggregate of consecutive positions of line moving in space according to definite law [3,4,5], let us determine some degree of complexity for plane curve as interpolation of regular grid points by the least distance along X or Y is a plane curve.

Let us consider the complexity of line given by minimal quantity of points:

Two points of line simply determine the right line for which degree of curvature will be “0”.

Three points on the plane may lie either on the line, or outside the direct trajectory. Thus, the degree of curvature –complexity of line may be defined through location of three points on the plane.

Further, let us consider a surface with minimum number of points. Three points in the space shall monotypically determine the plane, for which is determined the degree of complexity equal to «0». Four points in the space may determine either a plane, or skew plane, but cannot determine closed convexity or concavity. Intersection of two or three planes given on the rectangular regular mesokurtic form a truncated unclosed vertex. Thus, for rectangular regular mesokurtic is fair the consideration of four intercrossing planes, which shall determine in particular case, both the plane, and the character of convexity or concavity of the considered surface (Figure 1).

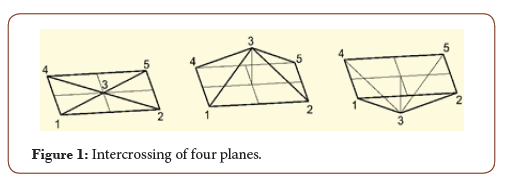
On the rectangular regular mesokurtic, the considered four planes may be given by five points. By connecting of intermediate four points it is possible to increase the number of planes to eight. Hence, nine points of regular mesokurtic (3×3) form a square of four cells (quadrants).

Let us establish some correlation between nine terms of matrix by the finite difference method:

• Let us take an absolute value of the sum of row elements difference and differentiate:

where ΔX is an interval of rectangular regular mesokurtic along the rows.

• Let us take an absolute value of the sum of column element difference and differentiate:

where ΔY is an interval of rectangular regular mesokurtic along the columns.

• Let us summarize the absolute value of diagonal elements difference and differentiate in the same manner:

Equations (2–4) shall be summarized and so we obtain some value known as ξ for the square of the surface:

This equation satisfies to the definition of degree of complexity of the surface ξ=0 and gives us different values, if the considered surface is not a plane.

The degree of complexity of irregular (topographic) surface may be also defined by considering the TS as a population of adjacent regular surfaces, and the sum of degree of complexity of squares gives a rough idea of the degree of complexity of TS in total. Thus, the degree of complexity of the whole section of the surface will be:

The numerical value of complexity of project surface gives an option possibility of project realization, economical accounting of energy resources, bringing in some factors of complexity of realization of the project etc.

On leave from Total Quality Mangement, Gedeon Richter Plc.

No conflict of interest.