 Research Article
Research Article
Adaptive Sliding Mode Guidance Law Considering Input Saturation and Autopilot Lag
Jun Guan1, 2* and Wenjun Yi2
1School of Automation, Nanjing University of Science & Technology, China
2National Key Laboratory of Transient Physics, Nanjing University of Science & Technology, China
Jun Guan, School of Automation, National Key Laboratory of Transient Physics, Nanjing University of Science & Technology, China.
Received Date: July 05, 2019; Published Date: July 11, 2019
Abstract
In this article, a guidance law is developed using the sliding mode control theory. The law will have a good guidance performance when intercepting a maneuvering target under considering the input saturation and autopilot lag. Regarding the target acceleration as unknown bounded external disturbance, the adaptive control is designed to estimate the upper bound of the disturbance in such a way that it is not required to be known in advance. A sliding mode estimator is also presented to estimate the line-of-sight angle rate which the guidance law is required. According to the Lyapunov theory, the guidance law can be converted to zero is proved. Several simulations include 100 Monte-Carlo are made to valid the effectiveness of proposed guidance law.
Keywords:Guidance law; Adaptive sliding mode; Missile; Input saturation
Introduction
Modern missile interceptors are designed to engage and destroy a large range of highly maneuverable targets. The major requirement for such defensive missiles, designed to negate these threats, is improved interception performance, i.e., attaining small miss distance, in order to ensure destruction of the target. Possible solutions to deal with this challenge are to develop advanced sensors, to build a more energetic missile and/or to install a more lethal warhead. These approaches are very often complicated and expensive. An alternative method is to improve the guidance and control systems of the missile so they will be able to achieve the required interception accuracy without changing its platform. Obviously, the latter is preferable, because it allows not only to build new missiles, but also to modernize the old ones simply by updating their guidance and control algorithms with sophisticated software.
In the missile industry it is common to design the guidance and control subsystems separately. This approach, frequently, where the inner-loop autopilots are designed to follow the acceleration commands generated by the outer-loop guidance algorithms, is valid. In this paper, the works are only focus on how to design the outer loop.
The issue of achieving an excellent intercepting performance has been addressed in several contributions in the missile guidance literature. A technique that has been commonly applied to derive such laws is to linearize the kinematics-based engagement dynamics. One of the initial efforts in this direction is [1], where a sub-optional guidance law is designed for a ballistic reentry vehicle to intercept a non-maneuvering target. Because the guidance law is derived without any input constraints, its performance is expected to degrade in the presence of input constraints. A guidance law which considering a saturation on the terminal missile lateral acceleration is presented in [2]. This guidance law developed to intercept a stationary target. A time-optimal guidance law that aims to minimize the flight time to intercept stationary targets in the presence of bounded lateral acceleration is proposed in [3].
In [4], the guidance law has been derived as the solution to a nonlinear regulator problem using the state dependent Ricatti equation technique. In [5,6], two-stage PN guidance laws with different navigation constants to intercept stationary nonmaneuvering targets are designed using nonlinear engagement dynamics. Another guidance law, also based on nonlinear engagement dynamics but adopting a computational approach, defined by the particle-swarm-optimization algorithm, is derived in [7]. A game-based guidance law is presented in [8], the linear engagement dynamics is used. Other guidance design methods were also applied to solve this problem, covering predictive control methodology [9], geometric control theory [10], feedback linearization [11], nonlinear H∞ control theory [12], sliding mode control [13,14], to name just a few.
In this paper, guidance laws are designed using nonlinear engagement dynamics to intercept maneuvering targets based on the algorithm of Sliding mode Control. Input saturation and autopilot lag are considered. Besides, an estimator is designed in this paper to estimate the Line-of-Sight (LOS) angle rate.
The paper is organized as follows. In Sec 2, the problem formulation is given. In Sec.3 the guidance law is designed. In Sec.4, the LOS angle rate estimator is given. In Sec.5, simulation results are presented to validate the performance of the proposed guidance law. Finally, in Sec.6, conclusions are offered.
Problems Formulation
The target interception problem is essentially a threedimensional problem in a practical engagement scenario. However, to demonstrate the efficacy of the sliding mode-based guidance scheme, the problem is addressed in a planar scenario. As in other guidance laws, the planar guidance laws can be used in a three-dimensional situation by appropriate decomposition of the engagement into two orthogonal planes. Consider a planar engagement between an interceptor and a target as shown in Figure1. This figure depicts the planar end-game interception geometry, where O − XI −YI is a Cartesian inertial reference system, and the missile and the target are denoted by the subscripts M and T , respectively. The kinematics of the interception terminal phase is expressed in the polar coordinate system (r, q) attached to the missile. Here represents the range between the interceptor and the target and represents the angle between the current LOS and the reference direction parallel to the I X axis. Neglecting gravity, the depicted kinematics can be expressed by
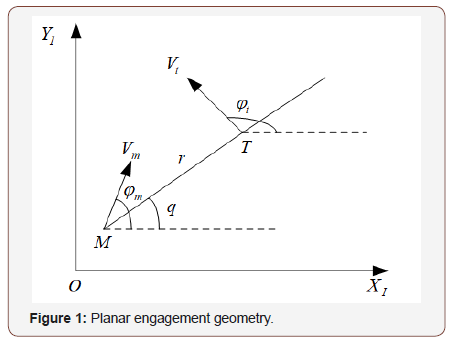
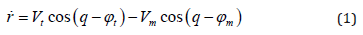
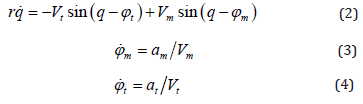
where 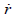 is the relative speed along LOS, or the closing speed?
ϕm and ϕt
are the missile and the target flight angle, respectively.
Vm is the missile speed and is the target speed, are the normal
acceleration of the missile and the target, respectively?
is the relative speed along LOS, or the closing speed?
ϕm and ϕt
are the missile and the target flight angle, respectively.
Vm is the missile speed and is the target speed, are the normal
acceleration of the missile and the target, respectively? 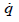 is the
LOS angle rate.
is the
LOS angle rate.
Derivative with respect to equation (1) and (2), are given by
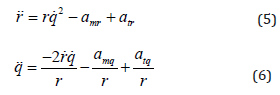
where, are the missile and target acceleration along the LOS, respectively. amq , atq the missile and target acceleration normal to the LOS, respectively. The expressions are given by
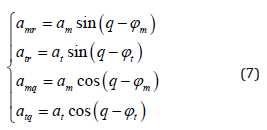
In this study the missile autopilot lag is considered. The autopilot dynamic property is described with first-order differential equation, given by
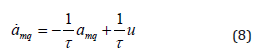
where, τ is the time constant of the missile autopilot, u is the guidance command providing to the missile autopilot.
Previous works show that 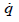 →0makes the interceptor
impacting the target. In this study, a guidance law is designed
to make the miss distance as small as possible. In other words,
the works designed a guidance command to make asymptotic
convergent to zero.
→0makes the interceptor
impacting the target. In this study, a guidance law is designed
to make the miss distance as small as possible. In other words,
the works designed a guidance command to make asymptotic
convergent to zero.
Defining state variables 1 x= 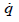 and 2x =
and 2x = 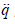 , equation (6) can be
rewritten as
, equation (6) can be
rewritten as
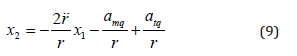
Obviously, with equation (9), we get
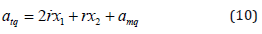
Differentiating equation (9) with respect to time, we obtain
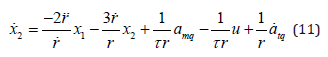
Combine equation (9) and (11), the state equation of guidance loop considering autopilot dynamic behavior can be given by
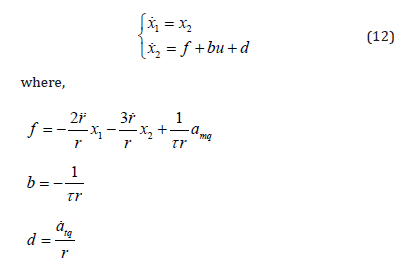
‘d’ be an exterior disturbance.
Guidance Law Design
Considering the saturation condition of input command of missile autopilot, the state equation of guidance loop can be rewritten as the following form
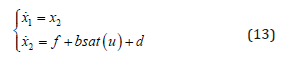
where, sat (⋅) is a saturation function by the definition with
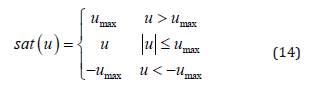
where, umax is the maximum value of the input command which to be seen as a constant number in this paper.
For equation (13), in this study, the aim is designing an input command to make the state variables x1 and x2 asymptotic converging to zero. To be design a sliding mode guidance law, the first step is how to design a sliding mode surface. Herein, the following linear sliding surface is selected in this paper.

where, k > 0 is a constant value.
In order to the state variable of guidance system converging to zero more quickly and obtaining a better guidance performance, a reaching law is used in the study. Given by
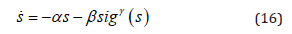
where,
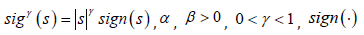 is sign
function.
is sign
function.
A lemma and an assumption are given first, then proving the theorem used in this study.
Lemma 1 For the guidance loop state function considering
the input saturation, if sliding surface s satisfy 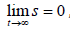 ,then
,then 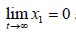 and
and 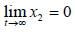 also be satisfied.
also be satisfied.
Assumption 1 is regard as the total disturbance, which is a
bounded value in the practical guidance process. It also be satisfied
the condition of 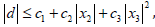 c1 , c2 and c3 are unknown
positive constant value.
c1 , c2 and c3 are unknown
positive constant value.
Theorem 1 For the guidance system (13), considering input saturation and autopilot lag, if Assumption 1 holds, the sliding surface is selected as equation (15), and the designed guidance law as equation (17) shows, the sliding surface will asymptotic converged to zero. And then the state variable 1 x and 2 x as the same converged to zero.
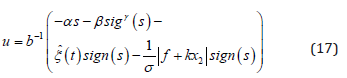
where, 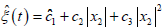 and the adaptive law is
designed as follow
and the adaptive law is
designed as follow
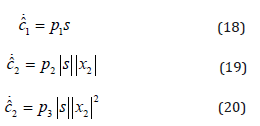
where, p1, p2 , p30, η > 0
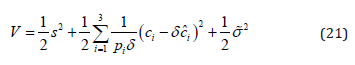
where, 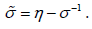 Differentiating V , we can obtain
Differentiating V , we can obtain
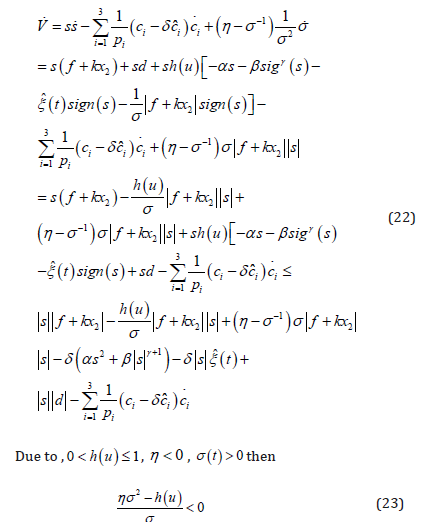
According to equation (23), following formula holds.
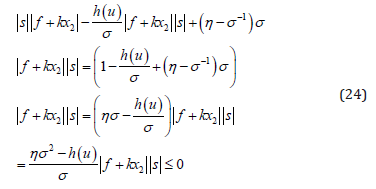
Furthermore, by the equation (22) and (24), we can obtain
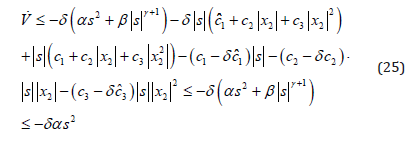
From equation (25), known that 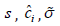 are all have bounded
limit. Defining ζ =δαs2 , and putting equation (25) on to
integration, gives
are all have bounded
limit. Defining ζ =δαs2 , and putting equation (25) on to
integration, gives
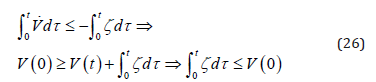
If t → ∞ , then 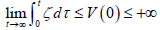 By Barbalat theorem,
By Barbalat theorem,
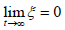 = is obtained. And then is also obtained. Lastly, based on the
Lemma 1,
= is obtained. And then is also obtained. Lastly, based on the
Lemma 1,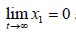 and
and 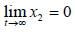 are deduced.
are deduced.
Because the sign function used in the guidance law in equation (17) easily generate chattering phenomena. In this study, we use continues saturation function replacing sign function. The expression of saturation function is as follows
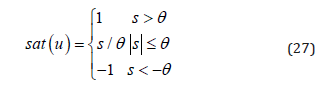
where,θ is a small positive constant.
Instead saturation function of sign function, the improved guidance law can be written as
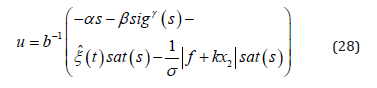
LOS Rate Measurement and Estimation
The guidance system presented in (12) require the knowledge
of the LOS angle rate 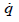 . In realistic flight control system, these
variables cannot be measured directly and therefore must be
estimated. Many estimation methods were used in previous
works, such as Kalman Filter [15],α −β Filter [16], divided
difference filters [17]. In this study, we incorporate a relatively
simple estimator called sliding mode observer / differentiator to
demonstrate the estimation effect of the interception accuracy.
. In realistic flight control system, these
variables cannot be measured directly and therefore must be
estimated. Many estimation methods were used in previous
works, such as Kalman Filter [15],α −β Filter [16], divided
difference filters [17]. In this study, we incorporate a relatively
simple estimator called sliding mode observer / differentiator to
demonstrate the estimation effect of the interception accuracy.
The first proposed SMOD scheme is known as the super twisting
algorithm. This algorithm can reconstruct a signal 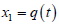 and its
derivative
and its
derivative 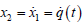 from noisy measurements of q (t ) , provided
its second derivative of is bounded. Assuming the bound
from noisy measurements of q (t ) , provided
its second derivative of is bounded. Assuming the bound 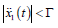 for all t is known, the SMOD is given by
for all t is known, the SMOD is given by
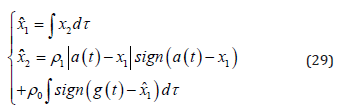
If the parameters ρ0
and ρ1
are chosen as 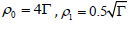 , then
, then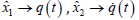 is received in a finite time. In our study, we use a modified SMOD to do our works. The modified scheme is
is received in a finite time. In our study, we use a modified SMOD to do our works. The modified scheme is
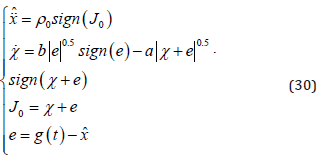
When on the sliding surface J0 = 0 , the estimator error dynamics is governed by
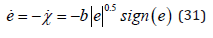
which ensures a finite time convergence to the origin 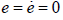 .
.
The LOS angle rate and its derivative are estimated from noisy
measurement of the LOS angle. The SMOD is implemented as a
“differentiator” of the LOS angle, providing smoothed estimates
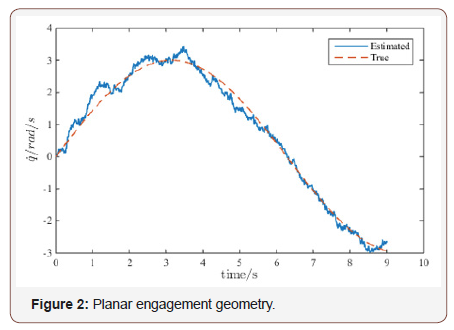
of q and 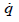 . Figure 2 give a simulated result of estimate
. Figure 2 give a simulated result of estimate 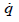 . The
simulation parameters of this estimator is a = 120 , b = 0.2 and
ρ0 = 2800 . Though the estimator result has some difference from
the true value, it always satisfies the accuracy requirement in
engineering.
. The
simulation parameters of this estimator is a = 120 , b = 0.2 and
ρ0 = 2800 . Though the estimator result has some difference from
the true value, it always satisfies the accuracy requirement in
engineering.
Numerical Simulations
The interception performance is evaluated in this section using nonlinear simulation. The following parameters are used in the simulation: initial missile position (0,0) , initial target position (3000, 4000) , initial missile flight angle ϕm(0) = 30deg , initial target flight angel ϕt(0)=-20deg missile velocity Vm=500m/s, , target velocity Vt=200m/s, maximum guidance command , missile autopilot time constant.
The parameters of designed guidance law are: α = 1, β = 1, γ = 0.8 , k = 8 , p1 = 0.1, p2 = 0.1, p3 = 0.1 ,θ = 0.002.In order to validate the performance of designed guidance law, two types of different target acceleration are chosen in this study. Given by
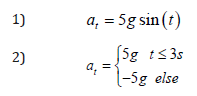
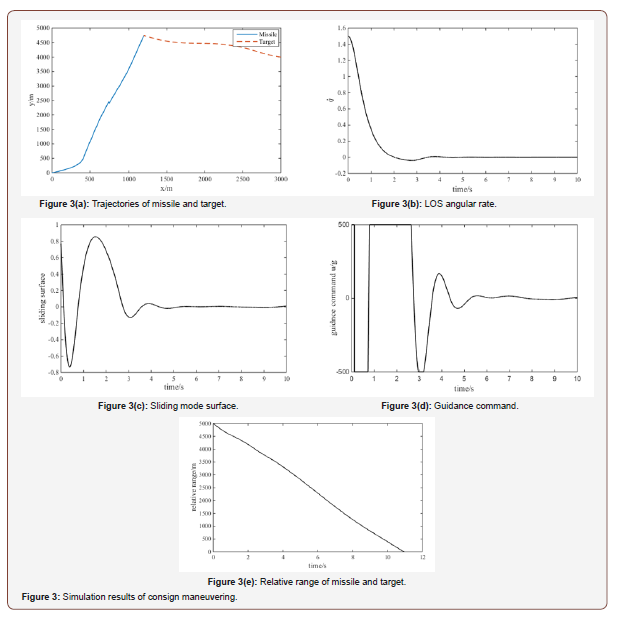
Figures 3 & 4 clearly depict the performance of designed
guidance law. Figures 3(a) & 4(a) shows that the interceptor has a
small miss distance, the guidance accuracy completely satisfied the
requirement. We will also give a more detailed analyze about the
miss distance of designed guidance law in the end of this section.
With the two type of target maneuvering property, Figures 3(b-c)
& 4(b-c) indicate that LOS angular rate and sliding mode surface
are convergent to zero, the interceptor will impact the target at
suitable time. Figures 3(d) & 4(d) denote the input command of
the guidance system. When at the beginning of the guidance system
works, input command saturation occurred, and then falloff with 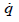 and s convergence to zero. Figures 3(e) & 4(e) shows the relative
distance between missile and target, it means that missile and
target are closer and closer with time increase.
and s convergence to zero. Figures 3(e) & 4(e) shows the relative
distance between missile and target, it means that missile and
target are closer and closer with time increase.
For give a detailed analysis of the miss distance, the method
of Monte-Carlo simulation is used here. The simulation considers
the measurement noise of and estimated error of 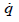 . The noise of
relative velocity includes a random variation of ±10% around its
nominal value. 100 Monte-Carlo runs. Results of the simulation are
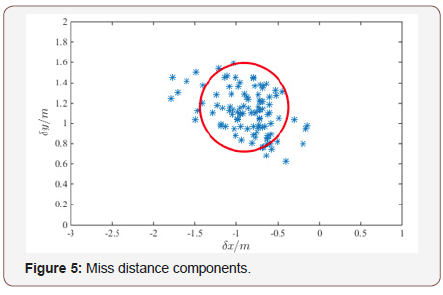
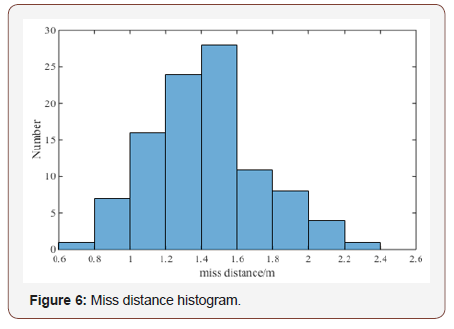
depicted in Figures 5 & 6.
. The noise of
relative velocity includes a random variation of ±10% around its
nominal value. 100 Monte-Carlo runs. Results of the simulation are
depicted in Figures 5 & 6.
Figure 5 is the miss distance components in and axis. Figure 6 is a histogram of the simulation result. The above two figures show that the designed guidance law in this study have an excellent performance. From the result we known that the average miss distance of 100 Monte-Carlo runs is about 1.4 meters. This quality indicator can satisfy the requirement of engineering application.
Conclusion
This article developed an adaptive guidance law considering the input saturation and autopilot lag to intercept a maneuvering target. The detailed process for proving the command input is given. Sliding mode estimator is used to estimate the LOS angle rate. Simulations indicate that the proposed guidance law have a very high performance. Also, the Monte-Carlo results shows the interceptor has a small miss distance.
Funding
This work was supported by the National Natural Science Fund Project of China (No.11472136).
Acknowledgement
None.
Conflict of Interest
The authors declare that there is no conflict of interests regarding the publication of the paper..
References
- Kim M, Grider KV (1973) Terminal Guidance for Impact Attitude Angle Constrained Flight Trajectories. IEEE Transactions on Aerospace and Electronical Systems 9(6): 852-859.
- Lee Y, Ryoo C, Kim E (2003) Optical Guidance with Constraints on Impact Angle and Terminal Acceleration. AIAA Guidance Navigation and Control Conference and Exhibit, Austin, TX, AIAA paper 2003-5795.
- Song TL, Shin SJ (1999) Time-Optimal Impact Angle Control for Vertical Plane Engagements. IEEE Transactions on Aerospace and Electronic Systems 35(2): 738 - 742.
- Ratnoo A, Ghose D (2009) State-Dependent Riccati-Equation-Based Guidance Law for Impact Angle Constrained Trajectories. Journal of Guidance Control and Dynamics 32(1): 320-326.
- Ratnoo A, Ghose D (2008) Impact Angle Constraint Interceptor of stationary Targets. Journal of Guidance Navigation and Dynamics 31(6): 1816-1821.
- Ratnoo A, Ghose D (2010) Impact Angle Constrained Guidance Against Nonstationary No Maneuvering Targets. Journal of Guidance Control and Dynamics 33(1): 269-275.
- Sang D, Min BM, Tahk MJ (2007) Impact Angle Control Guidance Law Using Lyapunov Function and PSO Method. SICE Annual Conference 2007, IEEE Publ, Piscataway, Japan, pp. 253-2257.
- Shaferman V, Shima T (2008) Linear Quadratic Guidance Laws for Imposing a Terminal Intercept Angle. Journal of Guidance Control and Dynamics 31(5): 1400-1412.
- Thlole SE, Banavar RN (1998) Proportional navigation through predictive control. Journal of Guidance Control and Dynamics 21(6) :1004-1006.
- Bezick S, Rusnak I, Gray WS (1995) Guidance of homing missile via nonlinear geometric-control method. Journal of Guidance, Control and Dynamics 18(3): 277-288.
- Menon PK, Sweriduk GD, Ohlmeyer RJ (2003) Optimal fixed-interval integrated guidance-control law for hit-to-kill missiles. AIAA guidance navigation and control conference and exhibit, Austin, TX, Reston.
- Yang CD, Chen HY (1998) Nonlinear H robust guidance law for homing missiles. Journal of Control Dynamics 21(6): 882-890.
- Alexander Z, Moshe I (2011) Effect of estimation on the performance of an integrated missile guidance and control system. IEEE Transactions on Aerospace and Electronical Systems 47(4): 2690-2708.
- Song JH, Song SM (2015) Adaptive sliding mode guidance law with input constraints and autopilot lag. Journal of Chinese Inertial Technology 23(3): 339-344.
- Vaddi SS, Menon PK, Ohlmeyer EJ (2007) Target state estimation fore integrated guidance-control of missiles. AIAA Guidance Navigation and Control Conference and Exhibit, Hilton Head, SC.
- Sarkar AK (2007) Nonlinear state estimator base on realistic seeker measurements for closed loop applications. International Conference on Advances in Control and Optimization of Dynamical Systems, Bangalore, India.
- Masataka H, Tetsuya K, Iwao S (2002) Maneuver target tracking with an acceleration estimator using target past positions. Electronical and Communication in Japan 85(12): 29-37.
-
Jun Gua, Wenjun Yi. Adaptive Sliding Mode Guidance Law Considering Input Saturation and Autopilot Lag. Glob J Eng Sci. 2(5): 2019. GJES.MS.ID.000550.
-
Guidance law, Adaptive sliding mode, Missile, Input saturation
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






