 Research Article
Research Article
A 3D Star-Shaped zero Poisson’s Ratio Honeycomb with Cubic Symmetry
Zhang Wenzhi*, Jie Dianmin, Li Zhiwei and Song Nanxin
School of Civil Engineering and Architecture, Wuyi University, Jiangmen 529020, P.R. China
Zhang Wenzhi, School of Civil Engineering and Architecture, Wuyi University, Jiangmen 529020, P.R. China.
Received Date: February 25, 2021; Published Date: March 08, 2021
Abstract
A three-dimensional (3D) star-shaped zero Poisson’s ratio (ZPR) honeycomb with cubic symmetry is proposed in this paper based on a twodimensional (2D) star-shaped ZPR honeycomb. Based on the Timoshenko beam theory and the energy method, the analytical formulas for the equivalent Young’s modulus and the specific stiffness of the new honeycomb are obtained, which are verified by the numerical analysis and the experiments. The results show that the proposed new honeycomb has the ZPR effect in all three principal directions with the same equivalent Young’s modulus. With this excellent property, the novel honeycomb is of good application prospect in some important fields, such as anti-collision facilities and wing morphing. In addition, the influence of the geometric parameters on this new honeycomb’s elastic performance is further studied. The results show that the new honeycomb’s elastic performance can be significantly improved by increasing either the thin struts’ slant angle or the ratio of width to height of the thin struts. This study provides a new idea for the design of 3D ZPR honeycombs.
Keywords: Zero Poisson’s ratio (ZPR); Equivalent parameters; Timoshenko beam theory; Three dimensional (3D); Star-shaped honeycomb
Introduction
Metamaterial is a kind of artificial composite material or structure with extraordinary physical properties [1]. As one type of Metamaterial, the zero Poisson’s ratio (ZPR) metamaterial and the negative Poisson’s ratio (NPR) metamaterial are of abnormal Poisson’s ratio effect [2-3]. Due to their unique properties in energy absorption and coaxial curvature, these materials are playing an increasingly important role in some important fields such as aerospace, transportation and biomedicine.
Research on the NPR honeycombs is becoming abundant [4-5], while research on the ZPR honeycombs is relatively lagging. Most research on the ZPR honeycombs focuses on the 2D honeycombs, such as the semi re-entrant (SRE) honeycomb [6-9], accordion honeycomb [9-11], star-shaped ZPR honeycomb [12], reversed semi re-entrant (RSRE) honeycomb [13] and mixed cruciform honeycomb [14-16]. Some other research focuses on forming novel 2D ZPR honeycombs by combining multiple structures [17], adding structural thin struts [18] or changing the shape of structural thin struts [19-23].
Compared with 2D honeycombs, 3D honeycombs have the potential to perform the same equivalent elastic properties in all three principal directions, which has been demonstrated by some NPR honeycombs (e.g., [24-29]). However, there are not many honeycombs with ZPR effect in all three principal directions, and it is even rarer for 3D ZPR honeycombs to exhibit the same equivalent Young’s modulus in all three principal directions. Wang et al. [30] extended the 2D SRE honeycomb, RSRE honeycomb and their hybrid cellular to 3D, but only the 3D RSRE honeycomb showed ZPR effect in three principal directions. Chen et al. [31] designed a 3D honeycomb which shows NPR effect in two principal directions and ZPR effect in another principal direction. Yang and Ma [32-33] proposed two kinds of 2D U-shaped honeycombs, which were expanded into a series of 3D ZPR honeycombs, but the mechanical properties are mainly reflected in one principal direction.
This paper proposes a 3D star shaped ZPR honeycomb with the same equivalent elastic properties in three principal directions. The equivalent elastic properties of this novel honeycomb are analyzed in the elastic range, and the relation between its geometric parameters and equivalent elastic properties is discussed.
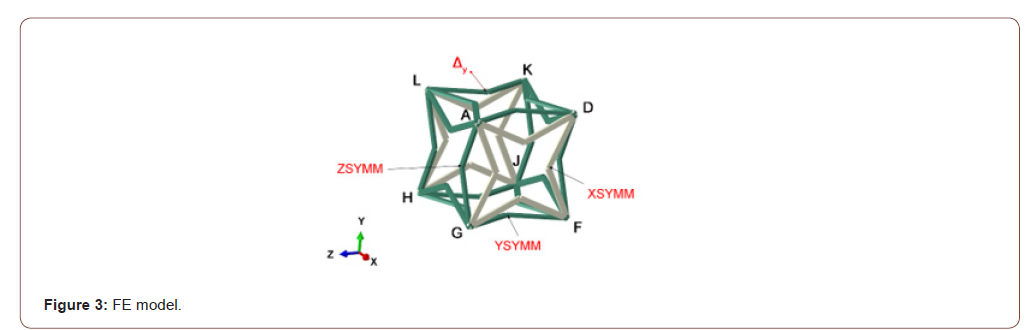
The unit cell of the proposed novel 3D star-shaped ZPR honeycomb is a regular hexahedron surrounded by six 2D star-shaped ZPR honeycombs of the same size. As shown in Figure 1, the length of the strut is defined as l , the section of the strut is t × t, the slant angle between the struts is 2θ, and the equivalent length of the unit cell is 2L = 2l sinθ This work is to study the star-shaped honeycomb of the concave octagon, so we define.45O< θ<90O.

Analysis of the Equivalent Elastic Properties
Because of the cubic symmetry of its cellular units, the novel honeycomb proposed in this study has the same equivalent elastic properties in three principal directions, which are not impacted when the scale of honeycombs is a × b × c,a ≠ b ≠ c. In this paper, 1/8 of the unit cell is selected as a simplified structure for analysis, and only the situation under uniaxial load in the Y direction is discussed (Figure 2 (a)). Assuming that the longitudinal displacement
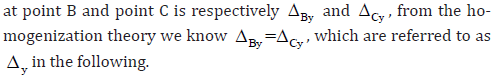
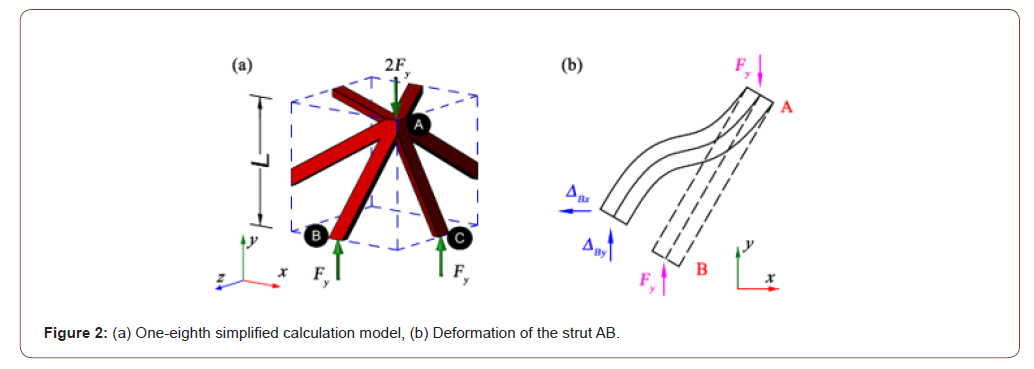
Equivalent Poisson’s ratio
When the simplified structure is subjected to the load in the Y direction, deformation only occur with strut AB and strut AC, and the vector of the lateral displacement at point B and that at point C both point to the interior of the unit cell, which has nothing to do with the equivalent transverse strain. Therefore, the equivalent transverse strain is
εx =εz = 0(1)
and the equivalent Poisson’s ratio is obtained to be
νyx =νyz = 0(2)
Namely, the proposed structure is zero Poisson’s ratio honeycomb.
Equivalent young’s modulus
In the next we derive the equivalent Young’s modulus based on Timoshenko beam theory. From the principle of virtual work
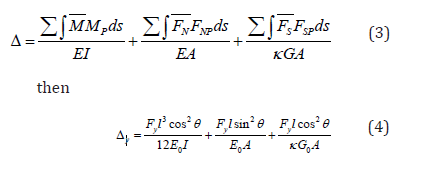

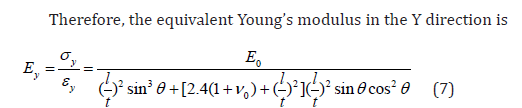
Numerical Analysis
In order to verify the analytical results above, the unit cell shown in Figure 1(c) is numerically analyzed using the Timoshenko beam unit B31, and the size is divided by 0.1. The finite element (FE) results are shown in Figure 6 with the boundary condition shown in Figure 3. In addition, the node displacements of planar HJKL and planar DFJK were coupled by constraint equations for uniform expansion of cell units.
Experiment
In order to verify the theoretical results and the finite element results, three sets of samples are prepared by the 3D printer of the SLA principle (Figure 4(a)). The geometrical parameters of the samples are listed in Table 1 and the scale of honeycombs in each set is 6× 6× 6 . The elastic modulus of the base material is 2286MPa and the Poisson’s ratio of the base material is 0.397 . A compression test is performed on the samples with quasi-static load with the speed of 0.2mm min by a universal material testing machine. Micrometers are set around the sample to obtain the deformation in another two principal directions, as shown in Figure 3(b).

Table 1:The geometrical parameters of the specimen.

Results and Discussion
Figure 5 shows that when the uniaxial compression is loaded in the Y direction, transverse displacements of the same value simultaneously occur with the central nodes in the X direction and the Z direction, while no transverse displacements occur with the corner nodes. The FE results are in consistency with our discussion in section 3.1. This result verifies that the structure designed in this paper is zero Poisson’s ratio honeycomb and reveals the formation mechanism of zero Poisson’s ratio effect.
It can be seen from Table 2 that the analytical results are in good agreement with the FE results, namely vyx=vyz=0, and that there is a slight deviation in the experimental results. The reason for this deviation may be i. There are manufacturing errors in the 3D printed test specimens; ii. There exist certain zones where thin struts overlap and interlace in the manufactured honeycomb; iii. The influence of boundary conditions exists when the number of unit cells is small.
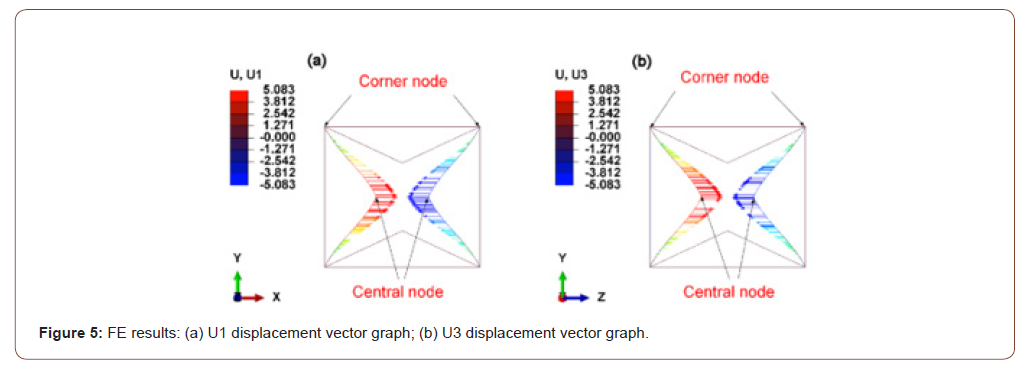
Table 2:Comparison of the analytical, numerical and experimental results.
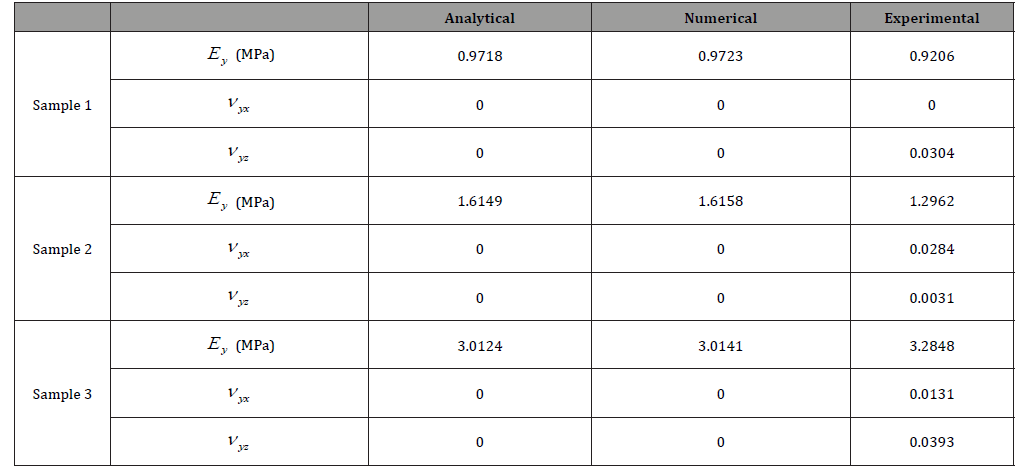
Figure 6 shows the influence of geometric parameters on normalized Young’s modulus EY/E0 and equivalent Poisson’s ratio vyxor(vyz). The results show that the FE results are in good agreement with the curves of the analytical formula, and the normalized Young’s modulus EY/E0increases with the increase of θ or t/l, and the growth rate first slows down and then increases rapidly. The results also show that the changes of θ and t / l have no effect on the performance of zero Poisson’s ratio.

In this paper, we only pay attention to the honeycomb with low relative density and do not consider the overlap area of thin struts. According to Figure 2, the relative density is
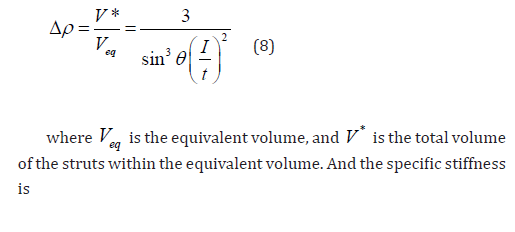

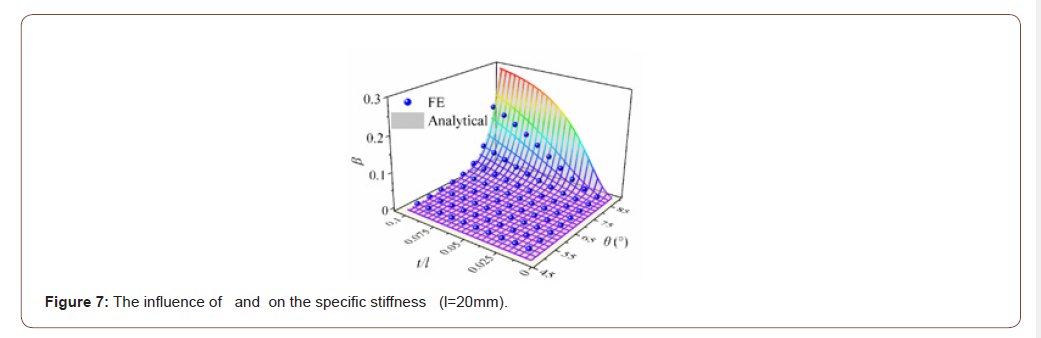
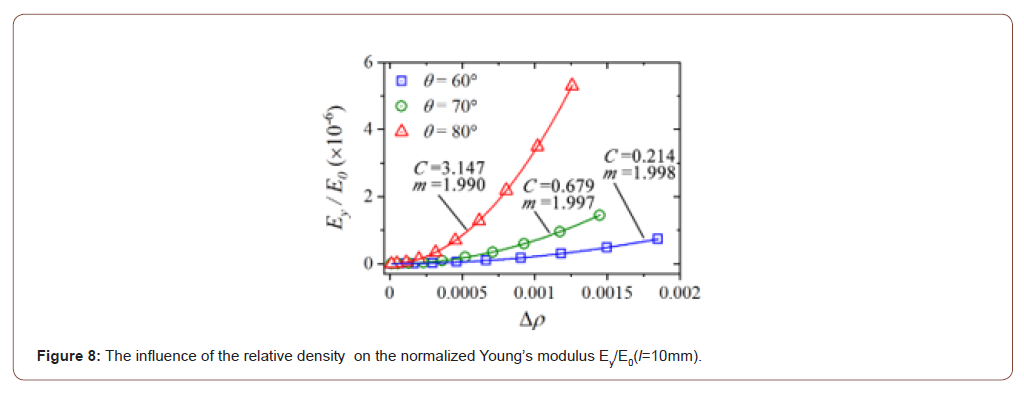
Figure 7 shows the influence of the novel honeycomb’s geometric parameters in comparison with the FE results and the analytical solutions. The results show that the specific stiffness β increases with the increase of the slant angle θ , and the growth rate first slows down and then increases rapidly, while β also increases with the increase of the width to height ratio t / l of the thin strut, and the growth rate first increases rapidly and then tends to slow down. Figure 8 shows the relationship between the normalized Young’s modulus and the relative density obtained from the analytical solution. It can be seen from Figure 8 that the normalized Young’s modulus is approximately equal to the square of the relative density. That is, bending deformation is the dominant deformation mechanism of the new three-dimensional zero Poisson’s ratio honeycomb.
Conclusion
In this paper, a novel three-dimensional (3D) star-shaped zero Poisson’s ratio (ZPR) honeycomb with cubic symmetry is developed based on a two-dimensional (2D) star-shaped ZPR honeycomb. An analytical model is developed to investigate the Young’s modulus of the proposed new honeycomb, which is verified by the finite element (FE) results and the experimental results. The influence of the geometric parameters (the inclination angle θ and the widthto- height ratio t / l of the thin struts) on the honeycomb’s elastic performance is studied in detail.
The results show that the proposed honeycomb has ZPR effect in three principal directions with the same equivalent Young’s modulus. Moreover, the increase of the width-to-height ratio t / l of this new honeycomb’s struts improves the stiffness of the material without having any impact on the ZPR effect. Therefore, the novel honeycomb is of good application prospect in various fields, such as anti-collision facilities and wing morphing.
Acknowledgement
This work was supported by the National Natural Science Foundation of China (11502172), the Featured Innovation Project from Education Department of Guangdong Province (2016KTSCX143) and the Scientific Research Funds of Wuyi University (31013009).
Conflict of Interest
No conflict of interest.
References
- Kshetrimayum RS (2005) A brief intro to metamaterials. IEEE Potentials 23(5): 44-46.
- Lakes R (1987) Foam Structures with a Negative Poisson’s Ratio. Science 235: 1038-1040.
- Evans KE, Nkansah MA, Hutchinson IJ, Rogers SC (1991) Molecular network design. Nature 353(6340): 124-125.
- Fu MH, Chen Y, Zhang WZ, Zheng BB (2016) Experimental and numerical analysis of a novel three-dimensional auxetic metamaterial. Physica Status Solidi B 253(8): 1565-1575.
- Fu MH, Liu FM, Hu LL (2018) A novel category of 3D chiral material with negative Poisson’s ratio. Composites Science and Technology 160: 111-118.
- Grima JN, Oliveri L, Attard D, Ellul B, Gatt R, et al. (2010) Hexagonal Honeycombs with Zero Poisson’s Ratios and Enhanced Stiffness. Advanced Engineering Materials 12(9): 855-862.
- Attard D, Grima JN (2011) Modelling of hexagonal honeycombs exhibiting zero Poisson’s ratio. physica status solidi (b) 248(1): 52-59.
- Grima JN, Attard D (2011) Molecular networks with a near zero Poisson’s ratio. physica status solidi (b) 248(1): 111-116.
- Chen JJ, Shen X, Li JF (2015) Zero Poisson’s ratio flexible skin for potential two-dimensional wing morphing. Aerospace Science and Technology 45: 228-241.
- Lu C, Li YX, Dong EB, Yang J (2013) Equivalent Elastic Modulus of Zero Poisson’s Ratio Honeycomb Core. Journal of Materials Engineering 3(12): 80-84.
- Liu WD, Li HL (2018) Equivalent Moduli of Accordion Honeycomb with Zero Poisson’s Ratio. Chinese Journal of Solid Mechanics 39(01): 100-112.
- Gong XB, Huang J, Scarpa F, Liu YJ, Leng JS (2015) Zero Poisson’s ratio cellular structure for two-dimensional morphing applications. Composite Structures 134: 384-392.
- Huang JL, Liu WY, Tang AM (2018) Effects of fine-scale features on the elastic properties of zero Poisson’s ratio honeycombs. Materials Science and Engineering: B 236-237: 95-103.
- Zou TT, Zhou L (2017) Mechanical property analysis and experimental demonstration of zero Poisson’s ratio mixed cruciform honeycomb. Materials Research Express 4(4): 045702.
- Rong JX, Zhou L (2017) Study of a zero Poisson’s ratio honeycomb used for flexible skin. Materials Research Express 4: 045701.
- Cheng WJ, Zhou L, Zhang P, Qiu T (2015) Design and analysis of a zero Poission’s ratio mixed cruciform honeycomb and its application in flexible skin [J]. Acta Aeronautica Et Astronautica Sinica 36(2): 680-690.
- Olympio KR, Gandhi F (2010) Zero Poisson’s Ratio Cellular Honeycombs for Flex Skins Undergoing One-Dimensional Morphing. Journal of Intelligent Material Systems and Structures 21(21): 1737-1753.
- Chen Y, Fu MH (2018) Mechanical Properties of a Novel Zero Poisson’s Ratio Honeycomb. Advanced Engineering Materials 20(2): 1700452.
- Liu WD, Li HL, Zhang J, Li HD (2018) Elastic properties of a novel cellular structure with trapezoidal beams. Aerospace Science and Technology 75: 315-328.
- Liu WD, Li HL, Zhang J, Bai YL (2019) In-plane mechanics of a novel cellular structure for multiple morphing applications. Composite Structures 207: 598-611.
- Huang J, Gong XB, Zhang QH, Scarpa F, Liu YJ (2016) In-plane mechanics of a novel zero Poisson’s ratio honeycomb core. Composites Part B: Engineering 89: 67-76.
- Huang J, Zhang QH, Scarpa F, Liu YJ, Leng JS (2016) Bending and benchmark of zero Poisson’s ratio cellular structures. Composite Structures 152: 729-736.
- Huang J, Zhang QH, Scarpa F, Liu YJ, Leng JS (2017) Shape memory polymer-based hybrid honeycomb structures with zero Poisson’s ratio and variable stiffness. Composite Structures 179: 437-443.
- Fu MH, Zheng BB, Li WH (2017) A novel chiral three-dimensional material with negative Poisson’s ratio and the equivalent elastic parameters. Composite Structures 176: 442-448.
- Ha CS, Plesha ME, Lakes RS (2016) Chiral three-dimensional isotropic lattices with negative Poisson’s ratio. Physica Status Solidi B 253(7): 1243-1251.
- Xia R, Song XK, Sun LJ, Wu WW, Li CL, et al. (2017) Mechanical properties of 3D isotropic anti-tetrachiral metastructure. Physica Status Solidi B 255(4): 1700343.
- Ren X, Shen J, Ghaedizadeh A, Tian HQ, Xie YM (2015) Experiments and parametric studies on 3D metallic auxetic metamaterials with tuneable mechanical properties. Smart Materials and Structures 24(95016).
- Ai L, Gao XL (2018) Three-dimensional metamaterials with a negative Poisson’s ratio and a non-positive coefficient of thermal expansion. International Journal of Mechanical Sciences 135: 101-113.
- Lu ZX, Wang QS, Li X, Yang ZY (2017) Elastic properties of two novel auxetic 3D cellular structures. International Journal of Solids and Structures 124: 46–56.
- Wang NL, Liu WY, Tang AM, Huang JL, Lin ZQ, et al. (2014) Strain isolation: A simple mechanism for understanding and detecting structures of zero Poisson’s ratio. physica status solidi (b) 251(11): 2239-2246.
- Chen Y, Zheng BB, Fu MH, Lan LH, Zhang WZ (2018) Double-unusual 3D lattice honeycomb displaying simultaneous negative and zero Poisson’s ratio properties. Smart Materials and Structures 27: 045003.
- Yang H, Ma L (2018) Multi-stable mechanical metamaterials with shape-reconfiguration and zero Poisson’s ratio. Materials and Design 152: 181-190.
- Yang H, Ma L (2019) Multi-stable mechanical metamaterials by elastic buckling instability. J Mater Sci 54: 3509–3526.
- Grenestedt JL (1999) Effective elastic behavior of some models for perfect cellular solids. International Journal of Solids and Structures 36(10): 1471-1501.
-
Zhang Wenzhi, Jie Dianmin, Li Zhiwei, Song Nanxin. A 3D Star-Shaped zero Poisson’s Ratio Honeycomb with Cubic Symmetry. Glob J Eng Sci. 7(2): 2021. GJES.MS.ID.000660.
-
Environment, Heterogeneous, Computing, Akka library
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






