On the Same Origin of Quantum Physics and General Relativity from Riemannian Geometry and Planck Scale Formalism

Introduction

The unification of the Einstein field equation and quantum theory still lacks a clear and consistent bridge between the two. All theories in the literature require unproven assumptions or inconsistencies. This work bridges the gap between the two theories. We propose that universe could be considered as composing of pixels of space and time entangled together in Planck scale. In recent years, the James Webb Space Telescope (JWST) has observed several phenomena, including galaxies that had already existed 300 Myr after the big bang, which have never been thought to exist (Boyett et al, 2024; Mann, 2023) [2, 3]. However, our proposed theory suitably explains this phenomenon.

In addition, the discovery of the Big Ring structure challenges the cosmological principle, which posits that the universe should look roughly the same everywhere, on a large scale. The existence of such ultra large structures like the Big Ring and the Giant Arc questions this fundamental assumption in cosmology.

The equation proposed in this study can be used to explain this phenomenon: Our work also explains this finding.

Another conjecture in physics is whether the Einstein-Rosen bridge (ER) and Einstein-Podolsky-Rosen (EPR or entanglement) are physically equivalent. The ER=EPR conjecture awaits rigorous proof (Susskind, 2016) [4]. This work also provides further proof of this claim. This work is different from other attempts at unification: (i) string theory, which still lacks experimental observation of extra dimensions (Green & Schwarz, 1984; Dienes, 1997; Krasnov & Percacci, 2018) [5-7], (ii) loop quantum gravity, which still faces challenges in its compatibility with the Standard Model (Rovelli, 2008) [8]. In our study, we assume that the new equation should be written in a unitless manner on the Planck scale. Current physical models require at least ten physical constants. Meanwhile, there remain only two constants used in this framework: Planck length and Planck time. In addition, the proposed equation can explain the Gravitational Wave Background (GWB) observed over 15 years by NANOGrav (Agazie, et al. 2023) [9].

Applying the Onsager principle on reciprocal relation to the Einstein field equation (EFE), we infer that if a mass can create a curvature (EFE), the curvature can also create a mass. We recap the Ricci tensor before proving each claim in this work. An important concept inferred from the proposed equation is that relaxation of the curvature can create a mass. Because this is a theoretical work, it is organized by topic rather than by an ordinary experimental article structure.

The Ricci tensor R_ij, stands as a fundamental mathematical form of the curvature inherent to a Riemannian manifold (Einstein & Kaufman, 1955; Schouten, 2013) [10, 11]. It is derived from the Riemann curvature tensor R_ijk^l by contraction. This can be expressed as R_ij = R_ikj^k where we take the summation convention over repeated index K . The Ricci tensor is symmetric, that is, R_ij= R_ji , and in a local coordinate system, it can be expressed in terms of the metric tensor g_ij and its derivatives. The Ricci tensor is used to describe the curvature of space-time in Einstein’s field equations and is integral to the study of Einstein manifolds, Ricci flow, and scalar curvature. Although it encapsulates important geometric information, the Ricci tensor does not fully characterize the manifold curvature, a task reserved for the full Riemann curvature tensor. Its utility lies in its simpler structure compared with the Riemann tensor, which facilitates analyses in various geometrical and physical contexts.

A. Planck Units

In this work, we applied Planck length and Planck time to form a Plack-scale invariant equation in addition to the form of a covariant field equation. The Planck length, denoted by p l , is the smallest measurable unit length. The Planck length embodies this inherent limitation, signifying the smallest possible region in which a particle can be localized, owing to its associated momentum uncertainty. Mathematically, the Planck length is expressed as (Amelino-Camelia, 1996; Vasileiou, et al 2015) [12, 13].

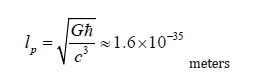
where G is the gravitational constant,  is the reduced Planck’s constant, and c is the speed of light. Planck time is intimately linked to Planck length is the Planck time, which is denoted by t_p . It represents the smallest measurable unit of time and is derived from the Planck length and the speed of light. Planck time signifies the minimum duration over which any meaningful physical process can occur [1]. Mathematically, the Planck time is expressed as

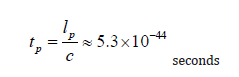
These minuscule quantities are far beyond the reach of our current technology and likely represent the fundamental granular nature of space-time at the quantum level. Understanding these concepts is crucial for effectively applying the unification of gravity and quantum theories, as they represent the scales at which both theories are expected to converge (Callender & Huggett, 2001) [14]. We propose an equation that is unitless on a Planck scale. The equation can be derived into the Dirac equation, Maxwell’s equations, quantum electrodynamics, the Klein-Gordon equation, Einstein Field Equation, and calculation of quark masses as well as neutrino masses (electron, tau, and muon), which are valid compared to the Standard Model (De Gouvêa, 2016; Bilenky, et al. 2003) [15, 16]. The proposed equation could potentially explain the existence of the galaxies observed by the JWST in the early universe (which was not supposed to exist) and the theory’s implications on the evolution of the universe.

B. Ricci tensor formulation in terms of covariant derivative

One could see that the Ricci tensor

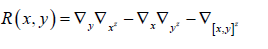
Assume ∇_{[x, y]}Z is negligible and extremely nonlinear, we get

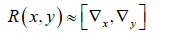
Then to make it symmetric, we can add permutation symbol σ (x, y) :

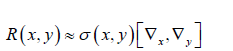
Since we included +/− signs in the later equations in the article, adding a permutation symbol will not propagate errors through the rest of the paper. For simplicity, we will use Dinstead of Δ .

From Riemannian Geometry (Petersen, 2006) [17], Ricci curvature is defined as the commutator covariant derivative of a vector in a manifold in different directions. We can write the Ricci tensor as:

where Rμν is the Ricci curvature tensor, ψ^A is a vector in the manifold or spacetime, D_μ is the covariant derivative in the coordinate x^μ in spacetime, and σ (μ,ν )is permutation symbol to make the Ricci tensor symmetric. We will omit the terms σ (μ,ν ) and ψ^A for the rest of the derivations where these terms can be resolved after derivations on operators has been rearranged.

THE UNIFIED EQUATION

According to Einstein Field Equation in General Relativity (Einstein & Kaufman 1955; Einstein, 1916) [10, 18].

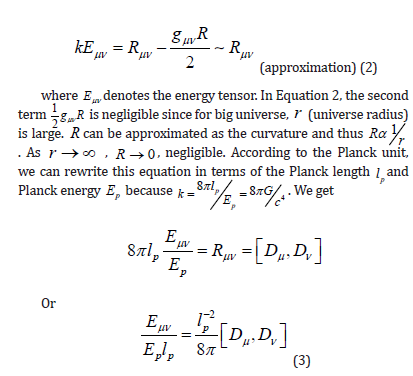
DIRAC EQUATIONS FROM EINSTEIN FIELD EQUATIONS

This section provides mathematical proof that a unified equation implies a Dirac equation with an electromagnetic (EM) gauge with curvature relaxation or inflation. From equation (3), since

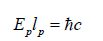
and assume Lie group of D_μ over spacetime manifold, we obtain

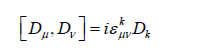
where ε^k_μν is the coefficient tensor from symmetry group of D_μ operating on the wavefunction of the manifold. Upon normalizing

to a unitless covariant derivative, we arrive at

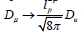
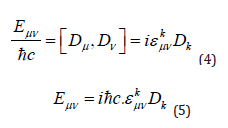
Upon contraction, the approximated coefficient tensor become Dirac matrices (γ^k=g^μν ε^k_μν)

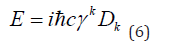
where γ^k are Dirac matrices. Finally, we derived the Dirac equation (DE) for a zero-mass object (Dirac, 1933; Thaller, 2013) [19, 20]. The wave function can be written as ψ=e^ikμxμ, where k andx are four-component vectors,

and x = [x, y, z,ct] . Dk (Eq.6) is also a four-component vector.

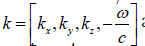
Therefore,

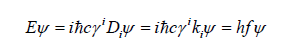
which is the quantum energy of photon with no mass. We can omit the wave function and manipulate the operator and solve it later. Regarding to the Christoffel symbols, the contraction could be made to 1-rank vector like this

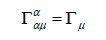
It is normal to make it to the same rank of covariant derivative D_μ .

Consider equation (4) using the definition of D_μ=D_μ'±Γ'_μ, where Γ'_μare the Christoffel symbols from the curvature of the new spacetime coordinate:

Because R'_μν in unit of E/c equal to the LHS, we have

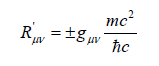
From equation 4, we deduce that

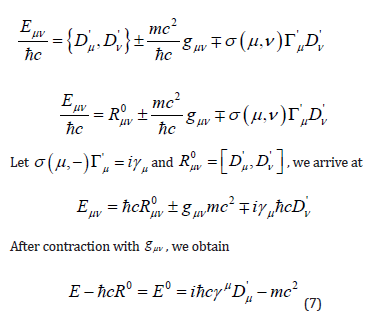
where E⁰ is the effect of energy after resetting the new curvature of spacetime in a new reference frame. Thus, Equation 7 is the Dirac equation, which is a relativistic quantum theory.

THE EINSTEIN’S SPECIAL RELATIVITY IN CURVED SPACETIME FORMALISM

From the Einstein Field Equation (EFE) in Riemannian geometry (Stephani et al, 2009) [22] and the Planck formalism, we can derive relativistic quantum mechanics equations for fermions. Therefore, there is a corresponding one-to-one mapping from EFE to DE for both zero mass and mass.

We can say that they are the same equations that we will elaborate further on in the next section.

In conclusion, equation 7 could be rewritten as

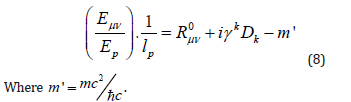
The Klein-Gordon equation (Bruce & Minning, 1993) [23] can be derived from our proposed equation, as follows: Taking the square of equation 8, we deduce:

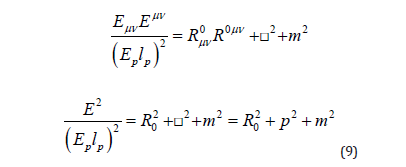
Equation 9 is the Klein-Gordon equation, which describes bosonic particles with curvature tensors as additional terms:

ELECTROMAGNETIC FIELD AND THE MAXWELL’s EQUATIONS

Upon promoting operator D_μ to add A_μ vector potential with coupling e to the gauge, c is the velocity of light:

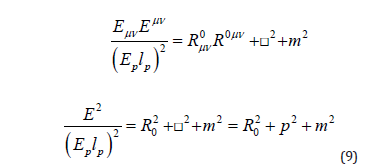
Introducing the gauge into equation (7), we have

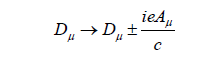
A. Derivation of Maxwell’s equations

Suppose the term in imaginary part cancel each other out and equal to zero.

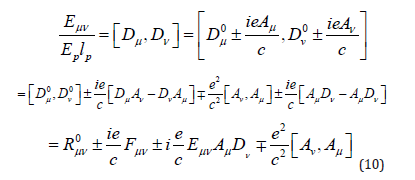
Consider its partial derivative,

Suppose e = 1/L , and we proved Maxwell’s equations in (11). From (10), with the imaginary term cancelled out as Maxwell’s equation and the relation between the electron mass and charge in terms of curvature, we again obtain the Dirac equation.

B. Field theory of Electromagnetics

Next, we obtained the gauge term in EM theory. Taking the square root of equation (12), we obtain

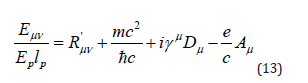
By offsetting the Ricci and energy terms, we obtain the Field Theory of Electromagnetics, which is a differential equation with an additional gauge vector field A_μ for electron-photon interactions. The gauge vector was introduced into the following equation:

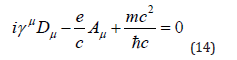
CHROMODYNAMICS: QUARK AND GLUON FIELD THEORY

From the unified equation, we promote a

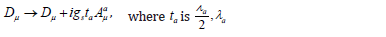
is the Gellman matrix, a is the gluon field, and g_s is the coupling constant.

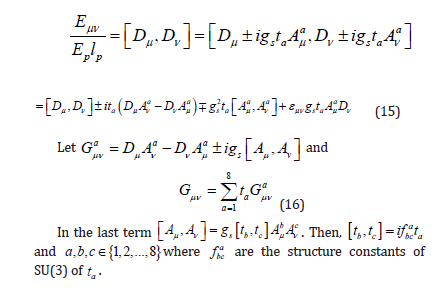
From equation (1),

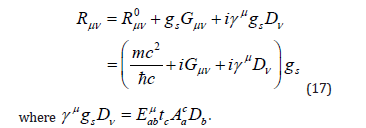
Taking square of (17) and square root back gives

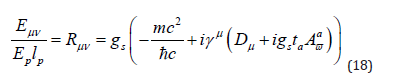
Equation 18 is Dirac equation of motion for gluons and quarks.

CURVATURE RELAXATION AND MASS GENERATION

The relaxation of R which describes a curvature larger than R0 results in R⁰ with the momentum and mass. Therefore, as the universe expands, it produces both mass and kinetic energies. In other words, the curvature is converted into mass and kinetic energy, known as momentum, electrons, or photons (or quarks and gluons), as discussed in the previous section. Figure 1 depicts the reciprocal relation (Onsager principle) that mass creates curvature (Einstein’s field equation), and that relaxation of curvature to flat space, for example, Hawking radiation process, can create mass.

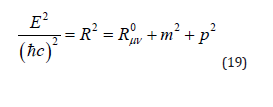
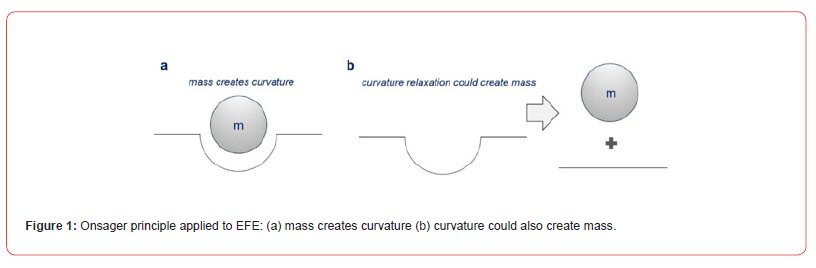
The proposed equation can compute the masses of up and down quarks and neutrinos (electron, muon, and tau), which is consistent with the Standard Model (SM).

A. Electron mass and quark masses

We begin with electron and quark mass calculations using the proposed equations, which conform to the values from the Standard Model. Subsequently, we derived the masses of the neutrinos (electrons, muons, and tau). According to equation (10), where the last term is the interaction term, we arrive at

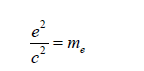
The charge must be converted into a unit of Coulomb interactions. Thus, we added the terms electric and magnetic field interactions and obtained the correct unit of electron charge.

Charge of electron can be calculated by

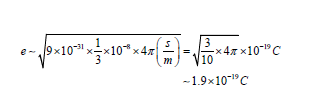
which is close to actual value of 1.6×10⁻¹⁹C. In conclusion

According to Feynman’s Lecture, rest mass should be resulted from self energy interaction of electron hence the term mα e² . However, dimension was not correct, since we need to convert to coulomb unit for e (charge of electron). The reason it is 1.9×10⁻¹⁹C and not 1.6×10⁻¹⁹C is because we need Feynman in higher order terms.

E=mc²=hc/λ.In normal standard practice we can set c =1, h =1. Therefore, using dimensional analysis

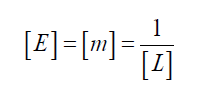
Is that make sense to you as physicists. Since as you read through the paper, the size of the maximum universe should be 1/l_p=R_maxand the m_e should be proportional to 1/R_max which is l_p .

According to Feynman’s lecture, m is proportional to e² which is self-interaction. Of course, we need to convert the unit of charge e to coulomb. Therefore, the term of constants in electrostatics

and which is used to calculate forces between electric and magnetic field.

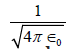
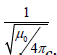
As the universe expands, the charge and mass of electrons decreases, resulting in less interaction in the aging universe. The electron charge and mass are no longer constant. They depended on the radius of the universe at the time. There are several papers reported about variable fine-structure constant at various parts of the universe (Webb et al., 2011) [24]. Hence so do the electron mass.

We can consider the mass of the quark in terms of the mass of the electron in the same way, considering the charge. For the up and down quarks, the charges were 2/3e and −1/3e e respectively. Because a quark is equivalent to a confined electron in the fractal dimension of space-time, it results in a larger interaction energy.

The mass of the down quark, md should be proportional to (3e)² because we divide the electron into 1/3 fractal dimensions. Hence,

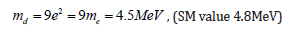
the same reason for up quark is for fractal dimension 1/2. Therefore, its mass

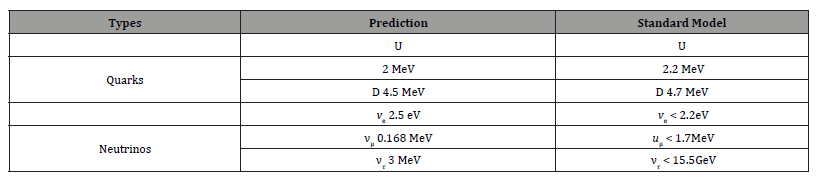
We wrap up the masses calculated from our theory and compare them with the Standard model as follows (Table I).

Table 1:Summarized table of masses computed from the proposed equation (Green) and the Standard Model (Blue) [25-28].

The occurrence of neutrino oscillations could possibly be caused by uncertainty in the hierarchies of the curvature. The charges of the neutrinos disappear because they are fermion particles in the universe with zero curvature (radius is infinity; E² = mc = c/L , L approaches infinity as E approaches zero).

At Planck scale l_p , the eigen solution to the unified equation is

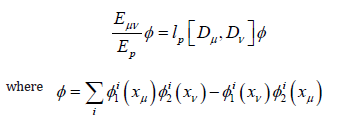
which are entangled wavefunctions.

MASS OF LEPTONS (ELECTRON, MUON, TAU, WITH THEIR NEUTRINOS)

The Christoffel symbol μ Γ is a key component of the local curvature resulting from self-interaction and interaction with the Ricci Tensor (curvature tensor).
• This local curvature results in a mass of particles owing to its local curvature and the surrounding environment.
• If we have two curvature overlaps, according to Gauss’s curvature, the new curvature would be the geometric mean of the curvature; for example, curvature K₁ has radius R₁ and curvature K₂ has radius R₂ . Combining these yields the curvature

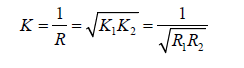
For this reason, we assume the hierarchy of curvature as in Figure 2, which illustrates the hierarchical curvature of universe, galaxy, and solar system, respectively.

The masses of electrons, muons, and tau can be explained by the different curvatures of universe, galaxy, and solar system, respectively.

We assume R_U , R_g and R_s stand the radii of universe, galaxy, and solar systems, respectively.

Therefore,

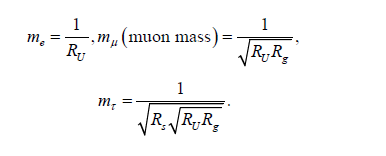
Rearrange the terms for m_μ and m_τ ,

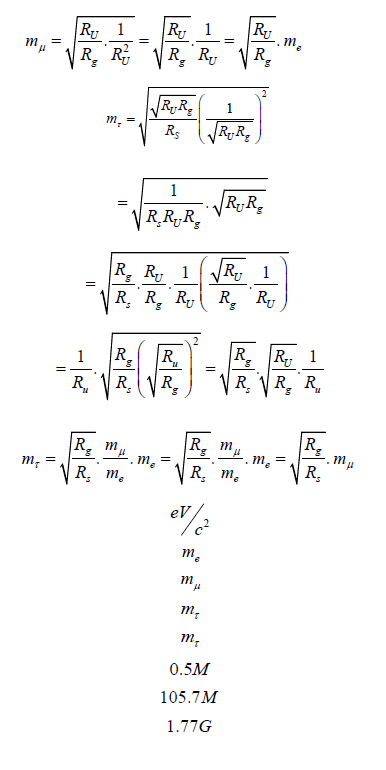
Table II. Masses of electron, muon and tau from the Standard Model. This will be used to compute the ratio in relation to the solar system/galaxy/universe radii.

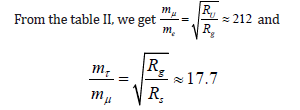
These parameters were used to calculate the mass of their neutrino counterparts, m_νe, m_νμ, and m_ντ or the mass of (electron, muon, and tau) neutrinos, respectively. Assume m_νe is the mass where the maximum radius of the universe takes place.

We wrap up the masses calculated from our theory and compare them with the Standard model as in table I.

PLANCK SCALE AND THE SPACE-TIME ENTANGLEMENT

In Planck scale, it is entangled wavefunction between space and time, which is

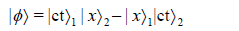
Therefore, singularity at the Planck scale should not occur from the collapsing black hole (BH) because the operation on ϕ for collapsing spacetime is a permutation of space and time. Hence,

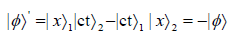
resulting in the reversal of the sign of the wavefunction, and thus the expansion of the newborn universe or the so-called white hole (WH).

The entangled |φ 〉 for the BH state implies that as t increases, x decreases at the Planck scale with a toggle between x and ct . Therefore, as t increases, x increases in the WH state φ 〉' .
XI. ER = EPR

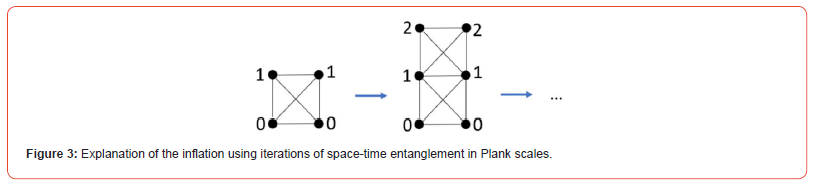
The conjecture that ER = EPR can be proved in our formulation (Figure 3). Before we discuss whether ER = EPR, we consider the space-time entanglement between a universe and its conjugate.

A. Space-time entanglement between universe and conjugated universe Λ'_μν

can absorb the momentum and mass terms, increase its curvature, and turn into Λ'_μν

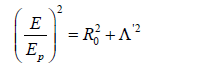
Λ'_μν could then be relaxed and release mass in its universe, then

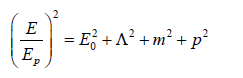
Therefore, if two universes are entangled, we can send an energy of E₀²= m² + p² to another universe via curvature encoding or holographic coding. Next, we consider the cases of black hole and white hole. For conventional approach to ER = EPR proof using feynman path integral, please see (Srichan, 2024) [29].

B. BH & WH entangled with no singularity

As discussed earlier, singularity from collapsing the BH can be avoided at the Planck scale by space-time inversion. Suppose that the wave function of the BH can be described by

where α (t) is the scaling factor for φ₀ and increase with time. Consider

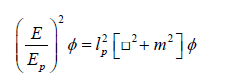
where φ is eigen wave function for space & time.

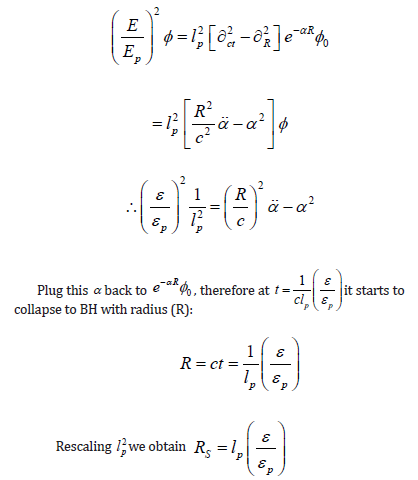
However, one qubit is equivalent to two classical bits, therefore Schwarzschild radius should be multiplied by 2. Therefore,

Now we derived R_S as the Schwarzschild radius.

As the BH collapses and reach l_p , Planck-scale eigenfunction change its sign.

Therefore, it stops collapse and start to expand instead due to | x〉 and | ct〉 interchange. This results in a newborn WH or universe.

Because BH and WH are entangled and conjugated, we can write the unified equation as

Hence, energy transfer from particles falling into the BH can be transferred to the WH or conjugated universe via the same scenario, similar to the case of lambda. Experimental energy transfer via entanglement was reported by Gómez-Ruiz (2023) [30].

This could solve the information loss paradox in BH, as JWST can see light and galaxies before a big bang from the conjugated universe.

3) EPR = ER in the same universe In this case, we have to rewrite the unified equations to

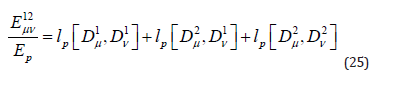
EIGENSOLUTION

The eigensolution is therefore

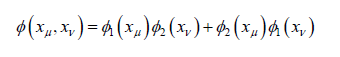
which is an entangled state. Upon squaring (25),

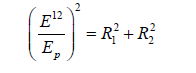
We used the same method to transport energy between entangled spaces R₁ and R₂ in the same universe (Gómez-Ruiz, et al. 2023) [30].

GRAVITY IN EM FIELD THEORY

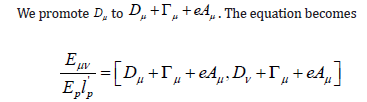
where Γ_μ denotes the Christoffel symbol. From the above equation, we use the same method as Γμ promotes to Γ_μ + eA_μ. Therefore

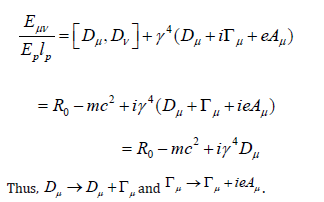
Finally, we obtain the Dirac Equation with gravitational term Γ_μ included. The term Γ_μ absorbs EM and quark-gluon interactions and creates a local curvature and hence the mass of the particles.

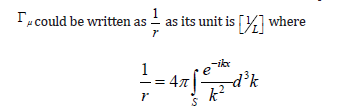
This is similar to a gauge with no charge, in which the mass cancels out the term eA_μ to be absorbed into the local curvature for EM interaction. Therefore, we can calculate the mass directly from the interaction term. Hence, graviton could be quantized according to EM vector A_μ which is actually similar to photon with no mass using above expression.

Discussion

A. Entangled space-time

According to the unified equation, we consider space and time component:

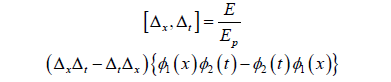
Let the minimal physical meaning length and time be l_p and t_p , then

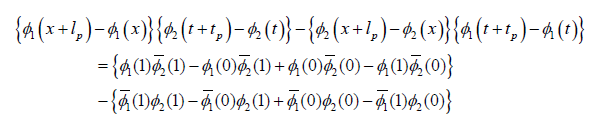
where, for simplicity, (1) either represents x + x_p or t + t_p and (0) represents either x or t respectively, depending on whether the term is for time or space. The bar (φ ) denotes time and φ denotes the space states. The state can then be written as

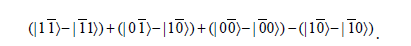
The step-by-step creation of particles using space and time entanglement is illustrated in Figure 3. This process occurs iteratively as the plank time and length increase during inflation.

B. Why universes cannot collide?

According to bosonic unified equation,

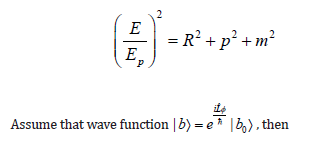
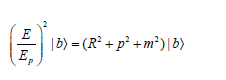
Square root of the equation above yields

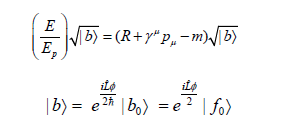
where | f₀ 〉 is fermion wave function. Therefore, the universe should carry half-integer spin and are all fermionic. Hence, the Pauli exclusion principle rules out the possibility of collision between universes.

C. Increasing velocity of objects far away from a galaxy

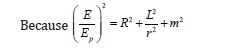
is constant, L is constant if r is the radius of the galaxy.

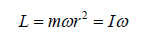
and ω must be constant. Therefore, v_x =ωr_x

The velocity of the objects increases as their distance from the center of the galaxy increases because ω is constant. However, it should saturate when r_x approaches r because the curvature of the galaxy vanishes, including the screening effect.

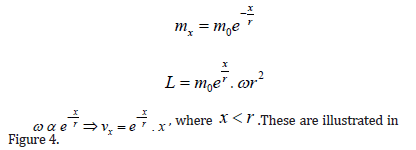
It is important to note that our proposed theory matches the galaxy rotation curves (Honma & Sofue 1997).

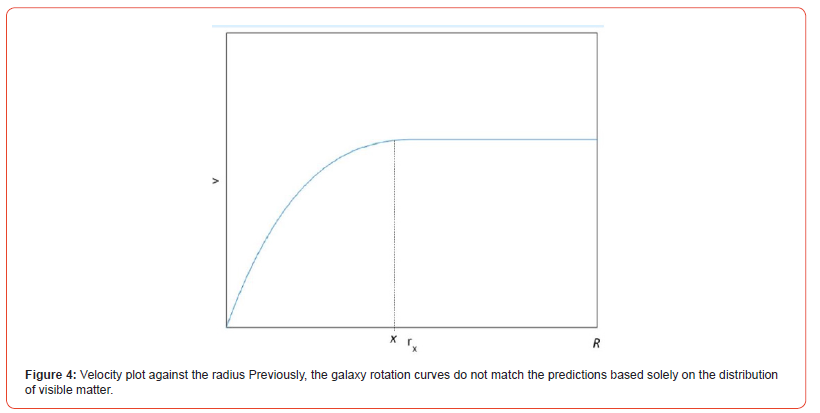
• Galaxies rotate faster than expected, especially for distant stars, and usually assume the existence of dark matter, a hypothetical matter.
• Our derivation complies with the experimental observation that as the distance (from the galaxy center) increases, the velocity of the stars increases without any additional assumptions. This is an obvious implication from equation (26):

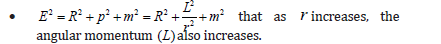
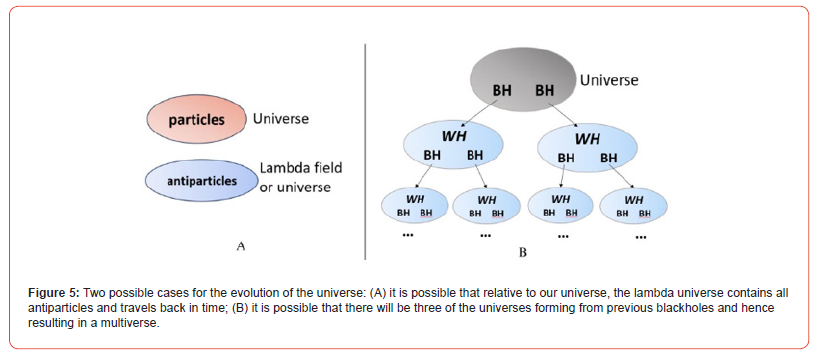
D. Two possibilities

As predicted by the proposed equation, the evolution of universes over time can be divided into two distinct schemes, as shown in Figure 5.

Conclusion

From Riemannian geometry, we can prove that the Einstein Field Equation (EFE) is equal to the quantum equation by formulating in the Planck-scale unit. In addition to Einstein’s principle of covariance that any equation should be independent of a frame of reference, we add an additional requirement that the equation should also be unitless on the Planck scale. The equation shows that relaxation of the curvature induces the creation of mass and (angular) momentum. As the universe expands, the mass increases and finally reaches the point at which it stops expanding. We calculated the masses of the three flavor neutrinos as well as some quarks, owing to the hierarchical curvature and fractal dimension of the quarks. The masses of up/down quarks and masses of (electron, tau, and muon) neutrinos calculated using the proposed equation are consistent with the values from the Standard Model (Table I). At the smallest Planck scale, space and time are entangled and will toggle via a black hole collapsing and avoiding singularity, but instead become expanding space-time. There are two mechanisms by which the universe can form: (i) directly from the lambda field, (ii) from the previous black hole (Figure 5), and (iii) small bangs from the big bang, which resulted in the old galaxies and old black holes observed at the early universe by JWST.

We would like to add more that the big bang is like the fireworks which is so beautiful and elegant. It explodes or expands, big one bang with the small bangs adds up of all small explosion implying inhomogeneity of universe. This small explosion or curvature relaxation gives rise to the mass. Hence, the old galaxies and black holes at the early universe that we have seen in JWST.

Last but not least, we would like to conclude new equation for special relativity should be
E2 = R2

and new equation for general relativity should be

These equations explain ER = EPR, old galaxies and black holes existence at the early universe, include dark energy contribution in the curvature energy when black hole collapse to the smallest Planck scale and therefore universe inflates. This new theory is compatible with quantum theory by considering Planck scale (Planck length and Planck time) as pixels or quantum bits of the universes.

MISCELLANEOUS: Fine structure might not be constant

Variations in fine structure constant have been observed and reported (Webb, et al. 2011) [24]. We propose a possible explanation on this. Since

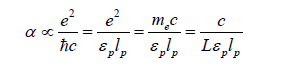
Where L is the universe radius. Therefore,

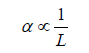
As the universe expands, the fine structure constant (α ) decreases. In addition, there is less interaction at a larger expansion of the universe. However, strong interaction occurs in the early universe, and it is possible that this accelerates the interaction of the early universe. We also found some structural objects in the early universe compared with the previous standard model.

Acknowledgement

None.

Conflicts of Interest

The author declares no conflict of interest.