On High-Order Compact Differencing Technique for Numerical Solutions of PDEs

High-order compact (HOC) differencing technique is an efficient numerical computational method for solving partial differential equations (PDEs) occurring in fields such as science, engineering, and finance. In early studies of the numerical methods, a standard three-point finite difference scheme for approximating the second order derivative usually results in a second order accuracy. To have a higher order of accuracy more points in the finite difference scheme would have to be used. In 1974, an idea of achieving a higher order accuracy, but still using three points, was suggested by Kreiss in a report [1], but no details of the method were provided, and it had not been tested. Ciment & Leventhal [2] used this proposed compact differencing method of fourth order accuracy in hyperbolic problems. Hirsh [3] presented the work investigating the feasibility and accuracy of this method by applying it to fluid mechanic problems. Ciment at el. [4] used the operator compact implicit method for solving parabolic PDEs associated with viscous fluid flow problems.

The HOC scheme was also applied to diffusion-convection problems [5-7] and to the Black-Scholes equations in finance [8-12]. Rigal [5] analyzed two-level three-point finite difference schemes of order 2 in time and 4 in space for studying the unsteady 1D diffusionconvection problems. The main focus is on finding an efficient finite difference scheme suitable for strongly convective problems. In [6] Steady-state HOC methods were applied to time-dependent problems for transient convection-diffusion in 1D and transient diffusion in 2D. Karaa & Zhang [7] studied the convergence analysis on some classical stationary iterative methods for solving twodimensional variable coefficient convection-diffusion equation discretized by a fourth-order compact difference scheme. Tangman, et al. [8] considered HOC schemes for quasilinear parabolic PDEs to discretize the Black–Scholes PDE for the numerical pricing of European and American options. In [9-11] HOC methods were used to discretize a nonlinear Black-Scholes equation that accounts for effects including transaction costs in portfolio hedging. During & Heuer [12] introduced a HOC scheme for parabolic PDEs with time- and space-dependent coefficients and mixed derivative terms in multiple dimensions. The method is shown to be fourth order accurate in space and second-order accurate in time, and its stability is analyzed for certain cases. The method is applied to the pricing of European power put basket options in a multidimensional Black- Scholes model.

A three-point non-uniform HOC scheme was derived using polynomial interpolation in [13,14]. Application of the method to numerical solutions of PDEs was also studied. In [15], a set of fourth order compact finite difference schemes was developed to solve a heat conduction problem with Neumann boundary conditions. The method was derived through the compact difference schemes at all interior points, and the combined compact difference schemes at the boundary points.

Here, we first present the derivation of the HOC scheme as described in 1975 by Hirsh [3]. As mentioned earlier, the usual objection to fourth order schemes comes from the additional nodes (besides the standard three) necessary to achieve the higher order accuracy. The additional nodes almost preclude the use of fourth order implicit methods since the matrix which arises is not the simple tridiagonal form produced by second order schemes. The disadvantage can be avoided by a finite differencing technique which is fourth order, and compact, that is, it retains tridiagonal form; hence, matrix inversion can be accomplished by the Thomas algorithm. The key step of the method is the introduction of the first and the second derivative functions of 𝑦_n, denoted as 𝐹_n and 𝑆_n, respectively. The standard second-order center difference schemes for 𝐹_n and 𝑆_n would be

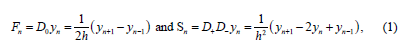
where the three difference operators: 𝐷₀, 𝐷₊, and 𝐷_-, are the center, forward, and backward differences, respectively. In order to achieve a higher order accuracy, we replace the 𝐹_n and 𝑆_n on the left-hand sides of (1) by an interpolation of 𝐹_n and 𝑆_n using the neighboring points. For a fourth order scheme as given in [3], we have

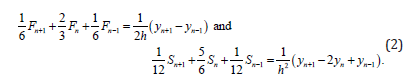
Notice that the tridiagonal form is retained in both equations in (2) for solving 𝐹_n and 𝑆_n, respectively. The fourth-order accuracy of both equations in (2) can be verified by a Taylor expansion and this gives the truncation errors as:

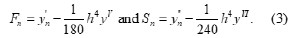
As mentioned in the Introduction, there are many applications of the HOC numerical schemes on solving modeling problems with PDEs. Here, we describe the application procedure as given in [3] and [6]. First, a simple Burgers’ equation which exhibits the interplay of convection and diffusion present in viscous flow problems is a good example (see [3]). After discretization, the system of the finite difference equations consists of three equations: the two equations in (2) and the finite difference form of the Burgers’ equation with the first and the second derivative functions of 𝑦_n denoted as 𝐹_n and 𝑆_n. At each time step, one can take advantage of the tridiagonal form of the two equations in (2) to solve the system of difference equations efficiently. In this system of difference equations, the time level on the first and second derivatives have not been specified in order to include both explicit and implicit options. For an explicit method, one can use the tridiagonal form of the two equations in (2) to solve for 𝐹_n and 𝑆_n first at each step and then substitute the values of 𝐹_n and 𝑆_n into the difference form of the Burger’s equation to perform time marching. For an implicit method, a block tridiagonal matrix (each block is 3 x 3) for the whole system of the difference equations needs to be used.

As a second example, the approaches for steady-state HOC difference methods can be extended to time-dependent problems as given in [6]. For transient convection diffusion equation, the extension can simply be done by treating the time derivative term as part of the source term. This generates a semi-discrete formulation for the transient problem and a class of time differencing methods, including the forward Euler, Crank-Nicolson, and backward Euler schemes can then be used. Other issues such as the stability and compact treatment of boundary conditions can also be studied.

HOC differencing technique provides efficient numerical methods for solving practical application problems. Derivation of the method as well as the procedure incorporating time derivative and the initial and boundary conditions are described. Further studies of HOC schemes regarding the numerical analysis topics including accuracy, convergence and stability are needed. Also, applications of the methods to other areas of science and engineering can be explored, especially for higher spatial dimensions.

This work is supported by the Department of Mathematics and Statistics at the University of Vermont.

No conflict of interest.