Mathematical Analysis of Quasi-Steady State in Droplet Combustion Under Microgravity

Introduction

Combustion modeling offers important theoretical insights and has practical uses in several industries. Spray combustion is widely used in transportation and energy sectors, so the study of liquid fuel droplet combustion is of particular interest. One simplification in the research is the assumption of spherical symmetry in which only one spatial dimension enters the description of the combustion process (see for examples [1-4]). Recent experiments (flame extinguishment (FLEX) experiments) aboard the International Space Station (ISS) utilize a microgravity environment, in which fuel droplets and flames are spherical, to study isolated normal alkane fuel droplet combustion. Combustion experiments with n-heptane fuel yield observations of droplets initially burning with typical “hot flame” behavior, followed by death of the visible flame with continued vigorous vaporization before extinction at a finite droplet radius. It has been hypothesized that the continued vaporization without a visible flame is a second stage of combustion best explained by low temperature, “cool flame” chemistry, suggesting for the first time the existence of dual modes of combustion for pure fuel droplets (see [5-8]).

Attempts to numerically simulate these experimental observations have applied transient sphero-symmetric models with detailed chemical kinetics to study two-stage combustion in pure n-alkane fuel droplets [9-11]. They find that two-stage burning is governed by the balance between diffusive heat-loss and heat generation rates. The effects of environmental parameters (oxygen concentration, diluents), initial droplet diameter, initiall droplet temperature, and ambient pressure are expected to affect the balance between heat loss and generation, either promoting or obstructing the emergence of “cool flame” behavior [9]. The numerical study carried out in [10] identifies the conditions under which it is possible for a “cool flame” to spontaneously reignite into a “hot flame”. Emergence of oscillatory behavior, in which a droplet cycles between the two modes, is reported in [11].

Computational studies of steady-state conservation equations, rather than transient models, demonstrate the existence of quasisteady cool flame droplet combustion regimes and identify the parametric region in which they are possible [12]. A large multistep chemical-kinetic mechanism used in [12] predicts leakage of fuel and oxidizer through the flame during second stage “cool flame” combustion, which could explain the experimentally observed vapor cloud that forms after extinction of the visible flame. Since this behavior closely resembles the “partial burning regime” described in [10], analytical studies have employed it in steady state models for “cool flame” combustion of isolated fuel droplets [13-15].

Partial-Burning Regime for Quasi-Steady State

We now provide a more detailed description of the partial burning regime of the droplet combustion, in particular, the mechanism of the observed “cool flame”. As mentioned earlier, experiments on the ISS have observed two-stage combustion for normal alkane fuel droplets, where an initial hot-flame stage is followed by quasi-steady combustion described by cool-flame kinetics [6]. Since a diffusion flame model is used when separate fuel and oxidizer streams come together through diffusion, the burning rate is dependent upon the rate at which the fuel and oxidizer mix in an appropriate ratio. Until recently, cool-flame chemistry was not thought to be applicable to diffusion flames.

Using asymptotic analysis, Linan shows in [14] the existence of four burning regimes for steady state diffusion flames in a model with spatial domain (-∞,∞). The partial burning regime describes a reaction with frozen flow regions on either side of a thin reaction region where both reactants leak through the flame. It is shown in [12] that fuel vapor and oxygen can leak through the flame in the type of cool-flame droplet combustion considered here. The work in [15] focuses on the partial burning regime of droplet combustion for normal-alkane fuels where the (radial) spatial domain is [0,∞). Like other studies (e.g., [12-14]), several assumptions are made in [15] to simplify the mathematical model. These include spherical symmetry, quasi-steady state burning, uniform droplet temperature, constant product parameters, and the Lewis number being unity. With the introduction of a mixture fraction Z as well as a scaled radial coordinate

, the conservation equations are reduced so that the reactions are confined to a narrow sheet located at Z = Zb and, on either side of this sheet, the reactions are frozen. The temperature profile for Z < Zb, in the frozen region prior to the reaction front, is

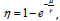
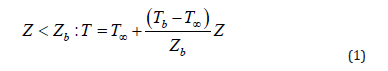
The temperature profile for Z > Z_b is an adjustment to equation (14) in [14]. From [14], β=(T_∞−T_−∞), but in the work of [15], T_−∞ is taken to be the temperature at the center of the droplet, denoted as T₁. The derivation of the temperature profile from the construction in [14] is shown below.

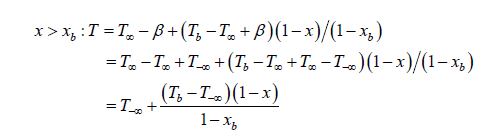
With T_−∞ =T₁ , x = Z, and x_b = Z_b, the temperature profile in frozen flow regions posterior to the flame is given in [15] as

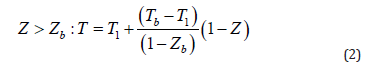
Notice that from (1) and (2) above, the temperature T is a piecewise linear function of Z.

Linan shows in [14] that the temperature distribution in the outer frozen flow regions on either side of the flame should decrease at the same rate. Equating the magnitudes of the slope on either side of the reaction produces a relationship between the unknown Z_b and T_b, the mixture fraction and temperature at the location of the flame, respectively:

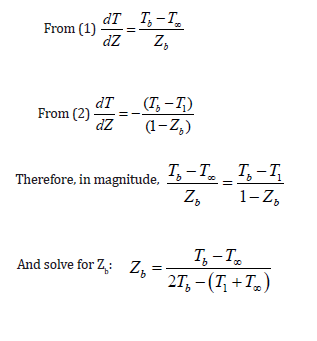
Based on these results, burning rate constant and flame standoff ratio can be derived. First, to satisfy energy conservation, the temperature at the center of the droplet should be defined as the difference between the temperature at the droplet surface and the heat loss with decreasing distance from the center of the droplet. To see that, we start with the boundary conditions at the droplet-gas interface, where η = η_ℓ:

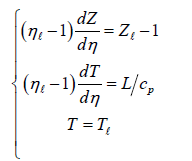
Thus, the slope of the linear function T in Z for Z>Zb is

. Now, by equating slopes: , T1 is solved as .

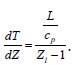
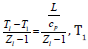
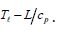
To derive the dimensionless mass burning rate, the scaled radial coordinate η is evaluated at the droplet surface to find the following expression:

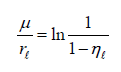
From the post-burn temperature profile given earlier in (2) and the solution to the mixture fraction η=Z the following equation holds:

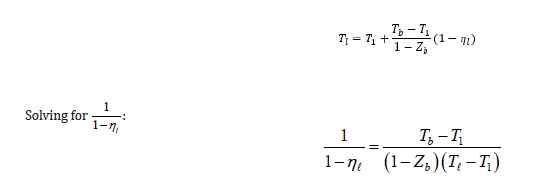
Defining T_v=(T_l-T₁), the dimensionless mass-burning rate is given by:

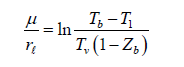
Using the expressions of Z_b and T₁ given earlier, this reduces to

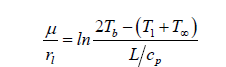
The expression for the burning rate constant,

, becomes

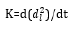
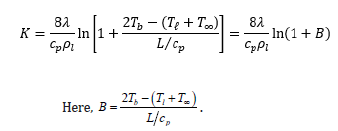
Next, from the definition of η and the fact that η_b = Z_b, η_ℓ = Z_ℓ, the following equations hold:

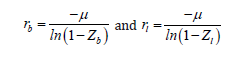
Therefore, the flame-standoff ratio is:

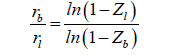
This describes the position of the flame-front compared to the position of the gas-droplet interface. From here, the slope of the temperature profile at Z_b must equal to that at Z_l, i.e.,

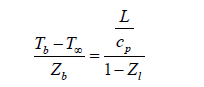
Using the formula for Z_b presented earlier and solving for 1-Z_l:

Comparing this with the definition of B and noting

the following holds

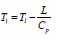
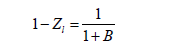
With a similar treatment on 1-Z_b, the final expression for flame standoff ratio is given by

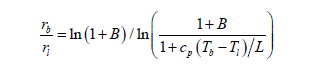
Conclusion

Using the asymptotic results in [14], quasi-steady flame structure including temperature, burning rate, and flame standoff ratio is derived. The predicted flame standoff ratios are compared to numerical investigations from [9] as well as data from the ISS. Both comparisons show impressive agreement between predicted and measured values. New photo technology on the ISS allows for more accurate images of “cool flames”. These are used to calculate a flame-standoff ratio which compares very well with the value predicted by the analyses. All these results further support the partial-burning regime as a reasonable model for cool-flame combustion.

The expressions for burning rate and flame standoff ratio presented here are valid for a specific context. The analysis is applicable to spherical normal-alkane fuel droplets burning in microgravity during the cool-flame stage of combustion which occurs after an initial hot flame. The predictions show promising agreement with experimental results, though some deficiencies in the analyses are identified and suggest the need for further study. For example, the burning rates predicted by the analyses against initial droplet diameter compare well with experimental data. However, the theory predicts that initial droplet diameter has no effect on the burning rate, which is not always observed experimentally. Also, as suggested in [16], pressure dependence on burning rate should be accounted for in the analysis. Both issues warrant further investigation towards a more accurate expression for burning rate of quasi-steady cool flame combustion.

Acknowledgement

This work is financially supported by the Vermont-NASA Space Grant Consortium (grant number 80NSSC20M0122).

Conflicts of Interest

No conflict of interest.