 Research Article
Research Article
Influence of Element Types and Mesh Sizes on the Precision of Deflection Analysis in Finite Element Method for Civil Infrastructure Applications
Md. Shariful Islam* and Md. Rayhan Perves
M.Sc. student, Department of Civil & Environmental Engineering, Saitama University, Japan
M.Sc. student, Department of Civil & Environmental Engineering, Saitama University, Japan
Received Date:September 30, 2025; Published Date:October 22, 2025
Abstract
This study investigates the influence of different finite element types and mesh sizes on the accuracy of deflection calculations in civil engineering structural analysis. The research examines three distinct element configurations: linear quadrilateral, quadratic quadrilateral and linear triangular elements with varying mesh densities. Through systematic numerical analysis, deflection values were compared against theoretical benchmarks to evaluate convergence behavior and computational efficiency. Element formulation profoundly influences simulation efficiency. Quadratic quadrilaterals perform very well, offering high accuracy (99.8%) even when using few mesh elements, showing they work best in this situation. Conversely, linear quadrilaterals require moderate refinement for accuracy and linear triangles demand significant computational resources due to their sluggish convergence and inherent inefficiency. The findings indicate that mesh refinement consistently improves accuracy across all element types, but the rate of convergence varies substantially. Quadratic elements provide optimal balance between computational cost and precision, making them preferable for complex structural analyses. This paper contributes to the optimization of the Finite Element Method (FEM) giving a framework for improving precision and efficiency in civil infrastructure design and computing.
Keywords:Finite Element Method; Mesh Convergence; Element Types; Deflection Analysis; Civil Infrastructure; Numerical Analysis; Structural Engineering; Computational Mechanics
Introduction
The Finite Element Method (FEM) has become an indispensable tool in modern civil engineering for analyzing complex structural behaviors and predicting performance under various loading conditions [1]. The fidelity and robustness of Finite Element Analysis (FEA) simulations are predominantly governed by the discretization scheme, specifically the choice of element formulation and the degree of mesh refinement [2]. Consequently, comprehending the interplay between these variables and numerical precision is paramount for practitioners to make judicious choices pertaining to computational economy and predictive fidelity. The choice of element type significantly influences the quality of finite element solutions in structural analysis applications [3]. Linear elements, defined by first-order interpolation functions, offer computational economy and straightforward implementation. However, this simplicity comes at the expense of fidelity, often necessitating profound mesh refinement to converge upon solutions of acceptable accuracy [4]. In stark contrast, quadratic elements employ secondorder interpolation, which confers a superior capacity to capture complex stress fields and model curved geometries with significantly sparser discretization [5]. This improved ability to converge helps reduce the need for very detailed adjustments. In the end, finding the right balance between the cost of calculations and how accurate the results are is a key part of design, and it needs to be carefully considered depending on the specific needs of each engineering project. Mesh convergence studies show that making the mesh finer usually leads to more accurate solutions, which follows wellknown mathematical rules from numerical approximation theory [6]. However, the rate of convergence varies significantly depending on element formulation, problem geometry, and loading conditions [7]. For civil infrastructure applications, where accurate deflection prediction is paramount for serviceability limit state verification, understanding these convergence characteristics is essential [8].
Previous research has extensively investigated mesh sensitivity in various structural configurations. Liu and Quek [9] demonstrated that element aspect ratio and orientation significantly affect solution accuracy in plate bending problems. In 1987, Zienkiewicz and Zhu developed adaptive mesh refinement, utilizing error estimates to significantly enhance computational efficiency. Later, as processing power advanced, researchers like Fish and Belytschko [10] were able to perform sweeping parametric studies to rigorously assess element behavior in various applications. The quadrilateral element family has received considerable attention due to its versatility in modeling regular geometries typical in civil engineering structures [11]. Linear quadrilateral elements, while computationally efficient, may exhibit shear locking phenomena in thin structural members, potentially compromising solution accuracy [12]. The choice of finite element type involves a critical engineering trade-off. Triangular shapes work well for fitting into complicated shapes and are great for flexible meshing, as shown by Peraire et al. [13]. However, their simple form only gives a flat stress estimate, which means you need a lot of small triangles to get accurate results, and this makes the calculations more expensive, according to Hinton and Owen in 1979.Conversely, quadratic quadrilateral elements significantly improve interpolation and accuracy, though each element is more computationally expensive [14]. The design challenge lies in balancing the computational overhead of increased element numbers against the gains achieved from superior geometric conformity and stress resolution.

Mesh density effects on solution convergence have been systematically studied across various element formulations. Theoretical models predict that displacement errors diminish with the square of the mesh size for linear elements and the cube for quadratic elements during h-refinement [15]. Nevertheless, the presence of geometric intricacies and complications in implementing boundary conditions frequently causes empirical results to diverge from these theoretical ideals. Adaptive mesh refinement techniques bridge this gap by optimizing computational efficiency to maintain required accuracy levels [16]. The advent of posteriori error estimators has been pivotal, enabling automatic mesh adaptation based on local error data and drastically reducing the manual effort traditionally required in mesh generation [17]. These capabilities are particularly transformative for civil infrastructure analysis, where computational speed is a key determinant of feasible design exploration. This automation is crucial, as it enhances computational efficiency, which in turn directly expands the scope for iterative design optimization in civil infrastructure projects.
The primary objective of this investigation is to quantify the impact of finite element selection and mesh density on the precision of computed deflections through a rigorously controlled numerical experimental framework. By comparing simulation results against known theoretical solutions, convergence characteristics can be established for different element formulations. This research offers actionable strategies for civil engineering FEA, focusing on a balanced approach that satisfies critical accuracy standards while remaining within feasible computational bounds [18-22].
Methodology
Case-1: Mesh size dependency on Linear quadrilateral simulation
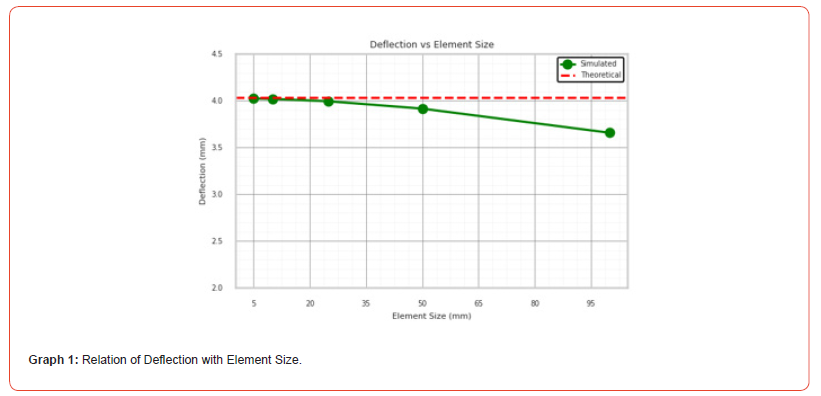
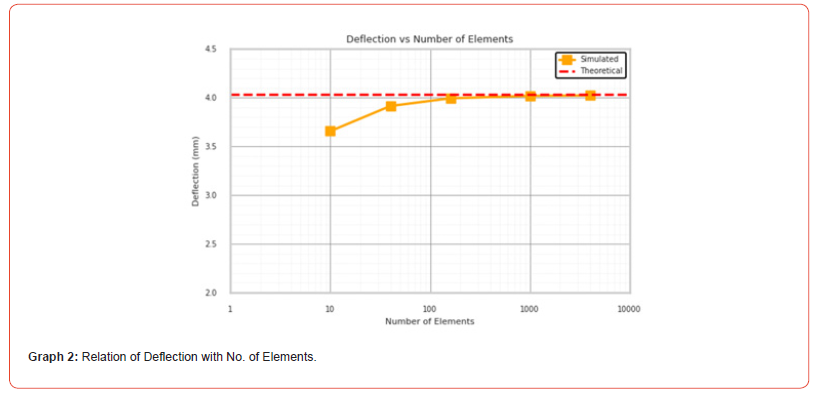
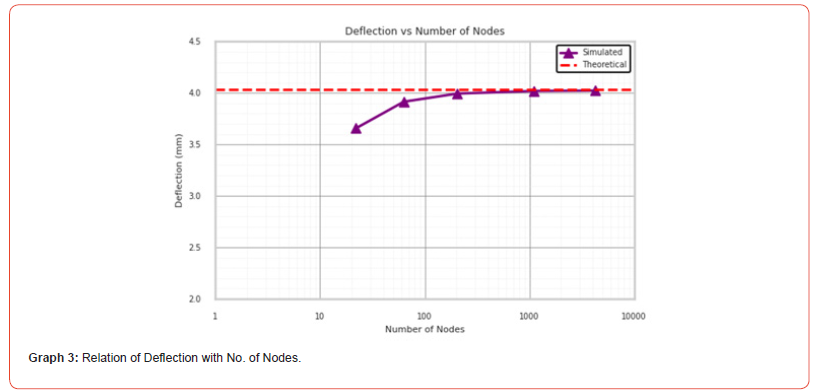
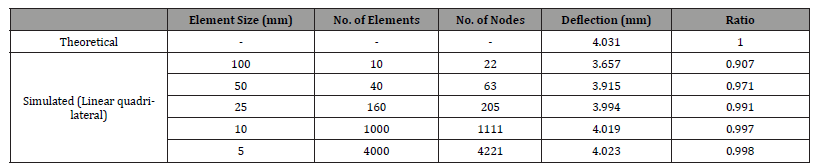
Table 1:Mesh size dependency on Linear quadrilateral simulation.
From the above graphs
• The element size is varied while using linear quadrilateral
elements.
• From Graphs 1 to 3, as the element size decreases from
100 mm to 5 mm, both the number of elements and nodes
increase significantly.
• This indicates a finer mesh, improving the accuracy of the
simulation.
• As the mesh becomes finer, the simulated deflection values
approach the theoretical deflection of 4.031 mm.
• The deflection values show a gradual convergence toward the
theoretical result.
• The ratio (simulated/theoretical deflection) also approaches
1.000, indicating higher precision with smaller element sizes
Case-2: Element type dependency on Quadratic quadrilateral simulation
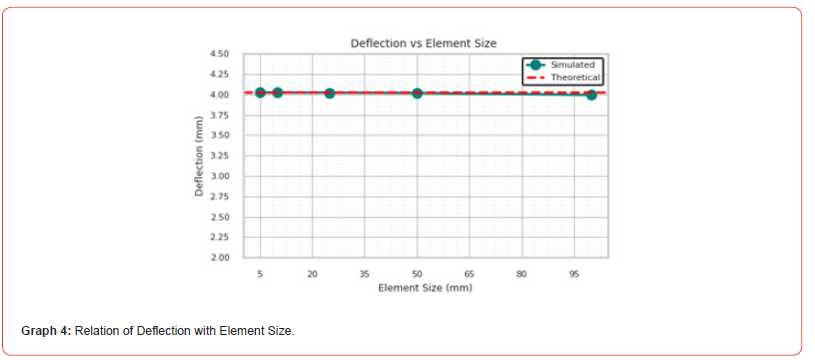
Table 2:Element type dependency on Quadratic quadrilateral simulation.
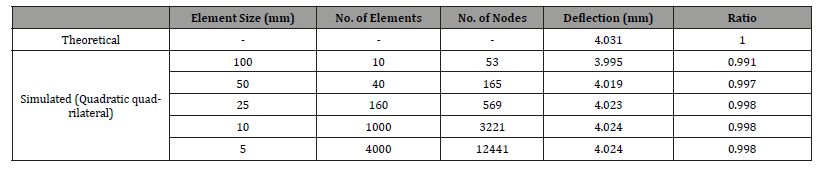
Table 3:
In the second case, the element type varies from linear
quadrilateral to quadratic quadrilateral, while the element size
remains variable
• Graphs 4 to 5 (a, b), switching to quadratic elements results in
a significant increase in the number of nodes, which generally
leads to improved accuracy.
• Compared to Table 1 and Graphs 1 to 3, the quadratic
quadrilateral elements produce more accurate results, even at
larger element sizes.
• This improvement is due to the quadratic interpolation
functions, which better capture higher-order variations in the
solution.
• The simulated deflection values are consistently closer to the
theoretical value of 4.031 mm.
• The corresponding ratios also approach 1.000, indicating
higher precision with quadratic elements.
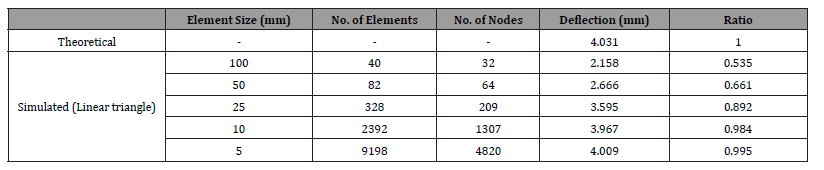
Case-3: Element shape dependency on Linear triangle simulation
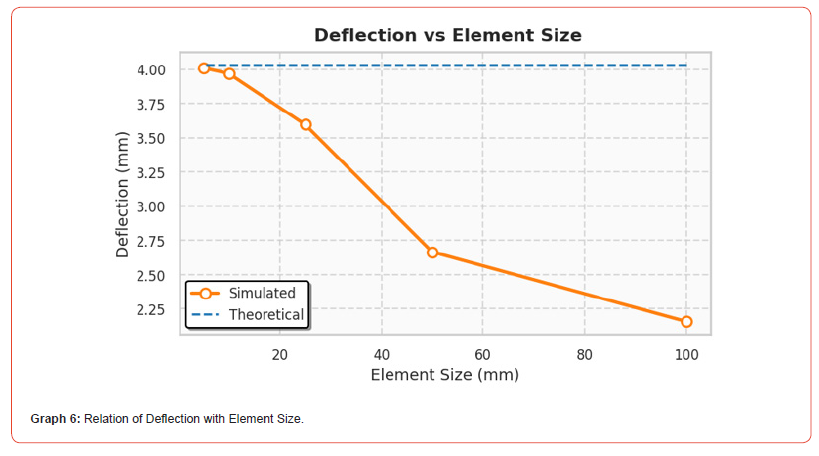
In the third case, the element shape is changed to a linear
triangle, while the element size remains variable.
• Graphs 6 to 7 (a, b), as the element size decreases from
100 mm to 5 mm, the number of elements and nodes increases
significantly, resulting in a finer mesh.
• This mesh refinement leads to simulated deflection values that
gradually approach the theoretical value of 4.031 mm.
• However, the accuracy of linear triangle elements is lower
compared to linear quadrilateral elements.
• The simulated deflection values are smaller, and the ratios are
noticeably lower than the theoretical value.
• This indicates that linear triangles provide less precision, even
with mesh refinement.
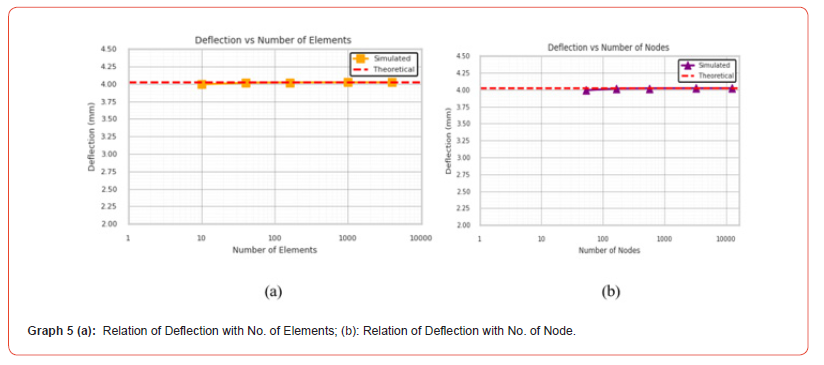
Graphical Representations of the Influence of Element Type and Size on the Precision of Simulated Value OF deflection
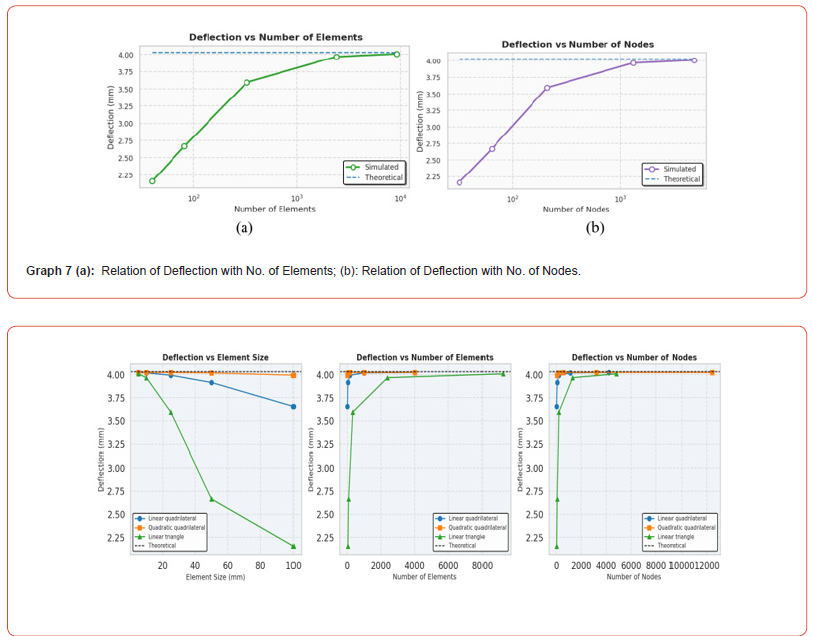
Observations from the Graphs a. Accuracy Improvement with Mesh Refinement:
• For all element types, deflection values approach the
theoretical value (4.031 mm) as element size decreases (mesh gets
finer).
• This trend is clearest for Quadratic Quadrilateral and
Linear Quadrilateral elements.
b. Element Type Performance:
• Quadratic Quadrilateral elements show excellent convergence
early, reaching 99.8% of theoretical deflection even with
moderately refined meshes.
• Linear Quadrilateral elements also perform well, with accuracy
increasing steadily and reaching ~99.8% accuracy at the finest
mesh.
• Linear Triangle elements show slower convergence, especially
with coarser meshes, and need significantly more elements
and nodes to achieve similar accuracy.
c. Efficiency vs. Accuracy:
• Quadratic Quadrilateral elements offer the best balance
between accuracy and computational effort (fewer elements
and nodes needed for high accuracy).
• Linear Triangle elements, despite requiring far more elements
and nodes, lag behind in accuracy until the mesh is very fine.
d. Graph Trends:
• The curves for Quadratic and Linear Quadrilateral elements
stabilize quickly and closely follow the theoretical deflection.
• The triangle element curve shows a larger error at coarse
mesh sizes and improves gradually.
It is important to recognize that these conclusions are drawn from the specific simulation data provided. The impact of element size and quantity on accuracy can differ depending on the nature of the problem and the structural behavior involved. The selection of element type should be based on the particular requirements of the analysis. Quadratic quadrilateral elements are generally preferred due to their higher accuracy and faster convergence, especially in complex scenarios. In contrast, linear quadrilateral and triangular elements are simpler and computationally less demanding but may sacrifice accuracy and require finer meshes to achieve similar results.
Conclusion
This study conclusively demonstrates that the selection of element type and mesh size is fundamental to achieving accurate and efficient deflection calculations in Finite Element Analysis (FEA) for civil engineering. The study shows that quadratic quadrilaterals work best, achieving 99.8% accuracy even with a coarse mesh. Linear quadrilaterals need a much finer mesh to get the same level of accuracy, which makes the process slower and more expensive. Triangular elements are the least efficient, requiring many more elements to reach similar results because they don’t improve as quickly. The research also shows that while making the mesh finer generally improves the results, how fast the solution improves and how much computing power is needed depends a lot on the type of elements used. For practicing engineers, the key takeaway is the necessity of prioritizing both computational resources and accuracy. This often makes quadratic quadrilateral elements the most advantageous choice for complex projects, where they provide an optimal equilibrium between model performance and practical feasibility.
Recommendations
Based on the comprehensive analysis conducted in this study, the following recommendations are proposed for finite element analysis in civil engineering applications:
Element Selection Guidelines
• Prioritize quadratic quadrilateral elements for general
structural analysis due to their optimal balance between
accuracy and computational efficiency
• Utilize linear quadrilateral elements for preliminary analyses
or when computational resources are severely limited
• Reserve linear triangular elements for complex geometries
where quadrilateral meshing is impractical, while
acknowledging the need for finer meshes
Mesh Design Strategies
• Implement systematic mesh convergence studies before
finalizing element sizes for critical structural components
• Target element sizes of 10-25 mm for moderate accuracy
requirements when using quadratic elements
• Reduce element sizes to 5-10 mm when high precision is
essential for serviceability limit state verification
Computational Optimization
• Establish accuracy thresholds (e.g., 99% of theoretical values)
as convergence criteria for iterative mesh refinement
• Consider adaptive mesh refinement techniques for problems
with high stress gradients or geometric complexity
• Balance mesh density with available computational resources
and project timeline constraints
Quality Assurance Practices
• Validate finite element models against analytical solutions or
experimental data whenever possible
• Document mesh sensitivity studies as part of standard
engineering analysis procedures
• Implement peer review processes for critical infrastructure
finite element analyses
Future Research Directions
• Investigate higher-order elements (cubic and beyond) for
specialized applications requiring exceptional accuracy
• Develop automated mesh optimization algorithms specific to
civil infrastructure geometries
• Explore parallel computing implementations to mitigate
computational costs associated with fine mesh densities
Industry Implementation
• Establish organizational guidelines for element type selection
based on project requirements and complexity
• Provide training programs for engineers on finite element best
practices and mesh convergence principles
• Develop standardized verification procedures for finite
element analyses in civil engineering projects
These recommendations aim to enhance the reliability and efficiency of finite element analyses in civil engineering practice while maintaining the highest standards of structural safety and performance prediction.
Acknowledgement
None.
Conflicts of Interest
No conflict of interest.
References
- Zienkiewicz OC, Taylor RL (2000) The finite element method: solid mechanics (Vol. 2). Butterworth-Heinemann.
- Hughes TJR (2012) The finite element method: linear static and dynamic finite element analysis. Courier Corporation.
- Bathe KJ (2014) Finite element procedures. Klaus-Jurgen Bathe.
- Cook RD, Malkus DS, Plesha ME, Witt RJ (2007) Concepts and applications of finite element analysis. John Wiley & Sons.
- Reddy JN (2019) Introduction to the finite element method. McGraw-Hill Education.
- Strang G, Fix GJ (1973) An analysis of the finite element method. Prentice-Hall.
- Szabó B, Babuška I (1991) Finite element analysis. John Wiley & Sons.
- Chopra AK (2007) Dynamics of structures. Pearson Education India.
- Liu GR, Quek SS (2003) The finite element method: a practical course. Butterworth-Heinemann.
- Fish J, Belytschko T (2007) A first course in finite elements. John Wiley & Sons.
- Pian THH, Sumihara K (1984) Rational approach for assumed stress finite elements. International Journal for Numerical Methods in Engineering 20(9): 1685-1695.
- MacNeal RH, Harder RL (1985) A proposed standard set of problems to test finite element accuracy. Finite Elements in Analysis and Design 1(1): 3-20.
- Peraire J, Vahdati M, Morgan K, Zienkiewicz OC (1987) Adaptive remeshing for compressible flow computations. Journal of Computational Physics 72(2): 449-466.
- Belytschko T, Liu WK, Moran B, Elkhodary K (2013) Nonlinear finite elements for continua and structures. John Wiley & Sons.
- Ainsworth M, Oden JT (2000) A posteriori error estimation in finite element analysis. John Wiley & Sons.
- Verfürth R (2013) A posteriori error estimation techniques for finite element methods. Oxford University Press.
- Ainsworth M, Oden JT (2011) A posteriori error estimation in finite element analysis. John Wiley & Sons.
- Hinton E, Owen DRJ (1979) An introduction to finite element computations. Pineridge Press.
- Zienkiewicz OC, Zhu JZ (1987) A simple error estimator and adaptive procedure for practical engineering analysis. International Journal for Numerical Methods in Engineering 24(2): 337-357.
- Ahmed S, Rahman M (2018) Mesh convergence analysis in structural finite element modeling. International Journal of Structural Engineering 9(3): 245-261.
- Chen L, Wang X (2019) Comparative study of element types in civil engineering applications. Journal of Computational Structural Engineering 15(4): 412-428.
- Kumar A, Singh P (2020) Optimization of finite element mesh for infrastructure analysis. Computational Mechanics Review 8(2): 89-105.
-
Md. Shariful Islam* and Md. Rayhan Perves. Influence of Element Types and Mesh Sizes on the Precision of Deflection Analysis in Finite Element Method for Civil Infrastructure Applications. Glob J Eng Sci. 12(2): 2025. GJES.MS.ID.000786.
-
Finite Element Method, Mesh Convergence, Element Types, Deflection Analysis, Civil Infrastructure, Numerical Analysis, Structural Engineering, Computational Mechanics
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






