 Research Article
Research Article
Analysis of the Wave Solutions of the Nonlinear Evolution Equations Help of Advanced -Expansion Scheme
Loskar Nowsher Ali and Md Habibul Bashar*
Department of Mathematics, European University of Bangladesh, Dhaka-1216, Bangladesh
Md Habibul Bashar, Department of Mathematics, European University of Bangladesh, Dhaka-1216, Bangladesh.
Received Date:January 30, 2023; Published Date:February 10, 2023
Abstract
With the assistance of emblematic calculation programming, the current paper explores the specific voyaging wave arrangements from the general (2+1)- layered nonlinear development conditions by utilizing the advanced
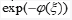
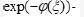
Keywords:Time fractional derivative; The advanced
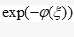
Introduction
As of late, nonlinear halfway differential conditions (NPDEs) is extensively used to portray various critical marvels and dynamic techniques in various areas of science and designing, particularly in liquid mechanics, hydrodynamics, numerical science, dispersion process, strong state physical science, plasma physical science, brain physical science, substance energy and geo-optical filaments.
In this work, we will study the summed up (2+ 1) layered nonlinear advancement conditions in the structure.
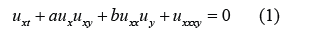
Recently, some special cases of Eq. (1) have been studied by several authors [1-4]. When setting a =4 and b = 2, Eq. (1) becomes the (2+1)-dimensional Calogero–Bogoyavlenskii–Schiff (CBS) equation:
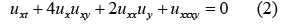
When setting a = – 4 and b = – 2, Eq. (1) becomes the (2+1)-dimensional breaking soliton equation
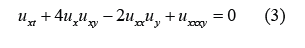
When setting a = 4 and b = 4, Eq. (1) becomes the (2+1)-dimensional Bogoyavlenskii’s breaking soliton equation:
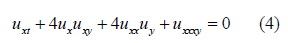
Numerous researchers arranged through NEEs to develop voyaging wave arrangement by carry out a few techniques. The strategies that are deep rooted in late writing, for example, the drawn out Kudryashov strategy [5], the changed basic condition technique [6], the new broadened (G’/G) development strategy [7,8], the Darboux change [9], the preliminary arrangement technique [10], the Exp-Capability Strategy [11], the numerous least difficult condition technique [12], exp(−ϕ (ξ )) - extension strategy [13-17], Pseudo illustrative model [18-20], etc.
The objective of this article is to apply the high level exp(−ϕ (ξ )) - development technique [21] to construct the exact journeying wave deals with any consequences regarding nonlinear headway conditions in logical material science through the time partial nonlinear changed Kawahara conditions.
The article is set up as seeks after: In segment 2, the high level exp(−ϕ (ξ )) - extension procedure has been discussed. In segment 3, we apply this plan to the nonlinear advancement conditions raised previously. In segment 4, addresses Results and Conversation and In area 5, closes are given.
Preliminaries and Methods
Definition and some features of conformable fractional derivative
The conformable fractional derivative with a limit operator which was initially introduced by Khalil et al. [22].
Definition: f : (0,∞)→ , then, the conformable fractional derivative of f order α is defined as
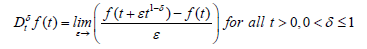
Later, Abdeljawad [23] has also offered chain rule, exponential functions, Gronwalls inequality, integration by parts, Taylor power series expansions and Laplace transform for conformable derivative in fractional versions. The definition of conformable fractional derivative can easily overcome the difficulties of exiting modified Riemann-Liouville derivative definition [24].
a. Theorem 1: Let δ ∈(0,1] and f=f(t), g=g(t) be α-conformable differentiable at a point t>0 then:
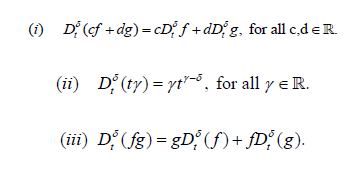
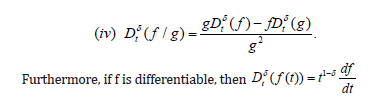
b. Theorem 2: Let f : (0,∝)→ R be a function such that f is differentiable and α-conformable differentiable. Also, let be a differentiable function defined in the range of f. Then
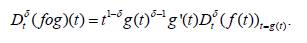
Where, prime denotes the classical derivatives with respect to t.
The advancedexp(−ϕ (ξ )) -expansion method
In this section, we will précis exp(−ϕ (ξ )) -expansion method step by step. Consider a nonlinear partial differential equation in the following form,
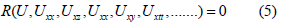
Where U = U(x, y, z, t) is an unknown function, R is a polynomial of U , its different type partial derivatives, in which the nonlinear terms and the highest order derivatives are involved.
a. Step-1: Now we consider a transformation variable to convert all independent variable into one variable, such as
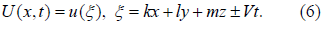
By implementing this variable Eq. (6) permits us reducing Eq. (5) in an ODE for u(x,t)= u(ξ )
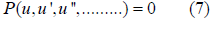
b. Step-2: Suppose that the solution of ODE Eq. (7) can be expressed by a polynomial in exp(−ϕ (ξ )) as follows
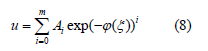
where the derivative of ϕ (ξ ) satisfies the ODE in the following form
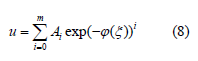
then the solutions of ODE Eq. (9) are Case I: Hyperbolic function solution (when λμ < 0 ):
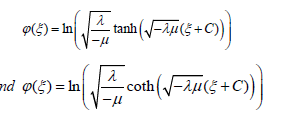
Case II: Trigonometric function solution (when λμ > 0):
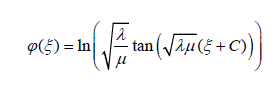
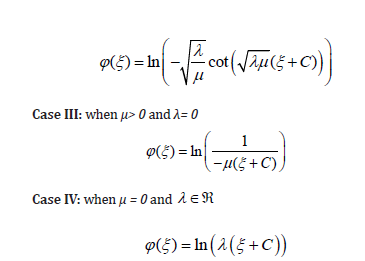
Where C is integrating constants and λμ< 0 or λμ> 0 depends on sign of μ.
c. Step-3: By substituting Eq. (8) into Eq.(7) and using the ODE (9), collecting all same order of exp(−ϕ (ξ )) together, then we execute an polynomial form of exp(−ϕ (ξ )) . Equating each coefficients of this polynomial to zero, yields a set of algebraic system.
d. Step-4: Assume the estimation of the constants can be gotten by fathoming the mathematical conditions got in step 4. Substituting the estimations of the constants together with the arrangements of Eq. (9), we will acquire new and far reaching precise traveling wave arrangements of the nonlinear development Eq. (5).
Application of the Method
In this sub section, we will exert the advanced exp(−ϕ (ξ )) -expansion strategy to solve the equation (1). Now Using the traveling wave variable
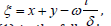
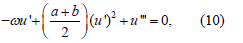
Where, primes denote the differentiation with regard to ξ. By balancing u’’’ and (u’)2, we obtain N = 1. Therefore, the advanced exp(−ϕ (ξ )) -expansion admits to solution of (8) in the form
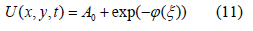
Now, substituting Eq. (11) into Eq. (10), and equating the coefficients of the powers ϕ (ξ ) then we obtain a system of algebraic equations. Solving this system of equations for A0,A1 and ω, we obtain the following values:
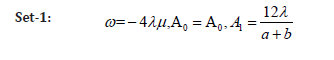
a. Case-I: When λμ < 0 we get following hyperbolic solution Family-1
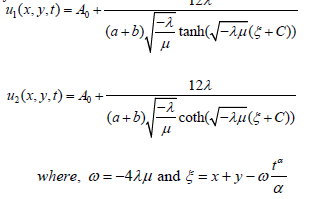
b. Case-II: When λμ > 0 we get following trigonometric solution Family-2
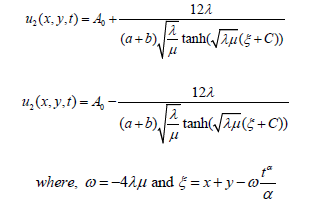
c. Case III: When λ = 0 the executing value of A1 = 0. So, the solution cannot be obtained. For this purpose, this case is rejected. d. Case IV:
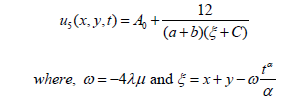
Results and Discussion
Around here, we will discuss the actual depiction of the obtained accurate and singular wave answer for the general (2+1)- layered nonlinear advancement condition. We address these arrangements in graphical and actually take a look at about the kind of arrangement. Presently we pictorial some get arrangements acknowledge by applied techniques for the general (2+1)- layered nonlinear development condition (Figures 1-4).
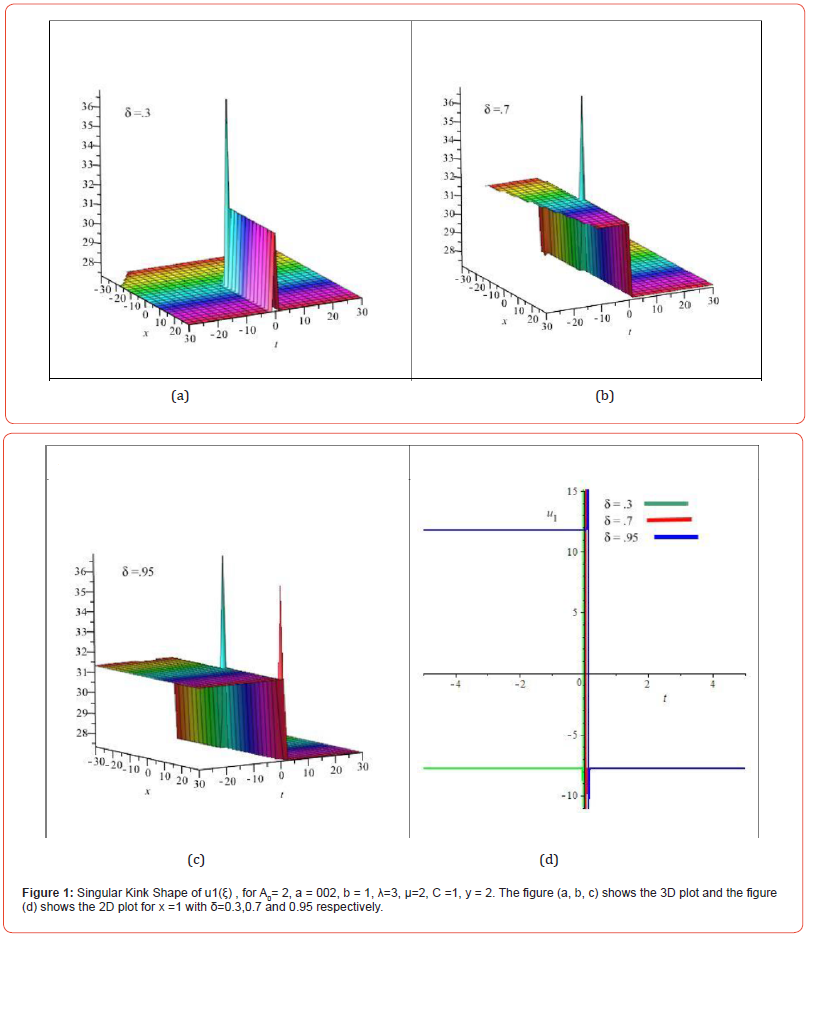


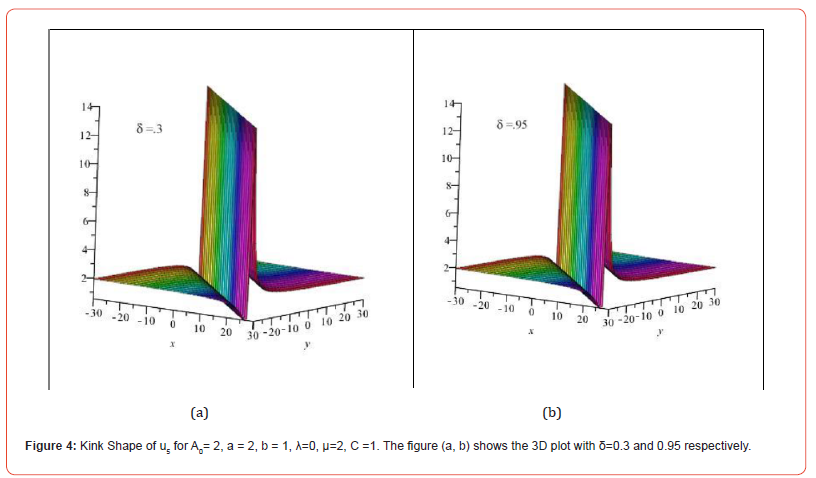
Conclusion
In this portion, we have seen that two sorts of voyaging wave game plans similar to exaggerated and mathematical capacities with regards to the general (2+1)- layered nonlinear development condition is really found by using the high level exp(−ϕ (ξ )) - extension technique. From our results got in this paper, we wrap up the high level exp(−ϕ (ξ )) - development plot procedure is astonishing, strong and accommodating. The show of this strategy is reliable, essential and gives various new plans. The high level exp(−ϕ (ξ )) - development strategy enjoys more benefits: It is immediate and compact. Moreover, the courses of action of the proposed nonlinear improvement conditions in this paper have various expected applications in nuclear and particle material science. Finally, this procedure gives a momentous logical instrument to get progressively wide precise game plans of an enormous number of nonlinear PDEs in mathematical material science.
Acknowledgement
None.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding this paper.
References
- Al-Amr MO (2015) Exact solutions of the generalized (2+1)-dimensional nonlinear evolution equations via the modified simple equation method. Comput Math Appl 69(5): 390-397.
- Najafi M, Najafi M, Arbabi S (2013) New Exact Solutions for the Generalized (2+1)-dimensional Nonlinear Evolution Equations by Tanh-Coth Method. Int J Modern Theoretical Phys 2(2): 79-85.
- Najafi M, Arbabi S, Najafi M (2013) New application of sine-cosine method for the generalized (2+1) dimensional nonlinear evolution equations. Int J Adv Math Sci 1(2): 45-49.
- Darvishi MT, Najafi M, Najafi M (2010) New application of EHTA for the generalized (2+ 1)-dimensional nonlinear evolution equations. Int J Math Comp Sci 6(3): 132-138.
- Emrullah Yasar, Yakup Yildırım, Abdullahi Rashid Adem (2018) Perturbed optical solitons with spatio-temporal dispersion in (2 + 1)-dimensions by extended Kudryashov method Optik 158: 1–14.
- Harun-Or Roshid, Md. Mamunur Roshid, Nizhum Rahman, Razia Pervin (2017) New solitary wave in shallow water, plasma and ion acoustic plasma via the GZK-BBM equation and the RLW equation, Propulsion and Power Research 6(1): 49–57.
- HO Roshid, MF Hoque, MA Akbar (2014) New extended (G’/G)-expansion method for traveling wave solutions of nonlinear partial differential equations (NPDEs) in mathematical physics, Italian. J Pure Appl Math 33: 175-190.
- LL Feng, TT Zhang (2018) Breather wave, rogue wave and solitary wave solutions of a coupled nonlinear Schrodinger equation, Appl Math Lett 78: 133-140.
- Xu Shuwei, He Jingsong (2012) The rogue wave and breather solution of the Gerdjikov-Ivanov equation, Journal of Mathematical Physics 53.
- A Biswas, M Mirzazadeh, M Eslami, Q Zhou, A Bhrawy, et al. (2016) Optical solitons in nano-fibers with spatio-temporal dispersion by trial solution method, Optik 127(18): 7250–7257.
- Jalil Manafian Heris, Isa Zamanpour (2013) Analytical treatment of the Coupled Higgs Equation and the Maccari System via Exp-Function Method 33: 203-216.
- YM Zhao (2014) New Exact Solutions for a Higher-Order Wave Equation of KdV Type Using the Multiple Simplest Equation Method, Journal of Applied Mathematics, pp. 1-13.
- Rafiqul Islam, Harun-Or-Roshid (2017) Application of -expansion method for Tzitzeica type nonlinear evolution equations, Journal for Foundations and Applications of Physics 4(1).
- N Rahman, S Akter, HO Roshid, MN Alam (2014) Traveling Wave Solutions of The (1+1)-Dimensional Compound KdVB equation by –Expansion Method, Global Journal of Science Frontier Research 13(8): 7-13.
- R Islam, MN Alam, AKMKS Hossain, HO Roshid, MA Akbar (2014) Traveling wave solutions of nonlinear evolution equations via -expansion method, Global Journal of Scientific Frontier Research 13(11): 63-71.
- N Kadkhoda, H Jafari (2017) Analytical solutions of the Gerdjikov–Ivanov equation by using expansion method, Optik 139: 72–76.
- Amfilokhiev VB, Voitkunskii YI, Mazaeva NP, Khodorkovskii YS (1975) Flows of polymer solutions in the case of convective accelerations Tr. Leningr. Korablestroit Inst 96: 3-9.
- Mamunur Roshid, Harun-Or Roshid (2018) Exact and explicit traveling wave solutions to two nonlinear evolution equations which describe incompressible viscoelastic Kelvin-Voigt fluid, Heliyon 4.
- Omer Faruk Gozukizil, Samil Akcagil (2013) The tanh-coth method for some nonlinear pseudoparabolic equations with exact solutions, Advances in Difference Equations, 143p.
- Ak Turgut, Tugba Aydemir, Asit Saha, Abdul Hamid Kara (2018) Propagation of nonlinear shock waves for the generalised Oskolkov equation and its dynamic motions in the presence of an external periodic perturbation, Pramana – J Phys, pp. 78-90.
- Rahhman MM, Aktar A, Roy KC (2018) Analytical Solutions of Nonlinear Coupled Schrodinger–KdV Equation via Advance Exponential Expansion. American Journal of Mathematical and Computer Modelling 3(3): 46-51.
- R Khalil, M Al Horani, A Yousef, M Sababheh (2014) A new definition of fractional derivative. J Comput Appl Math 264: 65–70.
- Abdeljawad T (2015) On conformable fractional calculus. J Comput Appl Math 279: 57–69.
- G Jumarie (2006) Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput Math Appl 51(9): 1367 – 1376.
-
Loskar Nowsher Ali and Md Habibul Bashar*. Analysis of the Wave Solutions of the Nonlinear Evolution Equations Help of Advanced -Expansion Scheme. Glob J Eng Sci. 10(5): 2023. GJES.MS.ID.000749
-
Time fractional derivative, The advanced -expansion method, Exact solution, The general ( 2+1)-dimensional nonlinear evolution equation, Mathematical physics
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






