 Research Article
Research Article
Thermodynamically Consistent Models of Elastic-Plastic Materials
Claudio Giorgi1 and Angelo Morro2*
1DICATAM, Universita` di Brescia, Via Valotti 9, 25133 Brescia, Italy
2DIBRIS, Universita` di Genova, Via all’Opera Pia 13, 16145 Genova, Italy
Angelo Morro, DIBRIS, Universita` di Genova, Via all’Opera Pia 13, 16145 Genova, Italy.
Received Date: July 19, 2021; Published Date: August 05, 2021
Abstract
A three-dimensional thermodynamic setting for the modelling of elastic-plastic materials is established. The second law of thermodynamics is assumed in the Clausius-Duhem form with the entropy production being given by a constitutive function. An incremental stress strain relation is derived. In essence the free energy is found to describe the elastic behaviour while the hysteretic properties are a joint consequence of the entropy production and the free energy.
Introduction
The purpose of this paper is to establish a thermodynamic three-dimensional setting for the modelling of thermo-elastic-plastic properties of solids. To this end we follow the scheme of rational thermodynamics [1] which is based on the (local) balance equations and the Clausius-Duhem inequality as a way of selecting physically admissible constitutive equations. However, we allow the entropy production too to be given by a constitutive function. This view is quite unusual in the literature and is the key point of the present approach. Mathematically it emerges that new schemes can occur due to common dependences of the free energy, possibly of the stress, and of the entropy production. To describe the elastic- plastic behaviour we consider the stress, the strain, and their rates within the set of independent variables. Here it follows that the dependence of the entropy production on the strain rate or on the stress rate combine with the time derivative of the free energy thus providing relations which are qualitatively new; the free energy is dependent on both stress and strain. These models show a joint occurrence of terms arising from the free energy and terms determined by the entropy production. The flexibility of the models and the thermodynamic consistency are the main advantages of the constitutive property of the entropy production.
Second-Law Inequality and Entropy Production
Consider a continuous body occupying a time-dependent region Ω⊂ε 3 . Any point of the body is labelled by the position X occupied
in a reference configuration R. The motion is described by the
function χ that to each X ∈ R, at time t ∈ ℝ, associates the position
x ∈ Ω. Denote by ∇ and ∇R the gradient with respect to x and X. The
symbol ∂t denotes the time derivative at a point x in space while a
superposed dot denotes the time derivative relative to the observer
following the motion of the point under consideration. Hence for any differentiable function f (t, x) we have 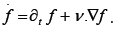 Instead,
if we have g (t, X) then g˙= ∂tg. The body is regarded as a deformable
and heat-conducting solid. The balances of mass and linear momentum
are written in the form
Instead,
if we have g (t, X) then g˙= ∂tg. The body is regarded as a deformable
and heat-conducting solid. The balances of mass and linear momentum
are written in the form
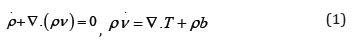
where ρ is the mass density, v is the velocity, T is the symmetric Cauchy stress tensor, b is the body force. The balance of energy is written in the form
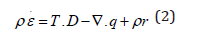
where ε is the internal energy density (per unit mass), D is the stretching tensor, q is the heat flux, and r is the heat supply.
Let η be the entropy density and θ the absolute temperature. The balance of entropy is expressed by saying that there is an entropy flux φ and an entropy supply ρs; here we let φ = q/θ and s = r/θ. The balance is stated by assuming that in any process the entropy rate is greater than what is given by φ and s,
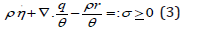
The quantity σ so defined is said to be the entropy production. Substitution of ρr − ∇·q from the balance of energy (2) into (3) results in
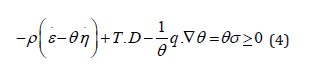
By means of the Helmholtz free energy ψ = ε−θη we obtain from (4) that
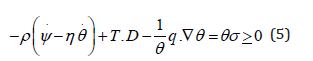
For the present purposes it is convenient to consider (referential) Lagrangian quantities. Let F = ∇R χ be the deformation gradient and J = det F. Hence, we let E = ½ (FT F − 1) and
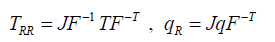
TRR is the second Piola (or Piola-Kirchhoff) stress tensor. It follows that
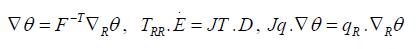
Observe Jρ =ρR is the mass density in R. Multiplying inequality (5) by J we obtain
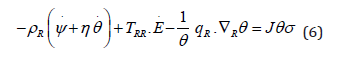
As is standard in continuum mechanics [1,2] we consider any set of constitutive equations as physically admissible if the Clausius- Duhem inequality (5), or (6), holds identically for any process subject to the balance equations (1), (2). Equation (3) defines the value of the entropy production; σ > 0 characterizes dissipative phenomena. About (6), and likewise (5), the constitutive functions for ψ, η, TRR, qR are physically admissible only if the left-hand side is non-negative for any process satisfying eqs. (1), (2). Rather we consider σ too as given by a constitutive function subject to taking non-negative values. Consequently, the constitutive functions ψ, η, TRR, qR, σ are physically admissible if they satisfy identically both conditions
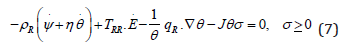
for any process subject to the balance equations. The assumption that the entropy production σ, or the rate of dissipation θσ, be given by a constitutive equation traces back to [3]. Later on, this assumption was used in [4]. Recently we have shown how the constitutive function for σ is essential in the modelling of ferroelectric hysteresis [5,6]. We now show that the constitutive property of the entropy production allows a thermodynamically consistent class of elastic-plastic models.
Stress-Strain Response in Three-Dimensional Plasticity
In plasticity, and likewise in any hysteretic model, the dependence of TRR on E would be given by a multivalued function. To avoid this type of dependence it seems convenient to let the pertinent constitutive equations depend on both stress and strain. Moreover, since we look for rate-type models of the stress-strain relation we let E˙ and T˙RR be among the independent variables. Accordingly, we assume ψ, η, qR, σ are continuous functions of the set of variables
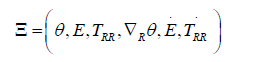
The function ψ is assumed to be continuously differentiable. Upon evaluation of ψ˙ substitution in (6) we find

where the derivatives of ψ, η and σ are continuous functions of Ξ. The linearity and arbitrariness of ∇R θ˙, E¨, T¨RR and θ˙ imply
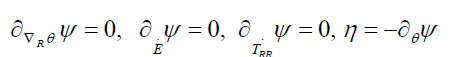
Hence it follows the reduced dissipation inequality
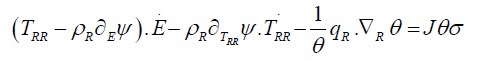
Since ψ is independent of ∇R θ then letting ∇R θ = 0 we have
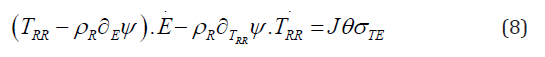
where σTE = σ at ∇R θ = 0 and σTE ≥ 0. Consequently
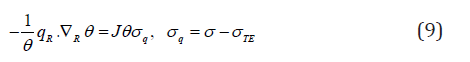
Given a constitutive equation for qR, eq. (9) yields the constitutive function for σq, that is

Equation (8) yields different results depending on the function σTE. Anyway it is worth considering the following
Proposition. Let N be a second-order tensor with |N| = 1. Any second-order tensor Z can be represented in the form
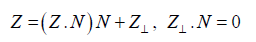
In words, Z is split into the longitudinal part (Z · N) N and the transverse part Z⊥.
We first look at (8) in the case σTE = 0 whence
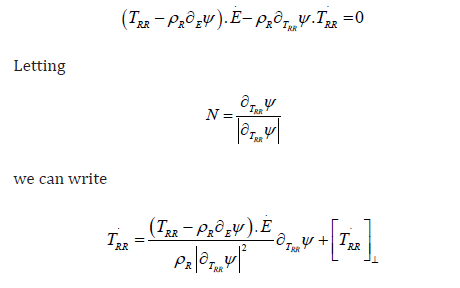
in geometrical words, the thermodynamic restriction (8) determines
the longitudinal part of TRR whereas the transverse part 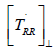 is left undetermined. This result yields infinitely many representations
of.TRR compatible with thermodynamics. If, e.g., we let
is left undetermined. This result yields infinitely many representations
of.TRR compatible with thermodynamics. If, e.g., we let 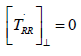 then we find
then we find
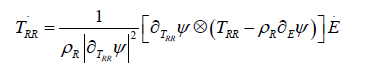
We now let 0 TE σ ≠ . By (8) we have
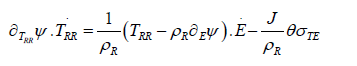
Assume again for simplicity 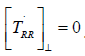 Hence, we find that
Hence, we find that
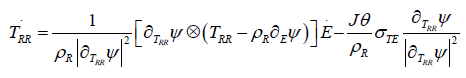
Consequently, the non-zero entropy production σTE results in the additional contribution
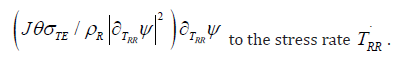
For definiteness, in light of the yield criteria, we denote by F (TRR) the hardening function such that F = 0 is the chosen yield criterion ([7], ch. 76). We then define
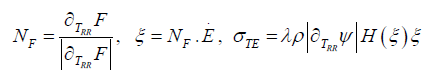
where H is the Heaviside step function and λ a non-negative parameter, possibly dependent on temperature. Accordingly, σTE ≥ 0 as required by (7). Upon substitution we obtain
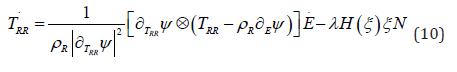
Some comments are in order about (10). The first term in the right-hand side can be viewed as the contribution of the elastic behaviour, the second one as the term providing hysteretic effects. If ψ is quadratic in TRR then N is collinear to TRR. This is consistent with flow rules where the plastic rate E˙p is in the direction of the stress. Sometimes the literature assumes the plastic strain rate in the form

where ζ is an appropriate measure of deformation. If, e.g., as in the von Mises criterion F is quadratic in the deviator of the stress then TRR ∂ F is proportional to TRR and we find again the flow rule in the direction of TRR. Furthermore, the yield criteria and the flow rules are usually stated in terms of the Cauchy stress T rather than of the Piola stress TRR; in linear approximations TRR T .
Acknowledgement
The research leading to this work has been developed under the auspices of INDAM-GNFM.
Conflict of Interest
No conflict of interest.
References
- Truesdell C (1984) Rational Thermodynamics, Springer, New York.
- Coleman BD, Noll W (1963) The thermodynamics of elastic materials with heat conduction and viscosity, Arch Rational Mech Anal 13: 167-178.
- Green AE, Naghdi PM (1977) On thermodynamics and the nature of the second law. Proc Roy Soc London A 357: 253-270.
- Rajagopal KR, Srinivasa AR (1999) On the thermodynamics of shape memory wires. Z angew Math Phys 50: 459-496.
- Giorgi C, Morro A (2020) A thermodynamic approach to hysteretic models in ferroelectrics, Math. Comp. Simul. 176: 181-194.
- Giorgi C, Morro A (2021) A thermodynamic approach to rate-type models in deformable ferroelectrics. Cont Mech Thermodyn 33: 727-747.
- Gurtin ME, Fried E, Anand L (2011) The Mechanics and Thermodynamics of Continua, Cambridge University Press, USA.
-
Claudio Giorgi, Angelo Morro. Thermodynamically Consistent Models of Elastic-Plastic Materials. Cur Trends Civil & Struct Eng. 7(5): 2021. CTCSE.MS.ID.000672.
-
Elastic-plastic materials, Thermodynamics, Energy density, Hysteretic effectst
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






