The Emerging Need for Civil Engineering Design to Embrace a New Systems Approach to the Solution of Complex Problems in Rapidly Changing Technical and Political Landscapes

Picture a scene of a wandering explorer hiking through a mountainous unexplored landscape. Without maps to show the way, how can they find the highest peak or indeed know if they are already on it? Through the mists clouding our view when travelling in the hills of new technology, it is often not clear if that next peak ahead is higher than the one which we are on. Maybe there are further peaks beyond which reach greater heights than any of those we can see from our current vantage point. Over relatively long periods of time, multiple expeditions can record ever better details of the terrain being navigated and eventually we develop a topographical map of the region so that those who follow us may climb to the pinnacle of achievement with the information we gather. This has been the traditional approach to engineering solution optimization since the industrial revolution when mechanical engineer, Frederick Taylor began developing principles of industrial efficiency. But what if the landscape becomes a seascape? In a terrain where we know there is a pinnacle of achievement to be scaled, if only we could find it and navigate to it; what if suddenly, we are faced with waves of peaks and troughs which rapidly change while we are on them. What if we are now chasing an optimal solution to a problem, only to find that, as we arrive at its location, we see that the highest crest has moved and is now where we have just travelled from?

In a modern world of complex problems, we appear to be faced with such a seascape. As engineers, we need to revisit the traditional methods of surveying our route. Navigating a fixed landscape now needs to facilitate adaptation to the changing crests and troughs of the new seascape on which we float. Frederick Taylor (the mechanical engineer who lends his name to Taylorism) once famously found the optimal size of the labourer’s shovel. In a steel foundry it was observed that given a choice of shovel size, labourers could optimise their daily output by selecting a shovel most appropriate to a particular job. The optimal size of the shovel varied depending on the material being moved. For hauling relatively light materials such as ash, larger shovels allowed much bigger quantities to be shifted more quickly. For coal and iron ore, increasingly smaller shovels were found to give increasingly productive outputs–up to a point where the shovels became too small to be useful for any material. The larger shovels, ideal for ashes were just too heavy when filled with coal and the coal shovels too heavy loaded up with iron-ore. On the other hand, the smallest shovel, ideal for use with iron-ore, was hardly big enough to move a worthwhile quantity of coal, let alone ash, in one swing. The experiment deduced that there was an optimal weight of shovel for an individual labourer, and this led to the design of a shovel alighting on a standard 21 lb payload for the average labourer to facilitate work at optimal performance. Problems such as this one considers the variable, shovel weight in this case, and plot a graph of productivity against that variable. Output of material rises with increasing shovel weight until the load begins to become too heavy to swing repeatedly all day and the efficiency curve descends down the opposite side of the peaked curve. Theories addressing questions of optimal engineering design and a systems approach to answering them have often used an analogy comparing the relative benefits of various possible solutions to landscapes of mountains and valleys. To illustrate the different types of problems faced by civil engineers, comparisons to different types of landscape have traditionally been invoked. To reach an optimal solution to an engineering problem, the explorer (in our case the design engineer) finds their way around the landscape until they reach the summit which represents the best solution to the question being posed. Problems may allow for multiple peaks in the landscape where a multi-variant analysis is necessary to determine which of the mountains in a range reaches the highest altitude or in other words, gives the optimal solution to the problem. Where the solution is to be found among a vast multitude of such peaks, the ability to arrive at the optimal solution is often a case of luck, intuition, experience or more recently, relatively complicated mathematical and statistical modelling. In traversing these landscapes there usually is a solution that remains optimal for enough time to be able to capitalize on it and exploit its benefits. Civil engineering designs from 200 years ago are often still relevant and functional in today’s world. Our landscape traditionally changes slowly.

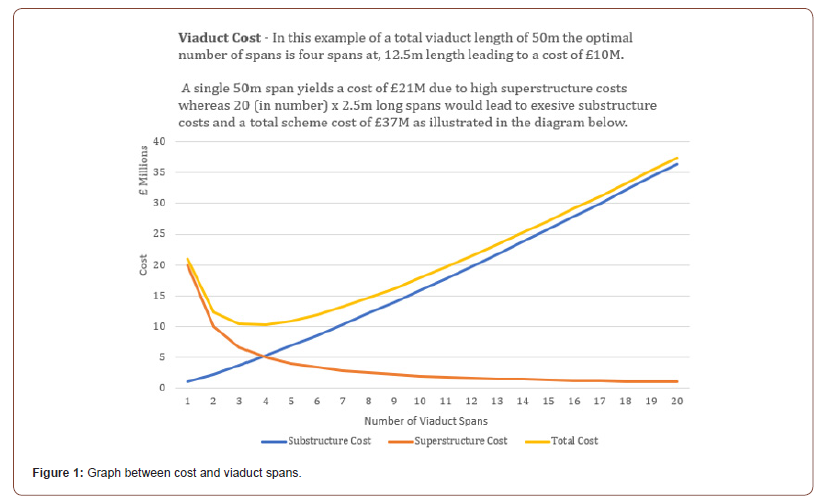
Engineers in the late 19th century and early 20th century developed techniques for solving problems which were based on simple deterministic mathematical models. The algorithms used to solve these models would assess the slopes in the landscape to find local peaks and establish the highest peak in the mathematical line or surface (be it three dimensional or multi-dimensional) mapping a function defining the solution to a particular problem. Such problems were relatively simple in nature and often had only one relevant solution to consider within a system governing the design of a particular civil engineering project. For example, in designing a multiple span viaduct bridge an engineer might have to consider the number of spans or, to consider its inverse, the choice of the distance between substructure piers defining the regular span lengths. The solution could be arrived at iteratively by selecting a span length and calculating the cost off the elements of the structure for multiple choices of span to a best guess of the optimal choice. Developing our techniques, a little further, in a simple mathematical analysis we might consider two variables within a cost model. Firstly, the cost of superstructure (the bridge deck) and secondly, the cost of the substructure (the piers and their foundations). As the number of spans decreases and the spanned distance between supports increases, the cost of the superstructure increases. This increase is typically based on some exponential function since the load effects – let us say, the beams’ internal bending moments for example – increase by some power term. Long span superstructure elements become very expensive to construct. Doubling the individual length of the spans taken to cross the gap, for example crossing a valley in two spans with a central pier instead of four spans, (each of a new length half that of the length of the two-span option) might lead to an increase in overall superstructure cost by a factor of four (a length squared term). When we now consider the substructure cost element in our model, the longer the spans are, the fewer of them are needed to cover the whole length of the structure. Directly related to this (proportional to it) is the number of substructure elements required and fewer of these substructure elements are required. The cost of the piers is clearly related to the number required so, conversely to the span costs; the cost of the substructure reduces as the spans increase in length. The total cost of the bridge viaduct therefore, in this, our simple model, is the sum of the cost of the superstructure and that of the substructure. At some selection of increasing span length, the overall cost of the scheme will arrive at some optimal solution. Since the cost curve is the inversely proportional to the optimization of the problem, we turn the cost curve upside down to arrive at out optimization “landscape” giving our “peak” solution (Figure 1).

For any given situation there is an optimal solution where the cost of the superstructure added to the cost of the substructure is at some minimum value. This optimal solution is largely dependent upon the ground conditions over which the viaduct must carry the road or railway. If the crossing conditions are particularly difficult, for example if there is a deep fast flowing river to cross, or the depth to solid rock foundations requires expensive deep piled foundations, the larger spans will reduce the significant cost of this element of the bridge up until the point where the cost of the spans begins to dominate the overall cost off the scheme. Conversely if the ground conditions lend themselves to multiple, relatively cheap sub structure components, the span superstructure costs will be predominant in the equation for the overall cost of the scheme and multiple smaller spans become the optimal solution in this instance. There are of course other factors at play in the real world and choices such as the type of bridge–cable stayed versus suspension or steel versus concrete produce an analogous mountain range of options. The techniques for optimizing solutions based on such variables are well established. That is to say, the figurative landscape on which operate is fixed with one optimum, highest mountain peak among the possible solutions or a handful of peaks in our mountain range which are close enough in height to be considered as legitimate alternative options to the solution of our bridge scheme design. Over time, the peaks in our analogous landscape may become slightly lower or higher as developments in material science and construction techniques chip away, weathering the landscape or raise new mountains like volcanoes rising above the others over comparatively geological timescales. The multispan brick arch viaducts of the Victorian era, once the most efficient method and ubiquitous in the viaduct world, give way to longer spans in wrought iron, steel or concrete, utilizing new construction innovations such as reinforced and prestressed concrete to create the modern architecturally beautiful and structurally wonderous cable stayed viaducts such as that by Michel Virogeux and Norman Foster at Millau. The immediate future may bring us composites with polymer components and carbon fibre reinforcement and new maps produced will help us navigate the slight shift in the peaks of the civil engineering world. Or will they?

Up to now, these techniques have developed slowly enough for the explorers and surveyors to keep pace with the analogously glacially slow landscape changes in a world where we design bridges to have a useful design life of 120 years or so. These changes in the design landscape have been slow enough to allow for the engineer’s “maps” – the codes of practice and specifications – to be updated regularly enough to keep pace. As we move towards a rate of change of technological best practice that is more analogous to a rapidly changing seascape, we will need a whole new set of maps and mapping strategies. Topographical models that change very rapidly. Too rapidly to keep pace with using our current mapping methods.

If, by the time it takes to secure public funding for a large transportation project, the peak of the wave we were once riding when we set out has suddenly dumps us into a white-water trough in our rapidly changing seascape, we risk pursuing solutions no longer relevant to the situation. This approach might be just as futile as deciding to build a brick arched railway viaduct reliant on Victorian methods of construction. The expedition we planned based on the maps we had at project inception may no longer relevant to the journey as we set out on the climb. The peak may move before we get to it. Techniques for complex systems analogous to these seascapes are being honed in industries such as telecommunications and the expansion of the internet which adapt in a lean and agile fashion. We, in our industry, should be finding new ways to apply the principles for navigating best solutions to the ever more quickly moving, “dancing” landscapes of the waves of change in civil engineering for a modern society.

None.

No conflict of interest.