Stochastic Modeling of Uncertainties in the Wind Load Pressure on Residential Buildings Using Different Stochastic Techniques

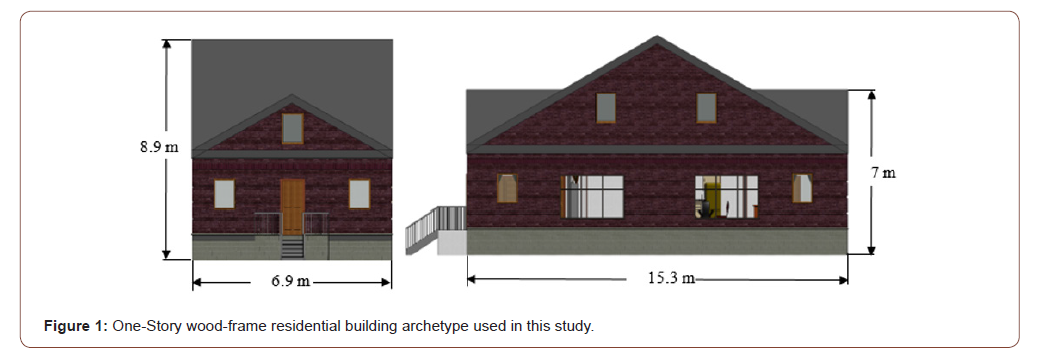
Wind hazard losses are catastrophic and devastating specifically for wind-driven by hurricane and tornados. The current literature is populated with many studies that investigate the impact of wind loads on buildings and infrastructure [1–4]. However, these studies, while they are novel, there is still a huge amount of uncertainties within the input parameters for the wind load calculation and the resistance of the impacted structures [5]. The current research trend in the vulnerability analysis of buildings and infrastructure to natural hazards is moving from deterministic to probabilistic approaches. This includes buildings vulnerability to earthquake hazard [6,7], wind hazards [8–10], and flood hazards [11,12]. However, the focus of this article is spotted on wind hazards and the quantification of the uncertainties associated with its parameters. Several probabilistic analyses of the wind load im-pacts on building and infrastructure were investigated in the literature including wind hazard induced by tornados [13–15] and hurricanes [16–19]. Additionally, multiple numerical and experimental studies in the literature focus on propagating uncertainties in wind damage models using fragility functions to describe the probabilistic performance of buildings and infra-structure [9,13,20–23]. Most all of these functions are using Monte Carlo simulation (MCS) to propagate uncertainties in the wind demand and capacity parameters based on a specific number of simulations. However, there are multiple approaches that could be used to propagate uncertainties ranging from simple to computationally expensive approaches. Additionally, the number of used simulations highly impacts the accuracy of the analysis results. Therefore, different stochastic simulation methods are needed to investigate the uncertainty quantification within wind load parameters including resistance and demand parameters. There are wide different stochastic simulation techniques that could be used to propagate these uncertainties. However, the suitability and the efficiency of each technique should be tested and compared to the other available methods. Therefore, in this paper, the uncertainties in the wind pressure model parameter will be propagated along with the uncertainties within the wind resistance parameters using different stochastic simulation techniques such as Direct Monte Carlo Simulation (MCS), Importance Sampling (IS), First Order Reliability Method (FORM), and Taylor Approximation (TA). This was done using an illustrative example building archetype to illustrate the proposed approach. Therefore, a one-story single-family woodframe residential building archetype is analyzed using a number of stochastic modeling techniques. The expected value of the resulted wind pressure on this archetype was investigated using different stochastic simulation techniques along with the failure probability of the building com-ponents (Figure 1).

There are wide different stochastic simulation techniques that could be used to quantify the amount of uncertainties within engineering systems. However, the main challenge is choosing the most suitable and efficient technique that fit each specific system and the characteristics of its parameters with the lowest number of simulations. Therefore, different stochastic models should be tested, and their analysis results should be compared to determine the most accurate and suitable techniques. In terms of wind load, when buildings are designed for wind, the wind pressure is the main characteristic load that buildings’ components get designed for. The most challenging aspect of the wind pressure quantification is the diversity of parameters included within the pressure equation that accounts for different types of buildings and wind load characteristics. Based on the ASCE7-16 [24], the extreme wind loads are calculated using Eqs. (1) and (2). The wind load analysis conducted herein does not include the tornado factors that have been included in multiple researches related wind hazards induced by tornados [13,25] as shown in Eq. (3). Therefore, the tornado factors are assumed to be 1.0 to make the analysis more general and simple.

where q_h = the wind velocity pressure calculated at mean roof height h; K_h= velocity pressure exposure coefficient atmean roof height; K_zt = topographic factor which is assumed to be deterministic and equal to 1.0 in this study; Kd = directionality factor which is also assumed to be deterministic and equal to 0.85; V = 3-s gust wind speed; G = gust-effectfactor;GCp= external pressure coefficient; GCpi= internal pressure coefficient. In the model presented herein, the uncertainty within K_h,G_Cp, and G_Cpi were propagated using the statistical models provided in these references[8, 10, 24] as shown in (Table 1).

Wind loads mainly impact the building envelop including walls sheathing and framing, roof sheathing and framing, doors, and windows. The behavior of these components controls the damage state (DS) of buildings subjected to wind loads as described herein [9, 13, 22, 23]. However, the most vulnerable building component is the exterior components. Therefore, the focus of this study is spotted on the roof sheathing, plywood covering, doors, and windows. A wood-frame residential building archetype developed by Amini and van de Lindt [8] is used herein as an example to illustrate the analysis approach. Table 2 lists the statistical models for some of these components which are provided by Unnikrishnan and Barbato [26] and Lee and Rosowsky [20]. Afterwards, different stochastic methods were used to account for the different uncertainties within the wind load parameters such as MCS, IS, FORM, and TA.

Table 1:Wind load statistics.

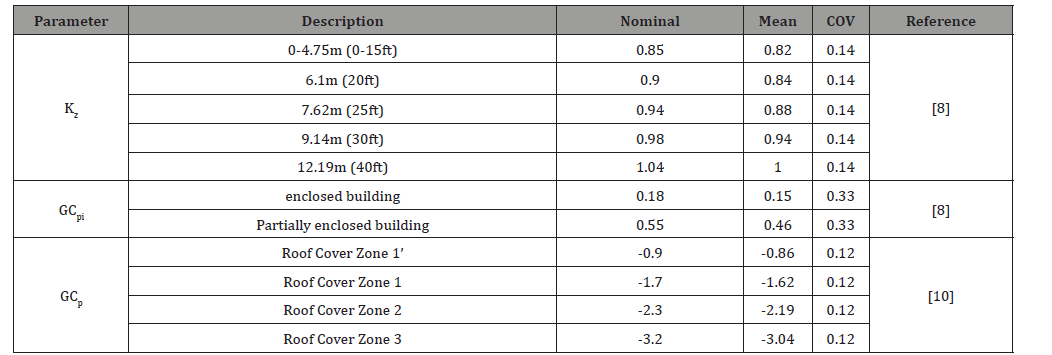
Table 2:Components resistance statistics.

The archetype selected herein is this study is one of the most common one-story residential building adopted in the US buildings industry. It is a one-story single-family wood residential building with a small rectangular plan of (15.3m × 6.9m) with a total area of 105 m2 (1130 ft2). The readers are referred to these articles [8, 22] for more details about the statistical parameters for the resistance of this archetype. Fig. 1 shows detailed dimensions of the chosen archetype. Additionally, the wind load parameters statistics are presented in Table 1 and the building components resistance statistics are presented in (Table 2).

First, the wind load pressure parameters statistics and the component’s resistance statistics were collected from the literature as discussed above. The mean value and the coefficient of variation of the wind pressure were calculated using MCS, IS, FORM, and TA with the goal of investigating the impact of the different stochastic modeling techniques on the resulted variation in the value of the wind pressure. The mean value was calculated by evaluating the general stochastic integral in Eq. 4 Then, the failure probability of the roof sheathing was calculated and compared the results from adopted methods.

where f(ξ) = the probability density function of the estimated parameter, g(ξ) = the scalar function of the random variable, and Ef[g(ξ)] of the random variable.

The Direct Monte Carlo simulation (MCS) technique depends on the Central Limit Theorem which includes developing a number of simulations for each random variable to quantify the estimator for Eq. (3). MCS is used to calculate the average value of the integral (Hk) by dividing the total number of the simulated values of the scalar function of the random variable (ξ) by the total number of simulations using Eq. (5). The MCS process conducted herein included generating 1000 samples in a standard Gaussian space to evaluate the wind pressure at each sample point. Then, the mean value and the coefficient of variation for the wind pressure was calculated. The coefficient of variation is calculated using Eq.(6).

The Importance Sampling (IS) technique is used to generate samples that are within the important region which will help to reduce the variance induced by MCS. Therefore, usually, the COV associated with IS estimator is lower than the one calculated using MCS. Using IS will help to find an optimal distribution that matches the original one by assuming a distribution close enough to the peak of the integrand. The optimal sampling density is assumed to have a positive relationship with the integrand in Eq.(4) whichis calculated using Eq.(7).

Taylor Approximation estimates the stochastic integral in Eq. (4) using Taylor series. The main goal of using Taylor series is to make the stochastic integral easier and suitable for the differentiation process by including exponential in the integrand as shown in Eq.(8). Then, the estimator for Eq. (4) was evaluated in Eq. (9) by using the second-order Taylor Polynomial and optimizing the integrand to calculate the Hessian Hlnk(ξ)

where k(ξ*) = is the value of the integrand function at ξ*, and Hlnk(ξ*) is the Hessian of the logarithmic value of the integrand evaluated at ξ*.

The First Order Reliability Method (FORM) depends on the simplification of the integrand using the idea that the probability density function gets decreased as we move away from the center of the distribution. In this method, a failure region F is assumed to be bounded by a certain threshold and there are some points ξ located within this threshold and other points ξ* with highest probability density function value. Hence, the points around ξ* will exhibit more contribution to the failure probability. The failure probability is the approximation of the F calculated from Eq.(10) which is a function of the reliability index 𝛽 calculated from Eq.(11). {

In the last part, different stochastic modeling methods were investigated to calculate the mean value of the wind pressure at the roof of the impacted residential buildings. The roof failure analysis is conducted by assuming the wind velocity to be 70.0 m/s which represents a category 4 hurricane on the Saffir-Simpson hurricane wind scale or category 3 tornado on the enhanced Fujita scale. Then, the calculated wind pressure will be compared with the resistance of the roof sheathing to calculate the failure probability of this component. The failure probability was calculated using failure indicator function F (ξ). The indicator function is equal to 1.0 in case of failure at wind pressure exceeding the resistance pressure value and is equal to 0.0 in case of no failure at wind pressure less than resistance pressure value. The failure probability will be calculated using Eq. (12).

The methods used to evaluate the mean value of the wind pressure were used to calculate the failure probability by replacing g(ξ) with IF (ξ). In addition to these methods, the first-order reliability method was also used to calculate the failure probability.

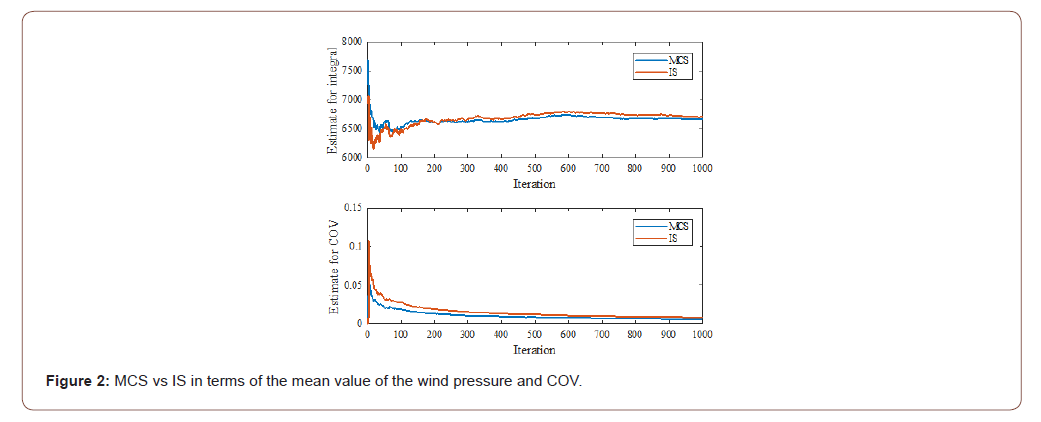
An algorithm that formulates these stochastic models was created using the static models of both wind demand parameters and the roof sheathing statistics. The number of simulations used to conduct the analyses related to each stochastic model is 1000 simulation. The mean value and COV of the wind pressure were calculated using MCS, IS, and Taylor Approximation . (Table 3) Summarizes the wind pressure results calculated from the different stochastic methods. The analysis results show that all the used methods gave very close results. However, MCS gave less coefficient of variation.

Table 3:The resulted mean wind pressure value and C.O.V using MCS, IS, and Taylor Approximation for the roof sheathing.

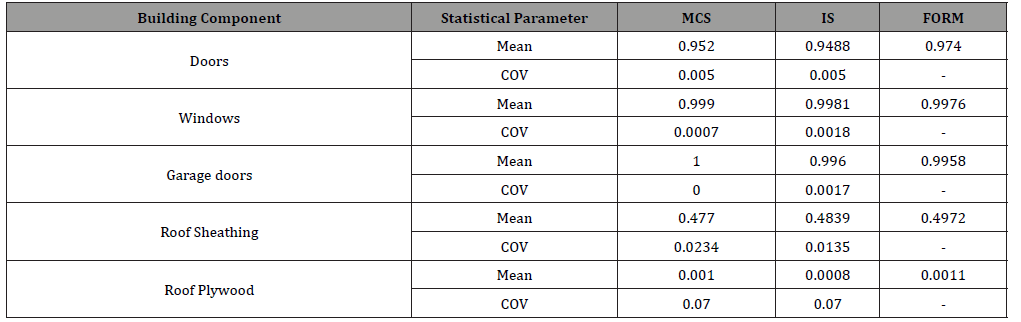
Figure 2 shows how the increase in the number of samples will result in stabilizing the value of the mean wind pressure. Increasing the number of samples is also increasing the efficiency of both MCS and IS method in reducing the coefficient of variation with the adopted number of samples. To that end, MCS is considered the most efficient with less COV. The failure probability for the different components of the selected residential building archetype was then tested using the same methods that have been used before in addition to the FORM method (Table 4). Presents the summary of the results from the different stochastic methods for the select building components. The results showed that the MCS is as efficient as the IS approach which gives almost the same variation resulted from the IS.

Table 4:The failure probability of the different building components along with the C.O.V using MCS, IS, and FORM.

The overarching goal of this study is to propagate uncertainties within the wind load pressure parameters using different stochastic simulation techniques to capture the impact of using different techniques on the wind pressure mean value and its variation. Therefore, Direct Monte Carlo Simulation, Importance Sampling, and Taylor Approximation were used to pick the efficient technique that will induce less coefficient of variation. Additionally, the failure probability of the building components was further investigated using Direct Monte Carlo Simulation, Importance Sampling, and First Order Reliability Method. The results showed that both Direct Monte Carlo Simulation and Importance Sampling method result in almost the same results in terms of the coefficient of variance of the wind load pressure. However, the MCS method gives less variation with less effort based on the low COV. In terms of failure probability of the different building components, the MCS method showed better efficiency than the other methods based on the resulted low coefficient of variance. So, Monte Carlo simulation did an outstanding performance in the wind pressure calculation with respect to the other methods. That is why all the wind load-based fragility analysis literature is based on the MCS analysis.

None.

No conflict of interest.

1. Pita G, Pinelli JP, Cocke S, Gurley K, Mitrani-Reiser J, et al. (2012) Assessment of hurricane-induced internal damage to low-rise buildings in the Florida Public Hurricane Loss Model. Journal of wind engineering and industrial aerodynamics 104: 76–87.
2. Aghababaei M, Koliou M, Paal SG (2018) Performance assessment of building infrastructure impacted by the 2017 Hurricane Harvey in the Port Aransas region. Journal of Performance of Constructed Facilities 32(5): 4018069.
3. Reinoso E, Niño M, Berny E, Inzunza I (2020) Wind Risk Assessment of Electric Power Lines due to Hurricane Hazard. Natural Hazards Review 21(2): 4020010.
4. Huang Z, Fan X, Cai L, Shi SQ (2016) Tornado hazard for structural engineering. Natural Hazards 83(3): 1821–1842.
5. Li Y, Ellingwood BR (2006) Hurricane damage to residential construction in the US: Importance of uncertainty modeling in risk assessment. Engineering structures 28(7): 1009–1018.
6. Aghababaei M, Mahsuli M (2018) Detailed seismic risk analysis of buildings using structural reliability methods. Probabilistic Engineering Mechanics 53: 23–38.
7. Aghababaei M, Mahsuli M (2019) Component damage models for detailed seismic risk analysis using structural reliability methods. Structural Safety 76: 108–122.
8. Amini MO, van de Lindt JW (2013) Quantitative insight into rational tornado design wind speeds for residential wood-frame structures using fragility approach. Journal of Structural Engineering 140(7): 4014033.
9. Memari M, Attary N, Masoomi H, Mahmoud H, van de Lindt JW, et al. (2018) Minimal building fragility portfolio for damage assessment of communities subjected to tornadoes. Journal of Structural Engineering 144(7): 4018072.
10. Ellingwood BR, Tekie PB (1999) Wind load statistics for probability-based structural design. Journal of Structural Engineering 125(4): 453–463.
11. Nofal OM, van de Lindt JW, Do TQ (2020) Multi-variate and Single-variable Flood Fragility and Loss Approaches for Wood Frame Buildings. Reliability Engineering & System Safety 106971.
12. Nofal OM, van de Lindt JW (2020) Minimal Building Flood Fragility and Loss Function Portfolio for Resilience Analysis at the Community-Level. Water 12(8): 2277.
13. Masoomi H, van de Lindt JW (2016) Tornado fragility and risk assessment of an archetype masonry school building. Engineering Structures 128: 26–43.
14. Unnikrishnan VU, van de Lindt JW (2016) Probabilistic framework for performance assessment of electrical power networks to tornadoes. Sustainable and Resilient Infrastructure 1(3–4): 137–152.
15. Standohar-Alfano CD, van de Lindt JW (2016) Tornado risk analysis for residential wood-frame roof damage across the United States. Journal of Structural Engineering 142(1): 4015099.
16. Kakareko G, Jung S, Mishra S, Vanli OA (2020) Bayesian capacity model for hurricane vulnerability estimation. Structure and Infrastructure Engineering 1–11.
17. Mishra S, Vanli OA, Alduse BP, Jung S (2017) Hurricane loss estimation in wood-frame buildings using Bayesian model updating: Assessing uncertainty in fragility and reliability analyses. Engineering Structures 135: 81–94.
18. Khajwal AB, Noshadravan A (2020) Probabilistic Hurricane Wind-Induced Loss Model for Risk Assessment on a Regional Scale. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering 6(2): 4020020.
19. Ouyang M, Duenas-Osorio L (2014) Multi-dimensional hurricane resilience assessment of electric power systems. Structural Safety 48: 15–24.
20. Lee KH, Rosowsky DV (2005) Fragility assessment for roof sheathing failure in high wind regions. Engineering Structures 27(6): 857–868.
21. Van de Lindt J, Amini MO, Standohar-Alfano C, Dao T (2012) Systematic study of the failure of a light-frame wood roof in a tornado. Buildings 2(4): 519–533.
22. Masoomi H, Ameri MR, van de Lindt JW (2018) Wind performance enhancement strategies for residential wood-frame buildings. Journal of Performance of Constructed Facilities 32(3): 4018024.
23. Koliou M, Masoomi H, van de Lindt JW (2017) Performance assessment of tilt-up big-box buildings subjected to extreme hazards: Tornadoes and earthquakes. Journal of Performance of Constructed Facilities 31(5): 4017060.
24. ASCE (2016) Minimum Design Loads and Associated Criteria for Buildings and other Structures (7-16).
25. van de Lindt JW, Pei S, Dao T, Graettinger A, Prevatt DO, et al. (2013) Dual-objective-based tornado design philosophy. Journal of Structural Engineering 139(2): 251–263.
26. Unnikrishnan VU, Barbato M (2016) Performance-based comparison of different storm mitigation techniques for residential buildings. Journal of Structural Engineering 142(6): 4016011.