 Review Article
Review Article
Simultaneous Determination of Technical, Social, Environment and Economic Feasibility in a Portfolio of Construction Projects, followed by the Selection of Best Projects, Using the SIMUS Method
Nolberto Munier, Valencia Polytechnic University, Spain.
Received Date: September 09, 2020; Published Date: September 29, 2020
Abstract
This paper introduces a subject that is not often seen in the Multi Criteria Decision-Making (MCDM) literature, or perhaps never seen, and it is related to determining if a complex undertaking is feasible, considering the multiples restrictions that commonly exist. This is a very common situation in civil construction where an entrepreneur has a portfolio of different constructions, for instance, building a set of dwellings with different types of structure, including complementary ancillary. There are resources that must be employed rationally such as funds, manpower, equipment, concrete, etc., which are used in all projects, and because the limitation of supplies and timing, they may render the whole scenario unfeasible. This paper addresses this issue by determining if the undertaking as a whole is feasible, considering all restrictions, and if it is, identifying the best projects and the scope of each one. A real example for pulp, paper and sawmill complex is proposed and solved using the SIMUS method of MCDM. This is followed by a sensitivity analysis of the solution.
Keywords: Feasibility; Restrictions or Criteria; SIMUS; Logging; Lumber; Pulp mill; Paper mill; Sawmill
Introduction
In Civil Engineering there are many scenarios that deal with the selection and construction of diverse options in a portfolio of projects, similar or dissimilar. That is, an entrepreneur may have a portfolio of say four construction projects of different magnitude, investment, profitability, and even of various kinds. All these projects, albeit different, are subject to a set of conditions regarding several aspects. Normally, feasibility of a unique project is computed regarding financial, economic and expected return on investment; the same applies, but it is far more complex, when there are many projects, all of them subject to a set of conditions that can be similar or different, as for instance, the use of available resources shared by some projects. In addition, the entrepreneur estimates the investment for each one of four different undertakings or options, however, he must consider that all of them are related - other than by limited available funding–on other aspects such as cost, environmental limits, execution time, different construction rate, risk, annual budget, etc. That is, the entrepreneur must be sure that whatever the selection made, there must be enough resources, sufficient funds, adequate manpower, availability of construction equipment, etc., and in addition, used as efficiently as possible. He needs to consider that if a backhoe is needed for the four projects, its use has to be combined in such a way that the equipment is not idle, nor a work stopped because it is not available. This is common problem in construction works. However, we must also be concerned that all the other conditions are analyzed in the same way, that is concrete, manpower, water, energy, etc., all of which are limited, and available in time and in quantity. It is then necessary to be sure that with the resources the company has, and considering the four undertakings, if the complete undertaking is feasible, that is, that they can be executed simultaneously or in stages, but achievable. This is the meaning of project feasibility. It aims at pointing out then necessity of making sure that the whole scenario is viable, and that a variation of any of the different conditions does not affect the result. As a simple example: Assume that a farmer cultivates crops as barley, wheat and maize in a 20 has plot. He has computed the minimum amount of each crop he needs to produce, to recover the capital invested and make a profit. Of course, he must consider different inputs related with seeds, fertilizers, manpower, water, etc. Assume that water is received through a municipal distribution metered system, and say he is entitled to 150,000 m3/ yr. However, he did not realize that said amount of water is short to cover all his water needs, and taking into account that each crop has different water demands, consequently, the undertaking as planned is not feasible. That should have been detected before attempting any selection. To make it feasible, maybe he has to reduce the barley in say 4 has., however, it could be that said reduction involves that the money he can get from the sale of barley, is not enough to compensate costs. Again, the undertaking is not feasible. What is analyzed for water must be also analyzed for all other inputs. As can be understood, determining feasibility is important in a single problem, and very complicated when we are dealing with several projects. This scenario can be solved using Multi Criteria Decision- Making (MCDM).
Objective of this paper: The objective of this paper is to select the best alternative or option, but more important, it aims at finding if the proposed scenario is feasible in its integrity, that is, if it is realistic considering the alternatives and the restrictions imposed to them as well as conditions that must satisfy. The paper has a first part as introduction, and a second with information about the SIMUS [1] method. The third step proposes the case and solves it. The fourth step is dedicated to the sensitivity analysis of the solution found, in order to find how strong or stable is the alternative selected when some options vary. The result does not pretend to be the perfect solution, but a guide and support for the DM and stakeholders, which can take decisions based on a mathematical result.
The SIMUS method
The SIMUS (Sequential Interactive Model for Urban Systems) [1], a MCDM method, is based on Linear Programming (LP) [2], with its algorithm (The Simplex), created by Dantzig [3], and an add-in in the Excel spreadsheet since 1993, under the name of Solver [4,5] to resolve the Simplex. The method falls in the Multi Criteria Decision- Making (MCDM) area, a very well-known and used discipline, and applied world-wide in thousands of projects, in many different fields. SIMUS uses Solver to find, if it exists, the best solution. If it can’t find it, it announces that there is not a feasible solution, and then, the whole problem has to be revamped. If as usually happens, each criterion is satisfied, then we can be sure that the scenario is feasible, and that the obtained result is credible. Please consider that in SIMUS, criteria Ci and objectives Zi have the same structure, however, with different values and purposes; Zi are the output of inputted criteria Ci, Criteria are used to evaluate alternatives, and objectives inform about how well the best solution complies with criteria. It is evident that not all criteria have the same significance and this is widely recognized in practically all MCDM methods, by assigning weights to criteria, normally obtained by using personal preferences, from the Decision-Maker (DM) or stakeholders, and thus, subjective. In LP there are not such weights, albeit it does not ignore the difference importance of criteria. Relative criteria significance is computed internally, using data imputed; as a consequence, the result is totally objective, reached by a mathematic algorithm. However, this result is merely informative on ‘excellence’, and then it is for the DM and stakeholders to analyze, ponder and accept, modify or simply reject it. Fundamentally, if SIMUS finds a result it means that the whole project is feasible. SIMUS has also the ability to consider a variety of common issues such as precedent relationships among alternatives. Sensitivity analysis explores the sensitivity of the best solution, that is, the best option, considering potential simultaneous variations of several criteria. Again, SIMUS does not work with weights as the present-day systems, but with marginal utilities for criteria, which allows for drawing the total utility curve of each objective, related to the best solution.
A Case Related to the Wood Industry
The wood industry originates in forest logging and has three main avenues: Paper pulp manufacturing, Paper production and logs industrialization, that is, Lumber. Pulp is the raw material for making paper, and consists in chemically treating chips, produced by a sawmill, to remove the lignin and, hence freeing the fiber. Paper has a wide spectrum of applications in newspapers and magazines, commercial and industrial offices, packing, boards, boxes, and a myriad of applications from printing books to material for students. The sawmill produces debarked logs, chips and lumber that has heavy use in the construction of houses structure in form of studs, joists, rafters (sloping timbers), etc., especially in countries with cold weather as in North Europe, United States and Canada, and south-west Argentina, as well as raw material for carpentry, panels, bridges, furniture, panels, etc. MCDM is used for selecting the best options or alternatives among others. It starts by building a decision matrix formed by alternatives, in this case the sawmill, pulp mill and papermill, which are subject to a series of conditions called criteria. These criteria must be confirmed by the selected project. The project that satisfies the largest number of criteria is option may be very good in satisfying certain criteria, but behaving very poorly with others. It is obvious that there is not an option that is the best in all criteria; if this could happen, no computation would be necessary, since naturally, it would be the best. In addition, there are normally cases where the alternatives have values for a certain criterion that are very close among them. In this case, it is obvious that said criterion is not good for selection, since there are no large differences between the options. There are different kinds of criteria, some have realistic values such as the cost of a certain equipment; they are quantitative criteria. Others have qualitative data which is generally uncertain and can come from surveys, statistics or by the Decision-Maker (DM) knowledge. Normally, the construction of this type of undertaking is controversial among the people living in the area. The reason is that it can benefit them because it is a job generator, and thus, with the capacity to improve the living conditions of many people. Consequently, normally there is a wide acceptance of the undertaking. However, often, and especially in this type of projects there are aspects that people don’t like, for instance, odors, air contamination, water contamination, forest erosion that can produce landslides, etc., therefore, people may have a negative comment about each of the different projects. There would be many additional criteria, may be in the hundreds, addressing in more detail financial issues, as well as on environment, type of equipment to be purchased, efficiencies, environmental tolerances, legal aspects, people claim, etc. Consequently, this work could be taken as a sort of a pre-feasibility study considering the options subject to the most essential and significant criteria. The mathematical result is then a guide, an objective base for the stakeholders, about what is apparently the most promising alternative, and to determine if the whole scenario is feasible.
The case
This case refers to an international company with forest rights around the world, which wants to build a new industrial complex in Canada, based on logging. For the supply of logs (that is, fallen trees), they can build the sawmill near their forests, or they can get the logs from other companies. In addition, there is a restriction of precedence, since if say the paper mill is selected it must be preceded by the pulp coming from their own mill. For the same token, the construction of the sawmill must precede that of the pulp, since this is fed with chips from the sawmill. This study aims at determining which is the best project to undertake, that is, a pulp mill, a paper mill or a sawmill. However, the construction of the sawmill and even the construction of the pulp mill can be independent to the paper mill, since the cellulose paste may be sold to a third part. Of course, another solution is to build only the paper mill, and in this case the cellulose paste must be obtained from another company.
Therefore, the potential construction could be:
Build the sawmill (ID=3) alone
Build the sawmill (ID=3) and the pulp mill (ID=1)
Build the paper mill alone (ID=2)
Build the three plants, however, this option is not possible because capital restrictions.
This is a rather complicated problem, especially because the precedence. To solve it the author utilized the SIMUS method. There is a total of 13 criteria that correspond to the financial, technical, social and environmental areas, and all of them must be considered simultaneously.
The criteria (Ci) are:
C1: IRR or Internal Rate of Return, in %, estimated by the company Financial Department,
C2: NPV or Net Present Value, in Canadian Dollars (CAD) estimated by the company Financial Department,
C3: Debt coverage, in %, estimated by the company Financial Department,
C4: Risk, in %, computed following the Z method for chained risks (Munier et al 2019), computed by stakeholders,
C5: Construction cost, in millions of CAD, from the Engineering Department, includes Operating and Working Capital, as well as Land cost,
C6: Complexity, in Likert scale, estimated by experts,
C7: Equipment cost, from suppliers offers,
C8: People opposition, in %, from a survey, performed by company the Public Relations Department,
C9: Wild Life, estimated by environment specialists in the Likert scale,
C10: Particulates emissions, in tons, evaluated by equipment’s suppliers,
C11: CO2 contamination, in tons, value furnished by equipment’s suppliers and company experts,
C12: PFA (per-and polyfluoroalkyl substances), in mg/m3, evaluated from company experts, in pounds/day,
C13: Particulates spewed by the sawmill, in mg/m3, estimated by the company Environment Department, and suppliers, as
well as experts on filtering equipment.
The alternatives, as mentioned are:
1- Pulp mill working with the Kraft principle,
2- Paper mill,
3-Saw mill
The initial matrix is shown in Table 1 (Table 1).
Table:Initial Decision Table.
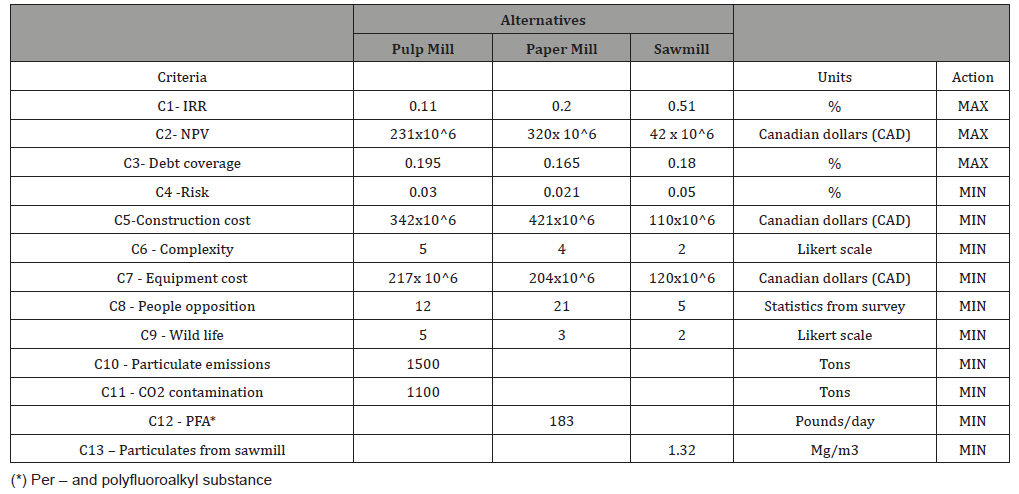
When Table 1 is transferred to SIMUS, we get Figure 1 (Figure 1).
Observe that from Table 1 have been added in Figure 1 the different actions for each criterion that is, maximize or minimize, with the corresponding mathematical symbol. Notice at upper right a little table that allows for inputting the precedents, that is that project 1, pulp mill must precede project 2 or paper mill, and that project 3, or sawmill must precede project 1. When solved, Figure 2 shows SIMUS final screen. Observe that precedents hold since Pulp mill with a score of 1.03 > Paper mill with a score of 0.17. Also, the Sawmill with a score of 10.06 > Pulp mill with a score of 1.03 (Figure 2).
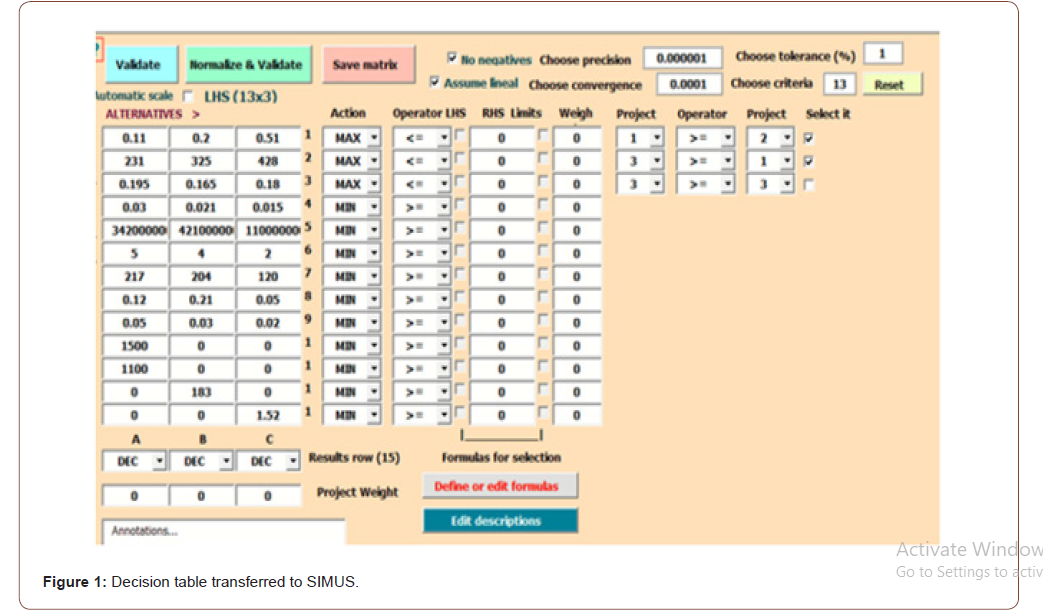
Scenario feasibility
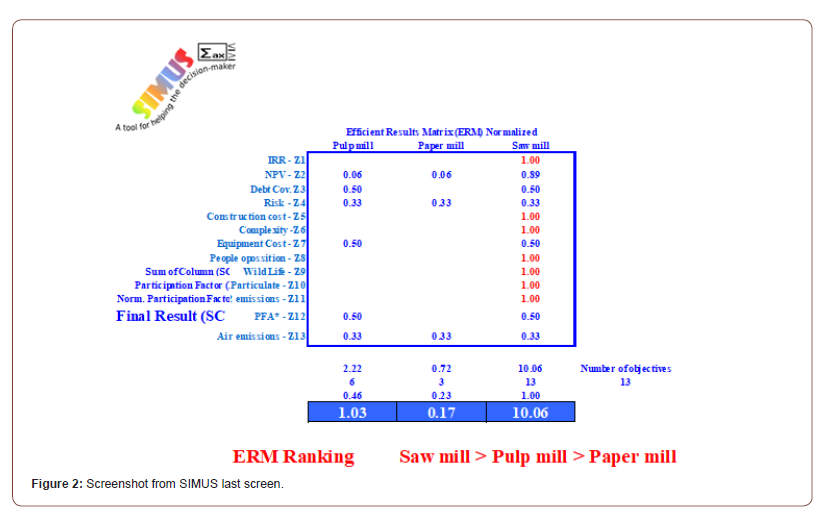
How do we know that the whole scenario is feasible, because this is only a mathematical calculation for selecting the best alternative? First of all, SIMUS will announce automatically if there is an unfeasible solution for a certain objective. See Figure 3, which is from another project, and proposed just as an example. It can be seen that SIMUS shows a shaded criterion 8 and in addition adds the sentence ‘Does not converge’, that is, for this objective there is not a feasible solution, therefore, the selection made does not comply with this restriction. Suppose for instance, that C8 criterion calls for minimizing NOx contamination, and was given a maximum allowable value or limit, established by environmental authorities. Then, it means that the whole project does not meet this requirement, and then can be rejected by those same authorities. This can be perhaps solved with a change in procedures, and then altering all other criteria such as cost, space, operating costs, etc. It can be appreciated with this simple example the significance of determining if a scenario is feasible (Figure 3).
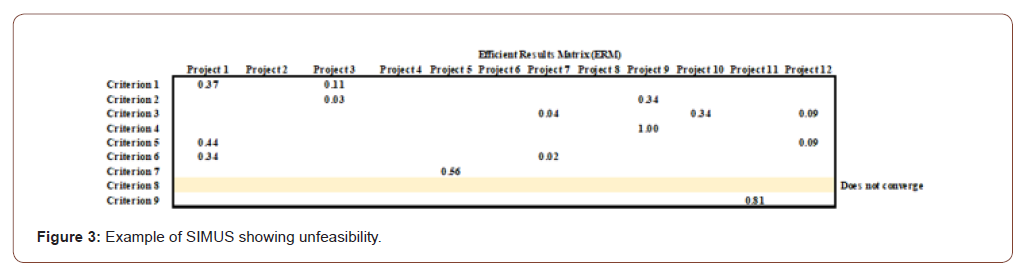
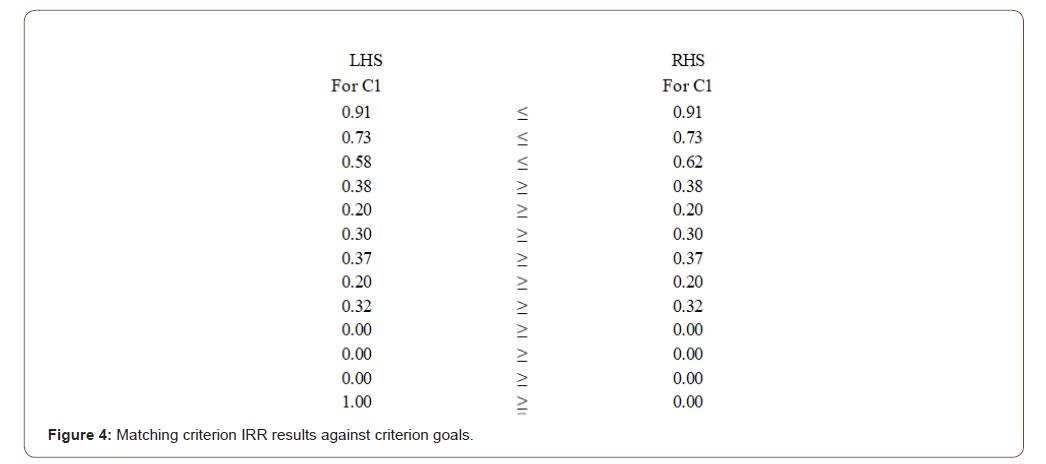
Second SIMUS last screen provides quantitative information about that. This is done by comparing if the stated goal or limit for a single criterion is satisfied. It can be easily done by comparing, for each criterion the value of the solution for than criterion, called LHS (It refers to the left hand side or member of the corresponding inequality) with reference with the previously goal for that criterion, which is called the Right Hand Side (It refers to the right hand side or member of the inequality). Both are linked by the ‘≤’ symbol, meaning ‘Less or equal than’ which is used for maximizing actions, or by the ‘≥’ symbol, meaning ‘Greater or equal than’ corresponding to minimizing actions. If, from comparing the LHS value with the RHS value for each criterion, this inequality is held, then there is feasibility. That is, if say LHS = 0.28 and RHS = 0.31, when the criterion calls for maximization, then the inequality holds. The RHS means the highest value that this criterion can reach, consequently, if LHS is lesser or equal that this value, there is viability. An example is if the criterion refers say to available funds; if the amount of funds from performing this criterion is less or equal that the maximum amount of money, everything is OK The ‘≥’ indicates the minimum amount that the criterion must consider. If for example the criterion refers to minimizing stock, but requires a minimum quantity to hold (RHS), the result of LHS must be equal or greater than this value. Thus, the criterion expresses than ‘You can use as much stock as you want, but always above a minimum, in order not to leave zero stock’. In the case that funds have to be exactly spent in a certain amount, then, the symbol’ =’ is used. Figure 4 reproduces this comparison for our problem when for instance, criterion 1 (IRR) is analyzed. Check that all values in the LSH column match the corresponding values in the RHS column, and then, meaning that from the IRR point of view, the selection is viable. This matching must be confirmed by the 13 criteria, and it is given by SIMUS (Figure 4).
Sensitivity Analysis
It is important to determine if the best solution found, that is to build the sawmill is strong or stable. This means finding if variations of criteria that are responsible for this election, alters the result or modify the ranking. This is called ‘Sensitivity Analysis’ (SA), since it examines the sensitivity of the solution to variation of some parameters. The last of SIMUS screens give complete information to perform this very important activity. From this analysis, it appears that the most important criterion is C6, that is, the variation of the complexity criterion, that naturally calls for minimizing. The intervening objectives (Zi) for this best selection are:
Z1: IRR, depending on C6 (complexity), with an allowed variation range of 0.09 on a value of 0.30, and meaning that increasing the complexity, decreases the IRR (because it has a negative marginal value). Consequently, we can increase the complexity from 0.30 to 0.39 without modifying the best solution.
Z5: Construction cost, depending on C6 (complexity), with an allowed range of 0.09 on a value of 0.30, meaning that increasing (because it has a positive marginal value) complexity from 0.30 to 0.39, increases the construction cost without modifying the solution.
Z8: People opposition, depending on C6 (complexity), with an allowed range of 0.09 on a value of 0.20, meaning that an increasing complexity from 0.30 to 0.29 increases people opposition, that is there is more resistance from people.
Z10: Particulates, depending C6 (complexity), with an allowed range of 0.09 on a value of 0.30, meaning that an increasing complexity from 0.30 to 0.39 increases the particulates emissions, which makes sense, because if the structure of the sawmill is for instance augmented by the addition of another operation, as the production of particle boards from sawdust, emissions will increase.
Z11: CO2 contamination, depending on C6 (complexity), with an allowed range of 0.09 on a value of 0.30, meaning that an increasing in complexity from 0.30 to 0.39, will increase CO2 contamination, for instance adding a kiln by turning green lumber into dry lumber.
The other criteria are irrelevant. It is notorious that in all cases, complexity plays a significant role in plant operation.
Conclusion
Feasibility of a project was explained, and an actual problem was proposed to show how feasibility of a project can be appraised using a method of MCDM, that at the same time makes the best possible selection. A thorough sensitivity analysis was performed and found that the solution achieved is strong and stable. It is believed that this is new procedure that can help the construction companies by giving reliable data and suggestions based on a rational analysis of each case.
Acknowledgment
None.
Conflict of Interest
No conflict of interest.
References
- Munier N (2011) A Tesis Doctoral - Procedimiento fundamentado en la Programación Lineal para la selección de alternativas en proyectos de naturaleza compleja y con objetivos múltiples- Universidad Politécnica de Valencia, Españ
- Kantorovich L (1939) The best uses of economic resources.
- Dantzig G (1948) Linear Programming and extensions. United States Air Force.
- Fylstra D (2018) (Solver) https://www.solver.com/Accessed: May 05, 2018.
- Munier N, Hontoria E, Jimenez F (2019) Strategic Approach in Multi-criteria Decision Making – A Practical Guide for Complex Scenarios – Springer. Switzerland.
-
Nolberto Munier. Simultaneous Determination of Technical, Social, Environment and Economic Feasibility in a Portfolio of Construction Projects, followed by the Selection of Best Projects, Using the SIMUS Method. Cur Trends Civil & Struct Eng. 6(3): 2020. CTCSE.MS.ID.000640.
-
Feasibility, Restrictions or Criteria, SIMUS, Logging, Lumber, Pulp mill, Paper mill, Sawmill, Magnitude, Investment, Profitability, Resources, Sufficient funds, Adequate, Manpower
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






