Review Study of Dynamic Relaxation Numerical Technique Used in Bending of Laminated Composite Plates

In the present work, finite differences coupled with dynamic relaxation (DRM) Method, which is a numerical technique, is used. The DRM method was first proposed and developed in 1960; see Rushton KR [1], Cassell AC & Hobbs RE [2], Day AS [3]. In this method, the equations of equilibrium are converted to dynamic equations by adding damping and inertia terms. These are then expressed in finite difference form and the solution is obtained by an iterative procedure as explained below.

The DRM formulae begin with the dynamic equation, which can be written as:

Where f is a function of the stress resultants and couples, u is referred to as a displacement, are the velocity and acceleration respectively, and k are the inertia and damping coefficients respectively, and t is time.

The formulation is completed by computing the stress resultants and stress couples from the known displacement field. The iterative procedure begins at time t=0 with all initial values of the velocities, displacements, and stresses equal to zero or any suitable values. In the first iteration, the velocities are obtained from equation (4), and the displacements from equation (5). After the satisfaction of the displacement boundary conditions, the stress resultants and stress couples are computed and the appropriate boundary conditions for stresses are applied. Subsequent iterations follow the same steps. The iterations continue until the desired accuracy is achieved.

Dimensional plate equations

The equations concerning the analysis of plates in bending (i.e. Equations (6), (7), (8), (9), and (10) are derived in Turvey & Osman [4-6] and Osama Khayal [7-9]. The first integrated equations of equilibrium can then be written in the following form:

Hence the integrated moment equilibrium equations are:

Non-dimensional plate equations

The plate equations can be written in non-dimensional form as follows:

Substituting equation (11) into equations (6), (7), (8), (9) and (10) then the non-dimensional dynamic plate equations are obtained. In the following equations, the primes are omitted:

The next step is to transform the differential equations into finite difference equations.

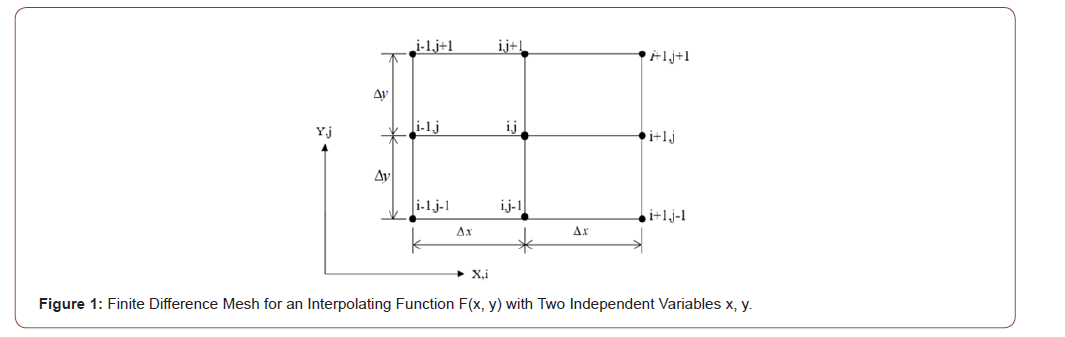
Interpolating function F (x, y)

It can be shown by using Taylor’s series that the first and second derivatives of a function F(x, y) at an arbitrary node i, j shown in figure 1 can be written as follows:

The velocity equations

According to equation (4) and from the equations of motion of the plate, i.e. equations (12), the velocities are determined as follows:-

In equations (16) __ (20), F1(i,j) , F2(i,j), F3(i,j), F4(i,j) and F5(i,j) are the finite difference approximations of the terms on the left hand side of the dynamic equations (12), i.e.

The displacement equations

The displacements are obtained using the velocities that are explained in Eqns. (16) to (20) as follows:

The stress resultants and couples equations

The finite difference approximations of the stress resultants and stress couples can be obtained using the following two equations (23) and (24) as stated below.

Hence, the finite difference approximations of the stress resultants and stress couples equations can be represented in the form:

Estimation of the fictitious variables

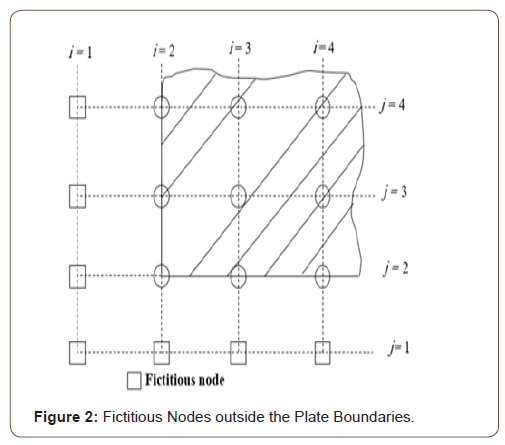
To compute the derivatives of displacements, stress resultants and stress couples at the boundaries of a plate, fictitious nodes are considered by extending the finite difference mesh beyond the boundaries as shown in Figure 2. The values of the variables at the fictitious nodes are known as fictitious values. The fictitious values are estimated in order to eliminate the third derivative of the interpolating function, which is quadratic.

Referring to Figure 2, the fictitious values at the points defined by (1, j) can be obtained by extrapolation as follows:

In the DRM technique, explained in the previous sections of this chapter, the static equations of the plate have been converted to dynamic equations i.e. equations (12). Then the inertia and damping terms are added to all of these equations. The iterations of the DRM technique can then be carried out in following procedures:

1. Set all initial values of variables to zero.

2. Compute the velocities from equations (16)-(20).

3. Compute the displacements from equations (22).

4. Apply suitable boundary conditions for the displacements.

5. Compute the stress resultants and stress couples from equations (25) to (32).

6. Apply the appropriate boundary conditions for the stress resultants and stress couples.

7. Check if the convergence criterion is satisfied, if it is not repeat the steps from 2 to 6.

It is obvious that this method requires five fictitious densities and a similar number of damping coefficients so as the solution will be converged correctly.

The computation of the fictitious densities based on the Gershgorin upper bound of the stiffness matrix of a plate is discussed in Cassel & Hobbs [2]. The fictitious densities vary from point to point over the plate as well as for each iteration, so as to improve the convergence of the numerical computations. The corresponding expressions for the computations of the fictitious densities are given below:

The following fictitious densities have been derived using the procedure proposed by Cassel & Hobbs [2]. With reference to Figure 2.

Where the over lined quantities are given by:

The DRM program is designed for the analysis of rectangular plates irrespective of material, geometry, edge conditions. The functions of the program are as follows: read the data file; compute the stiffness of the laminate, the fictitious densities, the velocities and displacements and the mid-plane deflections and stresses; check the stability of the numerical computations, the convergence of the solution, and the wrong convergence; compute through-thickness stresses in direction of plate axes; and transform through-thickness stresses in the lamina principal axes. The convergence of the DRM solution is checked, at the end of each iteration, by comparing the velocities over the plate domain with a predetermined value, which ranges between 10-9 for small deflection and 10-6 for large deflection. When all velocities are smaller than the predetermined value, the solution is deemed converged and consequently the iterative procedure is terminated. Sometimes DRM solution converges to invalid solution. To check for that the profile of variable is compared with the expected profile over the domain. For example when the value of the function on the boundaries is zero, and it is expected to increase from edge to center, then the solution should follow a similar profile. And when the computed profile is different from that expected, the solution is considered incorrect and can hardly be made to converge to the correct answer by altering the damping coefficients and time increment. Therefore, the boundary conditions should be examined and corrected if they are improper.

Time increment is a very important factor for speeding convergence and controlling numerical computations. When the increment is too small, the convergence becomes tediously slow; and when it is too large, the solution becomes unstable. The proper time increment in the present study it is taken as 0.8 for all boundary conditions. The optimum damping coefficient is that which produces critical motion. When the damping coefficients are large, the motion is over damped and the convergence becomes very slow. And when the coefficients are small, the motion is under damped and can cause numerical instability. Therefore, the damping coefficients must be selected carefully to eliminate under damping and over damping. The errors inherent in the DRM technique include the discretization error that is due to the replacement of a continuous function with a discrete function, and an additional error because the discrete equations are not solved exactly due to the variations of the velocities from the edge of the plate to the center. Finer meshes reduce the discretization error, but increase the round-off error due to the large number of calculations involved. The last type of error is relative to the rank of the interpolating function employed i.e. quadratic, cubic, etc. Refer to Osama Khayal [10-12].

None.

No conflict of interest.

1. Rushton KR (1968) Large Deflexion of Variable-thickness Plates. International Journal of Mech Sciences 10: 723-735.
2. Cassell AC, Hobbs RE (1966) Numerical Stability of Dynamic Relaxation Analysis of Nonlinear Structures . International Journal for Numerical Methods in Engineering 35(4): 1407-1410.
3. Day AS (1965) An Introduction to Dynamic Relaxation. the Engineer 219 (5688): 218-221.
4. Turvey GJ, Osman M.Y (1990) Elastic large deflection analysis of isotropic rectangular Mindlin plates. International Journal of mechanical sciences 22: (1-14).
5. Turvey GJ, Osman MY (1989) Large deflection analysis of orthotropic Mindlin plates. proceedings of the 12th Energy resource technology conference and exhibition, Houston, Texas, pp.163-172.
6. Turvey GJ, Osman MY (1991) Large deflection effects in anti-symmetric cross-ply laminated strips and plates. I.H. Marshall, composite structures, vol.6, Paisley College, Scotland, Elsevier Science publishers, pp. 397-413.
7. Osama Mohammed Elmardi (2014) Verification of dynamic relaxation method in isotropic, orthotropic and laminated plates using small deflection theory”, International Journal of Advanced Science and Technology 72: 37-48.
8. Osama Mohammed Elmardi (2015) Nonlinear analysis of rectangular laminated plates using large deflection theory”, International Journal of Engineering Technology and Research 2(5): 26-48.
9. Osama Mohammed Elmardi (2015) Validation of dynamic relaxation (DRM) method in rectangular laminates using large deflection theory”, International Journal of Advanced Research in Computer Science and Software Engineering 5(9): 137-144.
10. Osama Mohammed Elmardi Suleiman (2015) Nonlinear analysis of rectangular laminated plates. Lap Lambert Academic Publishing, Germany, and ISBN: 978-3-65976787-6.
11. Osama Mohammed Elmardi Suleiman (2016) Text Book on Dynamic Relaxation Method. Lap Lambert Academic Publishing, Germany, and ISBN: 978-3-65994751-3.
12. Suleiman OME, Osman MY, Kassala S (2007)Deflection of Rectangular Laminated Composite Plates using Dynamic Relaxation Method, LAP LAMBERT Academic Publishing, Member of Omni Scriptum Publishing Group, Latvia, Germany. ISBN 978‐3‐330‐33164‐8.