Research Progress of Effective Stress and Effective Stress Equation

In 1920’s and 1930’s, Terzaghi presented the concepts of effective stress and the effective stress equation based on tests and engineering experience, which were concluded into the principle of effective stress by Jennings in 1961: firstly, effective stress equals total stress minus pore water pressure; secondly, the effective stress controls the strength and deformation of a soil. The principle of effective stress is considered the keystone of soil mechanics. Only with the concept of effective stress can we grasp the strength and deformation nature of a soil, establish the theory of strength and constitutive relationship of a soil, and thereby develop the theoretical system of Soil mechanics. Terzaghi’s principle of effective stress can only be applied to saturated soils. The application of this principle has achieved great success in soil mechanics and geotechnical engineering. However, since the physical meaning of the effective stress is still unclear, and the derivation of the effective stress equation lacks theoretical basis, there has always been controversial arguments about this theory since it was presented. The controversy focuses on what the effective stress is; whether the effective stress equation needs to be modified; and if there is the effective stress controlling shear strength and deformation for unsaturated soils. There are still no consensus on these issues among scholars till now. There are some main ideas about the essential nature of effective stress, such as inter-granular stress, skeleton stress, and equivalent stress that controls the shear strength and deformation of a soil. Lade and Boer gathered some of the effective stress equations for saturated. For unsaturated soils, because the effective stress equation has not been verified, some researchers believe that the strength and deformation of unsaturated soil cannot be characterized by a single effective stress. They must be characterized by different independent stress state variables [1].

The most important reason for the controversies surrounding effective stress lies in its unclear physical meaning. In 1996, Shao found that Terzaghi’s effective stress equation can be deduced by taking the pore fluid pressure and other external forces into account separately. He indicated that the effective stress is a kind of skeleton stress generated by all the forces excluding pore water pressure. In 1999, he deduced the effective stress equation for unsaturated soils in the same way, pointing out that the soil mechanics theory is applicable to both saturated and unsaturated soils. Subsequently, he and his students presented different ways to deduce the effective stress equation [2] and proved that, through tests and re-analysis of the test data published by other researchers, effective stress is the stress that controls the shear strength and volume change of a soil in unsaturated state.

The effective stress equation can be deduced by various methods through studying the effects of pore fluid pressure and other external forces on the soil skeleton separately [2]. Take unsaturated soils for example. On any plane at a point (REV) in the soil, the total normal force is equal to the sum of the normal force on the skeleton area generated by external forces excluding pore fluid pressure, the normal force generated by the pore fluid pressure, and the normal force on the void area generated by pore fluid pressure. The pore water pressure and pore air pressure acting on the skeleton area or void area can be determined by their respective volume fractions, as shown in Fig.1. Since the resultant force equals the sum of the component forces, the relationship between total stress, skeleton stress and pore fluid pressure can be obtained (Figure 1).

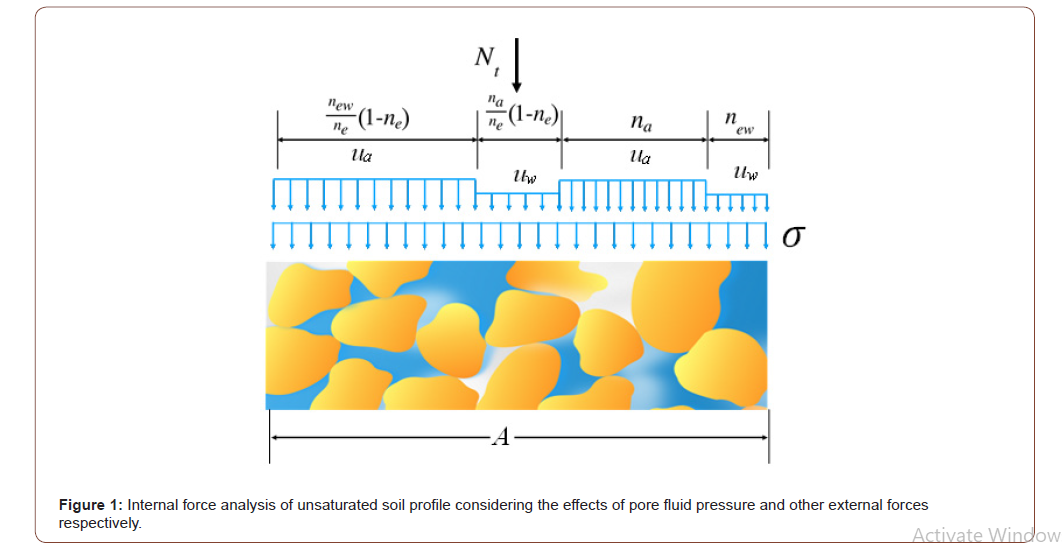
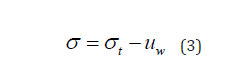
It can be seen that the effective stress is the skeleton stress due to external forces excluding pore pressure. Furthermore, the effective stress equation for a medium with multiphase fluids can also be easily deduced in this way.

For saturated soils, a large number of test and engineering practice repeatedly proved that the effective stress controls the shear strength and deformation. For unsaturated soils, Vanapalli et al. obtained an expression of shear strength based on the formula of shear strength expressed by double stress state variables and normalized the test results. Coincidentally it was shown that the effective stress controls the shear strength. Through tests and re-analysis of the test data published by other researchers, it is shown that: (1) the shear strength parameters and the effective stress of a soil in saturated state can be used to characterize the shear strength in unsaturated state; (2) under a same effective stress process, a soil both in saturated and unsaturated states produces same volume change.

The normal internal force on any plane of the soil is equal to the sum of the normal components. Because of the different properties and effects of the action, the normal internal force can be divided into the internal force generated by the pore fluid pressure and the internal force generated by other external forces. The relationship between resultant and component forces leads to the effective stress equation. Then some conclusion about the effective stress are as follows: Effective stress is the skeleton stress generated by external forces excluding pore fluid pressure; the relationship of the total stress, effective stress, and pore fluid pressure satisfies the effective stress equation, i.e. the effective stress is equal to the total stress minus the equivalent pore pressure. The equivalent pore pressure equals to the sum of the product of the fluid pressure and the volume fraction of each phase; when the effect of the pore fluid pressure on shear strength and volume change is negligible, the effective stress controls the shear strength and deformation.

This work is supported by National Natural Science Foundation of China (No. 51479023) and (No. 52079018).

No conflict of interest.

1. Lade PV, Boer R DE (1997) The concept of effective stress for soil, concrete and rock [J]. Geotechnique.
2. Shao L, Guo X, Liu S, Zheng G (2018) Effective stress and equilibrium equation for soil mechanics. CRC Press, Boca Raton.