Nonlinear Analysis of Local Corrugated Steel Shear Wall under Lateral Loading

One of the effective ways to improve the buckling behavior and increase the energy absorption capacity of steel shear walls is, installing stiffeners on them. The stiffener will increase the stiffness, ductility, energy absorption and sometimes resistance by preventing the buckling of the steel plate before its yielding. The presence of stiffeners as vertical, horizontal, or diagonal on the steel plate, results in the harder execution of welding and increased costs. In recent years, the use of corrugated steel shear walls has increase because of the high ductility that they provide, but the welding execution on the two edges of the corrugated plate to the frame is a challenging action. In addition, corrugates have a significant impact due to increasing the amount of steel consumed. In this paper the aim is seeking solutions to the problems mentioned above by using local corrugated plates. The local corrugated plate is a simple steel plate that is comprised of presses in vertical, horizontal, diagonal, or a combination of these configurations in specific distances. So far, no research has been done on the local corrugated steel shear walls, but similar research has been implemented to investigate the types of simple and corrugated steel shear walls, which will be investigated in the next section. In this research the target was to achieve higher resistance or more ductility compared to simple steel shear wall. This target was obtained by changing the shape and dimensions of the press and the thickness of the steel plate. Initially cylindrical corrugates under monotonic loading were modeled. In the next stage, trapezoidal corrugates under monotonic loading were modeled. Finally, both cylindrical and trapezoidal corrugates under cyclic loading were modeled. Literature review By comparing the analyzes of the equations devised for the overall buckling of the shear walls by researchers in the past, simple equations for overall shear buckling of corrugated steel shear walls were developed [1]. Using finite element analysis and testing, solutions for the design of rectangular diaphragms without openings were proposed [2]. Applying the analytical method of finite element, new relations were found regarding the improvement of the equivalent properties of anisotropic steel plate [3]. An analytical model has been presented for the in itial lateral stiffness of a sinusoidal plate under the effect of a combination of deformations caused by expansion, cutting and bending. The results of the analysis of this modeling show that in most corrugated plates, the lateral stiffness is less than that of simple plates which have the same thickness [4]. In experiments conducted, samples of beams with corrugated web were under shear loading and ruptured due to shear buckling. These samples were modeled using the finite element analytic method in Abaqus software and equations for determination of the shear buckling of the corrugated steel plate [5]. Research on the elastic buckling of stiffened and unstiffened corrugated plates using a mesh-free Galerkin method was taken from the first-order shear deformation theory. In this modeling, the corrugated plate is replaced with an anisotropic plate with uniform thickness and equivalent elastic properties. In the modeling of stiffened corrugated plates, these stiffeners are considered as beams, and then the total stiffness matrix of the structure is obtained by super imposing the strain energy of equivalent orthotropic plate [6]. Research on geometric parameters effective on buckling resistance and various modes of shear buckling (overall shear buckling and local shear buckling) of steel plates using numerical methods of finite element have been carried out. The results of this research were the formulation of equations for the shear buckling resistance [7]. Researchers investigated the inelastic buckling resistance of corrugated steel plates and provided equations in this regard [8]. An analysis of the mechanical properties of corrugated plates during expansion, free vibration and buckling was implemented. The results determined that an anisotropic model lacks enough accuracy in examining the torsional behavior [9]. Experiments were carried out on corrugated shear walls under cyclic loading and it was displayed that these types of shear walls have a high capacity in absorbing earthquake energy [10]. Investigations have been done on the cyclic behavior of simple steel plates and trapezoidal corrugated steel plates in vertical and horizontal directions. According to the results, the energy absorption capacity, the degree of ductility, and the initial lateral stiffness of the corrugated plates are higher than simple plates [11]. One experimental study has conducted on diagonally stiffened steel shear wall with central opening. Their results indicate that structural properties of the perforated wall are improved using diagonal stiffeners. The ductility of the perforated system is 14% greater than un-stiffened solid model [12]. Research has been conducted on the nonlinear behavior of corrugated steel shear walls, and the results show that the trapezoidal corrugated plates have an energy absorption capacity, ductility, and higher final load capacity compared to sinusoidal corrugated plates [13]. The corrugated plate is modeled using the variational asymptotic method and equations for the effective stiffness of thin and thick corrugated plates was presented [14]. The elastic shear buckling behavior of corrugated trapezoidal plates alongside vertical stiffeners was modeled via applying the Ritz method and Minimum Potential Energy potential theory. From the results of this research, the equations determining the buckling loads of this type of plates were presented [15]. Research has been carried out on the elastic shear buckling behavior of the sinusoidal corrugated steel shear walls and by applying the finite element method in Abacus software, equations are presented for determining the buckling shear loads of sinusoidal corrugated plates [16]. In one research ultimate strength of shear wall with opening was investigated. Their results showed that shear strength decrease when cutout provide at the center and that increase by providing stiffeners around the cutout [17]. In other research, strength equation for corrugated steel shear walls with reduced beam section was proposed [18].

Initially the proposed design must be verified through creating a model in Abacus. First a simple steel shear wall is modeled according to an article by Alavi and Nateghi (2013) in the Abacus software [12]. In the next step a localized corrugated steel shear wall is modeled. The outlines of the model for the simple shear wall are displayed below; The height of the shear panel is 1.5 and its length is 2 meters, l/h=1.33. These dimensions correspond to are designed according to AISC344-05.Figure 1shows the steel shear wall panel. The mechanical properties of a medium-sized shear wall with a true width of 3 and a length of 4 meters is displayed. The beam and frame column properties of steel materials from tension Coupon test according to ASTM370-05 is displayed in (Table 1).

In the modeling, the displacement and rotation movement out of plan are restrained. The profile of the steel used in the modeling is given in (Table 2).

An isotropic model under controlled displacement condition ̶ defined as a displacement up to a specific level (70 mm) ̶ is implemented, and corresponding to that, the amount of force is recorded. To prevent stress concentration in the point of displacement, a rigid plate is welded on the top right area section of the wall (to the upper beams), and the displacement is applied to the plate in the software. The lower flange of the bottom beam is restrained in terms of displacement and rotation (rigid support) (Figure 1).

Additionally, the displacement and rotation out of plan is also restrained. Outputs derived from this modeling are based on nonlinear buckling analysis and implicit solution method according to New Mark algorithm. The loading procedure is initially monotonic and in the two final models is cyclic (similar to the loading of the earthquake). The type of element used to mesh is a 4node- 2D (181) with six degrees of freedom and a dimension of 3.5 cm. Meshing in a simple steel shear wall model is structured. The stress-strain graph is obtained from a nonlinear static analysis based on Von Mises submission to stress. In case of creating the hysteric curve, a quasi-static analysis is used, therefore the frequency of the period is chosen arbitrarily, and the change in the value of T will not affect the results. The initial and final resistance in the load-displacement curve under uniform displacement can be easily verified, but some parameters such as the ductility and energy absorption of the hysteric curve as well as the relationships presented in previous studies can be estimated. First, the accuracy of the models of the monotonic and cyclic curves were confirmed and can be displayed in Figures 2, 4 (panel 2 belongs to the verification paper) (Figure 2-4).

Subsequently, different models of presses at varying intervals, with different dimensions in plan and out-of-plan in a steel plate with varying thickness were designed. Table 3 displaced the different tests implemented on the model (Tables 3).

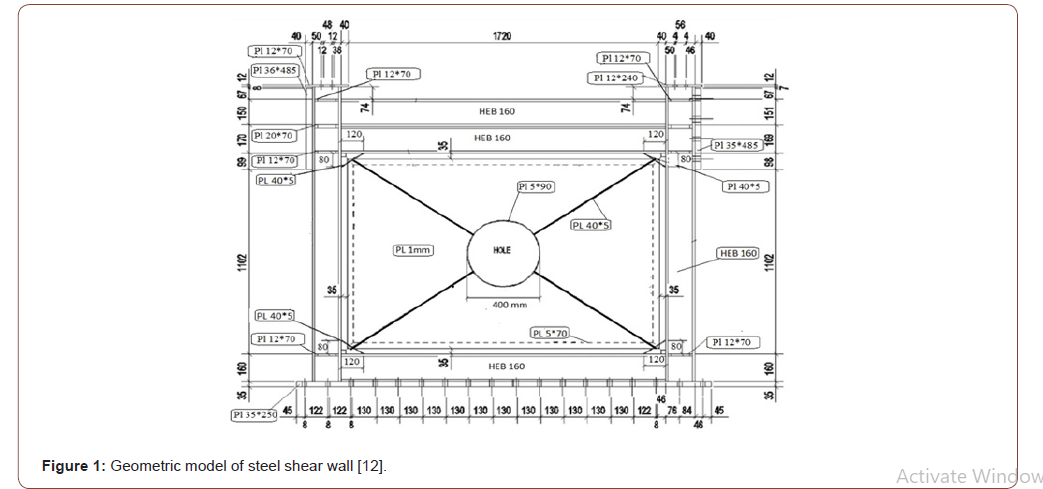
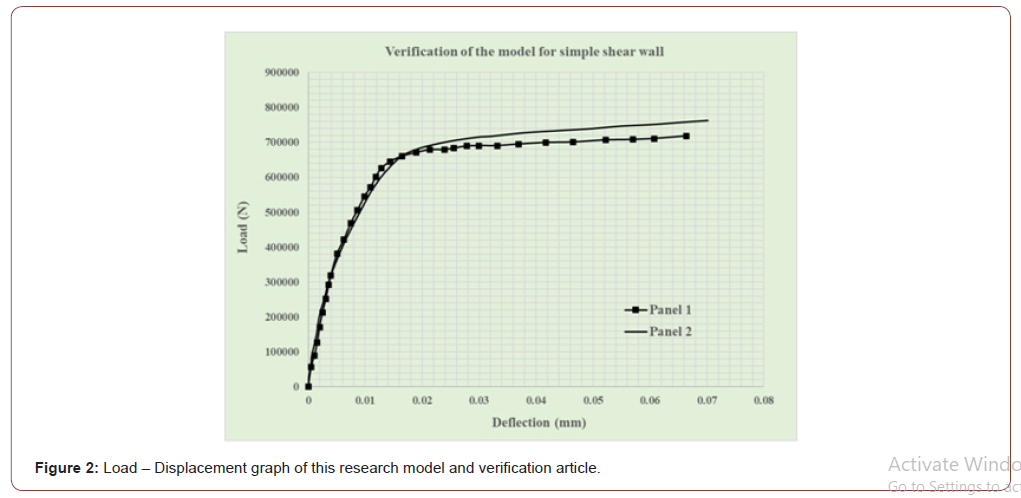
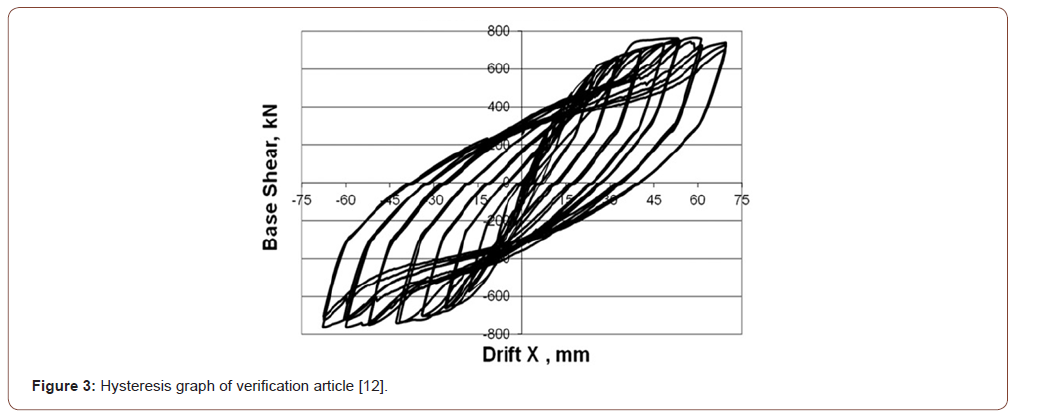
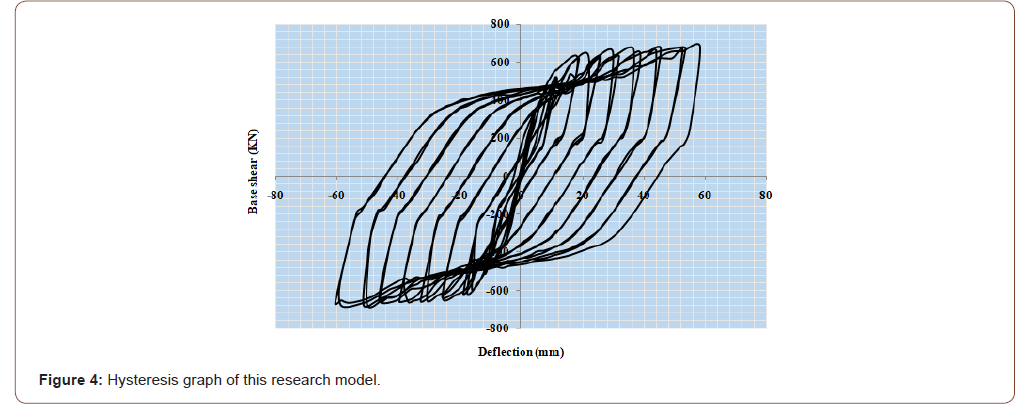
Table 1:Mechanical properties of frame steel [12].

Table 2:Steel plate specifications [12].

Table 3:The test implemented on the model.

Local cylindrical pressed steel shear walls

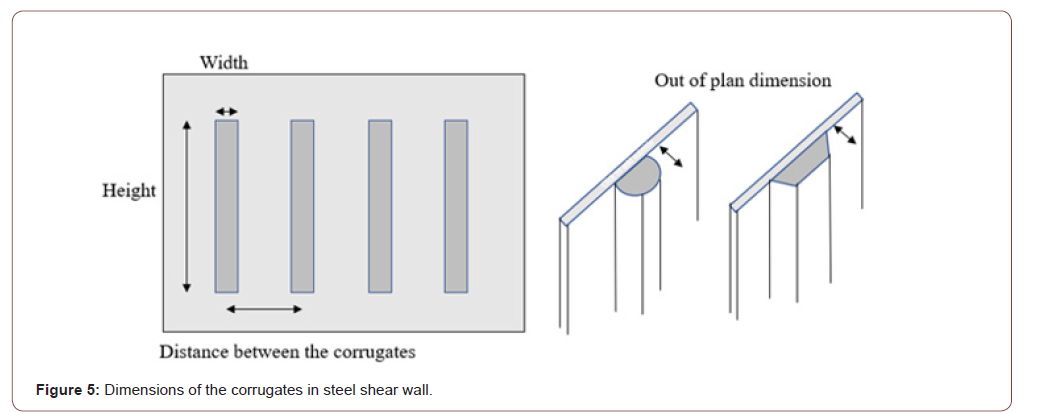
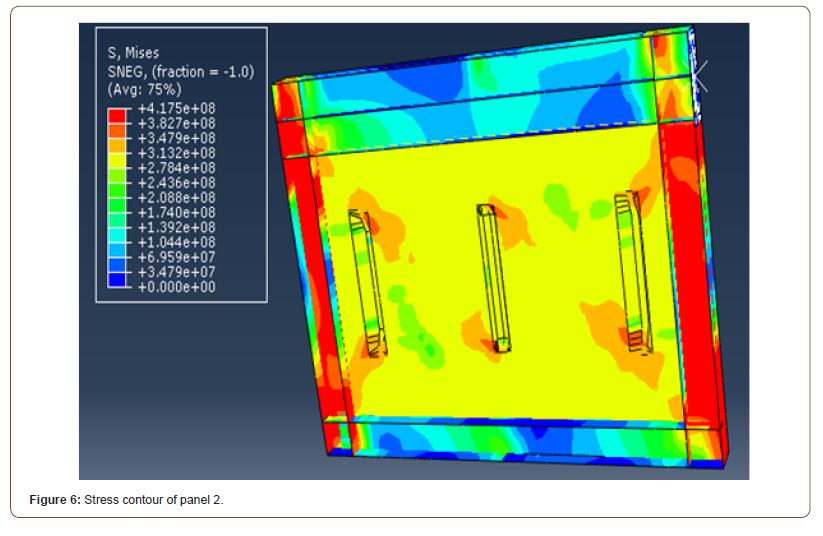
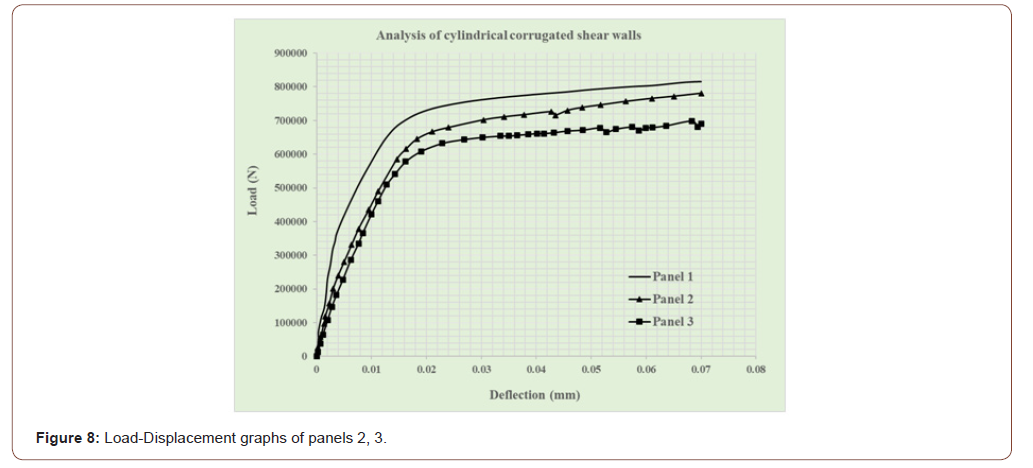
Since in very low thicknesses (less than 1 mm), the presence of presses has a small effect on the degree of resistance and ductility, therefore the modeling can start at a thickness of 1 mm. Initially, cylindrical presses in horizontal and vertical modes in the arbitrary dimensions was created. Panel 1 refers to the simple steel shear wall (in all off models) and the characteristics of panels 2 and 3 are according to Table 4. Figures 6 and 7 are displayed the stresses in these two new models. Based on the obtained graphs, as can be seen in Figure 8, it can be concluded that the horizontal presses had better performances compared to vertical presses, but still have not achieved the shear strength of the simple steel shear walls (Table 4 and Figure 6-8).

Table 4:Press dimensions of panel (1 mm thick).

Table 5:Press dimensions of panel in frame with strong columns (9 mm thick).

Table 6:Presses dimensions in steel plates (thickness 6 and 9 mm).

Table 7:Ductility Factors.

Table 8:Corrugated shear walls models (6 mm thick).

Local trapezoidal corrugated steel shear walls

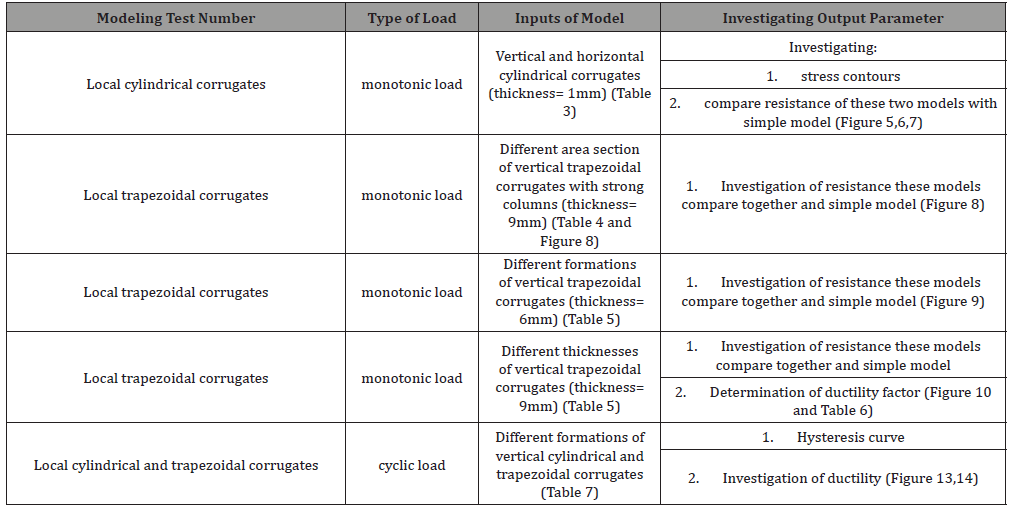
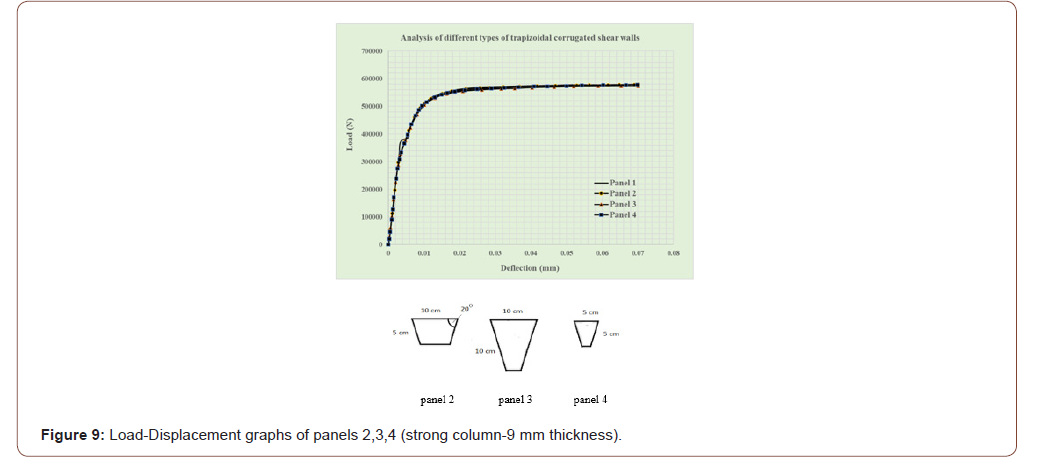
Local trapezoidal corrugated steel shear walls with strong columns: Horizontal presses are also not economical because of the higher consumption of steel, thus reinforcement of the columns and the use of trapezoidal presses (in high thickness plate) was considered. From Table 5andFigure 9,it can be concluded that different local corrugated types of cylindrical corrugated steel walls yield different dimensions (within the same shape e.g. trapezoidal/ circular) has little influence on resistance of steel shear wall at 9mm thickness of panel. The parameters displayed in the results are listed below and (Figure 5).

N: number of press

D(cm): height trapezoid

W(cm): press width

H(cm): press height

(Table 5 and Figure 9)

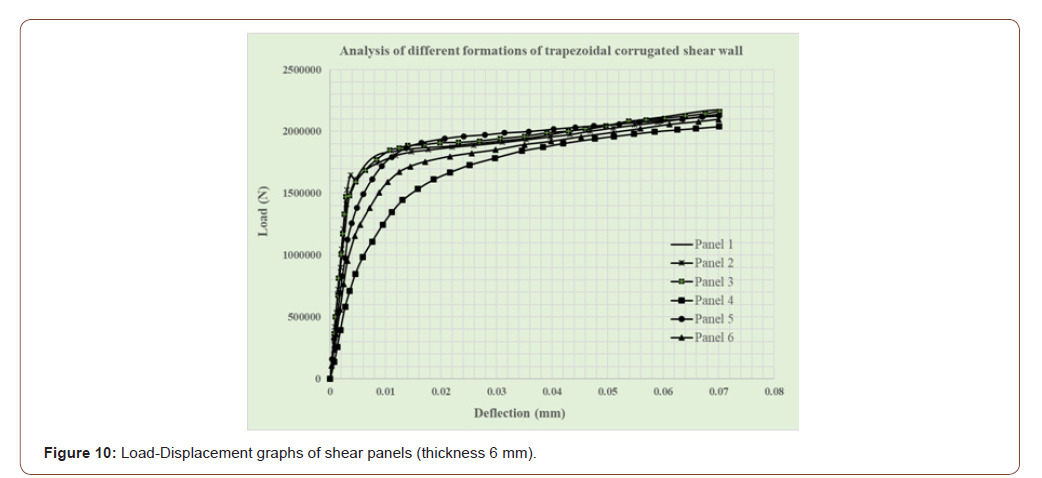
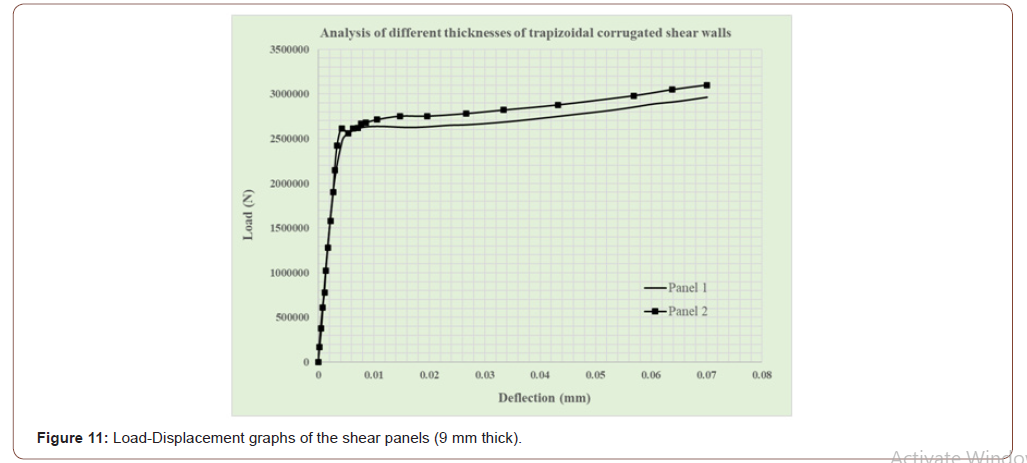
Different formation of Local trapezoidal corrugated steel shear walls: In the next step, other types of pressed trapezoidal steel shear walls with a thickness of 6 and 9 mm, were created, which had a change in the width of the press, the spacing between presses and the number of presses. The geometric characteristics of the presses created are displayed in Table 6. Presses dimensions in steel plates (thickness 6 and 9 mm)and the resulting graphs are shown in Figure 10and 11. The results for 6 mm steel shear walls indicate that the existence of more presses with less widths has a positive effect on the final resistance compared to lower number of presses with longer widths. As can be viewed in the next diagram, panel 2 in, with a thickness of 9mm, has a larger resistance compared to the shear strength of a simple steel with the same thickness (Table 6 and Figure 10,11).

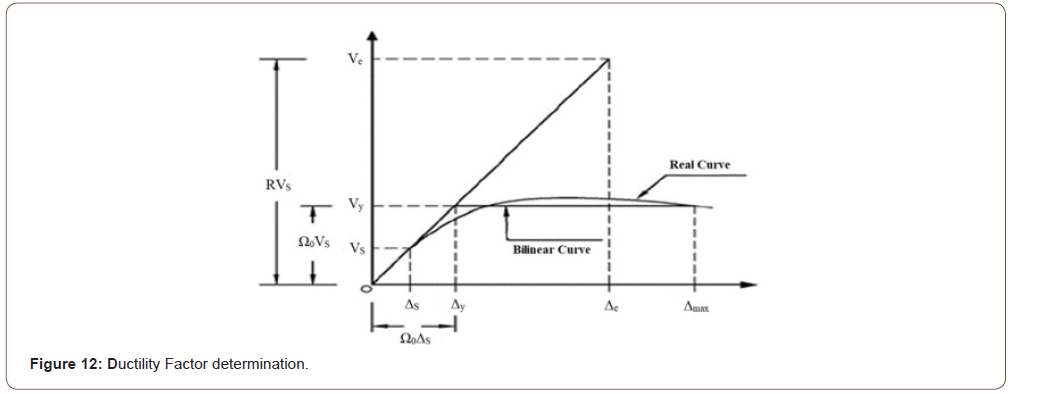
Ductility factor(R)

The behavior factor is calculated according to the equation 1:

Reduction factor(Rμ): Due to the ductility, the building will have a capacity for the depreciation of hysteric energy. Reduction Factor of the Strength is found by dividing the value of elastic strength by the yield strength. It is displayed in equation 2.

Structural ductility factor (μ): This factor is taken as the ratio of the maximum displacement that can be reliably sustained without significant strength loss to the displacement where significant inelastic displacement starts to occur. It is displayed in equation 3.

Over strength factor (Ω): The storage resistance which is between the overall yielding of the structure (and the initial yield level) exists which is known as over strength. Accordingly, the coefficient of over strength, is equal to the quotient of the division of the force (corresponding to the overall structural yielding of the structure during the formation of the failure mechanism), to the force corresponding to the formation of the first plastic joint in the structure. It is displayed in equation 4.

Allowable stress factor (Y): This coefficient is determined according to the approach of the construction material manuals with design stresses (allowable or ultimate load) and its value is: the ratio of the force required for the formation of the first non linear joint to the force limited to allowable stresses. The range of this factor is about 1.4 to 1.5 According to Table 7, which has been obtained from the load-displacement of panel 2 (thickness 9 mm), considering Figure 12and the presented relations, it was understood that the energy absorption of the local trapezoidal corrugated steel shear wall in this state is more than the simple steel shear wall. Since the attribute of energy absorption in steel shear walls is more important than the lateral resistance, thus, local corrugated steel shear wall in certain states has a better performance than the simple type and can be applied easily (Figure 12 and table 7).

To better understand the energy absorption, we put two the final models under cyclic loading. The displacement to the cycle’s number diagram is shown in Figure 13. In order to draw the hysteric curve in Abacus software, it is necessary to have a displacement- time graph. Dimensions of the local corrugates are given in Table 8. The hysteric diagrams are shown in Figure 14 and 15. The results show that with regard to the fact that the area inside the hysteric curve is related to a local trapezoidal steel shear plate model, which is more than the area inside the hysteresis of the simple steel shear wall, thus, it has more energy absorption capacity. Therefore, it was revealed that the energy absorption of the local cylindrical corrugated shear wall does not have a major different from the steel shear wall (Table 8 and Figure 13-15).

The aim of this research was determination of shear resistance and ductility in local corrugated steel shear walls by placing them in a specified frame under controlled-displacement conditions. Considering the numerous variations possible for local corrugated plates, in this research some of the variations were investigated. Regarding the load-displacement diagrams, under uniform and cyclic displacement of the models created, it was concluded that in the thin corrugated steel shear walls (0.8 and 1 mm), the presence of local presses has practically no positive effect. As pointed out in previous studies, trapezoidal shaped presses have higher resistance and ductility compared to cylindrical presses, especially in the vertical mode. In shear wall with a large thickness (6 and 9 mm), the existence of vertical trapezoidal presses is preferred to cylindrical presses of the same thickness. Additionally, the resistance of the shear wall has a direct correlation with the number of presses, and reverse relation with width and out of plan dimension of trapezoidal corrugates in steel shear wall, spacing between the presses. The reinforcement of the columns contributes to the adaptation of the load-displacement diagram (under the lateral loading of the steel shear wall, which has a trapezoidal press in the middle of the wall’s panel) with a simple shear wall. It can be concluded that the rigidity of the columns, leads to a better understanding of the behavior of the steel plate. In this type of shear walls, increasing the number of presses increases the initial resistance and reduces the ultimate resistance. According to the hysteric curves, the local trapezoidal corrugated steel shear wall has a higher energy absorption than a simple steel shear wall. In steel shear walls, the degree of energy absorption and ductility has more importance compared to resistance. Therefore, the use of these steel sheets in the construction of shear walls in terms of the shape and strength (in certain conditions) is recommended. Since only some types of local corrugated steel shear walls were investigated, future research of this study can be dedicated to investigation of types of local corrugated shapes with different plate thickness and different arrangement. Models under cyclic loading must be developed to better understand the results. The results of this research can be applied for designing without stiffeners, reducing welding area and increasing ductility in steel structures.

None.

No conflict of interest.

1. Easley TJ (1975) Buckling formulae for corrugated metal shear diaphragms. Structural Division 101(7): 1403–1417.
2. Davis JM (1976) Calculation of steel diaphragm behavior. Structural Division ASCE 102: 1411–1430.
3. Briassoulis D (1986) Equivalent orthotropic properties of corrugated sheets. Computers and Structures 23(2): 129–138.
4. Shimansky RA, Lele MM (1995) Transverse stiffness of a sinusoidally corrugated plate. Mechanic of Structures and Machines 23(3): 439–451.
5. Driver RG, Abbas HH (2006) Shear behavior of corrugated web bridge girders. Structural Engineering ASCE 132(2): 195–203.
6. Liew KM, Peng LX (2006) Buckling analysis of corrugated plates using a mesh-free Galerkin method based on the first-order shear deformation theory. Computational Mechanics 38: 61–75.
7. Yi J, Gil H, Youm K (2008) Interactive shear buckling behavior of trapezoidal corrugated steel webs. Engineering Structures 30: 1659–1666.
8. Eldib MEA (2009) Shear buckling strength and design of curved corrugated steel webs for bridges. Constructional Steel Research 65: 2129–2139
9. Wennberg D, Wennhage P (2011) Orthotropic models of corrugated sheets in finite element analysi. ISRN Mechanical Engineering.
10. Emami F, Mofid M (2013) Experimental study on cyclic behavior trapezoidal corrugated steel Shear walls. Engineering Structures 48: 750–762.
11. Shimizu N, Kanno R (2013) Cyclic behavior of corrugated steel shear diaphragms with end failure. Engineering structures 139(5): 796–806.
12. Alavi E, Nateghi F Experimental Study on Diagonally Stiffened Steel Plate Shear Walls with Central Perforation. Constructional Steel Research 89: 9-20.
13. Edalati SA, Yadollahi Y (2014) Numerical study on the performance of corrugated steel shear walls. Wind and Structures 19(4): 405–420.
14. Ye Z, Berdichevsky VL (2014) An equivalent classical plate model of corrugated structures. Solids Structures 51(11): 2073–2083.
15. Tong JZ, Gue YL (2015) Elastic buckling behavior of steel trapezoidal corrugated shear walls with vertical stiffeners. Thin-Walled Structures 95: 31–39.
16. Dou C, Jiang ZQ et al. (2016) Elastic shear buckling of sinusoidally corrugated steel plate shear wall. Engineering.
17. James J, Kumar AS (2016) Corrugated steel plate shear wall with opening and stiffener at opening. J Science and Research.
18. Farzampour A, Mansouri I (2018) Analysis and design recommendations for corrugated steel plate shear walls with a reduced beam Section. Thin- Walled Structures 132: 658-666.