Innovative Spatial Cross System Cable Arrangement for Seismic Response Mitigation of Cable-Stayed Bridges

Cable-stayed bridges are the most practical and economical solution for the span lengths ranging from about 200 to over 1000 meters [1]. Despite the popularity of cable-stayed bridges in recent decades, research about their seismic behavior is still ongoing. The role of the cables with distinctive architecture and nonlinear behavior leads to the complexity of seismic behavior in both the lateral and longitudinal directions. Due to high construction and maintenance expenses of such bridges, the need for further research about the seismic behavior and its improvement is obvious. Both dynamic and static response of cable-stayed bridges have also been addressed by many studies since the early 1980’s [2-7]. Karoumi [8] investigated modeling techniques for the stay cables under dynamic moving loads. Kawashima & Unjoh [9] showed the importance of damping and complications related to its estimation originating from the cable-stayed bridge elements (towers, cablesystem and deck), their configuration and interactions between the elements. Fleming & Egeseli [10] discussed the dynamic response of a cable-stayed bridge to seismic, wind and simulated traffic loads. They considered non-linear behavior of the cables and concluded that the non-linearity of the cable-stayed bridges must be considered in determining the stiffness of the structure, even under static gravitational loads. Abdel-Ghaffar [11] and Abdel-Ghaffar & Khalifa [12] studied the dynamics of cable-stayed bridges with special attention to nonlinear behavior, the sensitivity to support conditions, cable-vibration phenomena and spatial variability. Wilson & Walker [13] investigated natural modes of vibration of cable-stayed bridges, through numerical analyses. Bruno & Leonardi[14] also studied the lateral and torsional vibration modes of cable-stayed bridges. They observed small contribution of the minor deck stiffness and the tower shape to flexural oscillations, with the exception of torsional modes, which were considered clearly affected by afore-mentioned factors. He et al [15] considered semi-active damper, passive viscous and constant friction dampers between deck and bridge pylon to mitigate seismic response of a cable-stayed bridge. They showed that the type of the connection between the deck and the towers is a key factor in the static and dynamic behavior of cable-stayed bridges. The case-studies of Fujino & Siringoringo [16] about Yokohama Bay bridge (Japan), Liu et al [17] about Hangzhou bridge (China), Morgenthal [18] about Rion Antirion bridge (Greece) and Nazmy and Abdel-Ghaffar [19] considered the effect of different deck to pylon connections as well as two extreme cases of floating and fixed connections. As a new proposal, innovative using of spatial cable-system for seismic response mitigation and rehabilitation of cable-stayed bridges is investigated in this paper. The idea came from the system with two transversally inclined cable planes, which is used in some pipeline bridges (e.g., the bridge across the Labe River in the Czech Republic) as shown in Figure 1 [20]. The main purpose of this study is to investigate the effect of supplementary spatial cable system on the seismic performance of cable-stayed bridges. The seismic consequences of different spatial cable-system arrangements considering key parameters like the main span length and deck to pylon connection are investigated. Among possible spatial cablesystem configurations, it is found that the cross-system cable arrangement has a better performance in mitigating lateral and longitudinal seismic responses of the deck. In addition, the crosssystem arrangement is effective in improving the longitudinal seismic response of the pylons (Figure 1)

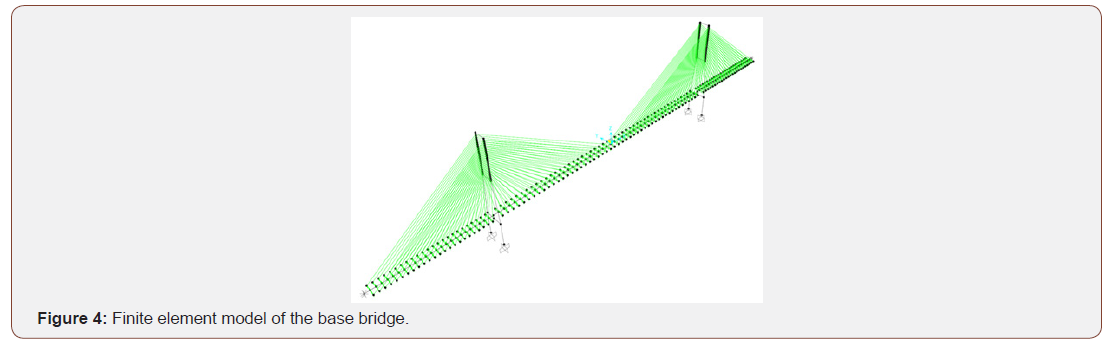
Detailed review of the section dimensions and proportions of several constructed cable-stayed bridges was performed to establish the base models for this study. The main span, as the key parameter defining the dimensions of the rest of the bridge, was considered as 300,400 and 500 meters. The models were assumed to have two H-shaped towers, as most of the constructed cablestayed bridges do. These models herein are named the base models and are designated as H300, H400 and H500, which have no spatial cable arrangement. The deck was assumed to hold four traffic lanes with a total width of 22 meters. The cross section of the deck for all bridge models was considered the same as that assumed by Pedro et al [21]. It consisted of a 0.25 m thick slab in composite action with two 2.5 m deep steel girders at two sides and steel cross-girders spaced at 10 m supporting the slab together with steel subsidiary beams. Figure 2 demonstrates a schematic 3D view of the deck elements. Figure 3 represents the schematic model of the considered bridges. Based on the review of constructed bridges, the height of the tower above the deck was considered to be 0.3 times the main span length and the height of tower below the deck was assumed to be 50 meters. The main cables were considered to have semi-fan configuration, which connect the whole length of the deck to the upper half of the towers. Post-tensioned multi-wire helical strands with total area of 19.6 cm2 were considered as the main cables. Nonlinear cable elements were used for modelling cables. The cable elements were assumed to be capable of withstanding tensile forces only and cannot carry compression. Figure 4 represents the finite element model of the H400 base bridge. The type of the connection between the deck and the pylons has major effects in the seismic behavior of cable stayed bridges. The constructed cable-stayed bridges in seismic areas usually possess deck to tower connections that are different from the usual floating connection. In the floating type of connection, the deck is free to move in the longitudinal and lateral directions and rotate in torsional mode. Hence, no reaction is directly exerted to the tower under lateral earthquake forces. In this connection, the displacement of the deck is partially constrained between both towers, by cables. In the restrained connection system, the longitudinal, lateral and torsional degrees of freedom are considered to be fixed between the deck and the tower. However, the rotation about the longitudinal and transverse axes of the bridge are released. In this study, the restrained type of deck to tower connection was employed in the base models (Figures 2-4).

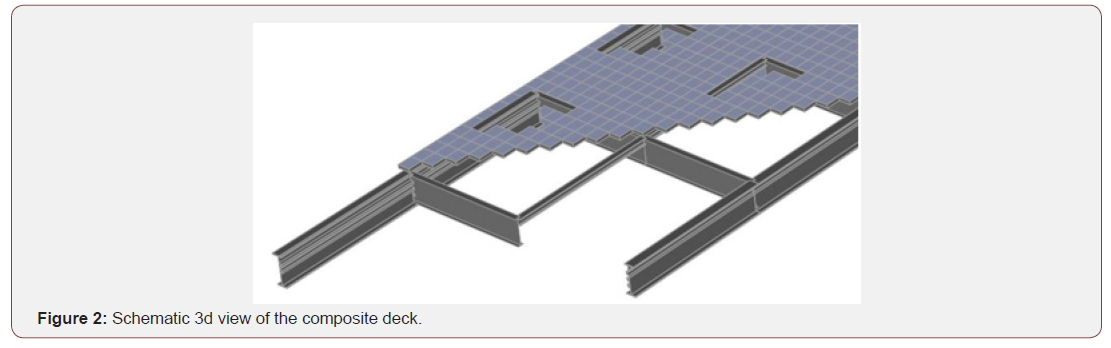
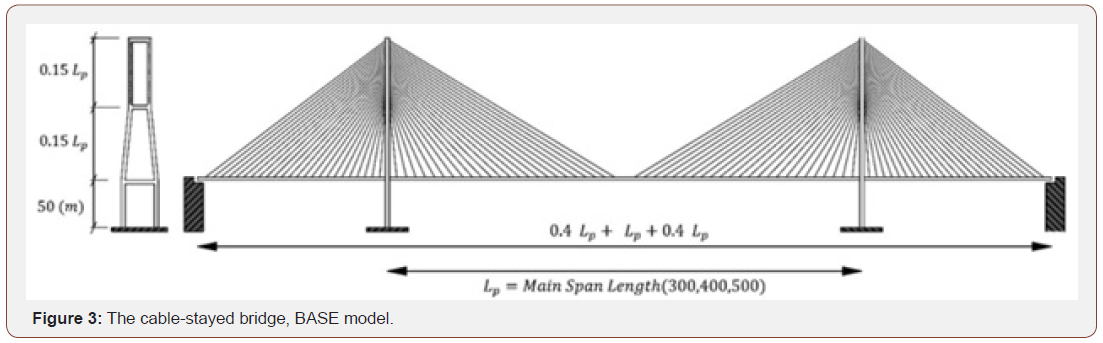
Spatial lateral cable system

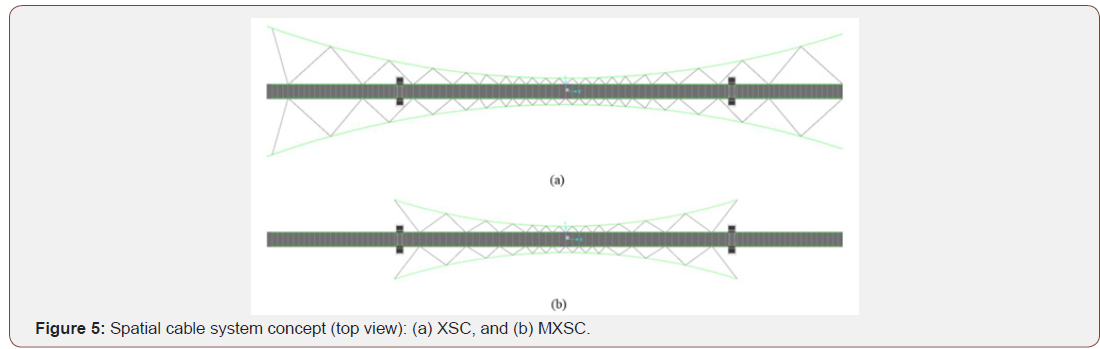
A solution to the problems associated with lateral loads on cable supported bridges with long and slender spans is to modify the cable system so that it can resist not only vertical, but also lateral loads. As an innovative solution, a new spatial cable system is proposed herein, similar to the spatial cable systems, which have been already used in pipeline bridges [20] (see Figure 1). Two transversely inclined main cables have been considered on either side of the cable-stayed bridges to improve the seismic performance of such bridges. To achieve reasonable seismic performance, it is crucial to use cross-type cable system to connect the deck to the main spatial cables. The pretension force in the cross-type cables give a curved shape to the main spatial cables. Post-tensioned multi-wire helical strands of total 78 cm2 with arc curvature of 8% and 15% in horizontal inclination are used to model the main spatial cables, in all span lengths. Two spatial cable systems are proposed, as illustrated in Figure 5, namely ‘XSC’ and ‘MXSC’ systems. The XSC system consists of a cable-stayed bridge (base model), in which only the longitudinal constraints connecting deck to towers are released completely, supplemented by spatial lateral cables through the whole length of the deck, and anchored in the abutment foundations. The MXSC system consists of cable-stayed bridge base model, in which all longitudinal, lateral and torsional constraints connecting the deck to towers are released completely, supplemented by spatial lateral cables covering the distance between the pylons and anchored to the pylons foundations. These bridge models are compared with the base model having no spatial cable system with fixed deck to tower connection. Also, another version of the base model (called NLT model) in which the lateral and torsional constraints of the deck to towers are released are considered to investigate the effects of deck-pylon connection type on the transverse responses (Figure 5).

Modal analyses of the bridges

Modal analyses were performed on the bridge models in order to investigate the basic dynamic characteristics of the bridge models. Different boundary conditions associated to deck-pylon connections and supplemental spatial cable system resulted in significantly different structural dynamic characteristics.

Figure 6 illustrates the accumulated modal mass participation of the first 100 modes of vibration for the bridge models. In both longitudinal and lateral directions, 100 modes are sufficient to achieve accumulated modal mass participation of approximately 1.0. As it can be clearly seen from Figure 6a, the longitudinal diagrams for cable-adjusted models have absolutely higher participation ratio for first modes with higher vibration period. Therefore, the response of these systems is more dependent on their primary modes, which are mainly deck-activated mode shapes. In addition, models with spatial cable system have lower periods for fundamental lateral modes of vibration, especially in the bridges with lower span lengths. Because the deck has a relatively small mass compared to the whole structure, especially in shorter span bridges, the total mass participation of the deckactivated modes is relatively small. Besides, tower-activated modes remained almost unchanged after using the spatial cable system with different cable arrangements. The first transverse vibration mode in NLT model mainly involves the deformation of the deck, but in the base model it also excites the towers in the transverse direction. So, it can be concluded that transverse deck to pylon connection causes significant difference in dynamic response. The deck-activated modes have higher periods and are also sensitive to different cable arrangements. The first dynamic modes which have the most mass participation are usually considered as the basis for seismic investigation of bridges (Figure 6).

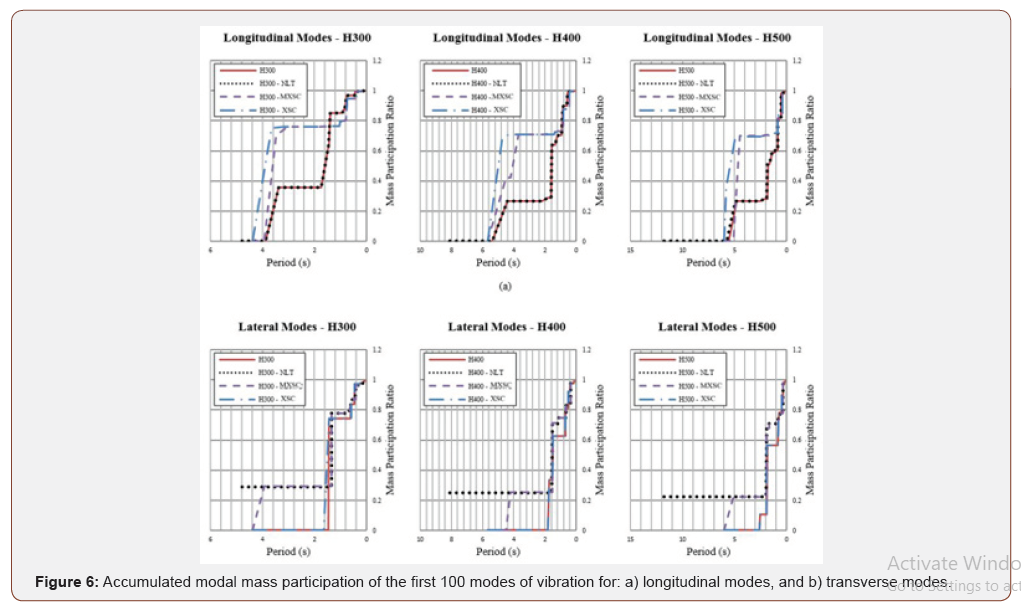
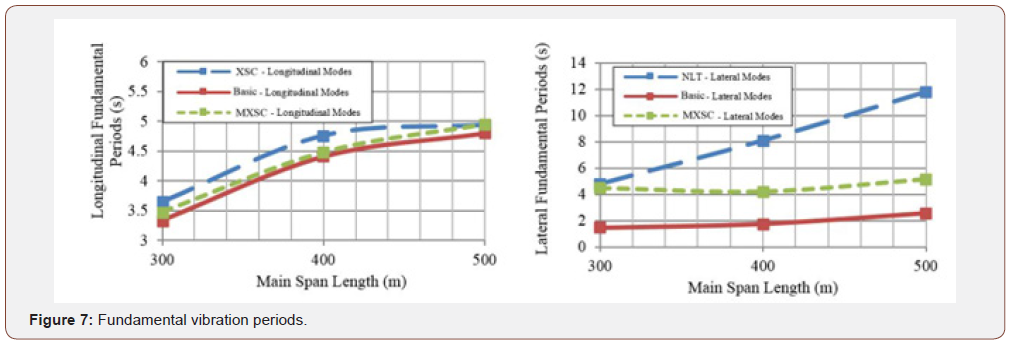
Figure 7 represents the periods of the fundamental mode of vibration of the cable-stayed bridges for different span lengths, in the longitudinal and transverse directions. As one can understand from this Figure, the spatial cable system arrangement and deckpylon connection play a major role in defining the natural period of vibration. In the longitudinal direction, releasing the deck-pylon connection leads to an increased main longitudinal vibration period beyond the practical range. On the other hand, using the mentioned spatial cables decreases the vibration period. In order to obtain the required characteristics for spatial cables and their arrangements, an iterative analysis was performed until the resulting vibration period for main longitudinal mode reaches at the proximity of that of the base model. In the transverse direction, releasing the mentioned connection (as seen in NLT models) leads to an increased main transverse vibration period beyond the practical range. It is observed that the MXSC system reduces the inappropriately high lateral period, caused by releasing the lateral deck to pylon connection in NLT models (Figure 7).

Seismic analysis parameters

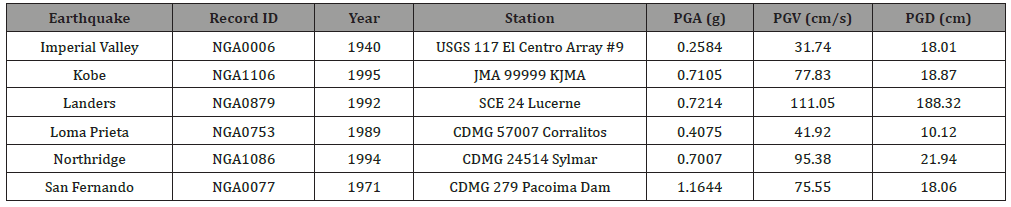
In order to evaluate the seismic behavior of the cable-stayed bridges, elastic nonlinear step-by-step direct integration timehistory analyses were performed under six scaled ground motion records, considering large deformation effects. The characteristics of the six seismic excitations are listed in Table 1. The longitudinal and transverse earthquake excitations were considered simultaneously in the analysis of bridges. The stronger of the two horizontal components of every strong motion was considered along the bridge longitudinal axis and the other component in the transverse direction for the LTH models. In the TTH models, the stronger of the two horizontal components of every strong motion was considered along the bridge transverse axis and the other component in the longitudinal direction. All earthquake loads were exerted to the structure after the deformed state of nonlinear static case due to gravity loads. Scaling of time histories were done according to ASCE 7-10 (ASCE, 2010). In the time domain, each ground motion was scaled such that the average square root of sum of the squares (SRSS) of the 5% damped response spectra of the two horizontal components of the ground motion does not fall below the 5% damped design spectrum in period range between T0 and Tn . Values of T0 and Tn were considered as 0.2T and 1.5T, where T is the fundamental period of the structure in the direction of the stronger component of the ground motion. Design response spectrum used for scaling the time histories was taken from LRFD Bridge Design Specifications (AASHTO, 2010), which is shown in Figure 8. Precise estimation of inherent damping in cable-stayed bridges is very complicated. It depends on the structural elements, cables, connections and the interaction among them. Rayleigh damping with ζ=2% for frequency of the main modes of vibration in the longitudinal and transverse directions, was considered in the time history analyses. In this method, damping varies with the frequency; and it considers higher damping ratio for higher modes of vibration. It should be noted that the nonlinear cable effects arising from the cable sag have been taken into account in the analyses (Table 1) (Figure 8).

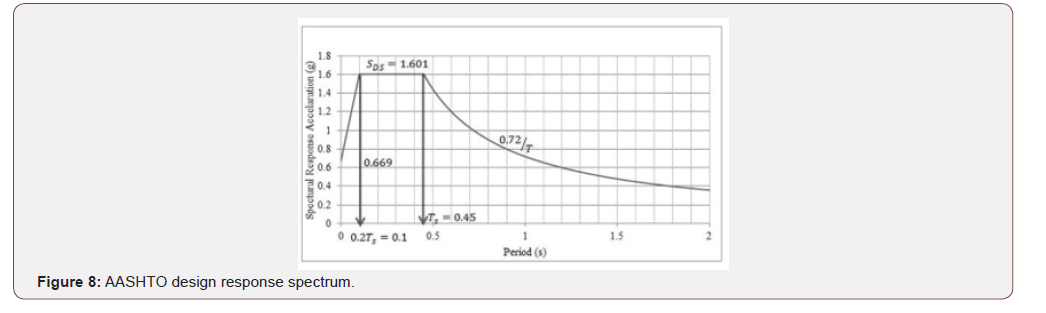
Table 1: Specifications of the selected ground motions.

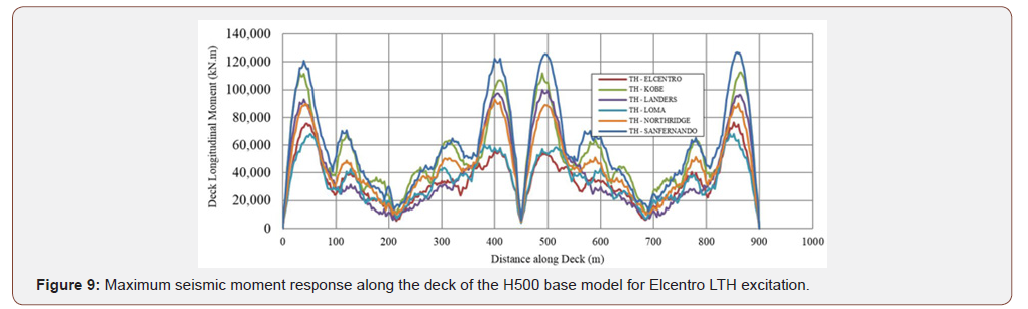
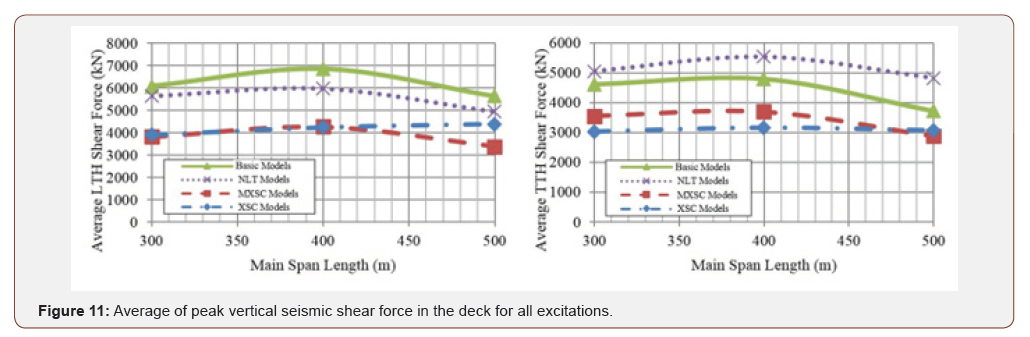
Figure 9 shows the distribution of absolute maximum seismic longitudinal moment response along the deck, for the base H500 model, under the 6 scaled ground motion records. As it could be seen from the moment distribution, the maximum moment occurs approximately at the locations with the highest cable inclination, or as one can say, at the farthest cable connection to the deck from the pylons. Figure 10 demonstrates the peak seismic longitudinal deck moment, under the LTH and the TTH excitations. As can be seen from the Figure 10, using the spatial cable system with MXSC and XSC configurations, decreases the deck seismic longitudinal moment response by about 47%, as an average. The main reason for this is the inclination of the spatial cables plane from the horizon line which provides the deck with additional vertical and longitudinal stiffness. Figure 11 shows the peak seismic vertical shear in the deck, averaged over all seismic excitations considered in the analyses, for the LTH and the TTH cases. As one can see from Figure 11, the deck shear force reduces by almost 30%, using spatial cable arrangement in both MXSC and XSC configurations. That is because the spatial cables carry some of earthquake-induced loads in axial action, hence reduce the deck shear demand (Figures 9-11).

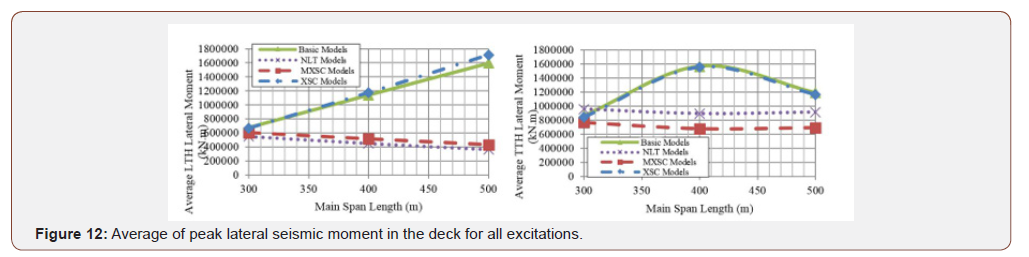
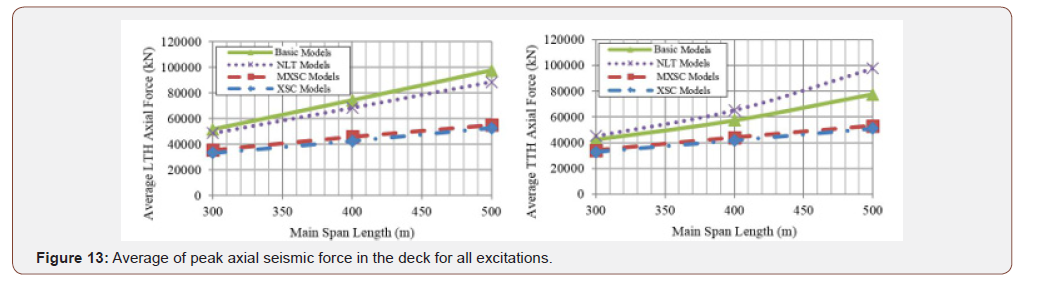
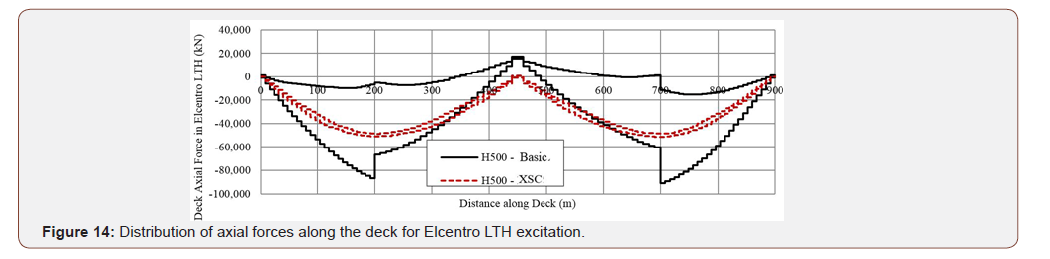
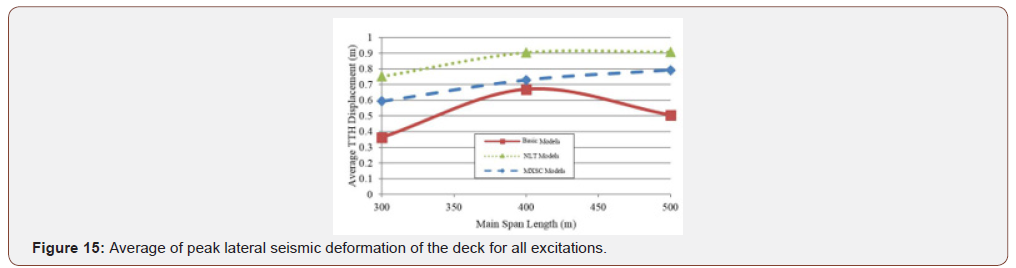
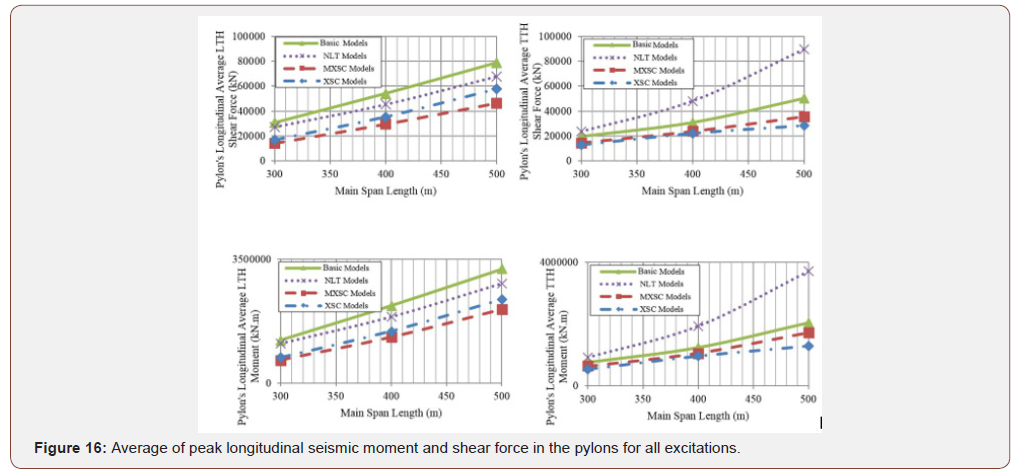
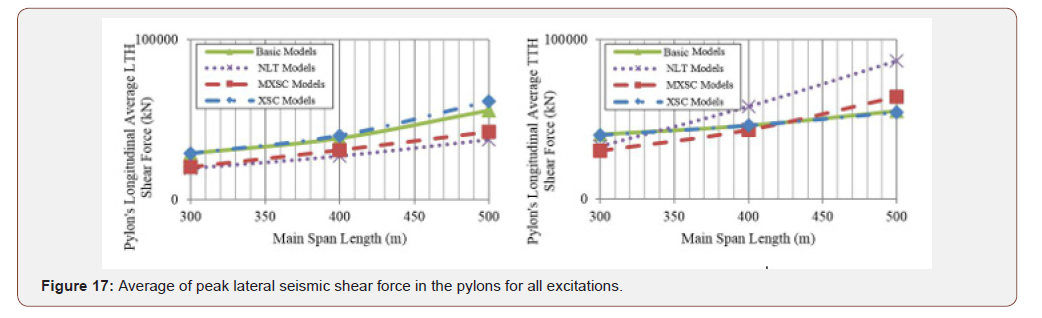
Figure 12 shows average of maximum seismic lateral moment in the deck for all excitations in terms of main span length, for all models under LTH and TTH cases. As shown in the Figure , the NLT and XMSC models, in which the lateral and torsional deck to pylon connections are released, demonstrate lower lateral moments; especially in bridges with longer spans for LTH records and in bridges with medium span range for TTH records. Likewise, the base model and the XSC model which contain restrained lateral and torsional deck to pylon connections have similar lateral behavior. Therefore, it can be concluded that the effect of deckpylon connection type is more significant in the lateral behavior of cable-stayed bridges, than the spatial cable system existence and type. It should be noted that no advantage observed in XSC models regarding to lessening the lateral deck moment, especially in LTH cases. Figure 13 illustrates the maximum seismic axial compressional force in the deck, averaged over all the excitations, for all models in terms of main span length, for the LTH and the TTH records. The Figure s show the spatial cable system in both MXSC and XSC models, obviously decreases the axial deck forces under both the LTH and TTH records. Figure 14 demonstrates the distribution of maximum and minimum axial force along the deck for H500 model with and without spatial cable system under El Centro LTH ground motion. As it can be seen in Figure 14, the maximum compressive force in the deck decreases remarkably, and the distribution of axial force in the deck changes completely by using spatial cable system. Also, it is concluded from this Figure that the tension field at the middle of the main span, is eliminated by using spatial cable system. Figure 15 shows the average of maximum lateral deck displacements for all TTH excitations for bridge models in terms of main span length. It can be seen that increased lateral deck displacement is unavoidable in NLT model because of released lateral deck to pylon connection. However, in MXSC model, in spite of released lateral deck to pylon connection, the maximum lateral displacement decreased by almost 18%, compared to the NLT model. Figure 16 shows the average maximum longitudinal shear force and moment at pylon base, for all six records. As it is expected, the longitudinal responses decrease substantially when the spatial cable-systems are used in the cable-stayed bridges, in all range of span lengths. It is also observed that the MXSC system has better performance in transverse excitation, while the XSC system has better performance in reducing the longitudinal responses of the pylons. The spatial cable system reduces the longitudinal shear forces by approximately 36%, and longitudinal moment forces by almost 30%. Figure 17 displays the average of maximum lateral shear force at the pylons base, for all the 6 ground motions. Similar lateral deck to pylon connection causes the XSC and base models to demonstrate similar pylon lateral forces. It can be concluded that the XSC systems have no lateral influence with fixed deck to pylon connection, because of basic lateral mode shape of the deck, in which the main spatial cables are not engaged. As it was expected, the spatial cables in MXSC model work efficiently and reduce the lateral shear force in pylons by 21% especially in longer span [22- 28] (Figures 12-17).

An innovative supplementary spatial cross system arrangement of cables to mitigate the main seismic responses of cable-stayed bridges was introduced in this paper. Three-dimensional finite element models of cable-stayed bridges were constructed to investigate the seismic response of cable-stayed bridges with two different configurations of proposed spatial cable systems, different deck to pylon connections and three main span lengths. The models were analyzed under six earthquake excitations using nonlinear direct-integration time-history analyses. The following conclusions are made based on the finite element analyses results:

1. Supplying cable-stayed bridges with spatial cross system cable arrangement decreases the longitudinal seismic response of the deck as much as 47% for moment and 30% for shear force. It also has positive effect on reducing the lateral moment force in the deck by nearly 22%.

2. Releasing the transverse deck to pylon connection has major influence on decreasing the lateral shear forces in the deck and the pylons; although, it causes the maximum lateral deformation of the deck to be increased.

3. Using spatial cross-system arrangement leads to elimination of the tension field in the middle of main spans and reduces the maximum compressional force in the deck of cablestayed bridges.

4. Using spatial cross-system cables lowers the shear forces and moments in the pylons, especially in longer span cablestayed bridges.

None.

No conflict of interest.

1. Cámara Casado (2011) Seismic behaviour of cable-stayed bridges: design, analysis and seismic devices. Doctoral Thesis, ETSI Caminos, Canales y Puertos.
2. Wang PH, Yang CG (1996) Parametric studies on cable-stayed bridges. Computers and Structures 60(2): 243-260.
3. Maleki S, Maghsoudi Barmi A (2016) Effects of concurrent earthquake and temperature loadings on cable-stayed bridges. International Journal of Structural Stability and Dynamics 16(6): 1550020.
4. Allam SM, Datta TK (1999) Seismic behaviour of cable-stayed bridges under multi-component random ground motion. Engineering Structures 21(1): 62-74.
5. Dyke SJ, Caicedo JM, Turan G, Bergman LA, Hague S (2003) Phase I benchmark control problem for seismic response of cable-stayed bridges. Journal of Structural Engineering 129(7): 857-872.
6. Ren WX, Obata M (1999) Elastic-plastic seismic behavior of long span cable-stayed bridges. Journal of Bridge Engineering, 4(3): 194-203.
7. Ren WX, Peng XL (2005) Baseline finite element modeling of a large span cable-stayed bridge through field ambient vibration tests. Computers and structures 83(8,9): 536-550.
8. Karoumi R (1999) Response of cable-stayed bridges and suspension bridges to moving vehicles; Analysis methods and practical modeling techniques. PhD thesis, Kungliga Tekniska, Hogskolan, Sweden.
9. Kawashima K, Unjoh S (1991) Seismic behavior of cable-stayed bridges. In: Cable-stayed Bridges; Recent Developments and their Future. Elsevier science Ltd 193-212.
10. Fleming JF, Egeseli EA (1980) Dynamic behaviour of a cable‐stayed bridge. Earthquake Engineering and Structural Dynamics 8(1): 1-16.
11. Abdel Ghaffar M (1991) Cable-stayed bridges under seismic action In: Cable-stayed Bridges, Recent Developments and their Future. Elsevier Science Ltd 171-192.
12. Abdel Ghaffar M, MA Khalifa (1991) Importance of cable vibration in dynamics of cable-stayed bridges. Journal of Engineering Mechanics 117(11): 2571-2589.
13. Walker (2009) Modal superposition in the dynamic analysis of cable-stayed bridges. Master's thesis, Imperial College, London, UK.
14. Bruno D, Leonardi A (1997) Natural periods of long-span cable-stayed bridges. Journal of Bridge Engineering 2(3): 105-115.
15. He WL, Agrawal AK, Mahmoud K (2001) Control of seismically excited cable-stayed bridge using resetting semiactive stiffness dampers. Journal of Bridge Engineering 6(6): 376-384.
16. Fujino Y, Siringoringo DM (2006) Lesson learned from monitoring of long-span cable-supported bridges. Proc Third International Conference on Bridge Maintenance, Safety and Management, Porto, Portugal.
17. Liu W, Xu X, Wang R, Wang Z, Wu X (2006) Vibration reduction design of the Hangzhou Bay cable-stayed bridges. Structural Engineering and Mechanics 24(3): 339-354.
18. Morgenthal G (1999) Cable-stayed bridges; earthquake response and passive control. Master's thesis, Civil Engineering Department, Imperial College of Science, Technology and Medicine, London, UK.
19. Nazmy S, Abdel Ghaffar AM (1992) Effects of ground motion spatial variability on the response of cable‐stayed bridges. Earthquake Engineering and Structural Dynamics 21(1): 1-20.
20. Gimsing NJ (1983) Cable supported bridges: Concepts and design. J Wiley, Chichester, UK.
21. Pedro JJO, Reis AJ (2010) Nonlinear analysis of composite steel–concrete cable-stayed bridges. Engineering Structures 32(9): 2702-2716.
22. AASHTO (American Association of State Highway and Transportation Officials) (2010) AASHTO LRFD bridge design specification. Washington, USA.
23. Ali HM, Abdel Ghaffar AM (1995) Modeling the nonlinear seismic behavior of cable-stayed bridges with passive control bearings. Computers and Structures 54(3): 461-492.
24. ASCE (American Society of Civil Engineers) (2011) Minimum design loads for buildings and other structures. ASCE 7-10 Reston, United States.
25. Ye S Hu, Fan L (2002) Seismic Conceptual Design of a Three-tower Cable-stayed Bridge. Proc IABSE Symposium, International Association for Bridge and Structural Engineering, Zurich, Switzerland.
26. Wang R, Xu Y, Li J (2016) Transverse seismic behavior studies of a medium span cable-stayed bridge model with two concrete towers. Journal of Earthquake Engineering 21(1): 1-18.
27. Wilson JC, Gravelle W (1991) Modelling of a cable‐stayed bridge for dynamic analysis. Earthquake Engineering and Structural Dynamics 20(8): 707-721.
28. Wu W, Li L, Shao X (2016) Seismic assessment of medium-span concrete cable-stayed bridges using the component and system fragility functions. Journal of Bridge Engineering 21(6): 04016027.