Hydraulic Project Development and Corresponding Ecological Factor Analysis

Understanding fish swimming ability and energy cost could help for better design fish-friendliness hydraulic project. The fish swimming capacity is depends on a variety of factors such as the metabolic cost [1], oxygen requirement [2], turbulence in the water [3], types of muscles used [1] and fatigue times [4]. The fish swimming mechanism is also researched by many biologist, engineers and scientist [5]. For example, Heisey et al. [6,7] studies the survivability of fish passing through obstructs. Videler [8] and Webb [9] studied the relationship between fish swimming speed and the fish tail beat frequency and fish tail beat amplitude respectively. The length and speed of the body wave and body undulates are have infects on fish swimming [10-13]. The shape of the fish also has been considerable discussion in the literature, with various authors considering the fish shapes [14-18]. Modelling of swimming fish is a both river engineering and biological model system for understanding the mechanics activity during locomotion. In the last decade, a huge amount of efforts have been done by mathematicians to understand the dynamics of swimming in a fluid [19,20]. These models help to better understand the impressive swimming capabilities of fish. In order to gain insight into fishlocomotion, mathematic models are the desirable approach to use for testing fish locomotion to study fish swimming velocity, torques and energy cost during swimming. Experiments have shown that most fish swim using body undulations to generate thrust and maneuver in three dimensions [18]. So the patterns of body bending play a crucial role to understand their locomotion. According to Lauder et. al [18], the pattern of body bending during steady rectilinear locomotion has similar general characteristics in many fishes and involves a wave of increasing amplitude passing from the head region toward the tail. Real life fish are bodies of complexity shape and a complex surface roughness distribution due to the scales. For that reason, most researchers choose a prolate ellipsoid instead of fish. However, prolate ellipsoid could be faced with the huge error of biological criteria. Hence, in our research, we use the actual fish body shape instead of prolate ellipsoid to study the fish biological characteristics. To the best of authors’ knowledge, there are no published results on simulating the fish swimming ability and energy cost with the consideration of fish shapes, length and tail beat frequency. This paper a mathematic model is used to simulate the fish undulatory locomotion in the water. After a brief introduction of the theory of this model, we discuss the design of a robotic fish that allows measurement of self- propelled velocity, torques and the energy cost with two types of fish. We also address an important technical issue: to check the fish swimming ability in an ideal fluid. Our overall aim is to understand the swimming mechanics of different shape and different types of fish and calculate the energy of the fish expended which could be used as guidance criteria to design low fish mortality turbine and fish way.

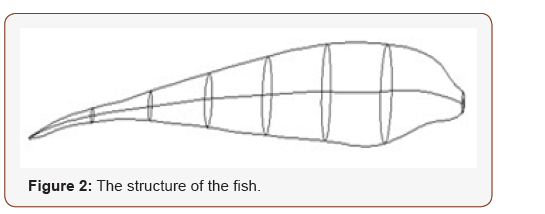
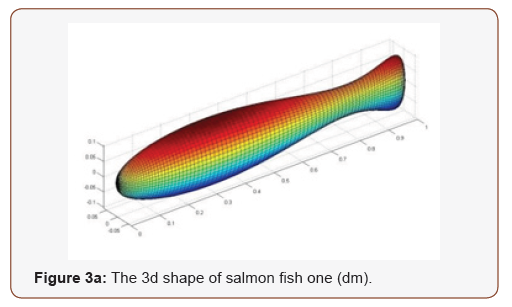
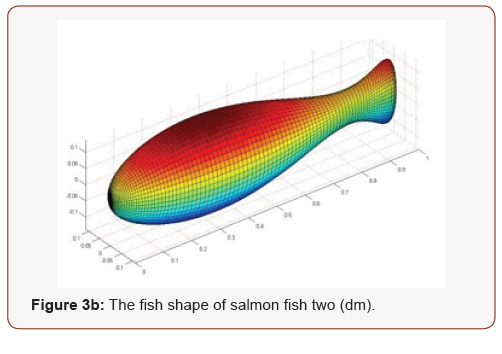
The constrain-based formulation for self-propulsion is described as follow. The fish is consisted by fish bone and the ellipse shape attached to the fish bone. The fish and its deformations are modelled according to a beam model. In other words, after the deformations of the fishbone are prescribed, each orthogonal ellipse of the fish is supposed to move rigidly, remaining orthogonal to the fishbone. Each ellipse shape is treated as a rigid body and the fish swimming paths are oriented by the first one. In the study, we assume the arc length of the fishbone to 1dm with 7 rigid bodies (Figure 2). In order to ensure the smooth of the fish, we need make the first and second derivatives for those parameters. When the second order discretization is made, the fish shape smoothly can be guaranteed (Figure 3A, 3B). After the salmon shape is defined, the sequential coupling of the salmon shape into the surface triangular mesh was done with accuracy of 10-3 and zero-gradient condition at the mesh on the computational domain is set. At every moment, the position and orientation of the fish are given by a pair (r, R) where r is a vector giving the position of the centre of mass of the fish and R is a rotation matrix giving its orientation. Every rigid fishbone (3D) has six degrees of freedom corresponding to its rigid component of motion and it is carried out in a frames(r, 𝜀) related to the fish. Where 𝜀 is the Euler angle (α, β, γ) of fish bone. We set the rotation angle (γ) of fish to 5 degrees which is to insure the stability of fish is during fish swimming [21]. The angle of α and β is change with time, in this simulation we define α and β are the tangent angle of 𝑠𝑖𝑛𝜃𝑡 in x and y axis. The fish tail beat frequency is also determined by sinusoidal motion. The first fish bone is defined by the real fish swimming path which is included in fish swimming control file (Figure 1). The fish swimming control file can be used to define the fish movement function. After get the hydrodynamics position of the first rigid bones of the fish, the following rigid bones can be defined through linear movement and rotation matrix.

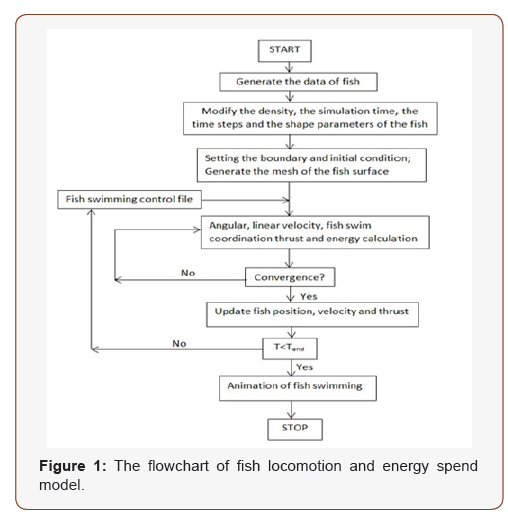
The total computational domain 𝜱, occupied by the fish is 𝜱B and the fluid domain 𝜱f=𝜱/ 𝜱B. Ω is the surface of the fish and n (Eq. 4) means the unitary normal vector to Ω directed toward the exterior of the fluid. The fluid is assumed to be irrotational, inviscid and incompressible and governed by Euler equations. The potential acting on the fish from flow is calculated by classical Kirchhoff’s equations. The forces and torques acting on the body are due to a combination of added-mass effects, skin friction and free vorticity [22]. These have been detailed described by Chambrion et al [23,24], Kanso et al [25], Munnier [20,26] and Kirchhoff’s equations has proved to be a very efficient for determining the hydrodynamic forces [27] and it has been a standard method when dealing with a problem of interactions between a perfect fluid and rigid immersed structures. The classical Kirchhoff’s equations are derived under the assumption that the rigid body is submerged in an infinitely large volume of an ideal fluid. Assume v and 𝜔 to be the linear and angular velocity vectors of the rigid body. The key issue in this model is to calculate the linear and angular velocity in fluid and through linear and angular velocity, the torques, the forces and the energy can be gotten. In order to calculate eulerian velocity exerted by the fluid on the fish’s surface, at every time step, the Laplace equation which is refer to as Kirchhoff’s equations set on 𝜱f will be solved according to the equations in fluid dynamics [24]. The overall potential is gotten as follow:

Where ω and υ are the angular and linear velocity vectors of the fish body, respectively; t is simulation time, σ is the density of the fish surface, x is the vertical distance between the surface mesh and the fish bones. I is the moment of inertia tensor, m is the fish body’s mass which is the integral of mesh; n is a unit normal to the surface of the body; p is a pressure at the fish body; T, Q and H are the Kinetic energy, hydrodynamic torque and force acting on the body, respectively. The integration is performed over the fluidexposed portion of the fish’s surface and the fish surface satisfies Neumann boundary condition. To solve the equations 1 to 5, the PDEs (governing the fluid flow) and the ODEs (driving the rigid motion of the immersed body) was used which are the toolboxes on Matlab [23,24]. In the algorithm above, the fish can be rigid and deforming, which is depends on the nature of the fish bending angles α, β, γ in the rotation matrix A and 𝑨−𝟏. Additionally, the fish is three-dimensional and it is an immersed surface and curve can be rigorously derived. The spatial order of accuracy will depend on the discretization of the spatial derivatives, and the interpolation scheme used in the Eulerian– Lagrangian coupling between the fluid mesh and the marker particles representing the solid body. The flow chart of our model is shown in Figure 1 (Figure 1).

Convergence criteria are based on the maximum errors in calculation. Convergence is ensured when the maximum errors become less than 10-9. The current numerical technique has been very successfully applied and validated in a series of recent papers [24]. Tests were conducted for the application to determine the dependency of solutions upon mesh size. Solutions were obtained with successive refinement of mesh size, i.e., reduction in mesh sizes. When solutions were observed to be unaffected by further refinements, they were presumed to be mesh independent.

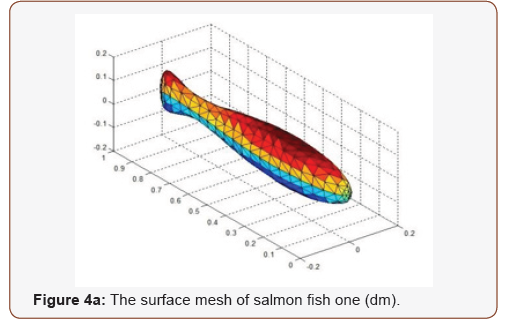
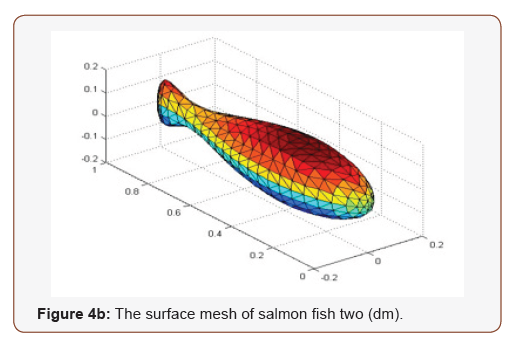
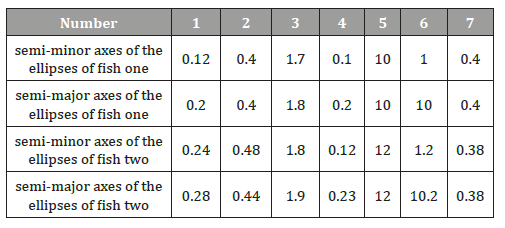
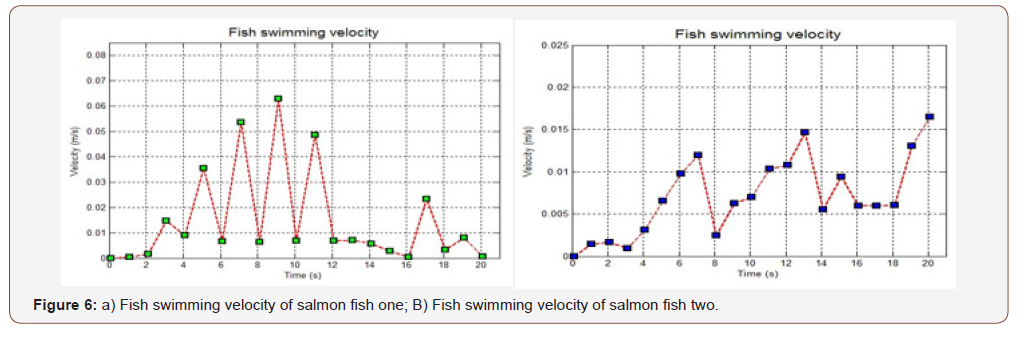
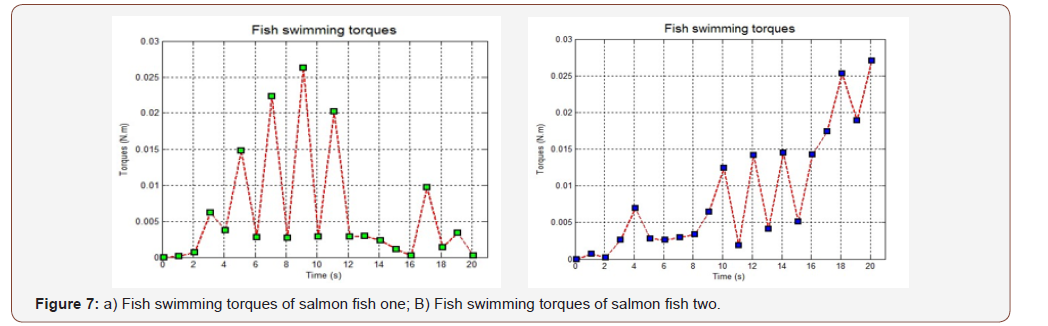
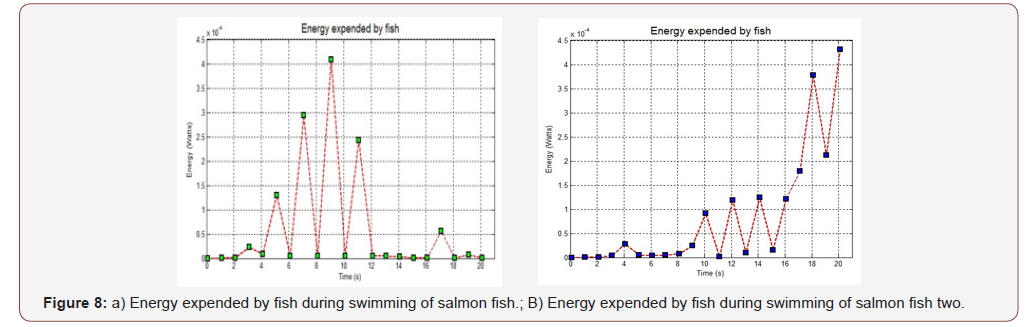
In this research we choose salmon as research object (Figure 4) to simulate. A general description of the fish calculation is presented as follow: First we set the parameters of the salmons (Table 1) and the shapes of salmons are described in Figure 2. The fish was discretized with a non-uniform mesh of 681 finite volumes (Figure 4).The trajectories of virtual fish were determined by the fish swimming control file (Figure 1). The fish swimming path was defined as moving on straight line in fluid. We get the velocity of the fish swimming (Figure 6), calculated the torques of the fish, and energy (T) of the fish during swimming (Figure 7). The simulation was carried out for a total time of 20 second. The time step was 0.01 s for most of this period. During the first second, a dynamic time step was used (starting with a step of 0.001 s) in order to achieve convergence at each time step during the initial fast transient period starting from the prescribed initial condition. All programs were implemented in Mat lab codes and simulations were run on AMD Athlon II PCs. Data analysis and visualization were done with Mat lab. Simulation time for a fish that of a fish with 681 finite volumes in 20 s, took approximately 1 hour (Table 1) (Figures 2-4).

Table: 1Fish shape parameters of salmon one and salmon two (mm).

In this section we validate the model by focus on two different shapes of fishes: I) salmon fish one, II) salmon fish two. These cases have been chosen to demonstrate the capability of our approach at fish swimming velocity, torques and energy expending simulation, to demonstrate easy application of the method to different fish, and to quantitatively compare the effect of shape and tail beat frequency on swimming performance of two fish.

The effect of shape on swimming performance

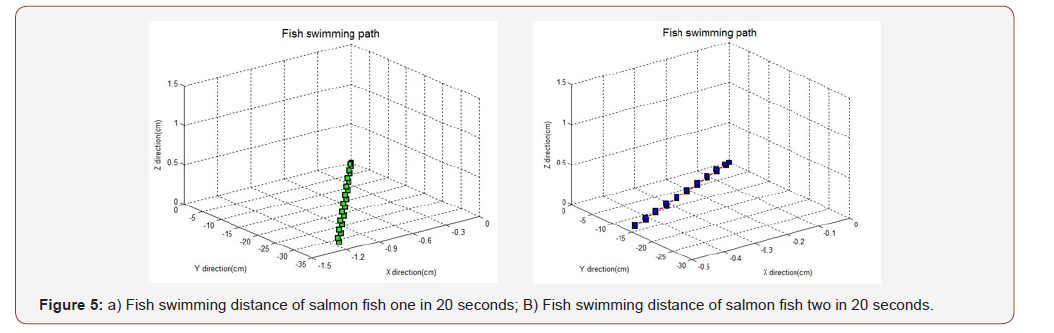
The two salmon shapes are indicated in Figure 2(b) and Figure 3 (b) and the comparison of salmon fish one and salmon fish two swimming distance is shown in Figure 5. The swimming distance, velocity, torques and energy expends of salmon fish one is represented by green grids, while salmon fish two is shown using blue grids to represent it. In order to ensure the consistency of the simulation, for the first and second fish, simulation time is set the same (20 s) and the tail beat frequency of two fish is also set the same (0.95 Hz). The velocity, torques and energy that fish spend during swimming are calculated and given in Figure 6, 7 and 8. The figure 8 is the animation image of the fish swimming. It is clear from the swimming distance shown in Figure 5(a) and Figure 5(b) that the first fish swimming distances is much bigger than the second one. The values of the swimming distance of fish one and fish two are 35.02 and 14.91 cm respectively. The average swimming velocity of fish one is also bigger than the fish two with 1.750 and 0.746 cm/s respectively. The energy expending of the two fishes are 1.49×10-4 and 1.73×10-4 watt respectively. A comparison of the effect of shapes on swimming performance are shown that the shape of fish have big influence in swimming ability which is similar to the conclusion of Reid [5]. Although the second fish spend more energy than the first one, but the velocity of the second fish are lower than the first one (Figures 5-9).

The effect of tail beat frequency on swimming performance

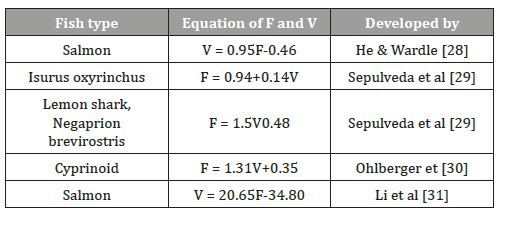
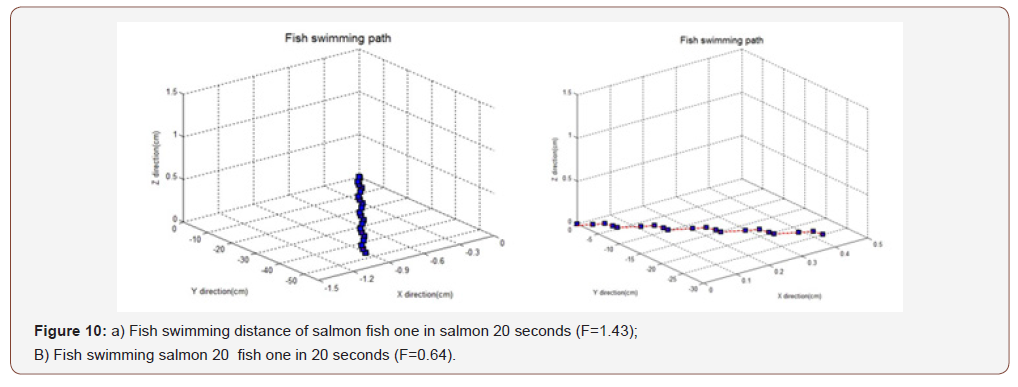
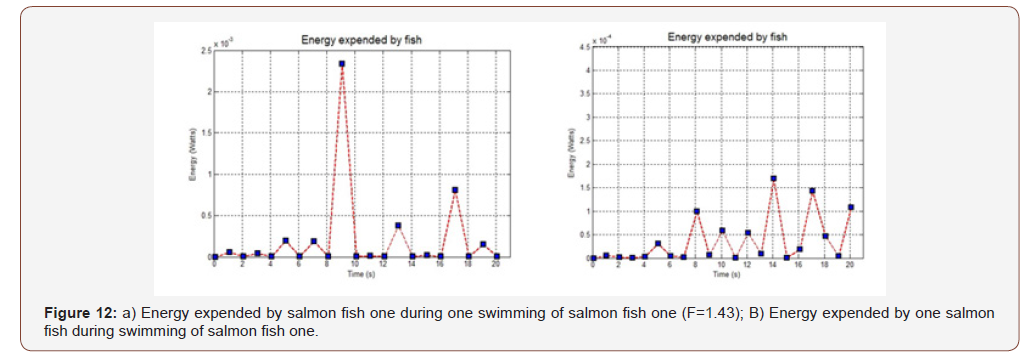
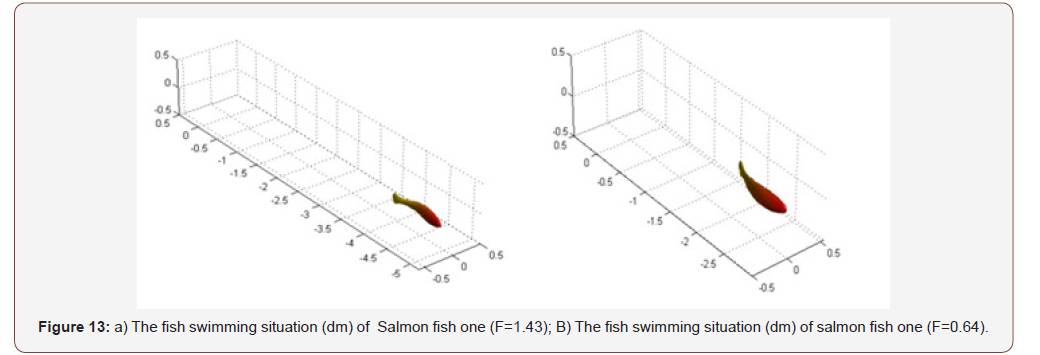
The tail beat frequency is often used for the analysis of swimming speed and many researchers have study the relationship between fish swimming and tail beat frequency (Table 2). Here, we use the same fish shapes with salmon fish one (Figure 2b) and same swimming time (20 s) with difference frequency to check the correlation between fish swimming velocity and tail beat frequency in our model. The tail beat frequency used in our simulation is defined as 1.43 and 0.64 Hz respectively. The swimming distance, the swimming velocity, the energy expending during swimming and the fish swimming images are shown in Figure 10, 11, 12 and 13. Figure 10 shows salmon fish one swimming distance for different tail beat frequency. From Figure 10 (a) and 10 (b), it is apparent that the fish with high frequency can swim longer than low frequency and the swim velocity are also increased with the beat frequency increase. The energy cost of the two fishes is also difference in two beat frequency types. The values of the swimming distance of fish one and fish two are 49.12 and 25.84 cm respectively. The value of the mean velocity of fish with high F and low F are 2.456 and 1.292 cm/s respectively. The energy expending of the two fishes are 1.49×10-4 and 0.61×10-4 watt respectively. This result has the same trend with empirical equation made by He et al [28], Sepulveda et al [29], Ohlberger et al [30] and Li et al [31]. Comparing the results of Table 2 and the results determined by our model, it appears that until both the fish shapes and swimming types are taken into consideration, the equation can be more accuracy. At this point, our model is more reasonable and described more specifically. Basically, even we don’t have the real fish data to evaluate our model, the agreement between the results in Table 2 and model calculation gives confidence to accept the model predictions. It is important that our model is matched to the actual situation of fish swimming, so that the fish swimming velocity and energy cost can be quantify with high accuracy (Table 2) (Figures 10-13).

Table: 2The relationship between fish swimming velocity (V) and tail beat frequency (F).

We presented a computational approach for fully resolved simulation of self-propulsion of 3d fish through an ideal fluid. This algorithm is developed that solves for the velocity of the fish for prescribed deformation kinematics. A solution for the fish swimming ability, turquoises spend during swimming and energy cost of the fish is also obtained. The effect of the shapes and the effects of fish beat frequency on swimming performance are also analysed. So the purpose of this model would be used to assist in the design of fish-friendliness of hydraulic structure, the resulting computer tool had to be very efficient and relatively easy to use. The fish design concepts provided here can be used for both reevaluating existing hydraulic structure as well as new structures design in order to improve their compliance with the new age of environmental awareness and fish safety. These concepts would also benefit the hydropower plant in many ways. We believe that understand the effects of fish shapes and tail beat frequency on fish swimming ability would result in a more efficient hydraulic operation and reduced operation and maintenance costs.

The authors thank Munnier, A. for his share the Matlab function codes of fish swimming and his invaluable contribution to this research and thanks CSC funding support (No.201163003). The fish swimming program codes used in this research work is the program developed by Fuenters M, Pincon B, and Munnier A and updated by Yao W the codes of fish swimming velocity, swimming torques energy expending and the swimming path are developed by Yao W.

No conflict of interest.

1. Bagur D (2009) Where the fish are: An Angler’s Guide to Fish Behavior, ISBN: 978-0-07-159292-5.
2. Enders EC, Herrmann J (2003) Energy costs of spontaneous activity in horse mackerel quantified by a computerized imaging analysis, Arch. Fish Mar Res 50: 205-219.
3. Liao JC (2007) A review of fish swimming mechanics and behavior in altered flows, Philosophical Transactions of the Royal Society, Biological Sciences 362 (1487): 1973-1993.
4. Nikora VI, Aberle J, Biggs BJ, Jowett IG, Sykes J (2003) Effects of fish size, time to fatigue and turbulence on swimming performance: a case study of Galaxias maculatus. Journal of Fish Biology 63(6): 1365-1382.
5. Reid DP (2011) Modeling the hydrodynamics of swimming fish, from individuals to infinite schools, PhD thesis, University of Groningen. ISBN: 978-90-367-5123-0.
6. Heisey PG, Mathur D, Euston ET (1995) Fish injury and mortality in spillage and turbine passages",proc. Intl. Conf. Hydropower, Waterpower 95, San Francisco, CA, USA.
7. Heisey PG, Mathur D, Euston ET (1996) Passing fish safety: a closer look at turbine vs. spillway survival. Hydro Review.
8. Videler JJ (1993) Fish swimming, Chapman and Hall, London, UK.
9. Webb PW (1971) The Swimming Energetics of Trout: II. Oxygen Consumption and Swimming Efficiency. Journal of Experimental Biology 55(2): 521-540.
10. Wardle CS, Videler JJ, Altringham JD (1995) Tuning in to fish swimming waves body form, swimming mode and muscle function. Journal of Experimental Biology 198: 1629-1636.
11. Tytell ED, Lauder GV (2004) The hydrodynamics of eel swimming, I. Wake structure, Journal of Experimental Biology 207: 1825-1841.
12. Müller UK, Smit J, Stamhuis EJ, Videler JJ (2001) How the body contributes to the wake in undulatory fish swimming: Flow fields of a swimming eel (Anguilla anguilla). Journal of Experimental Biology 204: 2751-2762.
13. Blake RW (2004) Fish functional design and swimming performance, Journal of fish biology 65: 1193-1222.
14. Affleck RJ (1950) some points in the function, development, and evolution of the tail in fishes. Proc Zool Soc Lond 120: 349-68.
15. Aleev YG (1969) Function and gross morphology in fish. Jerusalem: Keter Press.
16. Plaut I (2000) Effects of fin size on swimming performance, swimming behavior and roution activity of zebrafish Danio rerio. J Exp Biol 203: 813-820.
17. Wilga CD, Lauder GV (2004) Biomechanics of locomotion in sharks, rays and chimeras. In: Carrier JC, Musick JA, Heithaus MR (eds.) Biology of sharks and their relatives. Boca Raton: CRC Press.
18. Lauder GV, Lim J, Shelton R, Witt C, Anderson E, et al. (2011) Robotic Models for Studying Undulatory Locomotion in Fishes, Marine Technology Society Journal 45(4): 41-55.
19. Shirgaonkar AA, MacIver MA, Patankar NA (2009) A new mathematical formulation and fast algorithm for fully resolved simulation of self-propulsion. Journal of Computational Physics 228: 2366–2390.
20. Munnier A (2009) Locomotion of deformable bodies in an ideal fluid: Newtonian versus Lagrangian formalisms. J Nolinear Sci 19: 665-715.
21. Weihs D (1993) Stability of aquatic animal locomotion, Fluid Dynamics in Biology, 443-462.
22. Hown MS (1995) on the force and moment on a body in an incompressible fluid, with application to rigid bodies and bubbles at low and high Reynolds numbers. QJ Mech Appl Math 48: 401–426.
23. Chambrion T, Munnier A (2011) on the locomotion and control of a self-propelled shape-changing body in fluid. J. of Nonlinear Science.
24. Chambrion T, Munnier A (2012) Generic 3D swimmers in a perfect fluid are controllable, 2012 American Control Conference 4351-4356.
25. Kanso E, Marsden JE, Rowley CW, Melli Huber JB (2005) Locomotion of articulated bodies in a perfect fluid. J Nonlinear Sci 15(4): 255-289.
26. Munnier A (2008) on the self-displacement of deformable bodies in a potential fluid flow. Math Models Methods Appl Sci 18(11): 1945-1981.
27. Mougin M, Magnaudet J (2002) the generalized Kirchhoff equations and their application to the interaction between a rigid body and an arbitrary time-dependent viscous flow. International Journal of Multiphase Flow 28: 1837-1851.
28. He GP, Wardle CS (1989) Fish swimming behaviour research, Journal of Ocean University of Qingdao 19(2): 111-118.
29. Sepulveda CA，Graham JB，Bernal D (2007) Aerobic metabolic rates of swimming juvenile mako sharks, Isurus oxyrinchus. Mar Biol 152: 1087 -1094.
30. Ohlberger J, Staaks G, Hölker F (2007) Estimating the Active Metabolic Rate ( AMR) in Fish Based on Tail Beat Frequency ( TBF) and Body Mass. Journal of Experimental Zoology 307A: 296–300.
31. Li D, Lin X, Li X (2008) the influence of water flow on salmon behavior. Fishers 38 (6): 47-52.
32. Amaral SV, Hecker GE (2012) Designing leading edges of turbine blades to increase fish survival from blade strike, Conference on Environmentally - Enhanced Hydropower Turbines.
33. Michael E, Colgate JE, Maclver MA (2006) Generating Thrust with a Biologically-Inspired Robotic Ribbon Fin, Intelligent Robots and Systems, IEEE/RSJ International Conference.