Finding Optimal Routes for Main Haul Roads Development in Mountainous Open Pit using A* algorithm

Generally, the cost associated with hauling ore and waste to the concentrating mill or waste dump can vary greatly depending on the main haul road layout results [1]. Therefore, finding optimal routes for main haul roads development is very important for opening-up the mountainous open pit with complex relief. Though it is a complex problem to be considered the general elements for geometric design of main haul roads including road width, sight distances, maximum sustained gradient, vertical curve type, safety distance and haul road maintenance, etc. [2,3], but it is an essential task for finding optimal routes on truck haulage operation [4,5]. Actually, it may be said that route finding problems for main haul roads development in surface mine are referred to path planning (i.e. least cost path analysis: LCPA) using artificial intelligence algorithms in forest or city. In particular, many researchers have used Dijsktra algorithm (DA), A* algorithm and genetic algorithm (GA) for path planning problems [6-9]. A* algorithm is the most well-known path finding algorithm developed by Hart in [6]. The A* algorithm can be considered as the best first search algorithm that combines the advantages of uniform cost and greedy searches. Similarly, DA proposed by E.W. Dijkstra in 1959 is the way to find the path of minimum length between 2 nodes; it is still one of the well-known graph traversal algorithms. Rahman et al. [10] proved that A* algorithm is the best efficient method for route finding the shortest path and the least cost in respect of calculation time and CPU memory among them through comparison experiments using Breadth-first algorithm, A* algorithm and DA.

While Qu et al. [11] have clearly showed that neither the algorithm nor the common method can provide drivers with a satisfactory solution for wayfinding in a complex road network of the city on the basis of analysing the advantages and disadvantages of the shortest path algorithm and the problem solving based on knowledge method. Besides, Dong et al. [12] used an ant colony optimization method for fuzzy vehicle routing problem, and Abraham et al. [13] found the alternative routes in road networks with independent cost function. Also, Arunadevi et al. [14] selected route to a given destination on an actual map under a static environment, with a parallel genetic algorithm (PGA) implemented using high performance cluster. Besides, Hasmadi et al. [15] used GIS module with gradient, elevation and distance as elements in planning road in forest. Recently, some researchers presented the route-finding methods by combining path search algorithm mentioned above with GPS or geographic information systems (GIS) in order to determine the optimal routes of haul road in the open pit [16-18]. Particularly, Choi et al. [19] developed a new raster-based GIS model that combines multi-criteria evaluation and LCPA to determine the optimal haulage routes of dump trucks in large scale open pit. The model logic can consider multiple criteria simultaneously (i.e. speed, water body, ore body, curve, visibility, haul road maintenance) and can rate the adverse factor scores of truck movement using fuzzy membership functions.

Recently, some researchers have been studied the optimal path finding at the local scale such as path for mountain climbing [20] and a temporary haulage road interconnecting a mine [21] by using the raster based LCPA. Choi & Nieto [22] proposed a new LCPA algorithm to analyse the travel path that minimizes the movement time or fuel consumption of truck in open-pit mines. However, these studies mostly focused on the path planning problem using optimization techniques after haul road network have been already formed in research area. Especially, Baek & Choi [23] suggested a new method for haul road design in surface gold mine by using raster- based LCPA proposed by Choi & Nieto [22] to support efficient truck haulage operations. This method is appropriate for road layout optimization in open-pit mines or construction sites because it allows for consideration of the terrain slope and rotational angle of trucks. Here, the road layout was analysed through the LCPA using the mine design data and the zigzag-shaped road layout was simplified appropriately for the actual road design using Douglas-Peucker algorithm in condition of 2D instead of 3D. Finally, a 3D topographic model was produced by combining a 3D topographic model of the open pit mine including a bench design with a 2D road layout design result. The aim of this study is to demonstrate the capabilities of A* algorithm for finding optimal routes of main haul roads in open pit in condition of 3D and in the planning and designing stage of the surface mine that a main haul road does not exist. In this paper, therefore, we propose a new method to fine the route of main haul roads for opening-up the mountainous surface mine by digitizing the opening-up area in 3D environment and extracting the 3D coordinate values in the deposit zone using Geovia Surpac software (Version 6.6), and then searching an optimal route for main haul road using modified A* algorithm with new constrained conditions reflecting the gradient and the complex topographic relief. The applicability of the method proposed is verified by route finding of main haul roads for openingup a limestone mine, DPR of Korea.

A* Algorithm

LCPA is one of the spatial optimization techniques and is considered the most useful method for determining the optimal path from one or more origin nodes to one or more destination nodes. A* algorithm has all the advantages of the finding method such as DA, which is used in finding the best nodes and the LCPA. Therefore, at present, A* algorithm has been widely used in finding the optimum path in various fields [16,24,25]. A* algorithm uses a heuristic function to estimate cost from each node to the destination to guide path search. The cost associated with a node n is defined as follow:

C(n)=S(n)+D(n) (1)

where C(n) is the sum of route cost; S(n) is the actual cost of the path from the start to node n; D(n) is an estimated cost from node n to the target nodes.

During the search, A* algorithm maintains two lists of nodes, the open list contains the nodes that have to be considered next and the closed list contains the nodes already visited. The algorithm itself consists of expanding the one from the open list whose fitness function is minimal. Expanding a node means putting it into the closed list and inserts the neighbours into the open list and evaluating the fitness function. The algorithm stops when the goal of node is expanding. The function S is the cost from the start node to the finding node and D is the prediction cost from the exploring node to the target node. The cost C in the finding node is calculated in the sum of S and D. The path points are defined as the nodes which have a least-cost path compared with the costs of finding nodes.

The algorithm can be summarized as follows [6]:
Step 1. Define the start node and destination node.
Step 2. Load the map matrix.
Step 3. Add the start node to NEIGHBOURS list.
Step 4. Add the start node to CHECKED NODES list.
Step 5. Add the neighbour nodes to NEIGHBOURS list.

Calculate S, D and C cost function values. Record the parent to PARENTS matrix. Locate the C cost function value in the right place. If it is better than the old value, chance the parent with this parent in PARENTS matrix. Update S and C cost functions.
Step 6. If NEIGHBOURS is empty, no possible path Step 7. If the destination node is added to NEIGHBOURS, define the PATH using PARENTS matrix.
Step 8. Find the lowest cost node. Add it to CHECKED NODES and continue the finding on this node.
Step 9. Pull out the checked nodes from NEIGHBOURS. Go to Step 5.

Route finding method based on modified A* Algorithm

In this paper, the main parameters to determine the route for development road are defined as a longitudinal gradient of road, a road length and amount of construction work. The longitudinal gradient of road reflects the elevations of points and the stability of road, the road length – cost during operation and amount of construction work – the initial investment and therefore, they can be defined as the main parameters in building development roads. It is the most important to define the heuristic function in using A* algorithm. A* algorithm is to find a least-cost path, and the heuristic function is defined as the cost function. The cost function C is defined as the sum of the cost S of path from the start node to the present finding node and the prediction cost D from the present finding node to the target node. The cost S_i is calculated in the sum of haul cost and construction cost from the start node to the present finding node. When the start node is called “start”, the present finding node is called “i”, S_i is expressed as follows:

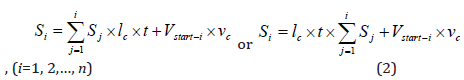
where S_i is the cost from start node to the present finding node; S_j is the distance between (j-1)^th node and jth node, m; lc is the operating cost unit of the main development roads, won/m∙year; t is the lifetime of the main development roads, year; V_start-i is an amount of construction work from the start node to the present finding node, m³; v_c is the cutting and filling cost unit, won/m³.

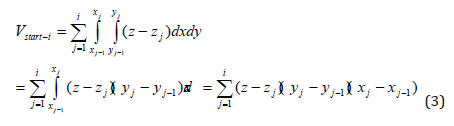
where z is the z coordinate value of area (x_j-1, y_j-1)-(x_j, y_j); i is number of the present node on the path list.

The predicting cost Di is calculated in the cost and from the present finding node to the target node. That is,

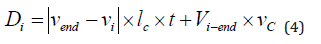
where v_i and v_end are the distance from start node to the present finding node and the target node, respectively; V_i-end is an amount of construction work from i^th node to the target node, m³.

The sum of cost in the present finding node from the above equation is calculated as follows:

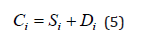
Also, in this paper, the constraint conditions which should be considered in searching the route of the main haul roads using A* algorithm are defined as follows;

Firstly, the gradient of the main haul roads should be less than the maximum longitudinal gradient and the code of gradient should be unchanged. It is related to be ensured the safety of haul work. Unchanged code of gradient means that if the gradient of road is started with positive code, it should be unchanged to the last, and if with negative code, it should be remained with “-” code to the last, because if the code of gradient is changed in the path, the haul distance can be longer.

Secondly, after the gradient interval, there should be sure the easement interval because the lifetime of engine may be reduced by overcoming the gradient interval. In other words, in order to ensure the safety of the main development roads, there should be the easement interval whenever it has either positive gradient or negative gradient.

Consequently, by combining the cost function of A* algorithm with the constraint conditions which should be considered in the path finding, we developed the modified A* algorithm to search the route of the main haul roads for developing surface mine with the serious topographic relief.

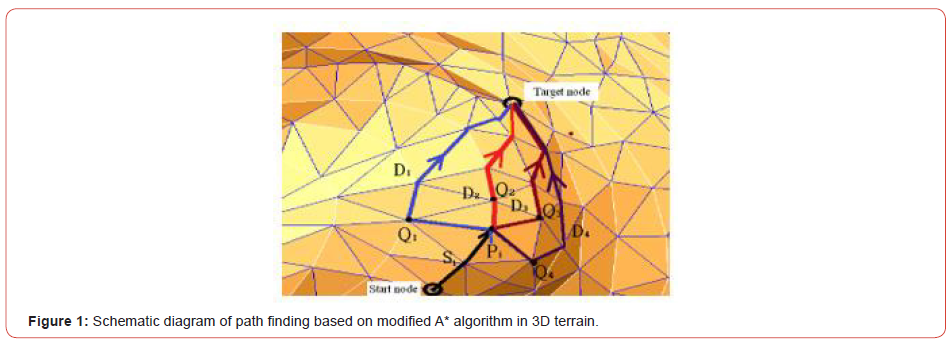
Based on the constraint conditions mentioned above, the schematic diagram of path finding by new A* algorithm is shown in Figure 1 as an example. Here, the optimal path is defined as the path D₂ through the point P_i and Q₂ (Figure 1).

The new algorithm in detailed is established as follows:

Step 1. Mine area terrain to be developed is digitized by Geovia Surpac 6.6 software.

The digitized terrain data are the *.str file with Surpac file format. x, y and z coordinate array of all the points on terrain of surface mine area to be developed is made by exporting *.str file data and it is used as the data field.

Step 2. Determine the two endpoints of the main haul roads to be constructed and input the x, y and z coordinates of two endpoints of the main development roads. The two endpoints of the main haul roads are determined around the open-pit mining field, overburden pile, crushing plant or explosive warehouse or on the already built road in the development area.
Step 3. Input the reference data for the design of the main development roads. In this stage, input the average and maximum value of longitudinal gradient of the main haul roads and the interval between terrain contours. And determine the theoretical length of the main haul roads using the average and maximum longitudinal gradient of the main development roads, the z coordinates of start node and target node.
Step 4. Search the path using A* algorithm. First, estimate whether the neighbour node of finding position is in the gradient interval or in the easement interval. If the node neighboured to the present finding point is in the easement interval, the next finding node is selected as node with the same z value until the length of easement interval according to the velocity of haul vehicles is satisfied. If the node neighboured to the present finding point is in the gradient interval, the next node is selected as node with the elevation according to the longitudinal gradient. And then, using above Equations. (2)-(5), calculate Si, Di and Ci of neighbour nodes satisfied judgment conditions of present finding node and select the lowest cost node among them and add it in the path node array, and search continuously.
Step 5. Finish the finding when the coordinate of target node is in the nodes array of path.
Step 6. Save the path.

Comparative estimation between modified A* algorithm and GA

In this study, we have compared A* algorithm with GA on the same opening-up project to analyse the advantages and disadvantages of proposed method. GA is stochastic search techniques inspired in the natural process evolution of species guided by the principle of the survival of the fittest. GA iteratively evolves a population of individuals representing candidate solutions of the optimization problem. The evolution process involves the probabilistic application of operators to find better solutions [14]. The solution of an optimization problem by GA starts with population random strings denoting several design vectors. The population size in GA is mutually fixed. Each string is evaluated to find its fitness values.

The population is operated by 3 operators: reproduction, crossover and mutation to produce a new population of points or design.

Reproduction is first operation applied to the population to select good string from pool. The reproduction operator is also called the selection “operator”. In a commonly used reproduction operator, a string is selected from the pool with probability proportional to its fitness. After reproduction, crossover is implemented to create new strings by exchanging information among strings of mating pool. Child fitness is higher than parents. The crossover is the main operator by which new string with better fitness values are created for new generation. So, we can say that reproduction operator selects good string for mating pool, the crossover operator recombines the substring of good strings of the mating pool to create string and mutation operator alters the string locally. The use of 3 operations successfully finds new generation.

Advantage of using GA is that it does not have much mathematical requirements about the optimization problems due to their evolutionary nature [24]. The evolution operators make GA effective at performing global search. GA for searching path of main haul roads in opening-up area of the surface mine is as follows.

Step 1. Prepare terrain data of ore deposit area.
Step 2. Input two endpoints of road.
Step 3. Consider a road route as an individual and input the number of individual and road route.
Step 4. Form a population of individuals by various routes between two endpoints.
Step 5. Evolve a population of individuals to 100 generations by reproduction, crossover and mutation.

At this time, reproduction probability is calculated according to fitness function f_k of the k^th individual as follows:

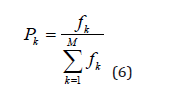
where P_k is reproduction probability of the k^th individual; M is the number of individuals in a population.
Fitness function f_k for selection is as follows:

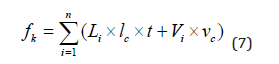
where L_i is the i^th interval length of road route, m; l_c is the operating cost unit of the main development roads, won/m∙year; t is the lifetime of the main development roads, year; V_i is an amount of construction work of i^th interval, m³; v_c is the constructing cost unit, won/ m³; n is the number of nodes in one road route. Fitness for finding optimal route is calculated as follows:

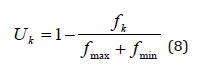
where U_k is fitness of the kth individual; fmax and fmin are the maximum and minimum value of fitness function, respectively.

Step 6. Calculate the fitness by Equation (8) and reproduce an individual that the fitness is higher and select an individual that the fitness is lower according to reproduction probability by Equation (6).
Step 7. Perform crossover with two individuals
Step 8. Mutate the string according to mutation probability.
The above operation is repeated until the stop criterion is satisfied as follows:

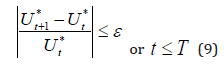
The individual corresponding to the maximum fitness given by the above operation is the optimal route of main development roads.

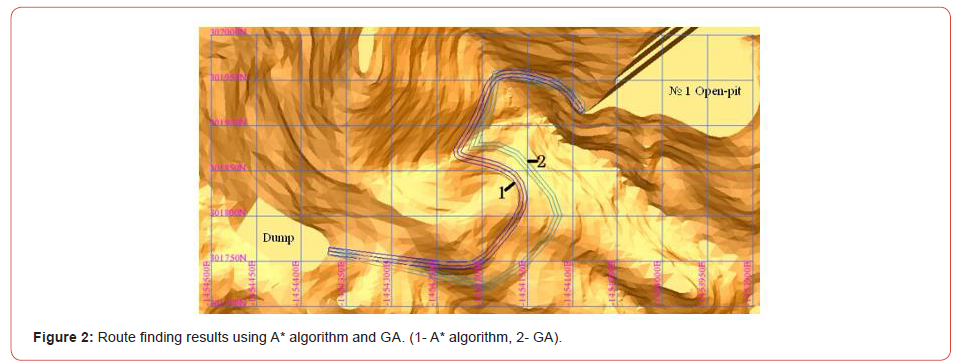
Figure 2 shows the results of route finding between № 1 openpit and dump by using GA and A* algorithm in conditions l_c=2 000 won/m∙year; t=5 year; v_c= 320 won/ m³, respectively. While Table 1 shows the coordinate values of searching nodes and route length and execution time by using two methods (Figure 2) (Table 1).

Table 1:Comparative estimation of route-finding results using A* algorithm and GA.

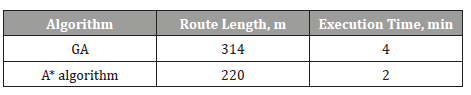
As shown in Figure 2 and Table 1 above, it can be found that route finding result using A* algorithm is better than GA, with shorter route length of 94 m.

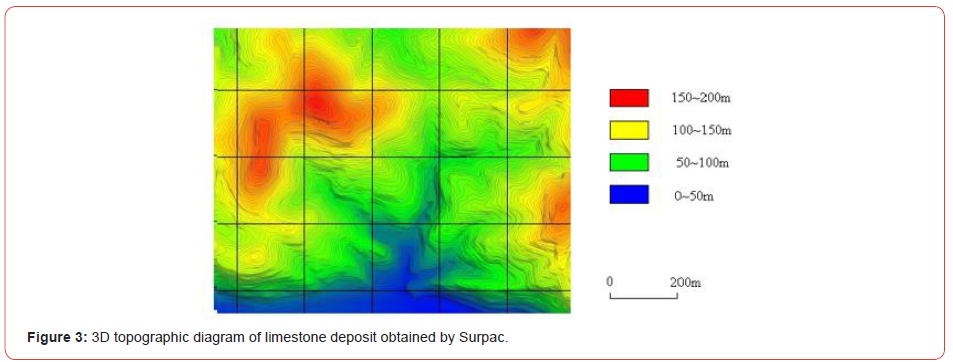
We have introduced the proposed method in development design of a limestone surface mine for Kangdong cement factory in Pyongyang, DPR of Korea. As the limestone deposit area is a mountainous deposit which the relief of terrain is heavy, it is located at 1°53′ E longitude and 39°6′ S latitude. The highest elevation in the study area is +155 m above sea level and the lowest elevation is +4 m above sea level.

Figure 3 shows the result digitized the mine terrain using Surpac. From Figure 3, we established the positions such as openpit, dump, explosive warehouse and crashing plant and so on and set up width, slope angle and gradient of main haul roads according to the characteristics of truck (Figure 3).

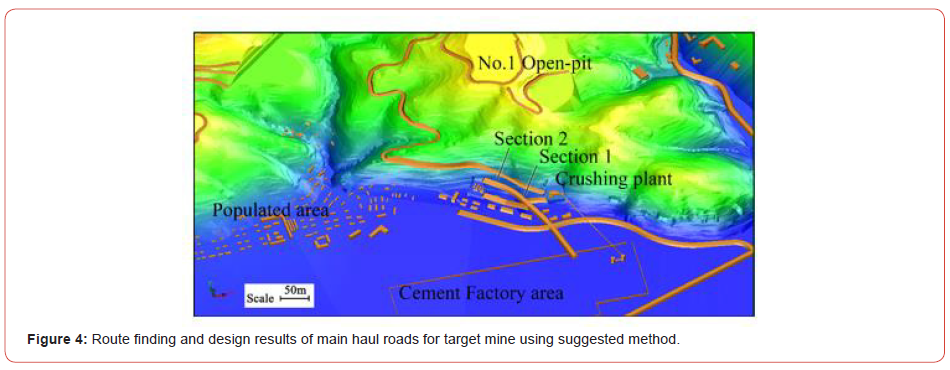
In case that 30 t trucks (average velocity 40 km/h) are used for haulage, width of main haul roads is 10 m and average and maximum longitudinal gradient is 6% and 10%, respectively. And length of slope interval is 150 m, length of easement interval is 60 m, curvature radius is 60 m in case that only one side gradient is applied in roads, is 100 m in case that two side gradient is applied in roads and minimum curvature length is 70 m. In addition, cutting slope angle is 65° and filling slope angle is 40° because the limestone deposit consists of hard rocks such as calcite and dolomite. In such conditions, we have searched the route of main haul roads for opening-up the limestone deposit in 3D condition using suggested method and designed the roads using Surpac in 3D environment. The final result is shown in Figure 4. In addition, the typical working drawings for haul roads are shown in Figure 5 (Figures 4,5).

In this study, we proposed a method to find the optimal route of main haul roads for opening–up the mountainous surface mine using A* algorithm in condition of 3D and to design main haul roads by using Surpac software in 3D environment. The proposed method can resolve the problems that occur when the route of main haul road is determined with the conventional LCPA method only. And this method enables us to find the optimal route of main haul roads for opening–up the mountainous surface mine in the planning and designing stage and in condition of which the main haul roads do not exist at all.

Conclusions obtained from research results above are as follows.
1. Firstly, the optimal route of main haul roads for opening-up the mountainous surface mine can be fully searched by combining the A* algorithm suggested in this paper and Surpac software.
2. Secondly, A* algorithm is more efficient than genetic algorithm (GA) in aspects to the least-cost and execution time for the optimal route finding of main haul roads.
3. Thirdly, this method can be applied to all kinds of the optimal path finding and road design for opening-up the mountainous surface mine.

In the real world, it may still be existed various types of obstruction factors such as hydrogeological condition, protection structures, and rock engineering conditions. Therefore, in future work, it would be interesting to improve the proposed method to consider the river, protection objects, rock condition and so on in finding the optimal route of main haul roads.

The data used to support the findings of this study are available from the corresponding author upon request.

The authors gratefully acknowledge the financial support from the National Science and Technical Development Foundation of DPR Korea (Grant No. 24) and the National Key Basic Research Program of DPR Korea (Grant No. 2019). The authors appreciate the help of many people on this project including the technical staff in Kangdong Cement Factory.

None.

1. Tannant DD, Regensburg B (2001) Guidelines for mine haul road design. School of Mining and Petroleum Engineering, Dept. of Civil and Environmental Engineering, University of Alberta, Canada pp.1-111.
2. Kaufman WW, Ault JC (1977) Design of Surface Mine Haulage Roads - A Manual. Design of Surface Mine Haulage Roads-A Manual; United States Bureau of Mines (USBM): United States Department of the Interior: Washington, DC, USA, pp.1-49.
3. Thompson RJ (2010) Mine Haul Road Design, Construction and Maintenance Management. Technical Report, Curtin University, Australia, pp.1-136.
4. Reis MS, Filho WLO, Oliveira E, Pena G (2014) Diagnosis about iron ore mine haul roads in the Quadrilátero Ferrífero-Itabira Complex case. REM: R. Esc. Minas, Ouro Preto, 67(4): 421-429.
5. Yadav PK, Singh RB, Kumar R, Singh RK, Ali M (2016) Design of Surface Mine Haul Road. International Journal of Science Technology & Engineering, 2(11): 228-233.
6. Hart PE, Nilsson NJ, Raphael B (1968) A formal basis for the heuristic determination of minimum cost paths. IEEE Trans Syst Sci Cybern 4(2): 100-107.
7. Anwar MA (2003) Integrating knowledge-base and Dijkstra's algorithm for finding best alternate route dynamically. 7th International Multi Topic Conference, 2003. INMIC 2003., Islamabad, Pakistan, pp.423-433.
8. Raichaudhuri A, Jain A (2010) Genetic Algorithm based Logistics Route Planning. International Journal of Innovation, Management and Technology, 1(2): 205-208.
9. Gupta DK, Jaiswal AK (2013) Path Planning with Real Time Obstacle Avoidance. International Journal of Computer Applications, 70(5): 15-21.
10. Rahman SMM, Ferdous AHMI, Nijami SH (2012) Comparative Study of Different Path Planning Algorithms: A Water based Rescue System. International Journal of Computer Applications, 39(5): 25-29.
11. Qu R, Weng M, Du QY, Cai ZL (2008) Combining Algorithm with Knowledge for Way-Finding. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, XXXVII (Part B2), pp.937-940.
12. Dong YW, Hao XY, Sato SY (2015) An Ant Colony Optimization Method for Fuzzy Vehicle Routing Problem. Innovation and Supply Chain Management, 9(1): 17–24.
13. Abraham, Delling D, Goldberg AV, Werneck RF (2014) Alternative Routes in Road Networks. Journal of Experimental Algorithmics, pp.1-12.
14. Arunadevi J, Johnsanjeevkumar A, Sujatha N (2008) Intelligent Transport Route Planning Using Parallel Genetic Algorithms and MPI in High Performance Computing Cluster. 15th International Conference on Advanced Computing and Communications, pp.579-583.
15. Hasmadi IM, Pakhriazad HZ, Mohamad FS (2010) Geographic Information System-Allocation Model for Forest Path: A Case Study in Ayer Hitam Forest Reserve. Malaysia, American Journal of Applied Sciences, 7(3): 376-380.
16. Kumar AJS, Arunadevi J, Mohan V (2009) Intelligent Transport Route Planning Using Genetic Algorithms in Path Computation Algorithms. European Journal of Scientific Research, 25(3): 463-468.
17. Greiner JR, Liu Y, Vyas BJ (2011) Systems and methods for designing a haul road. US Patent, 8078441 B2, filed Dec. 13.
18. Larbi EK, Boye CB, Peprah MS (2018) A GIS Approach in Optimal Route Selection in the Mining Communities Using the Analytical Hierarchy Process and the Least Cost Path Analysis. 5th UMaT Biennial International Mining and Mineral Conference, GLM, pp.50-62.
19. Choi YS, Park HD, Choon SW, Clarke KC (2009) Multi-criteria evaluation and least-cost path analysis for optimal haulage routing of dump trucks in large scale surface mines. International Journal of Geographical Information Science, 23(12): 1541–1567.
20. Rees WG (2004) Least-Cost paths in Mountainous Terrain. Comput Geosci 30(3): 203-209.
21. Alkinson DM, Deadman P, Dudycha D, Traynor S (2005) Multi-criteria evaluation and least-cost path analysis for an Arctic All-Weather Road. Appl Geogr 25(4): 287-307.
22. Choi Y, Nieto A (2011) Optimal Haulage Routing of Off-Road Dump Trucks in Construction and Mining Sites Using Google Earth and Modified Least-Cost Path Algorithm. Autom Constr.20(7): 982-992.
23. Baek J, Choi Y (2017) A New Method for Haul Road Design in Open-pit mines to Support Efficient Truck Haulage Operations. Appl. Sci. 7, 1-19.
24. Panich S (2010) The Shortest Path with Intelligent Algorithm. Journal of Mathematics and Statistics, 6(3): 276-278.
25. Vasishth O, Gigras Y (2014) Path Planning Problem. International Journal of Computer Applications, 104: 17-19.