 Research Article
Research Article
Evaluating the Effect of Support Rotation on the Buckling Modes and Critical Displacement of Elastomeric Base Isolators
Ehsan Kazeminezhad1*, Mohammad Taghi Kazemi2 and Seyed Mohammad Mirhosseini33
1,3Department of Civil Engineering, Arak Branch, Islamic Azad University, Arak, Iran
2Department of Civil Engineering, Sharif University of Technology, Iran
Ehsan Kazeminezhad, Department of Civil Engineering, Arak Branch, Islamic Azad University, Arak, Iran.
Received Date: December 20, 2019; Published Date: January 09, 2020
Abstract
Base isolation is one of the ways to stabilize structures against earthquake. In general, two types of system for isolate are used: laminated rubber bearing and lead rubber bearing. In this paper, the laminated rubber bearing is used. These isolators are made of bonded steel and rubber sheets with vulcanization. One of the most important factors for their design is stability because they can cause damage to the upper structures due to instability. For stability check the buckling load calculated based on the theory relation and compared with the finite element method. The support rotation causes a significant reduction in the buckling load and critical displacement of the isolators. In this research, the buckling load of square and circular isolator is calculated and shows that the buckling load of square isolator is higher than the circular ones and also rotation decreases the critical displacement.
Keywords: Laminated rubber bearing; Buckling load; Critical displacement; Circular bearing; Square bearing
Introduction
The most important concern of civil engineers in design is the acceleration and relative displacement of stories of building. To limit these items in structures, the dimension and construction costs will increase. Separating the earthquake vibration from the structure is one of the best possible methods. The separation method is performed by an elastomeric bearing. These supports cause the spectrum acceleration to decrease dramatically by increasing the natural period of structure and also cause the base shear to be reduced up to fifty percent. In conventional and mid-height buildings, the rotation does not occur at the joint between isolator and structures, but in high rise buildings and bridges that rotation can be observed. Rotation causes a changing in the buckling modes and the critical force. The laminated rubber bearing (LRB) consists of rubber and steel sheets. These bearings have low horizontal stiffness and high vertical stiffness. Staudacher et al. [1] reviewed the isolation history. The first idea for base isolation was introduced by Klantarintz in England showing that if a building is constructed on free lubricated seams and soft sand or mica, the seismic forces to the building will be reduced. It should also be said that the first base isolation device for a third-floor building was constructed in Yugoslavia. Tarics et al. [2] shown that the first rubber with relatively high damping was manufactured in 1984 at Malaysian Tire Manufactures Research Institute in England which was used in a US-based legal and judicial building. The shear stiffness of these rubbers is high in low strain, but when the strain increases that will decrease by 4 to 6 times and when the strain reaches at about fifty percent, that will reach to its minimum amount. The shear stiffness will also increase when the strain is a more than 100%. The building design with the base isolation theory was presented by Naeim & Kelly [3] revealing that the relative displacement decreases in the first and higher modes of vibration due to higher modes’ normal to the first mode and ground motion. Higher modes do not also have any effect on the building displacement. Ravi et al. [4] showed that for the combined compression and shear loading case the numerical prediction matches well with the experimental result. The comparison is particularly good in the shear strain range from 50% to 150% which is of actual interest in design. The variation in the vertical compressive load from 0 to 200% of the design vertical load does not influence the horizontal displacement response due to the shearing loading. Kelly (1997) developed a base isolation theory and provided the relationships for critical loading and created a new isolator calculation. Warn & Weisman [5] studied the coupled horizontal – vertical behavior of elastomeric and lead rubber seismic isolation bearing and also investigated the mechanical properties of isolators. Tsai & Hsueh [6] indicated that rubber properties depend on strain amplitude and the loading frequency. Thus, they employed the viscoelastic treatment to indicate the effect of damping on the bearing response. Karbakhsh et al. [7] point out that the nonzero initial boundary condition changes the mechanical properties of laminated rubber bearing and the ending rotation decreases the horizontal stiffness. Kelly & Takhirov [8] examined the tension buckling in elastomeric bearing and reported the upward displacement. They also presented a theoretical relation for the tension and compression buckling. This research is presented in three main sections. In the first part, we ensure the accuracy of the modeling in the software. In the second part, the effect of the rotation on the critical load is investigated and the third part effect of the rotation on the critical displacement is evaluated. The ABAQUS software was also used for the finite element method. The innovation of the work is that so far, the effect of the support rotation on buckling load and critical displacement has not been investigated and empirical relationships are only able to calculate buckling load in non-rotational conditions.
Assumptions and Methodology
Base isolator structure
Base isolator bearing consists of rubber and steel sheets. These isolators have high vertical stiffness and low horizontal stiffness to resist against the vertical load and lateral displacement respectively. Steel and rubber are connected to each other by vulcanization process. Two end plates (flanges) are also used in up and down isolators.
Isolator and material modeling
Two materials were used in the isolator bearing: steel and rubber. In the base isolator bearing steel is linear and rubber is highly nonlinear. Full 3D models in geometry and loading conditions for each isolator were used in this study. The hybrid C3D8H element and full integration C3D8 of ABAQUS have been used to model the rubber and steel shims respectively. To simulate the experimental conditions of applying the load, a dummy node at the top of the isolator is modeled. The node is connected with all the nodes lying in top of the end plate by multipoint constraints so that the end plate is constrained to translate in the horizontal direction as a whole. The vertical and horizontal forces were applied through this dummy node.
Rubber-like material in ABAQUS
For modeling rubber-like material properties, there exist many options such as hyperelastic and viscoelastic in ABAQUS. The hyperelastic behavior is used which is described as a function of strain energy potential defining the strain energy stored in the material per unit of reference volume (initial volume) as a function of strain at that point in the material. There are several forms of stain energy potentials available in ABAQUS to approximately model the elastomers: Arruda-Boyce, Marlow, Mooney-Rivilin, Neo-Hookean, Poly-nominal, Reduced polynomial, Yeoh and Van der waals. These were described in the ABAQUS documentation and were briefly explained here. Arruda-Boyce model is based on molecular chain network, it is also called Arruda-Boyce 8-chain model because it was developed based on the representative volume (hexahedron) element where 8 chains emanate from the center to the corners of the volume. This is a two-parameter shear model based only on I1 which works well with the limited test data. Arruda-Boyce model is shown in Eq.(1):
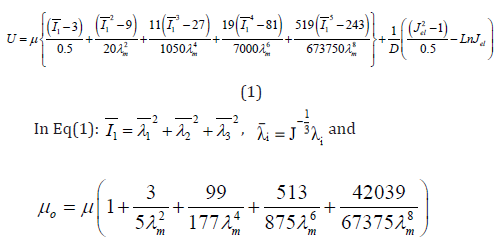
Mooney-Rivilin model has two phenomenological parameters which works well for moderately large stains in uniaxial elongation and shear deformation. Mooney-Rivilin model is shown in Eq.(2):
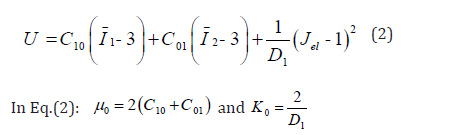
Neo-Hookean is a special case of Mooney-Rivilin form with C01= 0 and can be used when material data is insufficient. It is simple to use and can make good approximation at relatively small strains. Neo-Hookean model is shown in Eq.(3):
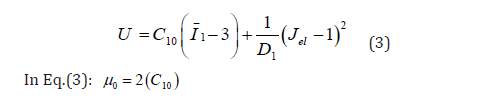
Ogden model is also a phenomenological model and is based on principal stretches instead of invariants. The model is able to capture the upturn (stiffening) of stress-strain curve and rubber models for large ranges of deformation accurately as well. Attention should be paid not to use this model with limited test (e.g. just uniaxial tension). A good agreement has been observed between Ogden model and experimental data for unfilled rubber for extensions up to 700%. Ogden model is shown in Eq.(4):
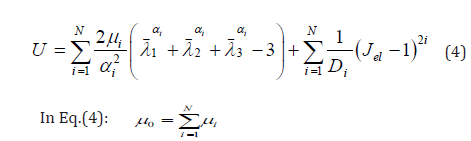
Polynomial model is used for isotropic and compressible rubber. This model is shown in Eq.(5):
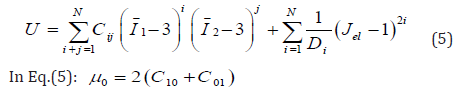
In Eq.(1) to Eq.(5), U; the strain energy per unit of initial volume, J el; elastic volume ratio, i ë ; principle stretches, μ; shear modulus, (λm, D), temperature rate depended material properties, I1, I2, I3 first, second and third deviatoric strain invariant, J, total volume ratio, K0 , initial bulk modulus and ì0 are initial shear modulus. Also C ij and αi are parameters corresponding to strain energy function to define ABAQUS material properties. In this paper, we used the experimental results of the rubber for extracting the energy function parameters. To do this, we have used the ABAQUS feature. Experimental results were achieved by Ravi et al [4] and Figure 1 to Figure 4 shows these (Figures 1-4).
The strain energy function parameters were gained by introducing Figure 1 to Figure 4 into the software and the curve fitting results (Figure 5 to Figure 8) indicated that there is good compliance between experimental results and ABAQUS output (Figures 5-8).

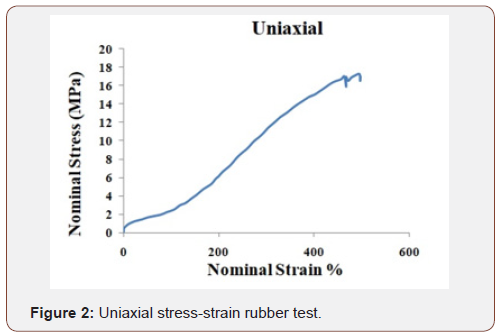
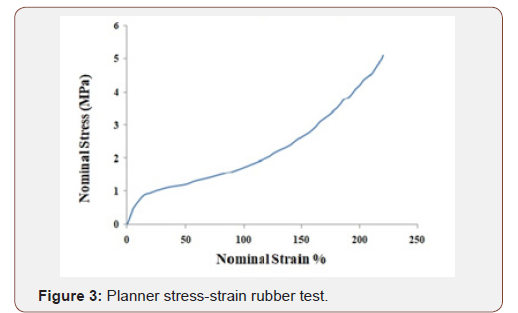
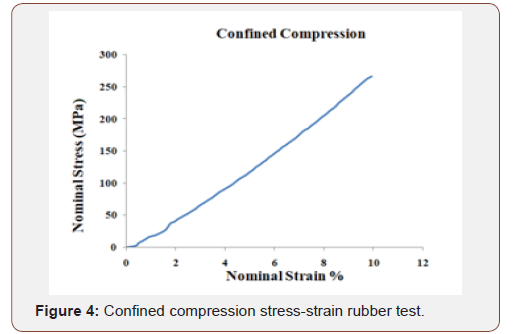
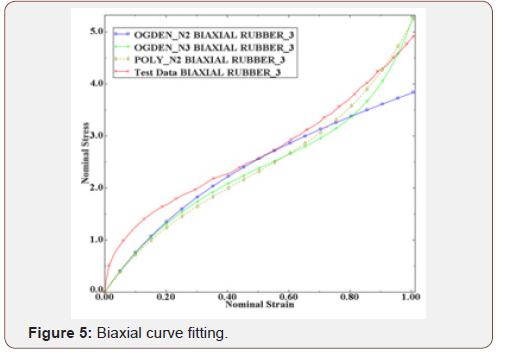
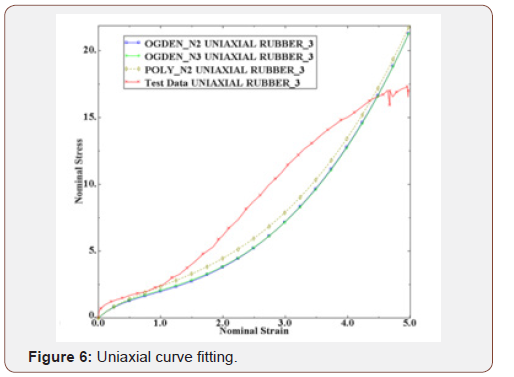
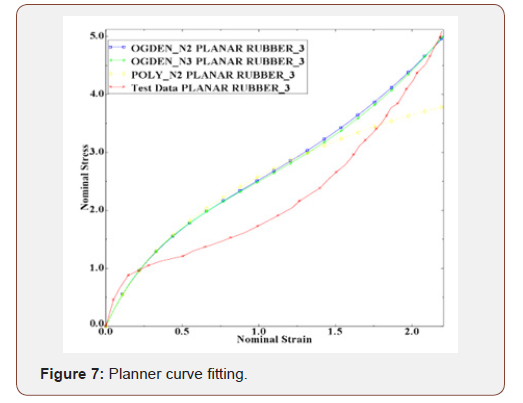

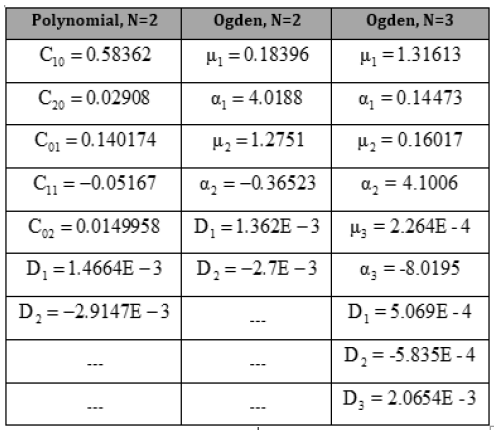
Table 1 shows the strain energy function parameters. These corresponding to second order polynomial and second and third order Ogden function. All dimensions are in Mpa as shown by Table1 (Table 1).
Table 1:
Part I
Verification
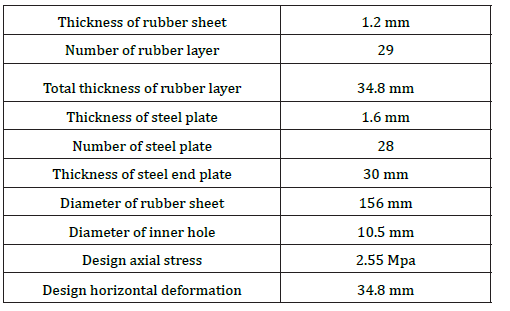
Geometry and properties of the verification model are shown in Table 2. This isolator based on the experimentally cyclic loading and Figure 11 shows the results (Table 2).
Table 2: Model verification properties.
Mesh modeling
Steel and rubber are divided into one and four layers in thickness direction. 8 elements in radial direction and in circumferential direction are divided into 24 parts (Figures 9,10).
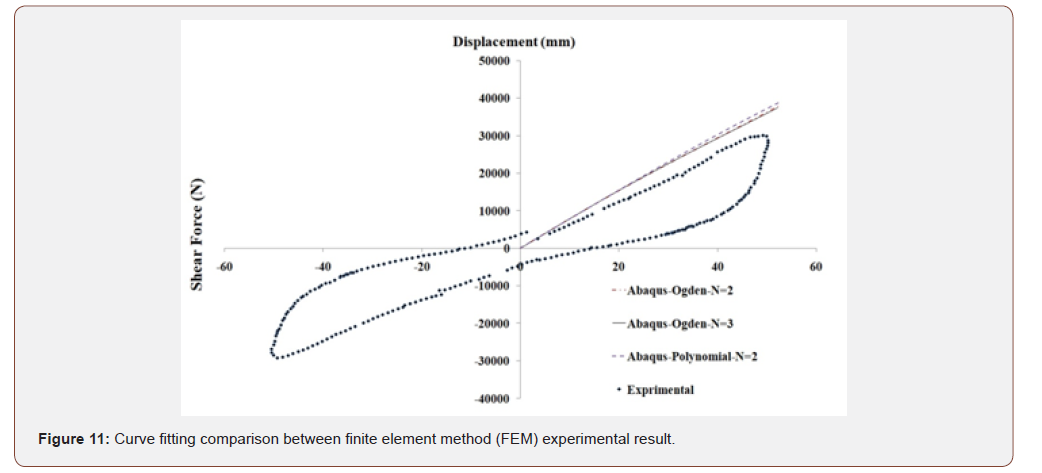
In this isolator C3D8 and C3D8H elements are used for steel and rubber respectively. Analysis was performed with 100% vertical load (48494 kN) and 150% shear strain equal to 52.2 mm horizontal displacement. (Shear strain is proportional maximum displacement to the total rubber height). There exists a fixed boundary condition at the end of each isolator and a horizontal and vertical displacement (U1 and U3 direction respectively) is allowed at the top of the isolator. Figure 11 shows the analysis result (Figure 11).
Figure 11 shows that FEM and experimental results are close together and also third order Ogden function is more accurate than the other functions.
Part II
The analytical solution of buckling behavior
The initial idea for the buckling elastomeric bearing was presented by Haring’s theory [9]. This is based on the column buckling theory to account for shear deformation. The external loading diagram of the elastomeric base isolators is shown in Figure 12 (Figure 12).
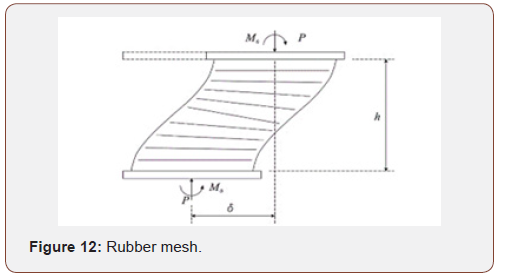

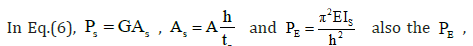 Pcr are Euler load of the standard column and the critical load of
elastomeric bearing respectively. As is the total cross-sectional
area; G, the initial shear modulus; A, the cross-sectional area; h, the
total thickness of elastomeric bearing without the end plates; r t the
total rubber thickness; EI s composite bending stiffness; θ0 bottom
rotation and θh top rotation.
Pcr are Euler load of the standard column and the critical load of
elastomeric bearing respectively. As is the total cross-sectional
area; G, the initial shear modulus; A, the cross-sectional area; h, the
total thickness of elastomeric bearing without the end plates; r t the
total rubber thickness; EI s composite bending stiffness; θ0 bottom
rotation and θh top rotation.
Model identification
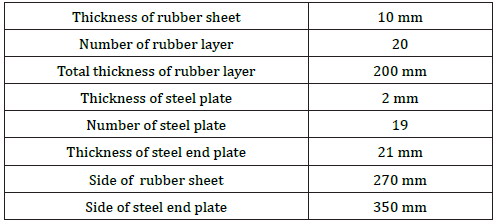
Two types of rubber material are used for circular and square isolators. The square isolator properties like area and thickness pads are same as the circular isolator. The geometry of circular and square isolator is shown below (Table 3 & 4).
Table 3: Circular geometry.
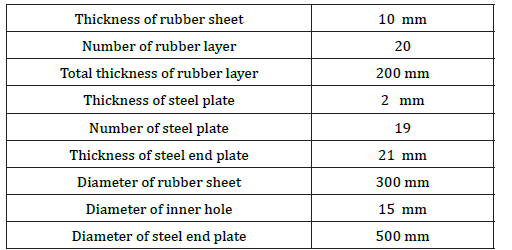
Table 4: Square geometry.
Material properties
Rubber materials are used in various types and wide range of shear modulus.
Table 5: Rubber shear modulus.
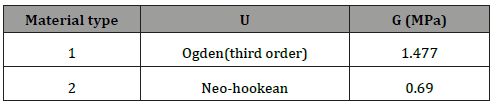
Type 1 rubber material is defined in Table 1 and Type 2 materials is defined in Table 6 with respect to the Neo-Hookean function.
Table 6: Rubber material.

Table 7: Steel properties.

Two kinds of boundary condition (B.C), which are different in rotation, are taken into account (Table 8).
Table 8: Boundary condition.

Two types of isolators, circular and square, with various boundary condition and rubber material were modeled and the buckling loading was calculated at each condition (Figures 13 & 14).
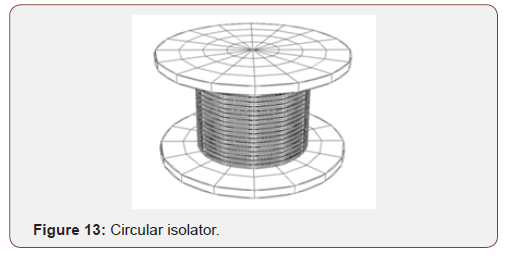
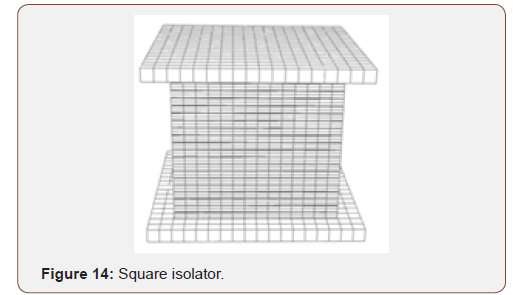
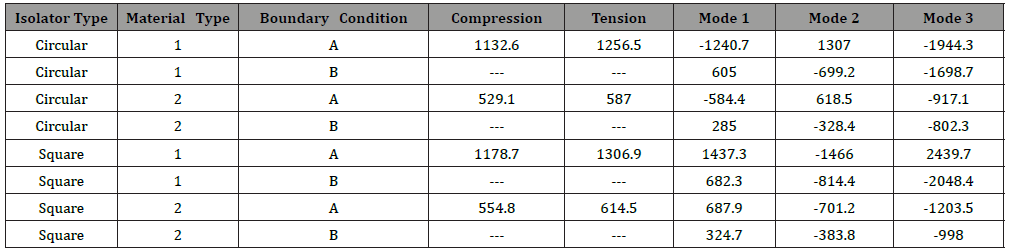
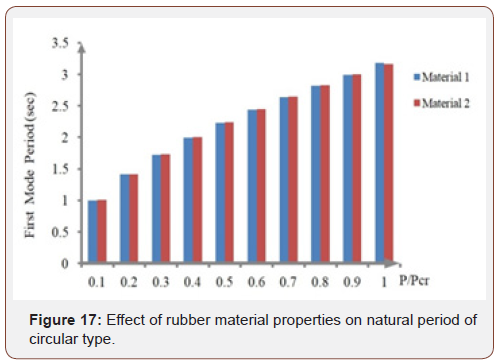
The finite element and analytical results are shown in Table 9. Based on the presented results in Table 9, the empirical and finite element result matched well. Also shows that the critical force decreased due to the top rotation of bearing. Also, the critical load is higher in square isolator than the circular isolator. As an example, first buckling mode shape of circular and square isolator in A boundary condition in Figure 15 and Figure 16 are shown. the effect of rubber material on the isolator period is investigated. The results show that the rubber material properties have not any effect on the natural period.
Table 9: Buckling load (kN).

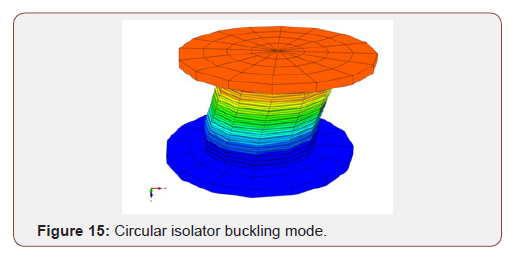
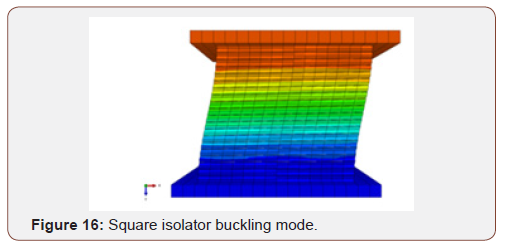
Part III
Effect of rotation on critical displacement
Weisman et al [5] were investigated the stability of elastomeric and lead rubber seismic isolation bearing. Sanchez et al [10] were assessment the static and dynamic stability of elastomeric bearing for seismic isolation. In this paper, we will first present the finite element model of the experimentally specimen and then, as a completion of their work, we will evaluate the effect of the rotation on the critical displacement values [13]. The scaled bearing is annular with an outer bonded rubber diameter of 152 mm and an inner diameter of 30 mm. The bearing consists of 20 rubber layers, each 3 mm thick; 19 steel shim plates, each 3-mm thick and two steel internal end plates, each 25-mm thickness. Based on Sanchez et al 2013, critical displacement is the point of the forcedisplacement curve that the slope of the graph reaches to zero. Based on the assumption Neo-Hookean model is used for rubber. Shear modulus of rubber 0.86 Mpa and Neo-Hookean parameters are C10 = 0.43Mpa , -1 1 D = 0.001Mpa . Steel elasticity modulus and poisons ratio are 200 Gpa and 0.3 respectively. Figure 18 shows the experimental results (Figure 18).
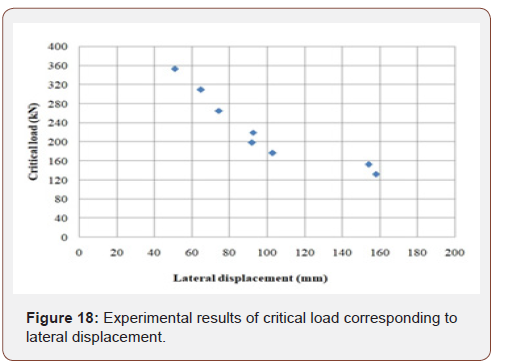
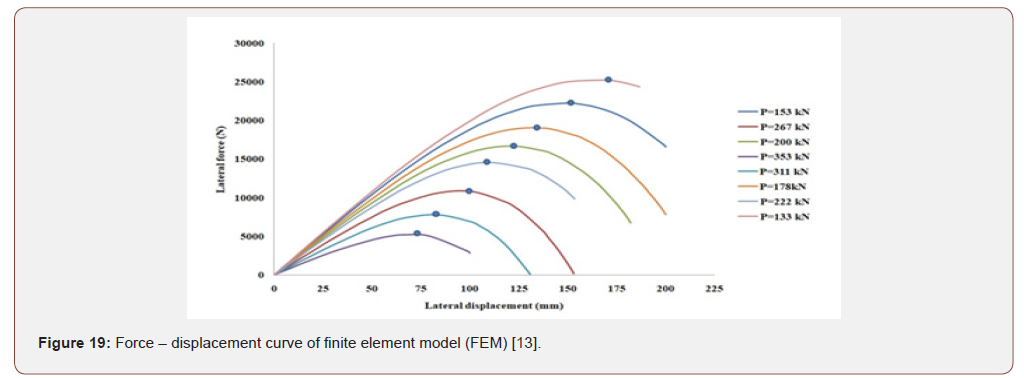

Force – displacement curve of finite element model (FEM) in various type of vertical load is shown and critical displacement location is displayed with a point. According to Figure 6, the boundary condition is such that the rotation at highest level of isolator is zero (θh=0) (Figure 19).
By changing the boundary conditions and creating a rotation of 0.1 radians ( θh=0.1), we repeat the procedure of calculating critical displacement and figure 20 shows the results(Figure 20).
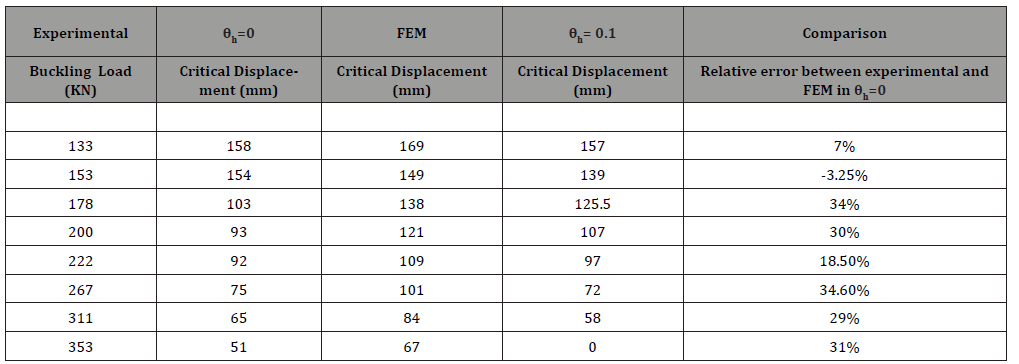
Table 10 shows the comparison between experimental and FEM analysis. As can be seen, the overlaps in force values 133 kN and 154 kN are good, but in other values of the force, the difference in results differs by up to 30%. Also, the 0.1 radian rotation caused a decrease in critical displacement (Table 10).
Table 10: Comparison of critical displacement between experimental and FEM analysis.
Conclusion
In this paper, in part II, two circular and square isolators with two types of rubber material were investigated and it was shown that the rubber material has a key role in the critical buckling force. Also, the boundary condition was investigated, and it was shown that rotation decreases the buckling force. The critical buckling load in square bearing was more than the circular bearing. Finally, the effect of rubber material on first natural period was evaluated and it was also shown that change in the rubber material does not have effects on the isolator natural period. The first mode period was calculated based on the mass ratio that is shown in Figure17. As can be seen from the results, it can be assured that the results of the finite element are acceptable and instead of spending a lot of time and cost using this method instead of the experimental method. It is also showed that the rotation reduces the critical displacement, and this state decreases the performance of isolator during an earthquake.
Acknowledgement
None.
Conflicts of Interest
No conflict of interest.
References
- Staudacher E, Habacher c, Siegenthaler R (1970) Erdbebensicherung in Baum. Zürich, Neue Zürcher Zeitung Tech.
- Tarics AG, Way D, Kelly JM (1984) The implementation of base isolation for the Foothill Communities Law and Justice Center Rep to Natl Sci Found Cty San Bernardino.
- Naeim F, Kelly JM (1999) Design of seismic isolated structures: from theory to practice. John Wiley & Sons.
- Ravi R, Selvaraj T, Chellapandi P, Chetal SC, Bhoje SB (1998) Finite element analysis of laminated rubber bearings-verification with KAERI HDRB, ALMR HDRB and CRIEPI LRB data. International Atomic Energy Agency, International Working Group on Fast Reactors, Vienna.
- Weisman J, Warn GP (2012) Stability of elastomeric and lead–rubber seismic isolation bearings. Journal of Structural Engineering 138(2).
- Tsai HC, Hsueh SJ (2001) Mechanical properties of isolation bearings identified by a viscoelastic model. International Journal of Solids and Structures, Elsevier 38(1): 53-74.
- Karbakhsh Ravari A, Bin Othman I, Binti Ibrahim Z, Ab-Malek K (2011) P-Δ and end rotation effects on the influence of mechanical properties of elastomeric isolation bearings. Journal of Structural Engineering, American Society of Civil Engineering.
- Kelly JM, Takhirov S (2007) Tension buckling in multilayer elastomeric isolation bearings. journal of Mechanics of Materials and Structures, Mathematical Sciences Publishers.
- Haringx JA (1948) On highly compressible helical springs and rubber rods and their application for vibration-free mountings I. Philips Res.
- Sanchez J, Masroor A, Mosqueda G, Ryan K (2013) Static and dynamic stability of elastomeric bearings for seismic protection of structures. Journal of structural engineering, american society of civil engineers 139(7).
- Hibbett, Karlsson, Sorensen (1988) ABAQUS/standard: User’s Manual, vol. 1. Hibbitt, Karlsson & Sorensen.
- Kelly JM (1997) Earthquake-Resistant Design with Rubber. Switzerland, Springer.
- Kazeminezhad E, Kazemi MT, Mirhosseini M (2019) Assessment of the vertical stiffness of elastomeric bearing due to displacement and rotation, International Journal of Non-Linear Mechanics.
-
Ehsan Kazeminezhad, Mohammad Taghi Kazemi, Seyed Mohammad Mirhosseini. Evaluating the Effect of Support Rotation on the Buckling Modes and Critical Displacement of Elastomeric Base Isolators. Cur Trends Civil & Struct Eng. 4(5): 2020. CTCSE.MS.ID.000598.
-
Laminated rubber bearing, buckling load, critical displacement, circular bearing, square bearing
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






