Study on Damage and Failure Mechanism of Steel Structure Affected by Temperature

The building structure is more and more complex, the number of floors is more and more high, and building structure fire is always a difficult problem to be solved. The change of the steel material properties at high temperatures leads to the reduction of structural carrying capacity, accelerates structural damage and building collapse, reduces the rescue time, increases the difficulty of rescue, and expands the fire hazard. For example, a fire broke out in hangar No.1 at Brunswick Naval Air Station in Maine, and the slab truss roof collapsed, destroying a large number of incoming aircraft [1]. A fire at an NT hangar at Prince George’s Airport in Canada has caused a light steel truss roof structure to collapse [1]. A welding fire terminal of Dusseldorf International Airport in Germany has caused a loss of 1 billion marks and killed 17 people [2]. A fire at an aircraft repair garage at Brussels International Airport has caused a massive collapse of a double-span prestressed continuous steel truss structure, costing billions of euros [3]. The roof of a light steel structure toy factory in Cihang Town, Sanxiang Town, Zhongshan City, Guangdong province, collapsed during the fire [4], the steel roof of the Dezhou department store in Shandong province collapsed in the fire [4], the dome of Jinan Olympic Sports Center collapsed after the fire broke out 4 hours [5]. A fire in the 24-story concrete Wealth Building in Wuxi City cost tens of millions of yuan and a fire in the north wing of the new concrete structure building of CCTV cost billions [6]. Therefore, it is clear that the material properties and structural change properties of steel, concrete, and steel-mixed composite structure under fire play a crucial role in the fire resistance of the structure.

In the past twenty years, the steel structure fire resistance can be divided into four analysis methods: test, component calculation, structure calculation, and fire randomness [7,8]. In 1991, the International Organization for Standardization gave the most widely used temperature curve ISO834 standard temperature curve [9]. In 1997, Dr. Ma proposed a simple calculation model for the heyday of fire through the analysis of several major international fire test data [10]. In 2000, the software developed by University of Liege in Belgium that can simulate and analyze two-dimensional and three-dimensional transient temperature fields [11]. The Dalian University of Technology has developed steel structure software which can calculate 2D and 3D temperature fields and internal force, deformation, and cracking of components [12]. In 2011, Dwaikat used load size and cross-section temperature gradient as the research breakthrough to investigate the buckling failure characteristics of single-side fire-exposed structures [13]. In 2011, Prof. Li studied the influence of the combined action of bending moment and axial force on the critical temperature of columns through load ratio, stiffness coefficient, slenderness ratio, and other factors, and proposed a calculation method for the critical temperature [14,15]. Chongqing University studied the strength and elastic modulus of Q460 high-strength steel at high temperatures and put forward the stress-strain relationship and the effect of the cooling method on the residual mechanical properties and the reduction coefficient [16,17]. In 2020, Jiang Yaqiang used the full-size portal rigid frame for a fire resistance performance test, and obtained the thermal response characteristics of the component and the temperature and displacement variation rules [18].

The microstructure evolution and fire prevention mechanism of micro-alloy anti-seismic fire steel plate after quenching were studied, the changes of the different microstructure of the plate during tempering and quenching were analyzed, and the mixed microstructure and fine compound carbide were obtained to make tempered steel have excellent fire resistance [19]. The experimental results of the mechanical properties of FRS under high temperature are introduced. The 99 tensile specimens of two different types of FRS and CSS steel structures were tested at room temperature and high temperature, and the stress-strain, mechanical properties, and deformation properties of the components under high temperature were analyzed. It is found that the FRS steel components have excellent fire resistance when the temperature exceeds 400℃, and the constitutive model of the strength and given the stiffness of the steel components [20]. The compression test of WGJ high-performance refractory steel welded steel column is introduced and established the finite element parameter analysis model. The experimental results are compared with those of China, Europe, and America. The results show that the Chinese, European, and American codes cannot be used directly to determine the buckling resistance of welded section columns with high-performance refractory steel. Then, proposed some suggestions for modification of the design method of the Chinese codes [21]. Six welded box sections with different width and thickness ratios were tested by section method, the magnitude and distribution characteristics of residual stress were obtained and analyzed, then the corresponding simplified residual stress model and the reason for the difference of residual stress were proposed [22]. The characteristics of fire load and failure mode of steel beam and column are discussed, the calculation method of joint stiffness after failure and the calculation mode of steel frame structure are given, and the most unfavorable method of calculating structure fire is put forward. Two calculation models of steel structure are used for verification [23]. The tensile test of domestic high-strength refractory steel with temperatures from 200℃ to 800℃ and natural cooling was carried out, and the stressstrain relationship curve and mechanical property parameters of domestic steel after high temperature cooling were compared with the properties of ordinary steel after firing at high temperature, and the variation coefficients of yield strength and tensile strength were fitted. The results show that the strength of domestic high-strength steel is slightly improved and the performance is stable after high temperature cooling [24]. The t distribution and confidence interval method in mathematical statistics are used to analyze the mechanical properties test data of high-strength steel at high temperature and after high temperature. The formula of mechanical properties index of high-strength steel at high temperature and after the high temperature is fitted. The strength transition temperature of high strength steel at high temperature is obtained, the strength reduction coefficient is lower than that of ordinary steel, and the elasticity modulus reduction coefficient at 600℃ is higher than that of ordinary steel [25].

In 2000, Silling proposed the basic idea of Peridynamics [26]. To make up for the deficiency of bond theory, the Peridynamics theory of ordinary state and non-ordinary state are proposed [27]. Kilic and Madenci use the method of overlapping common nodes to couple finite elements and PD [28]. In the steel structures, PD can show its characteristics perfectly by solving the problems of bilateral cracks, central double cracks, and oblique crack propagation [29-33]. Two- and three-dimensional crack simulation methods are proposed, and each method has its own unique advantages. For example, no additional unknowns need to be introduced to capture displacement discontinuity, suitable for large deformations and arbitrary nonlinear and rate-dependent materials, for modelling discrete cracks in meshfree methods and so on [34-38]. Demmie and Silling used the EMU code to calculate the damage and failure of mass concrete under blast load [39]. Bobaru used bond base Peridynamics to simulate the effects of stress waves and test geometry on the cracking of glass and high-intensity minerals [40]. To simulate the behavior of debris entering the atmosphere by using peridynamics, the temperature parameters of steel and aluminum alloy were calibrated by the tensile test. A calculation method for estimating PD damage parameters as a function of temperature was proposed and verified by experiments [41]. Utilized the Lagrangian formalism to derive the governing equations of Dual Horizon PD formulation which is for thermal diffusion analysis (Figures 1&2). From three different examples, these are a square plate with temperature and no flux boundary conditions, a square plate under thermal shock loading, and a square plate with insulation cracks, the good agreement is obtained between PD predictions and FEM results [42].

Under fire or high temperature conditions, indoor and component surface temperatures are constantly rising with time. The universally adopted temperature curve is the ISO834 standard temperature curve:

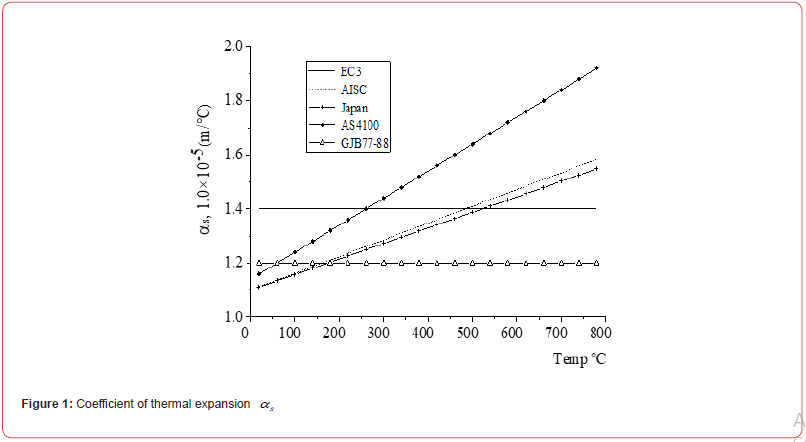
High temperature theory of steel structure The thermal expansion coefficient

The thermal expansion coefficient mainly affects the deformation and thermal expansion of steel structures. The calculation formula of the thermal expansion coefficient given by EUROCODE3

The exact calculation formula of thermal expansion coefficient given by AISC

The thermal expansion coefficient of steel proposed by Australian AS4100

The exact formula for calculating thermal expansion coefficient given by Japanese scholars

The thermal expansion coefficient of steel given by the code of steel structure

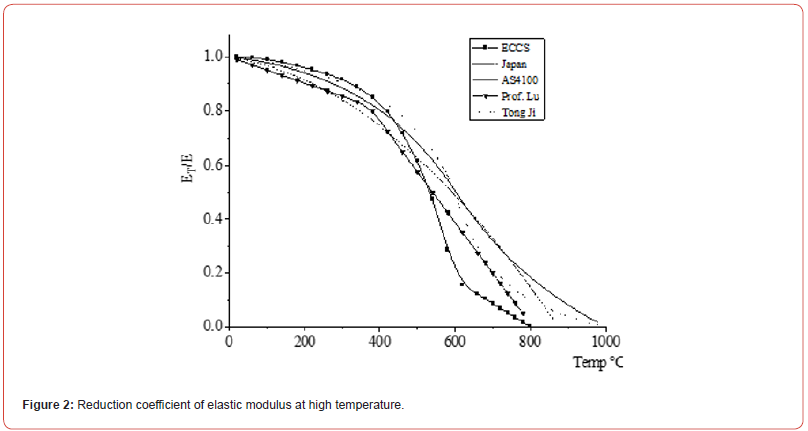
Reduction coefficient of elastic model

When the temperature rises to 300℃, the elastic modulus of steel begins to decrease obviously. When the temperature rises to 400℃, the elastic modulus decreases about 60%. When the temperature rises to 600℃, the steel loses its bearing capacity. The calculation method of elastic modulus reduction at high temperatures given by scholars of various countries as follows.

The calculation formula given by ECCS

in which, E is the elastic modulus of steel at room temperature, and E_T is the elastic model of steel at the temperature reaches T_s .

The formula of elastic modulus reduction coefficient given by Australian steel structure code

The calculation method of elastic modulus reduction coefficient given by Japanese scholars

The calculation method of elastic modulus reduction coefficient given by Tongji University

Density ρ_s

The density ρ_s of steel is relatively stable, basically does not change with the temperature change, and is considered to be fixed.

Poisson’s ratio s

The poisson’s ratio has the same property as density, which does not change with temperature.

Basic theory of Peridynamics

The traditional methods and means have many shortcomings in solving the problem of fracture and crack propagation. Fracture mechanics: stress singularity at crack tip; Finite element method: The crack is confined to the grid, and the crack propagation grid needs to be redivided. Extended FEM: The reinforced displacement field is not the true asymptotic displacement field near the crack tip, and the precision of the local displacement field is still not satisfactory. As shown in Figure 3, the Peridynamics discretized the object into many particles, and the integral method was adopted to overcome the shortcomings of previous methods. Combined with the interaction between particles, the scalar potential energy value w_(k)(j) is proposed. Combined with the interaction between the particle x_(k) and other particles in the range of action,w_(k)(j) ≠ w_(j)(k) , and the expression of the micro-potential energy is obtained

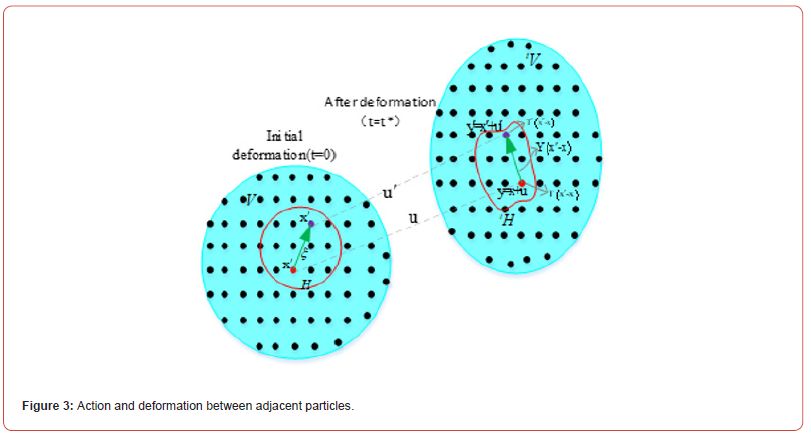
The strain energy density W_(k) of particle x_(k) is obtained by summing the particle x_(k) with the micro-potential energy w_(k)(j) of other particles in the range of action

The Peridynamics at particle x_(k) can be obtained by the principle of virtual work.

in which,T is the sum of the kinetic energy of the object, and U is the sum of the potential energy of the object,

Then the Lagrange equation at particle x_(k) can be expressed as

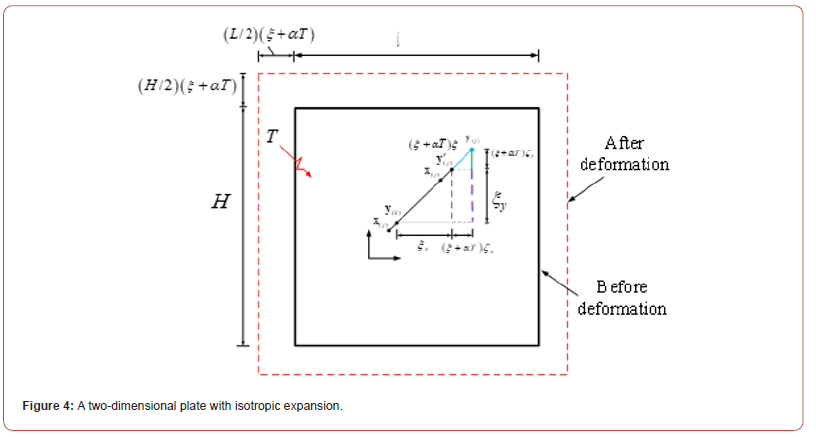
For two-dimensional positive strain ζ and constant temperature load T , as shown in Figure 4, the stress (k ) ó and strain (k ) å of the object can be expressed as

Two-dimensional material attribute matrix C can be expressed as

Where, the relationship between the volume modulus κ and the shear modulus μ and the elastic modulus E and Poisson’s ratio ν is

The expansion term θ_(k) and strain energy density W_(k) of two-dimensional expanding objects are expressed as

For two-dimensional expansion terms, the expansion θ_(k) of Peridynamics object and the strain energy density W_(k) are expressed as

Based on the classical continuum mechanics and Peridynamics, the expansion term θ_(k) is consistent with the strain energy density W_(k) for each expansion of two-dimensional object, and the Peridynamics parameters are as follows:

For the two-dimensional pure shear problem, as shown in Figure 5, classical continuum mechanics can be expressed as

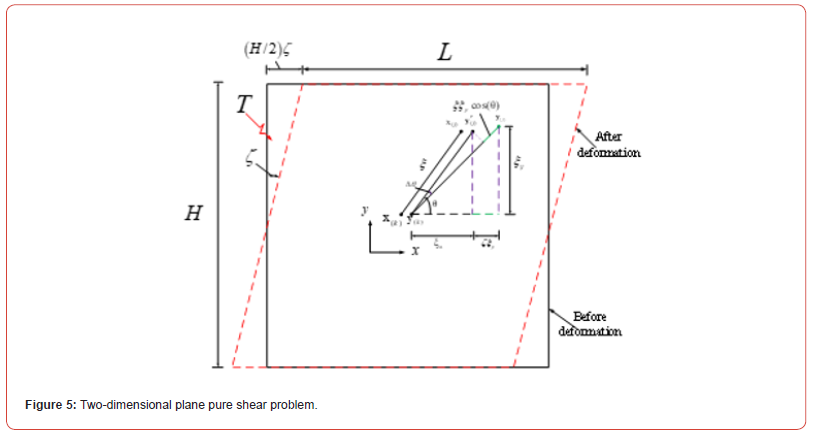
The two-dimensional Peridynamics strain energy density in pure shear state is

The strain energy density obtained by classical continuum mechanics and Peridynamics of various expansive two-dimensional objects under pure shear conditions is consistent, and the two-dimensional Peridynamics parameters can be obtained as follows:

By introducing the classical continuum mechanicsκ , μ and the material parameters of steel structure varying with temperature into the Peridynamics, the constitutive equation parameters related to the volume modulus and shear modulus of variable temperature Peridynamics are obtained.

Q345 steel plate was used to make the test with elastic modulus E = 203GPa , Poisson’s ratio ν = 0.3 , ultimate strength 572MPa σ_s = , elongation δ = 27.96% and density ρ = 7850kg/m3 at room temperature. The material properties at high temperature are calculated using formula (14) and Formula (15) of the calculation scheme given by Tongji University.

Crack propagation path under temperature

Q345 steel was used to make bilateral crack tests. The test numbers and crack sizes were shown in Table 1 & Figure 6. During the experiment, the load at both ends of the test is 2.217×10−5m/s displacement, and the test fracture results are shown in Figure 7. The results show that the longitudinal crack spacing has a great influence on crack propagation at normal temperatures. Under load, the test with a longitudinal crack spacing of 0mm expanded along a straight line and finally formed a horizontal crack, as shown in Figure 7(a). Under the load, the test with a longitudinal crack spacing of 10mm, first the cracks expanded along a straight line,when the longitudinal distance and horizontal distance of the crack tip were the same, the two cracks expanded along the 45°direction and finally formed an oblique crack, as shown in Figure 7(b). Under the load of the test with a longitudinal crack spacing of 20mm, the two cracks spread without affecting each other and finally formed two parallel oblique cracks, as shown in Figure 7(c).

Table 1:Bilateral crack test.

Three kinds of Q345 steel tests with different longitudinal spacing were established by PD. To understand the damage and failure law of the tests under the action of temperature, 150KN tensile load was applied to both ends of the tests to simulate the crack propagation results of the three tests. Figure 8 shows the final damage and crack growth path of the 200x tests under different temperatures and force loads. Under the action of temperature, the test with a longitudinal spacing of 0mm eventually forms a horizontal crack. However, with the temperature increasing, the elastic modulus of the test decreases, and the upper and lower edges of the base metal where the two horizontal cracks fuse appear a damaging trend, and the damaged area and damage value expand with the temperature increasing, which can be obtained from Figure 8(a) to Figure 8(d). Figure 9 shows the damage and crack propagation paths of test 2010x under different temperatures and force loads. Under normal temperature and load, as shown in Figure 9(a), the two cracks first expanded horizontally. When the longitudinal spacing and horizontal spacing of the two cracks were the same, the crack tip extended across the test in the direction of 45°. From Figure 9(b)-9(d), it can be seen that as the temperature increasing, the horizontal propagation distance of the two cracks decreases continuously. When the temperature reaches at 600℃, the two crack tips extend directly toward each other, forming an oblique crack, and local damage occurs in the fusion area of the two crack tips.

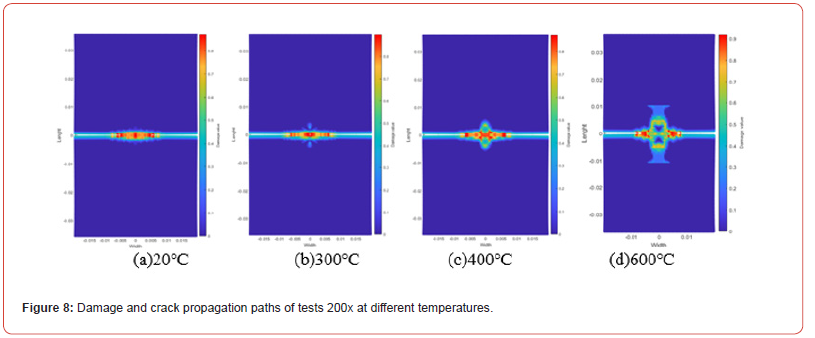
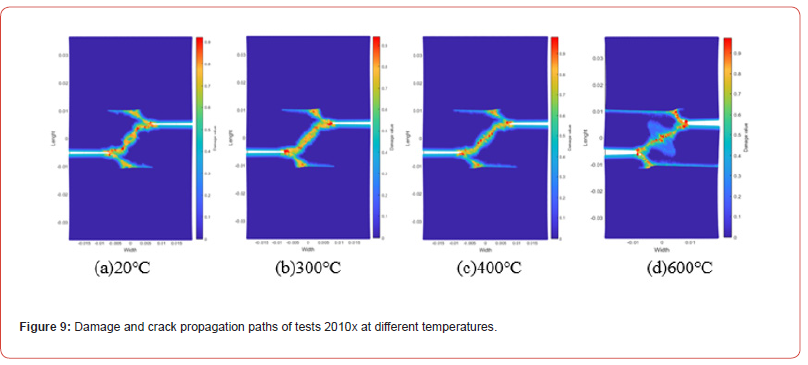
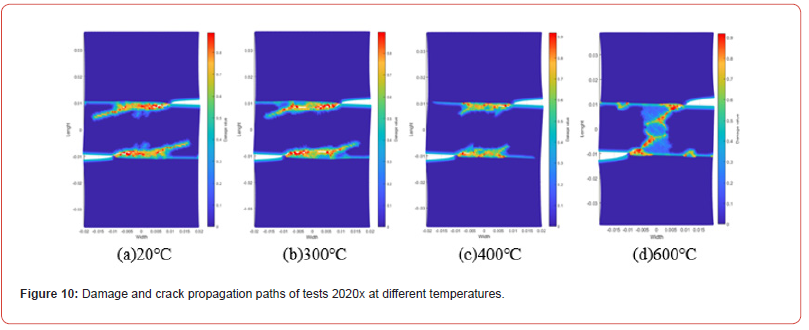
Figure 10 shows the damage and crack propagation paths of test 2020X under different temperatures and force loads. As can be seen from Figure 10(a), bilateral cracks spread along the horizontal direction at room temperature, forming two parallel cracks through the test. As the temperature increases, it can be seen from Figure 10(b) to Figure 10(d) that the horizontal propagation path of the double crack becomes shorter and the vertical propagation trend becomes obvious. When the temperature reached at 600℃, the tips of the two cracks almost extend towards each other, and the damage in the longitudinal spacing area of the crack is obvious and a crack formed.

Comparison of damage values of tests under temperature

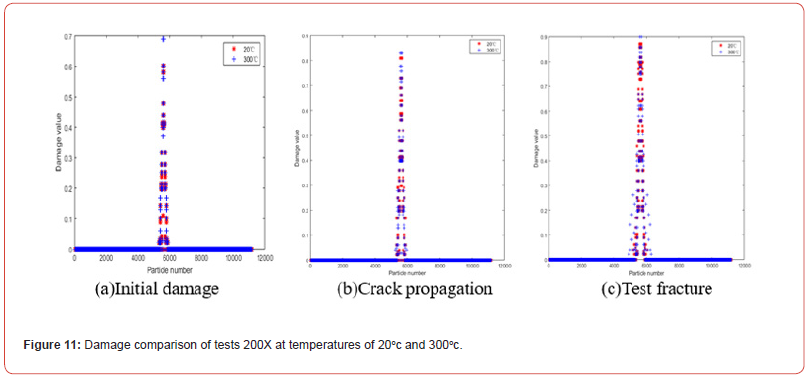
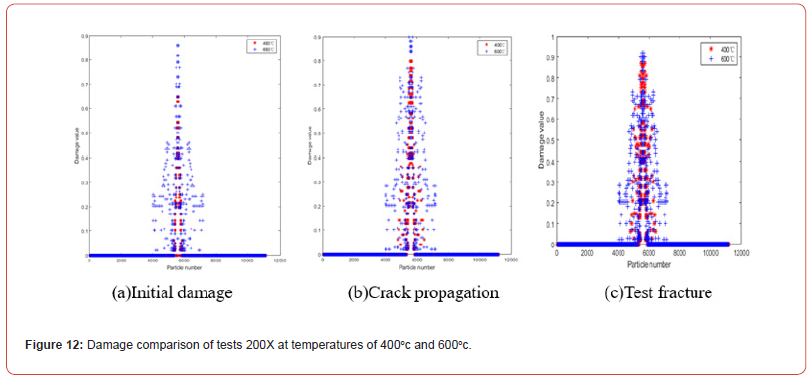
Figures 11 & 12 show the damage comparison of tests at different temperatures at 200X. It can be seen from Figure 11(a) and Figure 12(a) that at the initial damage stage, the damage rate of tests at high temperatures is faster and the damage value is larger than that at low temperatures. With the application of load, cracks spread and the difference in damage value caused by temperature difference gradually decreases. When the test breaks, the maximum value of the damage is almost the same at different temperatures. As can be seen from Figure 11, when the temperature is lower than 300℃, the damaged location of the test is almost located in the middle area of the test. When the test breaks, the damaged location of the test slightly diffuses from the middle to other locations of the test. As the temperature increases, as shown in Figure 12, the damage location of the test expands from the center of the test to the surrounding area. The higher the temperature, the larger the expansion range, which is consistent with the crack width path of the test in Figure 8.

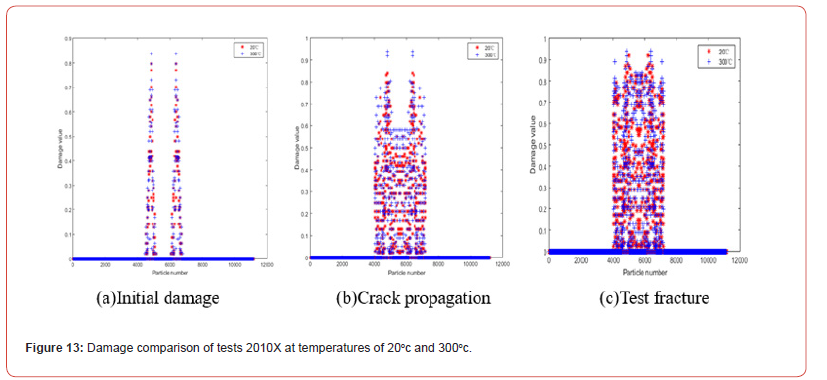
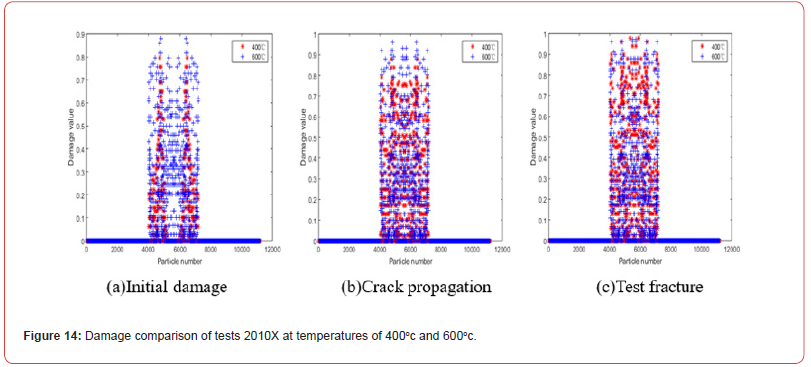
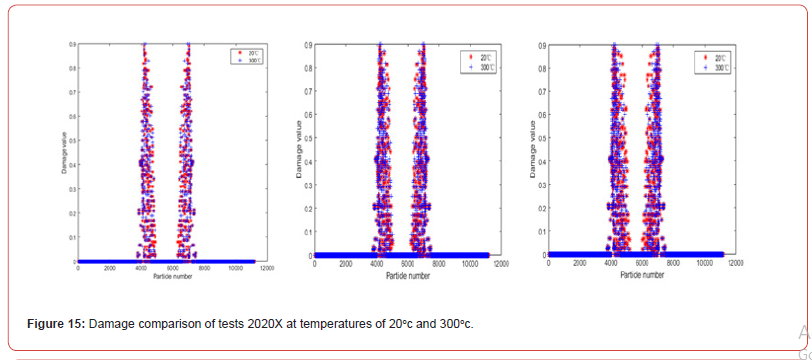
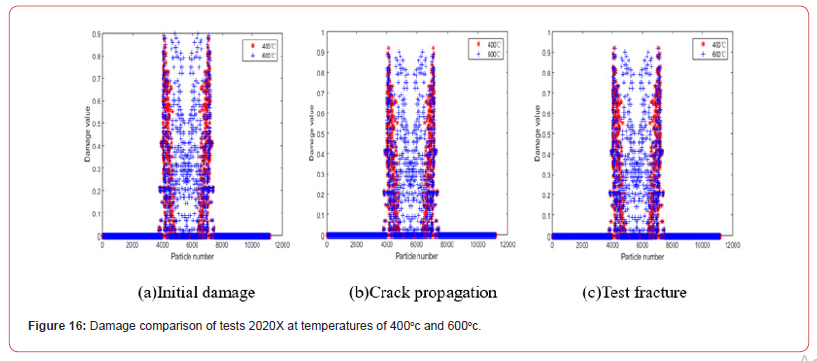
Figures 13&14 show the damage comparison of test 2010X at different temperatures. At the initial damage stage, the damage value of the test with high temperature is high, and the damaged area of the test is large. Figure 13 shows that before 300℃, the two cracks only propagate in the horizontal direction, while Figure 14 shows that after 300℃, the horizontal propagation path of the two cracks decreases and expands to the middle region of the crack as the temperature increases. With the loading, the damage occurred in the middle region of the two cracks of the test, and the damage value increased with the temperature increasing. When the crack breaks, the damage values of tests under different temperature conditions are the same, and there are more particles damaged when the damage values of tests at high temperature approach 1.0. Figures 15&16 show the damage comparison of tests under different temperature conditions at 2020X. In tests with longitudinal spacing between bilateral cracks of 20mm, the damage values of tests at different temperatures at the same time are the same as the temperature increases, and the bilateral cracks of tests extend horizontally without affecting each other before the temperature reaches 400℃, as can be seen from the damage of tests at 400℃ shown in Figure 15(a)-15(c) and Figures 16(a)-16(c). When the temperature reached at 600℃, obvious damage appeared in the middle of the two cracks, and the number of damaged particles increased.

In this paper, the law of material properties of steel structures changing with temperature is introduced into PD at different temperatures, and then PD parameters and constitutive equations varying with temperature are derived. The crack growth path of bilateral crack tests was understood through experiments, and the mechanism of bilateral crack damage and crack propagation at 20℃, 300℃, 400℃ and 600℃ was analyzed by applying force load with PD constitutive equation under the action of temperature.
a. The elastic modulus of steel has little change before the temperature is 300℃. When the temperature exceeds 300℃, the decline of elastic modulus is relatively increased; when the temperature reaches 600℃, the steel loses the bearing capacity.
b. At 20℃, the test with a longitudinal spacing of 0mm expanded into a horizontal crack, and the test with a longitudinal spacing of 10mm first expanded along the horizontal and then formed a 45° oblique crack. The two cracks of the test with a longitudinal spacing of 20mm did not affect each other and extended through the test in the horizontal direction.
c. With the temperature increasing, the local damage enlarges at the crack fusion locations of the tests with bilateral cracks with different longitudinal spacing, indicating that the temperature increase, reduces the shear resistance of steel and expands the damaged area of the tests.
d. By comparing the damage locations and damage values of three tests at different temperature, it can be seen that temperature has a great influence on the damage rate and damage value of tests, and with the temperature increase, the damage rate and damage value of tests also increases.

This article was supported by two foundations: 1. The Graduate First-class Curriculum Cultivation Project of Nanjing Forestry University. Project number: 163330008. 2. The research on crack propagation of bolt joints in steel structures based on Peridynamics of China Construction Seventh Division (Shanghai) Co., LTD. Project number: CSCEC-2022- Z-10.

1. GU Jin (2013) Mechanical behaviors study on the pyramid space truss in non-uniform temperature distributions. Nanjing Tech University, Nanjing, China.
2. Liu Yunhua, Xie Youjun, Long Guangcheng (2007) Progress of research on self-compacting concrete. Journal of the Chinese Ceramic Society 35(5): 671-678．
3. Aitcin PC (2003) The durability characteristics of high performance concrete: a review. Cement and Concrete Composites 25(4): 409-420.
4. Zhou Huanting (2006) Study on fire resistance of saddle cable net structure. Shanghai: Tongji University, Japan.
5. Xinhua Net (2020) The fire accident in Jinan Olympic Sports Center was caused by illegal operation.
6. Gao Yun, Zhang Hao, Yi Junnan (2009) Analysis on fire cause of high-rise building and fire safety counter measures. China safety science journal 10(6): 149-153.
7. Li Guaqiang, Han Linhai, Lou Guobiao, Jiang Shouchao (2006) Fire resistance design of steel structure and steel-concrete composite structure. Beijing, China Architecture and Building Press pp. 149-157.
8. IR Thomas, ID Bennetts (1992) Developments in the Design of Steel Structures for Fire. Journal of Construction Steel Research 23: 171-192.
9. (1980) International Standard ISO834, Fire-Resistance Tests-Elements of Building Construction, Amendment 1, Amendment 2.
10. MA Zhongcheng (1997) Damage assessment and seismic repair of reinforced concrete structures under fire. Harbin University of Civil Engineering and Architecture, Harbin, China.
11. JM Franseen, JB Schleich, LG Cajot, D Talamona, B Zhao, et al. (1994) A comparison betweeen fire structural fire codes applied to steel elements. Fourth International Symposium on Fire Safety Science, Ottawa pp. 1125-1136.
12. Yongjun Liu, Weicheng Fan, Hongnan Li (2004) Finite element method analysis of 3D temperature fields in structures subjected to fires. Proceedings of the Eighth International Symposium on Structural Engineering for Young Experts. Xi’an China pp. 592-596.
13. Dwaikat MMS, Kodur VKR, Quiel SE (2011) Experimental behavior of steel beam–columns subjected to fire-induced thermal gradients. Journal of Constructional Steel Research 67(1): 30-38.
14. Li Guoqiang, Chenchen (2011) Paremetric studies on critical temperature of restrained steel column in a fire.Journal of Disaster Prevention and Mitigation Engineering 31(06): 603-608.
15. Li Guoqiang, Chenchen (2012) Simplified calculation method for critical temperature of restrained steel column in fire.Journal of Disaster Prevention and Mitigation Engineering 32(01): 105-110.
16. Wang W, Liu B, Kodur V (2013) Effect of temperature on strength and elastic modulus of high-strength steel. Journal of materials in civil engineering 25(2): 174-182.
17. Wang W, Liu T, Liu J (2015) Experimental study on post-fire mechanical properties of high strength Q460 steel. Journal of Constructional Steel Research 114: 100-109.
18. Jiang Yaqiang, Wang Liangwei, Zhong Bo (2020) Full scale test on anti-collapse performance of a single-story steel portal frame in real fire. Journal of Building Structures 41(4): 51-58.
19. Lu C, Lin T, Cao J (2021) Microstructure evolution and fire-resistant properties of 690 MPa anti-seismic fire-resistant steel plate[J]. Materials Research Express 8(6): 066523.
20. Wk A, Uks A, Ms B (2021) Mechanical properties of conventional structural steel and fire-resistant steel at elevated temperatures. Journal of Constructional Steel Research 181: 106615.
21. Wu Y, Xu Y, Shi Y (2019) Overall buckling behavior of fire-resistant steel welded I-section columns under ambient temperature. Journal of Constructional Steel Research 157(7): 32-45.
22. Shi WL, Ding SM, Wang YB (2023) Experimental study on residual stress of fire-resistant steel welded box-sections. Journal of Constructional Steel Research 206(3): 109730.
23. Chen W, Ye J (2021) The most adverse fire scenario research of steel frame structure fire-resistant design based on structural vulnerability analysis 34: 2861-2875.
24. Lou GB, Fei CN, Wang YB (2022) Experimental study on post fire mechanical properties of high strength fire resistant steel. Engineering Mechanics 39(09): 153-159.
25. Wang WY, Zhang YH, Li GQ (2022) Study on nominal values of mechanical properties of high strength steel at elevated temperature and after fire exposure. Journal of Building Structures 43(09): 138-150.
26. Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. Journal of Mechanics Physics of Solids 48(1): 175-209.
27. Silling SA, Epton M, Wechner 0, Xu J, Askari E (2007) Peridynamic states and constitutive modeling. J Elasticity 88: 151-184.
28. Bahattin K, Erdogan M (2009) Coupling of peridynamic theory and finite element method [M]. American Institute of Aeronautics and Astronautics.
29. Zhao J, Tang H, Xue S (2018) A new fracture criterion for peridynamic and dual-horizon peridynamics. Frontiers of Structural and Civil Engineering 12(4): 629-641.
30. Zhao J, Tang H, Xue S (2018) Peridynamics versus XFEM: a comparative study for quasistatic crack problem. Frontiers of Structural and Civil Engineering 12(4): 548-557.
31. Zhao J, Li T, Dou X (2021) Crack propagation with different radius local random damage based on peridynamic theory. Frontiers of Structural and Civil Engineering 15(5): 1238-1248.
32. Zhao J, Gao H, Guo X (2021) A numerical study of crack propagation with variable temperature in steel structures using peridynamic constitutive model. International Journal of Hydromechatronics 4(2): 116-141.
33. Zhao J, Li T, Dou X (2018) Analysis of the center parallel double-crack propagation with initial casting defects by peridynamics. Journal of Harbin Engineering University 39(10): 1612-1616.
34. Rabczuk T, Zi G, Bordas S (2010) A simple and robust three-dimensional cracking-particle method without enrichment. Computer Methods in Applied Mechanics & Engineering 199(37-40): 2437-2455.
35. Rabczuk T, Belytschko T (2007) A three-dimensional large deformation meshfree method for arbitrary evolving cracks. Computer Methods in Applied Mechanics and Engineering 196(29-30): 2777-2799.
36. Rabczuk T, Belytschko T (2004) Cracking particles: a simplified meshfree method for arbitrary evolving cracks//World Congress on Computational Mechanics 61(13).
37. Rabczuk T, Zi G, Stéphane Bordas (2008) A geometrically non-linear three-dimensional cohesive crack method for reinforced concrete structures. Engineering Fracture Mechanics 75(16): 4740-4758.
38. Ren HL, Zhuang XY, Anitescu C (2019) An explicit phase field method for brittle dynamic fracture. Computers & Structures 217: 45-56.
39. Demmie PN, Silling SA (2007) An approach to modeling extreme loading of structures using peridynamics. Journal of Mechanics of Materials and Structures 2(10): 1921-1945.
40. Bobaru F, Zhang G (2015) Why do cracks branch? A peridynamic investigation of dynamic brittle fracture. International Journal of Fracture 196(1): 59-98.
41. Peddakotla SA, Yuan J, Minisci E (2023) A numerical approach to evaluate temperature dependent peridynamics damage model for destructive atmospheric entry of spacecraft, Aeronautical Journal 127(1309): 398-427.
42. Wang BQ, Oterkus S, Oterkus E (2020) Thermal diffusion analysis by using dual horizon peridynamics. Journal of Thermal Stresses 44(1): 51-74.