Mode I Crack Propagation in Concrete Structures under Impact Loadings

This paper does not present new experimental research and new results about the problem of concrete constructions behavior under impact loadings. The objective is to consider several existing results from literature and to analyze them to propose a strategy of modeling related to impact loadings. A large majority of concrete constructions fails under impact loadings due to excessive tensile stresses. Several experimental research have been carried out, in the past, for studying the strain rate effect on concrete specimens under uniaxial tensile stresses [1-8]. It is useful to give the orders of magnitude of the stress and strain rates generated by impact loadings in conventional civil engineering structures. These stress rates typically range from 10-2 to 1000 GPa.^-1, which corresponds to strain rates ranging from 10-3 to 100 ^-1. To be more precise, most of the situations in which concrete constructions are subjected to impact loadings correspond to tensile stress rates that rarely exceed 100 GPa.^-1. Previous experimental research, using Hopkinson bars, were capable to reach these levels of tensile stress rates [1, 3-9].

These physical mechanisms were deeply explained in previous papers [4,9]. One of the main results of the research carried out to study these rate effects is that they are mainly linked, in a stress rates domain between 5-10-2 and 100 GPa.s-1, to the presence of evaporable water within the nanopores of the hydrates of the concrete. The influence of the type of concrete aggregates is considered as negligible [9]. Another important experimental result is related to the fact that, for a fully dried concrete, no strain rate effect is observed when this strain rate is between 0.5 and 1.25 s-1 [1]. This result is illustrated in Figure 1. So, this result indicates that, until stress rates around 100 GPa.s-1, no inertial effects exist inside a concrete specimen in tension (Figure 1).

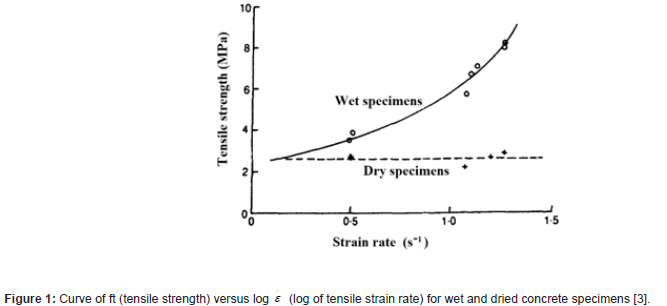
An assumption has been put forward concerning the physical mechanism having as its main actor this evaporable water. It is a mechanism similar to the Stefan effect and involving the viscosity of water. This Stefan effect (well known in physics) can be summarized as follows: when a thin film of a viscous liquid is caught between two perfectly flat plates which are moved apart from one another with a certain rate, this film exerts a restoring force on the plates proportional to the displacement rate of the plates.

This mechanism is expressed in relation (1):

Where:
F is the restoring force,
η, the viscosity of the liquid,
h, the initial distance between the two plates,
h, the displacement rate of the two plates (> 0),
and V the volume of the liquid.

If the assumption that the free water existing within hydrates (assimilated here to a network of plates) is at the origin of a mechanism of this type, it can be easy to understand why the rate effects are important in wet concrete. Obviously, this Stefan effect has to be considered as an explanatory model that allows understanding and not as a quantitative approach of the rate effects. From the tensile cracking process of concrete in quasi-static regime, the viscous mechanism, related to the Stefan effect, is as follows: before microcracks localization (leading to macrocrack appearance), the viscous mechanism can have two consequences:
1. to delay the creation of microcracks,
2. to delay the propagation of initial microcracks existing in concretes before mechanical loadings (due to autogenous shrinkage).

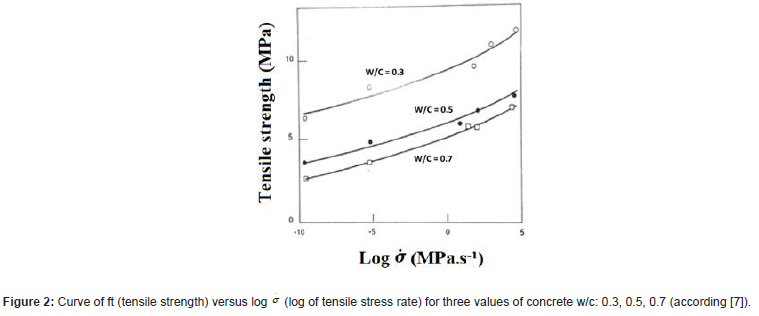
These two actions lead, on the one hand, to delay the localization of the microcracking, and therefore, to increase the tensile strength. It should be noted here that the Stefan effect has a lot of more influence on the strength than on the Young’s modulus because, for this last parameter, the aggregates, which play an important role, are not, or only very slightly, affected by the viscous mechanism [9]. As all the concretes, independently of their mix design, have mainly the same quantity of evaporable water within their nanopores, in absolute value, so the increase of tensile strength with a strain rate (or stress rate) should be the same for all concretes. This assumption is confirmed by an experimental work made, in the past, by two European research teams on the tensile rate effects of different concretes [7]. Figure 2 presents the main results obtained during this experimental work (Figure 2).

From this Figure 2, it is possible to draw a curve connecting the tensile strength increasing with the logarithm of the stress rate (Figure 3).

A look of this Figure 2 leads to the following remarks and conclusions: the evolution of the tensile strength in function of the logarithm of the stress rate is closed to a linear one.

From Figure 3, the following relation can be proposed:

Where:
f_tstat is the static tensile strength,
f_tdyn is the dynamic tensile strength,

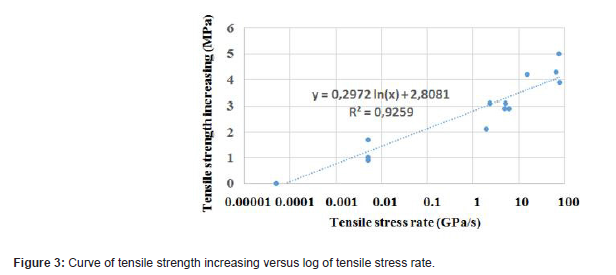
σ is the tensile stress rate.
The strong assumption arising from this chapter is that relation 1 is considered as valid for all concretes (without fibers, of course).

Chapter II leads to the following conclusions (or assumptions):
1. Inertial effects do not exist in concrete specimen under impact loadings until tensile stress rates of 100 GPa.s-1. That corresponds to numerous concrete constructions behaviour.
2. Viscous phenomena linked the presence of evaporable water within the nanopores of the concrete hydrates constitutes the main physical origin of strain rate effects until tensile stress rates of 100 GPa.s-1. This phenomenon leads to the existence of a unique relation relevant for all concretes linking the evolution of the tensile strength in function of the logarithm of the tensile stress rate (relation 1).

When uniaxial tension behaviour is concerned, three main steps exist (that are well known and considered as basis knowledge):
1. Before the peak load corresponding to the tensile strength, the cracking process is related to diffuse microcracking.
2. The peak load is reached when a localization of the microcracks to create a macrocrack appears.
3. After the peak load corresponding to the softening behaviour of the concrete, the propagation of the macrocrack occurs.

In terms of modeling, the above conclusions and remarks permit to make strong simplifications concerning the numerical models to develop for treating the problem of concrete constructions behaviour under impact loadings. The first simplification is related to the fact that the inertial effect has not to be considered. Thus, a simple time discretization algorithm of the problem, as, for example, the classical Newmark one, permits to determine time by time, during the computing, the stresses rate field. The second type of simplification will depend on the numerical model used to treat the concrete tensile behaviour. In this paper, the models concerned are those considering a perfect brittle rupture of concrete in tension. It means, that the cracking process is, in these models, is the result of the creation of elementary failures that appear and coalesce to form the macroscopic cracks that propagate. In this family of model, the use of relation (1) gives the main material parameter to consider in the computing. Among this family of models, it is essential to cite the lattice models [10-12] or the probabilistic explicit cracking model [13-15].

The present paper is on a new analysis of previous works related to the concrete tensile behaviour under impact loadings.

This analysis permits to conclude that:
1. Inertial effects do not exist in concrete specimen under impact loadings until tensile stress rates of 100 GPa.s_-1.
2. Viscous phenomena linked the presence of evaporable water within the nanopores of the concrete hydrates constitutes the main physical origin of strain rate effects until tensile stress rates of 100 GPa.s_-1. This phenomenon leads to the existence of a unique relation relevant for all concretes linking the evolution of the tensile strength in function of the logarithm of the tensile stress rate.

These conclusions lead to propose a strategy of modeling the behaviour of concrete construction under impact loadings. The models concerned by this strategy are that consider concrete cracking process as the result of the creation of elementary brittle failures that appear and coalesce to form the macroscopic cracks that propagate.

None.

No conflict of interest.

1. Reinhardt HW (1982) Concrete under impact loading tensile strength and bond. Heron 27(3): 5-48.
2. Banthia NP, Mindess S, Benthur A (1987) Effect of impact loading on the properties of concrete. Proceedings of 1^st International RILEM Congress, Paris, edited by JC Maso, Chapman and Hall, pp.1033-1040.
3. Reinhardt HW, Rossi P, Van Mier JMG (1990) Joint investigation of concrete at high rates of loading. Mater Struct 23: 213-216.
4. Rossi P (1991) Physical phenomenon which can explain the mechanical behaviour of concrete under high strain rates. Materials and Structures 24: 422-424.
5. Rossi P (1991) Influence of cracking in the presence of free water on the mechanical behaviour of concrete. Magazine of Concrete Research 43(154): 53-57.
6. Rossi P (1994) Dynamic behaviour of concrete: from material to the structure. Materials and Structures 27: 319-323.
7. Rossi P, Van Mier JGM, Toutlemonde F, Le Maou F, Boulay C (1994) Effect of loading rate on the strength of concrete subjected to uniaxial tension. Materials and Structures, 27: 260-264.
8. Toutlemonde F, Rossi P (1995) Characterisation of microconcrete in dynamics: material in tension and compression, structures under flexure. Engineering Structures Special Publication.
9. Toutlemonde F, Rossi P (1995) Effect of loading rate on the tensile behaviour of concrete: description of the physical mechanisms. Materials and Structures 29(186): 116-118.
10. Schlangen E, Van Mier JGM (1992) Simple lattice model for numerical simulation of fracture of concrete materials and structures. Materials and Structures, 25: 534–542.
11. Berto S, Bolander JE (2006) Crack model of fracture in irregular lattices. Computer Methods in Applied Mechanics and Engineering 195(52): 7172-7181.
12. Cusatis G, Pelessone D, Mencarelli Figini A (2011) Lattice Discrete Particle Model (LDPM) for failure behavior of concrete. I: Theory. Cement and Concrete Composites 33(9): 881-890.
13. Rossi P, Richer S (1987) Numerical modelling of concrete cracking based on a stochastic approach. Materials and Structures 20: 334-337.
14. Rossi P, Wu X (1992) Probabilistic model for material behaviour analysis and appraisement of concrete structures. Magazine of concrete research 44(161): 271-280.
15. Rossi P, Ulm FJ, Hachi F (1996) Compressive behaviour of concrete: physical mechanisms and modeling. Journal of Engineering Mechanics 122(11): 1038-1043.