 Research Article
Research Article
Determination of Toughness Characteristics of Concretes
Pierre Rossi*
Pierre Rossi Consulting, 15 rue Louis Bonnet, 75011, Paris, France
Pierre Rossi, Pierre Rossi Consulting, 15 rue Louis Bonnet, 75011, Paris, France.
Received Date:May 12, 2023; Published Date:May 24, 2023
Abstract
This paper is on experimental works related to the determination of concretes toughness characteristics (KIC and GIC in the framework of Linear Fracture Mechanics theory), in mode I of cracking. They are determined by performing fracture mechanic test on very large DCB (Double Cantilever Beam) specimens. In parallel, and for the same concretes, splitting tensile and compressive strengths are determined by performing tests on standardized cylindrical specimens. The interest of this work is 1) to propose intrinsic (and not scale effect sensitive) values of toughness characteristics related to three very different concretes (whose an ultra-high strength concrete) 2) to propose load-notch opening curves related to mode I macrocrack propagation over more than one meter. These last experimental results are very useful to validate numerical models devoted to fracture mechanics of concrete.
Keywords:Concretes; Fracture Mechanics Test; Toughness Characteristics; Tensile Splitting Strength; Compressive Strength
Introduction
Some numerical models, related to mode I cracking of concretes, use toughness parameter as KIC or GIC (in the framework of Linear Fracture Mechanics theory) as main material characteristic [1-3]. The principal problem is the difficulty to determine experimentally these toughness characteristics. Indeed, it has been clearly demonstrated that experimental tests have to be performed on large concrete specimens to get it [1, 4-14]. This is due to the high level of heterogeneity of concrete linked to the larger aggregate size. Thus, the dimension of the process zone at the macrocrack front tip which propagates reaches about 30 cm [14]. In the past, this type of test on large Double Cantilever Beam (DCB) specimen was performed [11, 13, 14]. This DCB specimen had the following dimensions: 3.5m long, 1.1m large and 0.3m width.
It is important to point out that this DCB test on very large spec imen is the only one performed on current concretes (with larger aggregate diameter larger than 10 cm and without fibers) that allowed to get real and intrinsic values of KIC or GIC [11-14]. It means that the large majority of the others experimental studies led to KIC or GIC that was not intrinsic but scale effect sensitive [11-14]. This type of DCB test on so huge specimen being difficult to perform and time consuming, only one concrete, called concrete 1 in this paper, was studied [11,13,14]. In parallel to this DCB test, 6 standardized compressive and splitting tests (Brazilian tests) were performed on 16 cm (diameter) x 32 cm (length) cylindrical specimens [14]. The objective of the present work is to perform the same program of tests (DCB, compressive and Brazilian tests) on two more concretes very different compared with the previous one and try to find general relations between toughness parameters and tensile and compressive strengths.
Previous experimental test on large DCB specimen
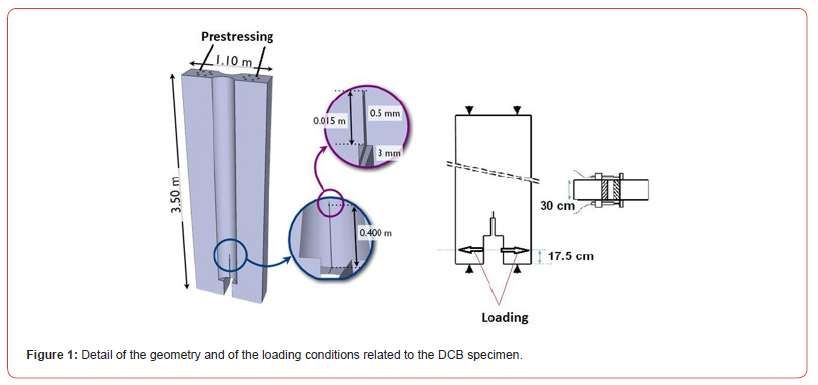
The geometry and the loading conditions are given in Figure 1.
The test is controlled by applying a constant notch displacement rate of 25 μm/min. The test is fully detailed in [11, 14]. The load/ notch opening curve is recorded during the test. After the peak load, that corresponds to the macrocrack initiation, several notch closing/ opening cycles are imposed at the same frequency. These cycles permit to follow the stiffness evolution of the specimen that is used to calculate KIC (mode I critical intensity factor) and GIC (mode I specific fracture energy) using the classical and well known (in linear fracture mechanics theory) compliance method [11-16].
Table 1 presents the concrete 1 mix design [11, 13, 14]. The average compressive, fc, and splitting tensile strengths, fts, of concrete 1 are given in Table 2.
Table:1Concrete 1 mix design.

Table:2Average compressive and splitting tensile strengths of concrete 1.

*The average young modulus was determined during the compressive tests.
Figure 2 presents the load/notch opening curve related to concrete 1. The analysis of the DCB test by using the compliance method leads to get KIC versus equivalent crack length curve. This equivalent crack length is the idealized crack length (straight and smooth crack in a linear elastic material) that leads to the same specimen compliance than the experimental one. Very commonly, the evolution of the specimen compliance with the idealized crack length (analytical relation) is obtained by performing linear elastic finite element analysis [11,13,14].
In figure 3, this KIC versus equivalent crack length curve related to concrete 1 is presented. In this Figure, it can be noted that KIC fluctuates between a minimum and a maximum with a constant evolution. This fluctuation is the result of the material heterogeneity. The fact that a constant evolution of KIC with the equivalent crack length is observed proves that the DCB specimen used is large enough to get characteristic KIC value. In other words, the length of the crack propagation is so large, more than 1.0 m, that one DCB test is sufficient to get a precise information about the dispersion related to KIC of a given concrete. It is not necessary, as for others concrete mechanical characteristics, to perform several tests. From the KIC fluctuation a mean value can be easily determined (Figure 3).
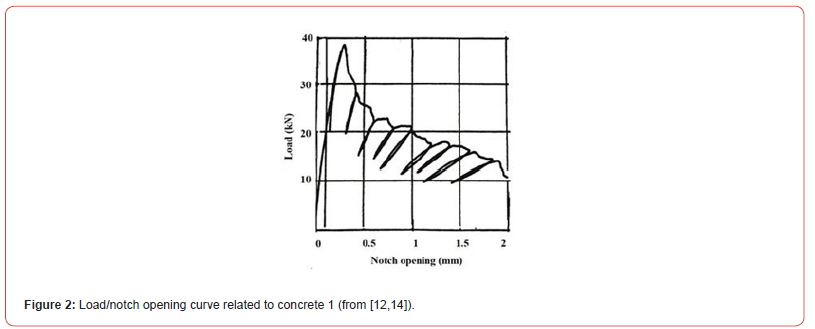
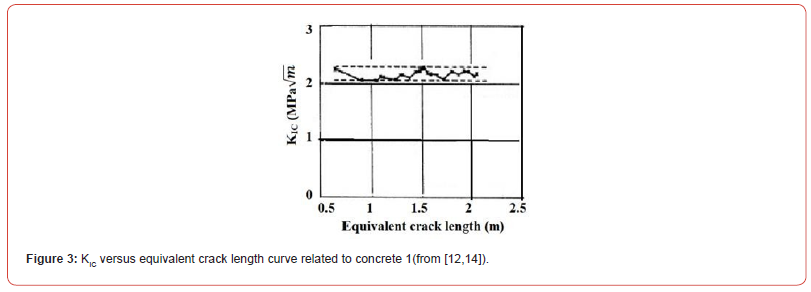
Table:3KIC and GIC mean values related to concrete 1.

KIC and GIC mean values related to concrete 1 are presented in Table 3.
Note that the relation between KIC and GIC is very well known in Linear Elastic Fracture Mechanics:
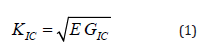
This relation (1) is relevant for stresses plane conditions that is the case with the DCB specimen.
Experimental Campaign on Other Concretes
The same program of tests, described in chapter I, have been performed in this new experimental campaign. The mix design of these two concretes, concrete 2 and concrete 3, are given in table 4.
The average compressive and splitting tensile strengths and young modulus of concretes 2 and 3 are given in Table 5.
Table:4Mix designs of concretes 2 and 3.
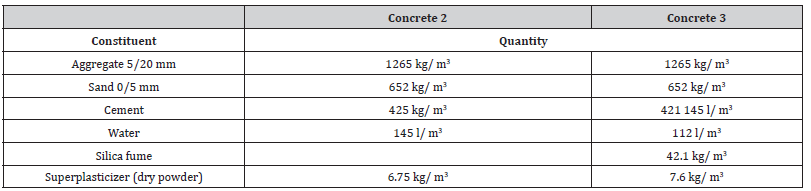
Table:5Average compressive and splitting tensile strengths and young modulus of concretes 2 and 3.

Table:6KIC and GIC mean values related to concretes 2 and 3.

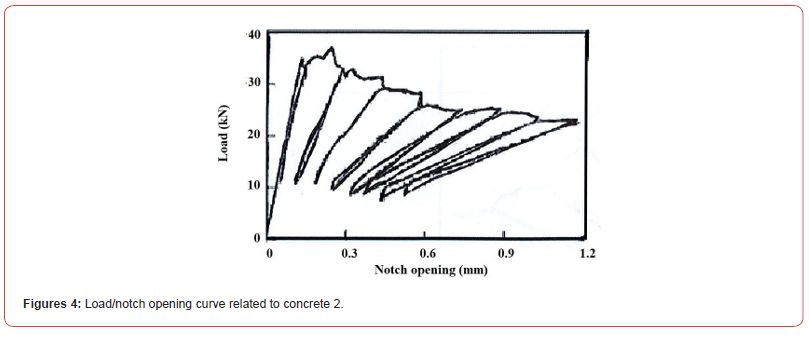
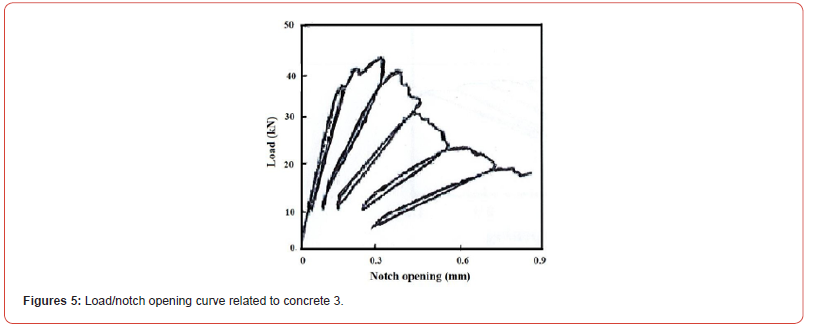
Figures 4 and 5 present the load/notch opening curves related respectively to concrete 2 and 3. KIC and GIC mean values related respectively to concretes 2 and 3 are presented in Table 6.
Analytical relations between toughness characteristics and splitting tensile and compressive strengths
From tables 2, 3, 5 and 6, it is interesting to draw the following
curves:
KIC versus fts and fc.
GIC versus fts and fc.
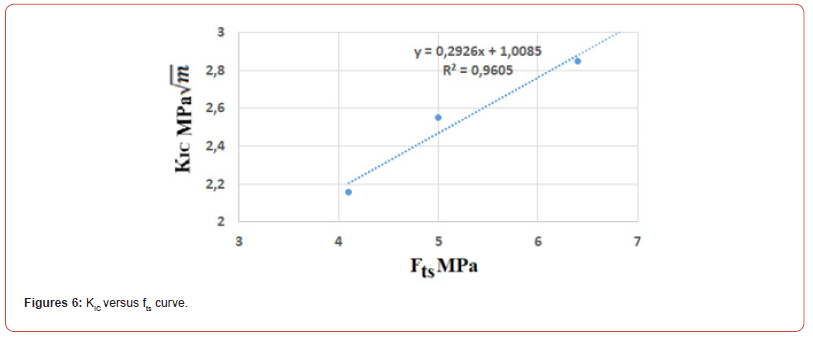
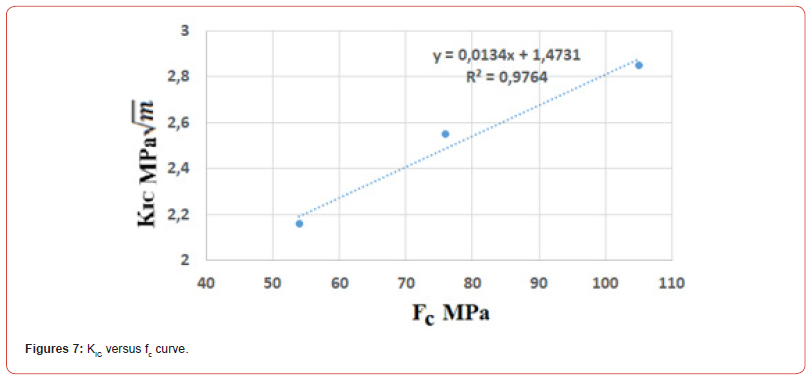
Figures 6 and 7 present respectively the curves KIC versus fts and KIC versus fc.
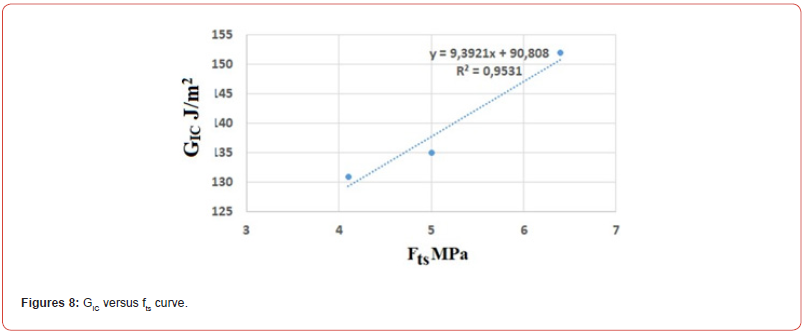
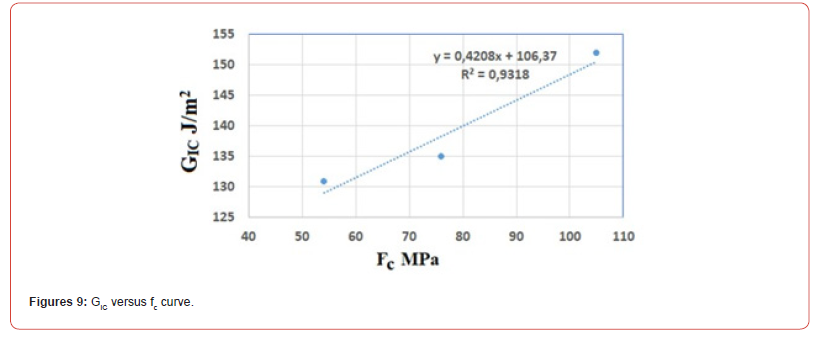
Figures 8 and 9 present respectively the curves GIC versus fts and GIC versus fc. From Figures 6 to 9, it appears that the links between KIC and GIC with fts and fc. are strong. From curves 6 to 9 the following relations can be proposed:
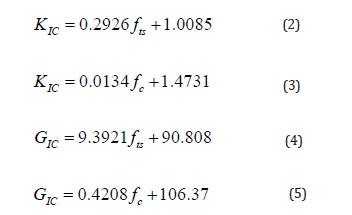
All these relations above being the consequence of experimental imprecisions, it is acceptable to simplify them as following:
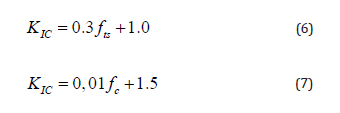
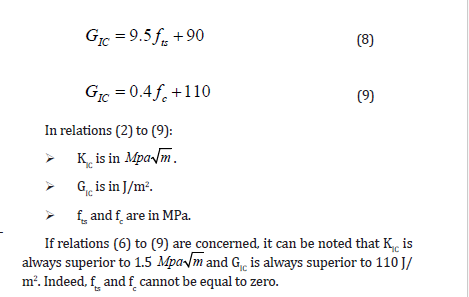
It is important to recall that these relations have been determined for concretes having:
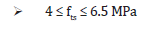

Discussion
It can be argued that making a direct link between toughness and compressive or tensile strength is too simplistic because other parameters than compressive (or tensile) strength influence this toughness, such as, for example, the water/cement ratio or the larger aggregate size. In fact, this link is possible and relevant because the physical mechanisms at the origin of these three mechanical characteristics are similar. Indeed, these three mechanical characteristics are the result of the passage from a diffuse microcracking to a localized macrocracking, it means the localization process of the cracking. This is obvious and well known for the compressive and the tensile strengths. Concerning KIC or GIC, it exists a microcracked zone at the front tip of the macrocrack in propagation, called process zone. The macrocrack can propagate only when the total dissipative energy in this process zone (microcracked zone) is achieved. The fact that parameters like water/cement ratio and larger aggregate have the same type of influence on the localization process related to the three mechanical characteristics can explain the good correlation between them and the linear relations obtained, even only three points are concerned. There are no physical and mechanical reasons that prevent extending the domain of validity of relations (6) to (9) to concretes having smaller compressive and tensile strengths. On the other hand, these relations are not valid for fibre reinforced concretes [12].
To conclude this chapter on discussion, it can be affirmed without any ambiguity, that the use of the analytical relations 6 to 9, as simplistic as they are, leads to a better prediction of the toughness of a given concrete than the usual use of small (a lot of smaller than the DCB specimen of the present study) laboratory test specimens.
Conclusion
This paper is related to experimental works concerning the
possible link between toughness characteristics (KIC and GIC, determined
by performing fracture mechanic test on large DCB specimens)
and splitting tensile and compressive strengths (determined
by performing tests on standardized cylindrical specimens) of several
concretes. These experimental works were carried out during
two campaigns of test:
A past one, yet published, on one type of concrete.
The present one on two more and different concretes.
These campaigns of test have the following interests:
They permit to get intrinsic values of the toughness (defined
in the framework of the Linear Fracture Mechanics) of three
different concretes with different mechanical properties (compressive
and tensile splitting strengths).
They propose load-notch opening curves related to mode
I macrocrack propagation over more than one meter. These results
are very important and useful for researchers who want to validate
their numerical models related to this problem.
They propose to engineers and/or researchers, using numerical
models based on fracture mechanics, simple analytical relations
permitting to get real and intrinsic KIC and GIC values from
simple and standardized tests.
Acknowledgment
None.
Conflict of Interest
No conflict of interest.
References
- Hillerborg A, Modéer M, Petersson PE (1976) Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and concrete research 6: 773–781.
- Gálvez JC, Červenka J, Cendón DA, Saouma V (2002) A discrete crack approaches normal/shear cracking of concrete. Cement and Concrete Research pp.1567-1585.
- Rastiello G, Tailhan JL, Rossi P, Dal Pont S (2015) Macroscopic probabilistic cracking approach for the numerical modelling of fluid leakage in concrete. Annals of Solid and Structural Mechanics 7(1-2): 1–16.
- Entov VM, Yagust VY (1975) Experimental investigation of laws governing quasi static development of crack in concrete. I 2V. AN. SSSR. Mekhnica, Tvergo, Tela 10(4): 93-103.
- Watson RL (1978) The estimation of fracture energy as a measure of toughness of hardened cement paste. Cement and Concrete Research 8: 651-556.
- Wittman FH (1981) Mechanisms and mechanics of fracture of concrete. ICF 5 Cannes 4: 1467-1487.
- Walsh PF (1982) Fracture of plain concrete. Indian Concrete Journal pp.469-476.
- Carpinteri A (1982) Experimental determination of fracture toughness KIC for aggregative materials. Advances in Fracture research (fracture 81), D. François, Pergamon Press, Oxford 4: 1491-1498.
- Shah SP (1984) Application of fracture mechanics to cementitious materials. Preprints of the proceedings NATO Advanced Workshop, Northwestern University, Evanston.
- Reinhardt HW (1986) The role of fracture mechanics in rational rules for concrete design. Iabse Reriodica 1.
- Rossi P, Acker P, Francois D (1984) Measurements of the Fracture Toughness KIC of Concrete. Proceeding of the 6th International Conference on Fracture, New Delhi, p.2839.
- Rossi P (1991) Fracture properties of concrete are determined by means of wedge splitting tests and tapered double cantilever beams tests. Fracture mechanics test methods for concrete. In: Shah S, Carpinteri A (Eds.) RILEM report 5, Chapman and Hall, CRC Press.
- Rossi P, Coussy O, Boulay C, Acker P, Malier Y (1986) Comparison between plain concrete toughness and steel fibre reinforced concrete toughness. Cement and Concrete Research 16: 303-313.
- Rossi P (1986) Cracking of concrete-from material to structure: application of fracture mechanics [dissertation]. National School of Bridges and Roads, France, in French.
- Okamura H, Watanabe K, Takano T (1973) Applications of the Compliance Concept in Fracture Mechanics. Progress in Flaw Growth and Fracture Toughness Testing. In: Kaufman J, Swedlow J, Corten H, Srawley J, Heyer R, et al. (ed.) West Conshohocken, PA: ASTM International, pp. 423-438
- Jablonski DA, Journet B, Vecchio RS, Hertzberg R (1985) Compliance functions for various fracture mechanics specimens. Engineering Fracture Mechanics 22(5): 819-827.
-
Tianzhong Ma, Xiaohui Yang, Weixiong Zhang, Chendong Sun. Catastrophic Mechanism and Stability Analysis of Jiangdingya Landslide in Zhouqu County, Gansu Province, China. Cur Trends Civil & Struct Eng. 7(3): 2021. CTCSE.MS.ID.000729.
-
Concretes, Fracture Mechanics Test, Toughness Characteristics, Tensile Splitting Strength, Compressive Strength
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
- Abstract
- Introduction
- Natural Geological Structure
- Evolution History of Landslide
- Development Characteristics of Jiangdingya Landslide
- Analysis of Catastrophe Mechanism of Landslides
- Stability Analysis of Landslide
- Safety Treatment of Landslide
- Conclusion
- Acknowledgement
- Conflicts of Interest
- References






