 Research Article
Research Article
Calculation of Dynamic Load Factor for Reinforced Concrete Slabs Subjected to Above Ground Explosion
Rohollah Rostami*, Slobodan B Mickovski and Nicholas Hytiris
School of Computing, Engineering and Built Environment, Glasgow Caledonian University, Glasgow, UK
Rohollah Rostami, School of Computing, Engineering and Built Environment, Glasgow Caledonian University, Glasgow, UK.
Received Date: February 09, 2020; Published Date: February 25, 2020
Abstract
One of the common methods for structural design against explosive loads is the static linear equivalent analysis. Multiplying the maximum value of the explosive load by the dynamic load factor (DLF), the method would yield a static load equivalent to the explosive load. With this, the dynamic analysis can be transformed into an equivalent static analysis which, in turn, can be carried out using the current codes and standards. The lack of a complete and comprehensive study for computing the DLF means that the engineers carry out their design based on approximation by applying the coefficient diagrams obtained for beams and considering the ratio of the explosive load run-time to the main period of the member vibration (td/T). The purpose of this paper is to present the dynamic coefficient (d) of concrete slabs with different ratios of vibration periods, different boundary conditions, and different aspect ratios to be used as a basis of design against explosive load on structures. In this regard, a range of concrete slabs were modelled with a maximum measuring unit of dynamic load (using Single-Degree-of-Freedom (SDOF) models under triangular load) and consequently, before a static load was applied. Then, by considering the maximum bending moments obtained from static and dynamic analyses, the dynamic coefficient (d) or DLF was derived for each structure. For this purpose, 1680 model runs, including both dynamic and static cases, were carried out. The findings from these were plotted and analysed in terms of the dynamic coefficient (d) vs. (td/T), for a range of boundary conditions. The results revealed variation trends in the value of the dynamic coefficient (d) for each slab under different boundary conditions and can be used in the development of enhanced and more realistic procedures for structural design against explosive loads.
Keywords: Explosive loads; Dynamic load factor (dlf); Concrete slab; Sdof model; Vibration
Introduction
The protection of buildings, petroleum or nuclear plants, and other infrastructure facilities against blast loads is an important design consideration aimed at increasing the safety and the blast resistance of the structure. Furthermore, in recent times, terrorist activities have resulted in extensive blast damage to civilian facilities and inflicted loss of life, social and economic impact [1- 5]. Consequently, the response of structures and their behaviour under and after explosive load, focusing on enhancing the blast resistance, has been of great interest in the past decade [6]. The behaviour of reinforced concrete (RC) structures subjected to explosive loads has been the topic of extensive research [3,6-8] resulting in proposal of design requirements. Furthermore, the dynamic response of structures has been shown to be affected by its configuration ACI370R-2014. Thiagarajan et al. [6] demonstrated that high strength concrete was very effective in reducing the level of response. Wang et al. [8] also observed that an increase in the explosive charge gradually changes the failure mode of RC slab from overall flexure failure to local punching failure.
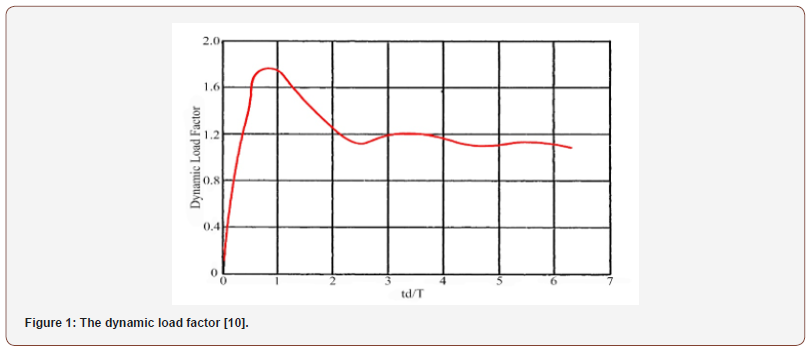
Various codes of practice [9-16], recommended the principles of explosion and strategies for design methods. The static linear equivalent analysis is one of the most utilized analytical design methods for RC structures against explosive loads that are typically governed by the dynamic load factor (DLF), the dynamic factor is the ratio of the dynamic deflection at any time to the static deflection which would have been caused under the maximum value of the load [9]. In this method, typically multiplying the maximum value of the explosive load by the DLF. The dynamic analysis transforms into an equivalent static analysis which can be carried out using the current codes and standards. However, due to lack of a complete and comprehensive study for computing the DLF, the design is carry out based on approximation by applying the diagrams obtained for beams and considering the ratio of the explosive load run-time to the main period of the member vibration (td/T) [10] (Figure 1).
However, based on this approach, in most cases, the applied explosive loadings can be with very small magnitude, which in the case of extreme events could be inadequate and not realistic. Therefore, further study and comprehensive consideration is necessary to predict more accurately the structural behaviour against explosive loads and, thereby, increase the safety and the level of robustness of the structure.
Blast Load
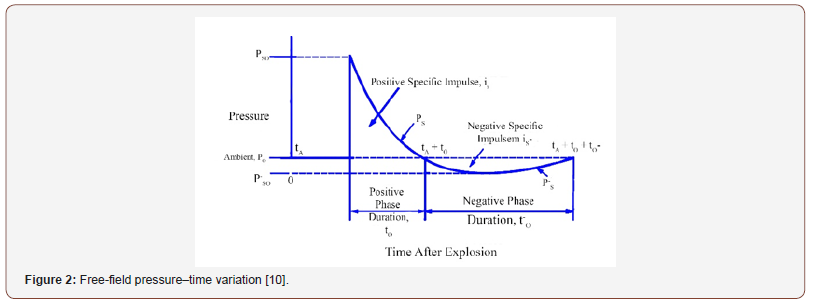
The blast load can be defined as a function of explosive sources, with a fast transition of a material from chemical reaction that propagates radially as a shock wave releasing a large amount of energy with high velocity [5]. The response of a structure or structural member subjected to a blast load must be determined for different explosives and conditions including explosive type, quantity, shape, and casing characteristics, geometry, thickness, material properties, location, and orientation with regard to any obstacles, as well as the relative position with regard to targets of concern [16]. An idealized shape of a shockwave pressure-time history for an open-air explosion is shown Fig. 2. The figure also shows blast pressures, load duration, impulse, shock wave velocity, arrival times, and other blast parameters. The shock front (at time ta) is essentially vertical, reflecting the sudden rise in pressure due to the explosion. The peak incident pressure Pso is at the end of this initial phase (rise time (tr)). The incident pressure (to) is the pressure on a surface parallel to the direction of propagation (such as a wall or a structure) (Figure 2).
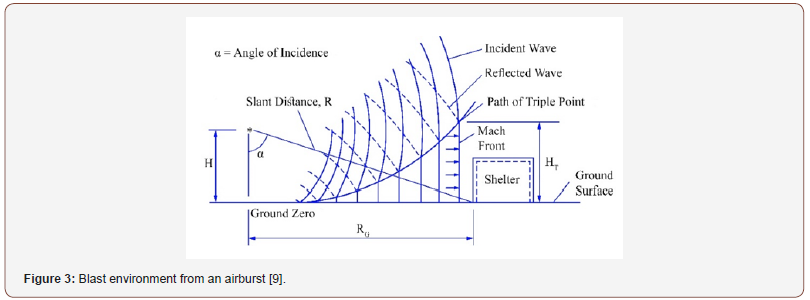
The airburst is produced by detonations which propagate through the atmosphere at a distance away from the structure and the initial blast wave, propagating away from the explosion, impinges on the ground surface prior to arrival at the structure (UFC 3-340-02). Figure 3 shows the blast environment from an airburst, in which the reflected wave and the incident wave (pressure) have the same general shapes. However, the peak of the reflected pressure is higher than that of the incident wave and depends on the incident wave and on the angle of the inclined surface (Figure 3).
The response of concrete structures to dynamic loads has been studied extensively in the past because the estimation of loading and predicting the response of a structure is one of the key responsibilities of a structural engineer.
Blast resistant design
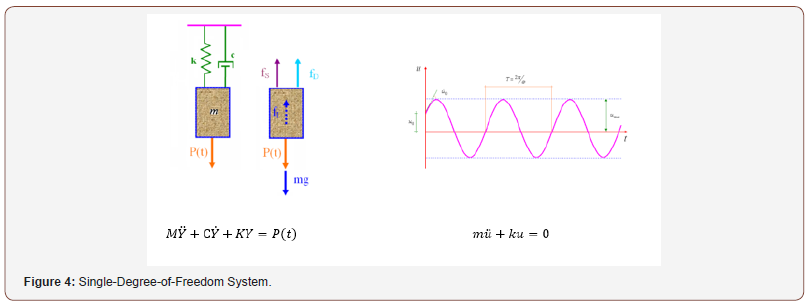
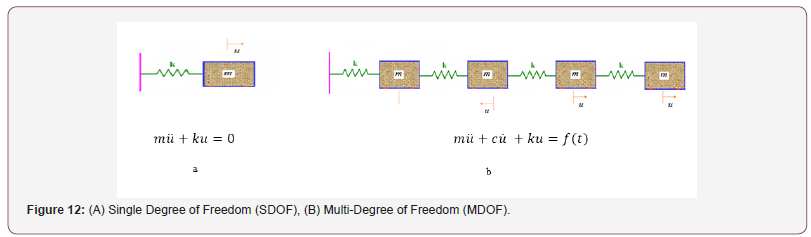
Different computational approaches are commonly employed for the design of structures against explosive loads such as the equivalent static method (ESM) and the single-degree-of-freedom (SDOF) model. The ESM embodies an approximate calculation which employs a static analysis using equivalent static loads derived from the dynamic load [7]. The equivalent static load is applied here to simulate the dynamic response and this method is sometimes called an “equivalent wind” approach [14]. This approach idealizes an entire structure or structural component as one point in the structure with a blast resistance at this point equivalent to the resistance of the entire structure. The SDOF approach considers the response of the idealized point under static conditions and its motion (displacement u or Y) as a linear elastic, damped singledegree- of-freedom system [17-20] characterized by their mass, M, the stiffness of the structure, K, and by viscous damping c. The response of many structures to blast loading can be adequately evaluated by system [14]. The underlying design principle in blastresistant design is that the exposed structural components should be designed to incur the same level of damage [21] throughout the structure’s load path. The blast-resistant design should aim to withstand the anticipated threats, minimize damage, and protect people; in this manner, RC slabs with an increased ductility offer the possibility to enhance the resistance for dynamic loading situations [16] (Figure 4).
Based on all these points, the present study aims to develop a simplified procedure to analyse RC slab structures subjected to above ground explosion in order to increase the structural robustness and resistance of structures against explosive loads. A comprehensive assessment using numerical modelling will be carried out to present the DLF of concrete slabs with different vibration period ratios, boundary conditions, and aspect ratios as a basis of design against explosive load on structures. Finite element analysis methods will be used in this study to evaluate the responses from linear and nonlinear calculated blast loads and compare them to the equivalent loading response, demonstrating that the proposed method can lead to more precise, accurate, quick, and, therefore, more reliable predictions.
Numerical Modelling
For the purpose of this study, the analysis is carried out using commercially available packages (SAP 2000 and ABAQUS 6.14), whereby both the static and dynamic analysis uses ABAQUS/Standard and ABAQUS/Explicit respectively. In order to parameterize the model and better reflect real-life scenarios, different geometry of the RC slab was modelled. The variations in geometry included: different aspect ratios (ratio of the length to the width) 1, 1.5, 2 and 3, whereby the smaller side and the slab thickness were always kept constant (4 m, and 0.25 m, respectively). The slabs were modelled as reinforced by steel bars in both directions and analysed for seven different vibration periods of the member vibration (td/T): 0.25, 0.5, 0.75, 1.00, 1.50, 2.00 and 4.00. By considering different combinations of the boundary conditions (fixed, pin, free), there were 30 models of RC slabs analysed in this study. The RC slabs were modelled using solid elements while the steel bars modelled using the wire option in the Abaqus. The blast loads were applied in the form of an equivalent triangular pressure pulse for air-blast loading provided in UFC 3-340-02, (2008). In the model, a vertical pressure was applied in the middle slab using an amplitude curve in Abaqus. The duration of the simplified triangle load curve where the load gradually increases from zero to 100 kN was modelled to be 5 ms. Then, in order to calculate the DLF, static and dynamic structural analysis is carried out using the same magnitude. This analysis resulted in values for the maximum bending moment. Using these values, the DLF was derived for each structure according to TM5-1300 [10] (Figure 5).
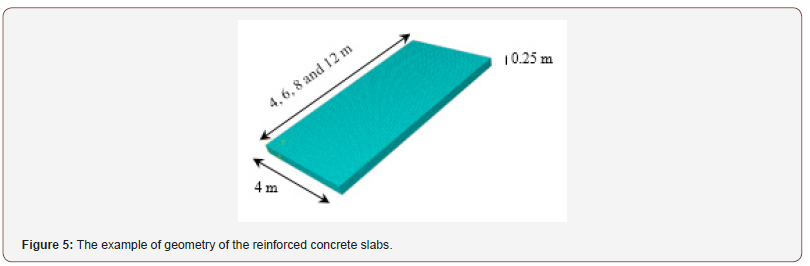
The parameterization and variation above resulted in a total of 1680 model runs, including both dynamic (840) and static (840) cases.
Concrete slabs models
RC slabs are widely present worldwide [22] they are used in different elements of building (depending on the location of the slab) due to the simple required formwork and reinforcement layout [23] and therefore straightforward repetitive construction procedure. Also, they are considered to be the most common structural members, which have been proven to be very effective and affordable in resisting blast loading [24]. Furthermore, RC is generally considered the most suitable and economically affordable construction material for blast resistant buildings, especially for those close to a potential blast source, relatively high overpressure and thermal effects in the event of an explosion [14] (Figure 6) (Table 1).
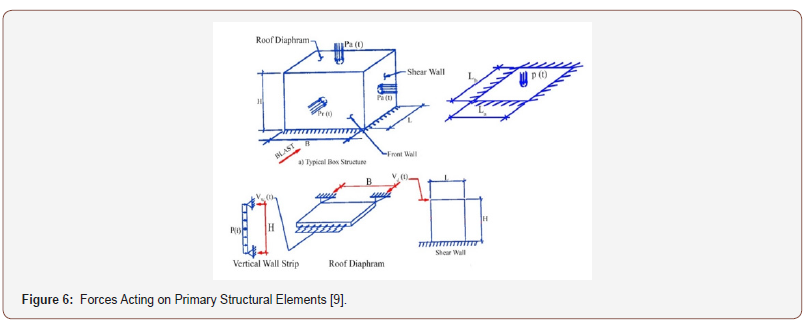
Table 1: Shapes of slabs with different boundary condition.
The modelled properties of the concrete slabs and reinforcement steel material are given in Table 2. They take into account the fact that the tension and compression strength of concrete increase with the loading rate [19,25-27], but also the fact that the tendency to pile up during such process can be attributed to the rate of dislocation and defect migration from inside the crystals (or grains) forming the material at the microscopic level to the grain boundaries [16]. Also, the modelled structures subjected to blast loads were typically allowed to undergo plastic (permanent) deformation to absorb the explosion energy [14]. One the other hand, the blast load was applied to structures very rapidly in a short period of time and a corresponding rapid rise in member stresses was expected. The total amount of blast energy required to be absorbed was modelled as a function of the peak load and duration of the blast. The adequacy of a blast loaded member was based on the maximum deformation rather than stress level (ASCE, 2010). Therefore, damping was neglected in this study (Table 2).
Table 2: Material properties of the modelled slabs and steel.

Blast loading
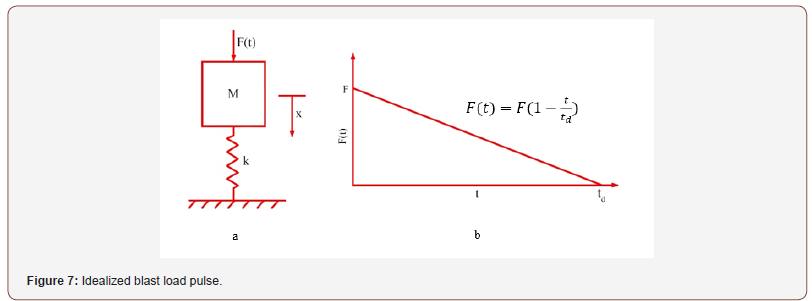
In order to assess the response of a blast-loaded structure (RC slab), in this study, the single degree of freedom (SDOF) approach was adopted. The principles of analysis can be represented as an equivalent SDOF system (Figure 7A), where the blast loading has been idealized as a force function F(t) in triangular shape (Figure 7B) delivering the peak force F during the positive phase duration of the blast load (td).
The equation of motion including the force function can be presented as (Equation 1):
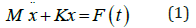
Where M is the mass of the RC slab (Figure 7)
The response of the RC slabs under blast load can be assessed in two stages. First, when the time of the blast shock wave duration is less than the positive phase duration, 0 < t ⩽ td, the solution for forced vibration of undamped system can be written as (equation 2; [28])
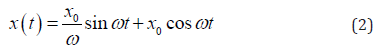
Where x(t) is the displacement function
The static deflection under the force F can be written as (Eq. 3 or Eq. 4):
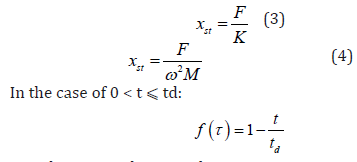
By substituting these conditions into Eq.2
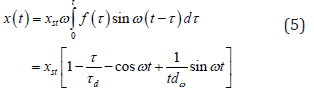
Finally, the equation 5 can be expressed as
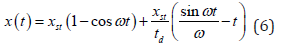
The dynamic load factor (DLF) can be defined as shown in Eq. (7) (TM5-1300, 1990)
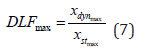
Where xdyn and xst are the dynamic and static displacements respectively. This dynamic load factor for the case (0 < t ⩽ td) can be written as Eq. (8)
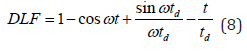
Secondly, when t>td, the displacement and dynamic load factor of the structural element can be written as a modal superposition, as shown in Eqs. (9) and (10)
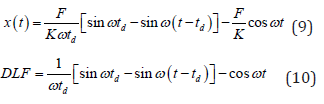
Since this paper is principally aimed at presenting DLF of RC slabs subjected to blat loads, different concrete slabs were modelled with a maximum unit of realistic dynamic load and consequently, before a static load was applied. The dynamic load is based on using SDOF models under triangular load (stage one). Then, by considering the maximum bending moments obtained from static and dynamic analyses, the dynamic coefficient (d) was derived for each structure by dividing the maximum of dynamic and static momentum of the slab (Eq. 7). Figure 8 shows the process of numerical analysis used in this study (Figure 8).

Numerical analysis
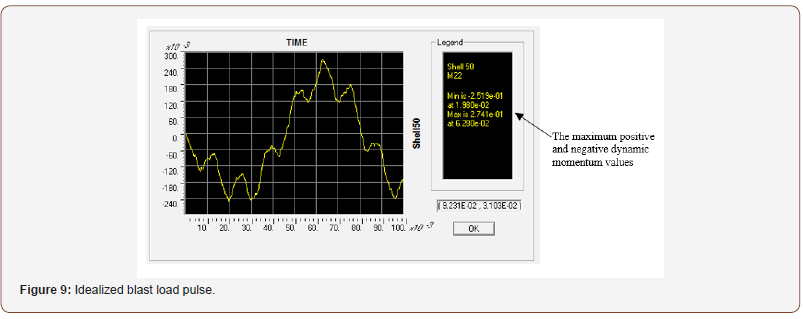
The behaviour of the thirty models (Table 1) was investigated numerically using the finite element software SAP2000, V 14 [29]. The RC slabs were modelled as shell elements having structural properties and boundary conditions equivalent to those of the physical models described in Table 2. The vibration period (T) of each slab was calculated and then the positive phase duration (td) is defined from the vibration period (T) and ratio of the member vibration (td/T). In the simulation of the slab response to the dynamic blast loading, as a record of pressure over time (pressuretime history) simulated by inputting the maximum unit load (F=1) in triangular shape (Figure 7) and the positive phase duration (td) of the slab from the first calculation the maximum forces are identified. Finally, the maximum positive and negative momentum of each slab defined (example shown on Figure 9). Figures 8 and 9 show examples of a dynamic and static analyses of a slab, which determined the maximum positive and negative momentum values, i.e. the equivalent loading response (Figures 9,10).
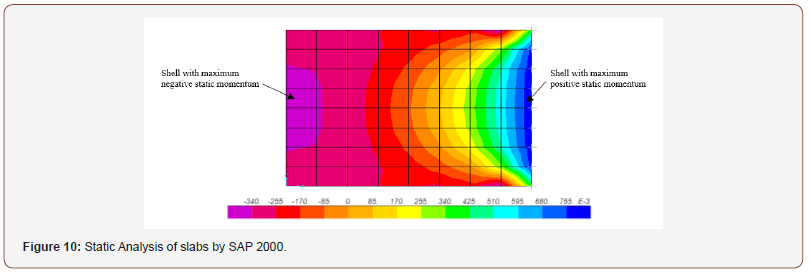
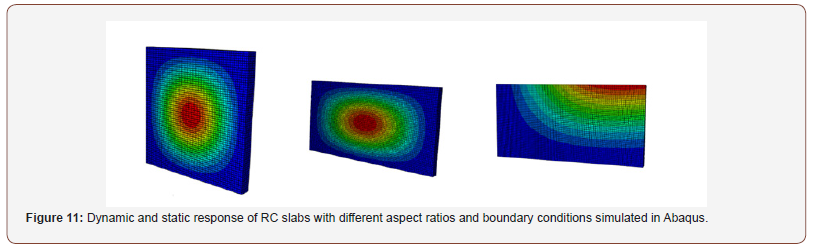
Three-dimensional (3D), non-linear dynamic analyses [30] were performed for all modelled RC slabs which were subjected to blast loads. These analyses were carried out in Abaqus and included modelling of both static and dynamic analysis using Abaqus/ Standard and Abaqus/Explicit respectively. The geometry of the analysed RC slabs was as shown on Figure 4, while the boundary conditions and different vibration periods were as defined in Section 2. The dynamic load with the overpressure peak of 100 kN and duration of 5 ms was applied and both dynamic load and static load of the same magnitude are applied to the RC slabs. In order to calculate the DLF, through numerical simulation, first a uniform dynamic load was applied through an explicit algorithm, before the uniform static load was applied to the RC slabs through an implicit algorithm. As explained before, the DLF are determined of the ratio of the dynamic deflection peak to the static deflection peak. The results were used to demonstrate the deformation of the slabs subject to above ground explosion (examples shown on Figure 10) and cover the responses of nonlinear calculated blast loads. The results of these analyses are compared to the equivalent loading response from SAP2000 (Figure 11). The comparative analysis will lead to a proposed method that can lead to more accurate and, therefore, more reliable predictions.
Model validation
In computer simulations, it is important to create validation models and select a simple case for which precise test data on the response behavior exists for verifiable loading conditions [31]. Since, to the best of our knowledge, there is no study on calculation of the dynamic force coefficient, a parametric study of the force coefficient based on the following calculations has been carried out to achieve same response of the slab under both dynamic displacement coefficient and dynamic force. Based on the general study of the dynamics of the structures presented below, if there is a vibration without damping in a Single Degree of Freedom (SDOF) system (i.e. no force), there should be a linear relationship between the displacement ratio and the internal force ratio of the members in a Multi-Degree of Freedom (MDOF) system (Figure 12).
Multi-degree-of-freedom (MDOF) computational approaches are generally similar to SDOF methods [5], but they include several masses, springs, and dampers. In MDOF systems, it is assumed that the total mass of a structure can be lumped into several representative floor masses and the stiffness can be illustrated by series of springs, as shown in Figure 11, Then, by applying the pulse force, all the masses, will displace in one direction with a certain velocity (Figure 13).
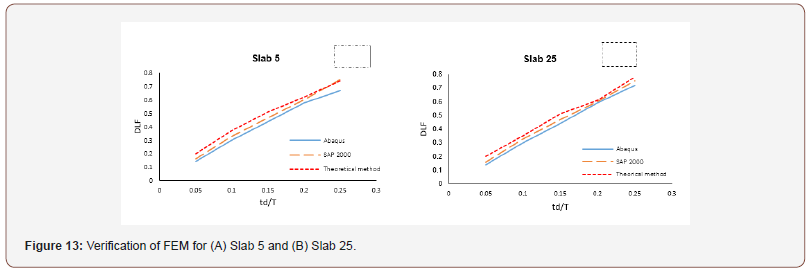
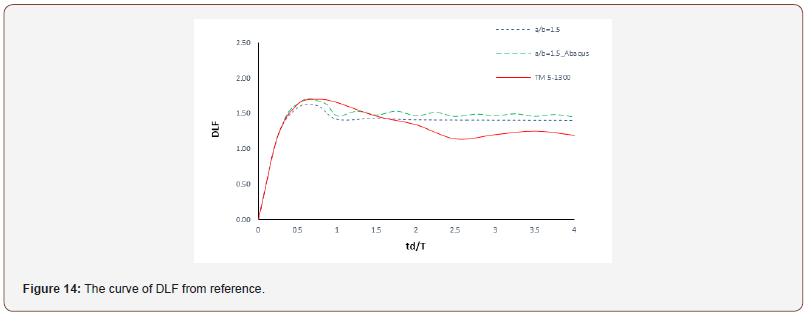
The results of the FEM analysis (SAP and Abaqus) and the theoretical analysis (MDOF) were used to demonstrate the capability of the model for reliable analysis of slabs. The comparative analysis showed that the results of the theoretical and FEM methods agree well with each other, and the results obtained by the two numerical methods are consistent. The analysis also showed that the values obtained with the FEM analysis are generally lower than the theoretical values. Nevertheless, Figure 12, shows that the results of the FEM analysis agree well with the theoretical method and the results obtained by the FEM analysis are consistent and robust enough to be adopted for further analysis. In order to ensure the accuracy of the results, the result of DLF from reference TM 5-1300 [10] (Figure 1) are used to demonstrate the capability of the models for reliable analysis of the RC slabs [32,33] (Figure 14).
It can be found that the results obtained from the two numerical methods are similar with the curve of DLF from reference. However, the values are higher for FEM analysis.
Analysis and Results
An example of the results from the numerical analyses are shown in Figure 13 for four different aspect ratios of an RC slab (include here the number corresponding to the modelled boundary condition shown in Table 1) (Figure 15).
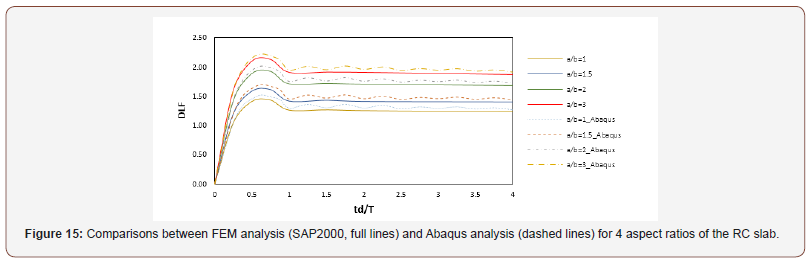
It can be observed that a good agreement in reaction timehistories, and the time for peak values occurrence exists. Moreover, the numerical results obtained for the different cases using both approaches show very good agreement in the value of the DLF. Figure 17 shows the comparison of the results of FEM numerical analysis (Abaqus) of 30 models of RC slabs (Table 1) for all four aspect rations modelled in this study (Figure 16).
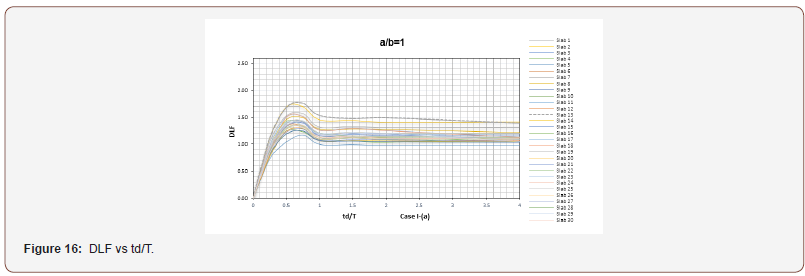
It can be observed that, in all cases, the modelled RC slab responses are within the same order of magnitude of d which, given that the peak of each graph lies 0.5 < td/T⩽ 1.0. The DLF increases in the period up to approximately td/T=0.65 and then it decreases in the period td/T= 0.65-1.0. Furthermore, it can be seen that DLF is relatively constant for td/T > 1, meaning that when a dynamic load is applied, the maximum dynamic momentum value is not greater than the static momentum values under the same amplitude of static load. However, it can also be seen that the results showed a variation trend of DLF for each slab and the response was governed by the different boundary conditions. Moreover, Slab 13 (two sides fixed, one side pinned and one side free boundary conditions) has the highest value for dynamic coefficient in most of the analysed cases (Figure 17).
In case І (a/b=1), the summary response graph illustrates that although different boundary conditions affected the values for DLF, the amplitude of the function has very little variation due to geometry. In case ІІ (a/b=1.5), it can clearly be seen that the highest values of d at slab 13 (insert boundary conditions), and in opposite the lowest values of the d at the slab 19 (with two sides pin and two sides free boundary conditions). As mentioned above, these can be explained through the different and contrasting boundary conditions. In cases ІIІ (a/b=2) and IIII (a/b=3), the maximum of the DLF develops at the slabs 13 and 18. However, it is observed that this trend is changed in case IIII due to different boundary conditions and different geometric ratios. It can be concluded that the value of DLF for each slab was affected by different ratios of vibration periods, different boundary conditions, and different geometric ratios (Figure 18).
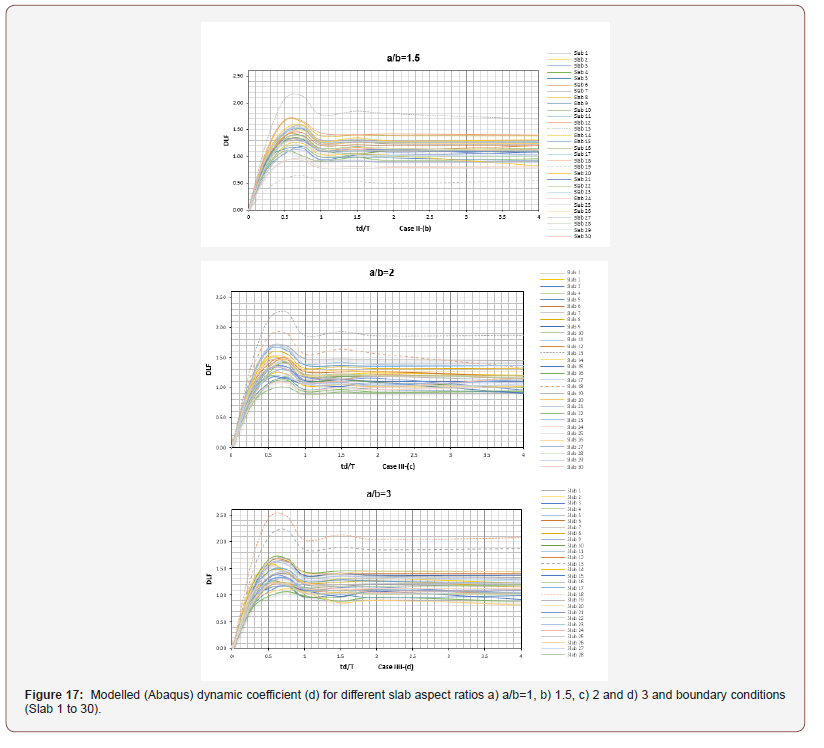
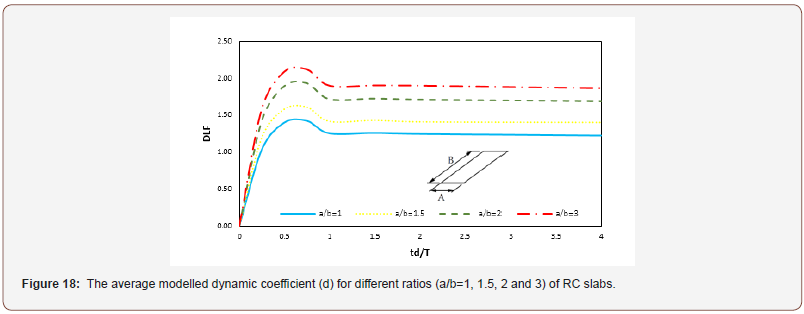

As discussed before, the results showed a variation trend of DLF for each slab and responses were governed by the respective of different ratios of vibration periods, different boundary conditions, and different geometric ratios. Furthermore, it can be seen that in each case of geometric ratios the amplitude of the function does not have change too much. Therefore, the response was assumed to be averaged into one graph for each case as it is shown in Figure 15. In addition, it can be concluded that the value of DLF increases with the increase in the aspect ratio
Conclusion
In this paper, numerical method was used to present the dynamic load factor (DLF) of concrete slabs with different ratios of vibration periods, different boundary conditions, and different geometric ratios. The RC slabs were modelled with different ratio of the length and the width 1, 1.5, 2 and 3 and smaller side is always constant 4 m, and the thickness for all slabs is 0.25 m. Slabs were reinforced by steel bars in both directions. RC slabs were analysed for seven different vibration periods of the member vibration (td/T) such as 0.25, 0.5, 0.75, 1.00, 1.50, 2.00 and 4.00. By considering different kind of the boundary condition, there were 30 models of RC slabs analysed in this study. It was found that the peak of each graph occurred at 0.5 < td/T⩽ 1.0 and it has also shown a variation trend of DLF for each slab. Furthermore, the response was governed by the respective of different conditions which presented in this paper. Overall, values of DLF are recommended for different conditions and it was found that when increasing the geometric ratios, the value of DLF also increases. The advantage of the proposed method is that leads to more precise, accurate, quick, and therefore reliable predictions.
Appendix A
This appendix shows the dynamic load factor (DLF) for Slab 1 to 30 (Figure 19).
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Kong X, Qi X, Gu Y, Lawan IA, Qu Y (2018) Numerical evaluation of blast resistance of RC slab strengthened with AFRP. Construction and Building Materials 178: 244–253.
- Choi JH, Choi SJ, Kim JHJ, Hong KN (2018) Evaluation of blast resistance and failure behavior of prestressed concrete under blast loading. Construction and Building Materials 173: 550–572.
- Stolz A, Fischer K, Roller C, Hauser S (2014) Dynamic bearing capacity of ductile concrete plates under blast loading. International Journal of Impact Engineering 69: 25-38.
- Cormie D, Mays G, Smith P (2012) Blast effects on buildings. 2nd ed. London: ICE Publishing.
- Krauthammer T, Astarlioglu S, Blasko J, Soh TB, Ng PH (2008) Pressure-Impulse Diagrams for Behavioral Assessment of Structural Components. International Journal of Structural Engineering 35(8): 771-783.
- Thiagarajan G, Kadambi AV, Robert S, Johnson CF (2015) Experimental and finite element analysis of doubly reinforced concrete slabs subjected to blast loads. International Journal of Impact Engineering 75: 162-173.
- Zhang B, Hailong C, Li M, Zheng Z, Zhou Y, et al. (2018) Equivalent static load method for hierarchical stiffened composite panel subjected to blast loading. Journal of Engineering Structures 171: 569–582.
- Wang W, Zhang D, Lu F, Wang SC, Tang F (2012) Experimental study on scaling the explosion resistance of a one-way square reinforced concrete slab under a close-in blast loading. International Journal of Impact Engineering 49: 158-164.
- TM 5-855-1 (1986) Fundamentals of Protective Design for Conventional Weapons, US Department of the Army, Washington DC, USA.
- TM 5-1300 (1990) The Design of Structures to Resist the Effects of Accidental Explosions, Technical Manual, US Department of the Army, Navy, and Air Force, Washington DC, USA.
- FEMA (2005) Risk Assessment: A How-To Guide to Mitigate Potential Terrorist Attacks, Risk Management Series, FEMA 452, Federal Emergency Management Agency, Washington DC, USA.
- API RP 753 (2007) Management of Hazards Associated with Location of Process Plant Portable Buildings, API Recommended Practice 753, First Edition, American Petroleum Institute, Washington DC, USA.
- Unified Facilities Criteria (UFC) (2008) Structures to Resist the Effects of Accidental Explosions, US Army Corps of Engineers, Naval Facilities Engineering Command, Air Force Civil Engineer Support Agency, UFC 3-340-02.
- ASCE (2010) Design of Blast-Resistant Buildings in Petrochemical Facilities (ASCE/Structural Engineering Institute (SEI) 59-11). American Society of Civil Engineers, Reston, VA, USA.
- ASCE (2011) Blast Protection of Buildings (ASCE/Structural Engineering Institute (SEI) 59-11). American Society of Civil Engineers, Reston, VA, USA.
- ACI (2014) Report for the Design of Concrete Structures for Blast Effects (ACI 370R-14) and Commentary. American Concrete Institute, Farmington Hills, MI, USA.
- Biggs JM (1964) Introduction to Structural Dynamics, McGraw-Hill, New York, USA, pp.341.
- Clough RW, Penzien J (1993) Dynamics of Structures, 2nd Edition, McGraw-Hill, New York, USA.
- Tedesco JW, Hayes J, Landis D (1987) Dynamic Response of Layered Structures Subject to Blast Effects of Non-Nuclear Weaponry. Computers & Structures 26(1-2): 79-86.
- Chopra AK (1980) Earthquake Dynamics of Structures, A Primer, Earthquake Engineering Research Institute, Oakland, CA.
- Dusenberry D (ed.) (2010) Handbook for Blast-Resistant Design of Buildings, John-Wiley & Sons, Inc, Hoboken, NJ.
- Micallef K, Sagaseta JV, Ruiz MF, Muttoni A (2014) Assessing punching shear failure in reinforced concrete flat slabs subjected to localized impact loading. International Journal of Impact Engineering 71: 17-33.
- Yilmaz T, Kirac N, Anil Ö, Erdem RT, Sezer C (2018) Low-velocity impact behaviour of two-way RC slab strengthening with CFRP strips. Construction and Building Materials 186: 1046–1063.
- Zhou XQ, Kuznetzov V, Hao H, Waschl J (2008) Numerical prediction of concrete slab response to blast loading. Int J Impact Eng 35(10): 1186-200.
- Yon J, Hawkins N, Koyayashi A (1991) Numerical Simulation of Mode I Dynamic Fracture of Concrete. Journal of Engineering Mechanics, ASCE 117(7): 1595-1609.
- Tedesco JW, Ross CA, Hughes M (1993) Load Rate Effects on Concrete Compressive Strength. Proceedings of the Sixth International Symposium on Interaction of Non-Nuclear Blasts with Structures 1: 194-199.
- Bhattacharyya A, Ravichandran G, Rittel D (2006) Strain Rate Effect on the Evolution of Deformation Texture for α-Fe. Metallurgical and Materials Transactions 37(4): 1137-1145.
- Smith PD, Hetherington JG (1994) Blast and Ballistic Loading of Structures, Butterworth-Heinemann Ltd., London, UK, pp.336.
- CSI, SAP2000, V14 (2009) Integrated Software for Structural Analysis and Design. Berkeley, CA, USA: Computer and Structures Inc (CSI).
- Abaqus Inc (2012) Abaqus User’s Manual – Standard Version 6.12. Abaqus Inc, Dassault Systèmes Simulia Corp. Providence, RI, USA.
- Krauthammer T, Jenssen A, Langseth M (1996) Precision Testing in Support of Computer Code Validation and Verification. Fortifikatorisk Notat Nr 234/96, Norwegian Defense Construction Service, Oslo, Norway.
- ACI (2011) Building Code Requirements for Structural Concrete (ACI 318-11) and Commentary. American Concrete Institute, Farmington Hills, MI, USA.
- Yan D, Lin G, Chen G (2009) Dynamic properties of plain concrete in triaxial stress state. ACI Mater J 106(1): 89-94.
-
Rohollah R, Slobodan B M, Nicholas H. Calculation of Dynamic Load Factor for Reinforced Concrete Slabs Subjected to Above Ground Explosion. Cur Trends Civil & Struct Eng. 5(2): 2020. CTCSE.MS.ID.000606.
-
Explosive loads, Dynamic load factor (DLF), Concrete slab, Sdof model, Vibration, Design, Building, Infrastructure, Blast resistance, Demonstrating
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






