Dealing with decision making is not trivial, nor does it involve purely rational aspects. Thus, the classical decision-making model based on the analysis of the decision-maker’s utility function and based on purely rational criteria of optimization seeking the best risk-return relationship, for example [1]. It can always be directly applied if we want to understand how decision-making takes place. The prospect theory Kahneman and De Tversky Y [2], of origin in psychology, can help us to understand a little more the mysteries involved in the decision-making process based on a paradigm other than the classic one [3].

Decision-making, in complex scenarios with often multiple goals, involves some judgment problems. In Keeney RL [4] view, evaluating trade-offs in the decision-making process is essential. Among the main ones cited by the author are not understanding the decision context, not measuring for consequences, or using inappropriate measures.

An exciting approach to be used in the decision-making process, also proposed by Kenney RL [5], is the possibility of using the context of complex decisions to try to find opportunities with the creation of smarter alternatives. The author draws a parallel between a classical model of decision-making based on other options and the model he proposes, the Value-Focused Thinking (VFT). VFT values become the drivers for the decision-making process. The implementation of the model requires more of the decision-maker since it is necessary to make the values explicit, think them previously to the other activities, and use them to identify opportunities in decision-making and the creation of alternatives. Such methodology seems to be very interesting for problems of the type that is discussed in this article. Because the choice of a triathlon race to be more appropriate, it is necessary to identify and explain its “values,” which can be here Understood as the strengths and weaknesses of athletes. Still, following the steps described by Kenney RL [5], for one to effectively use the VFT, it would be necessary for the decision-maker to seek to identify its objectives, structure them, create alternatives and analyze decision opportunities. A model capable of structuring the decision-making process of choice of tests, based on more rational criteria, considers models of optimization of results.

The AHP method is one of the multi-criteria decision analysis methods (MMAD). The use of such methods is particularly important for complex processes, especially in cases where multidisciplinary or complex issues are involved, which seek to prioritize existing alternatives to facilitate decision making. Although the multicriteria decision-making methods are part of the field of operational research (PO), they are framed in what is known as soft PO, insofar as it differs from PO hard because it is concerned with the correct definition and structuring of the problem [6].

The ability to investigate the essential aspects of the problem and its methodology makes the AHP method a prime decision-making process. Among the most important is the possibility of listing the best options and ordering the options by preference, based on the decisions of the decision-maker. It is worth emphasizing that the method deals well with subjective judgments, accepts both quantitative and qualitative data, ranks the options, and allows the verification of consistency in the process of choice.

For the use of AHP, one must structure the problem correctly. Without the correct structure of the problem, as previously discussed, it is not possible to apply the method successfully. Thus, for the proper application of this method, all various alternatives must be analyzed. This aspect is considered one of the most challenging and essential sections of the process. Once the problem is well structured, its solution is relatively simple.

The AHP method requires one to prepare a questionnaire in which the respondent is asked the importance of criterion “X” concerning criterion “Y.” For this, one must use the Basic Scale of Saaty TL [7], as can be established in Table 1.

As prescribed by Saaty TL [7], for the application of the method, it is necessary to compare the selected criteria, to be able to rank (rank) the alternatives. The result of this comparison will be the construction of square matrices, where the requirements can be compared and hierarchical to leave a subjective scale (verbal) for an objective scale (numerical), based on the aforementioned fundamental scale of Saaty TL [7]. Then, according to the author’s prescription, weights are calculated for each criterion based on its eigenvector, which should be normalized. In the sequence, the consistency index (CI), should be calculated for the consistency ratio (CR) estimation, as suggested by Saaty TL [8].

Previously, several sports articles used the AHP method. Sinuany Stern Z [9] used the technique to rank the Israeli league football team. Partovi FY and Corredoira RA [10] applied the model (AHP) along with other methods to analyze possible changes in soccer rules that could increase the attractiveness of the sport to the fans. Furthermore, studies applied this method with basketball and other sports [9, 11].

In reference to triathlon race selection, the athlete must identify the critical variables in the selection of the race. For example, a Brazilian athlete racing in February or March in the United States may have some advantage over their training due to seasonal differences. In Brazil, the triathlete experiences Summer through the months of December – March. However, the American triathlete experiences Winter during the same period. This season difference affects the ability of how each triathlete is able to train. Other important factors that a triathlete considers in race selection are, but not limited to, as follows:

1. Is the swim leg wetsuit legal?

2. Will the swim leg occur at sea, lake, or river?

3. Does the swim segment have a history of strong waves (i.e., IRONMAN© 70.3 Gulf Coast and IRONMAN Florida) or is it have a down-stream current (i.e., IRONMAN© 70.3 Chattanooga and IRONMAN© Chattanooga)?

4. Does the cycling course have steep climbs (i.e., IRONMAN© 70.3 Virginia Blue Ridge) or is has a history of strong winds (i.e., IRONMAN© 70.3 Gulf Coast and IRONMAN© Florida)?

5. Is the run course flat (i.e., IRONMAN© Maryland)?

6. When will the race occur? Will is occur in March or in November?

7. Does the athlete want to qualify for the IRONMAN© World Championships? Or is the event a “destination race?”

With this article, we explore several different race selection considerations such as: race location, climates, and seasonal/ environmental conditions for an IRONMAN© 70.3 event. This type of triathlon event features three immediate, consecutive events as follows: swimming, biking, and running. The length of each event is 1.9 kilometers, 90 kilometers, and 21.1 kilometers, respectively. The total distance of this type of triathlon event equals 70.3 miles, hence the name of this type of event (Figure 1).

The hierarchical structure shown in Figure 1 is of the descending type. The figure starts with the goal to be reached and ending with the possible alternatives, considering the weights established by the decision-maker for the various criteria.

The purpose of the decision-making process presented is to decide on what evidence a particular athlete should select, based on

their preference in terms of swimming, cycling, and running (which make up a triathlon event). The athlete should use the best suitable criteria for the swimming, cycling, and running stages. One should note that this is not the test that has such more natural steps, but preferably those that best fit the abilities of the athlete who is using the model. For example, if the competitor is an excellent swimmer, he can opt for tests where the swimming circuit is more challenging (more difficult), as this would have a relative advantage. The same rationale applies to the other disciplines of the triathlon test. The athlete constructs the matrix by the choices of the individual athlete and depends on the athlete’s aptitudes and preferences. The goal of the model is to give a more quantitative and rational aspect of the decision-making process.

For the analysis of the results, the the triathlete can use any software available capable in performing calculation. For this scenario, Microsoft Excel was used. After the hypothetical filling of the questionnaire, based on the scale suggested by Saaty TL [7], the vectors of priorities were generated (the treatment in the AHP model is of the matrix type). The results obtained are shown in Tables 2,3 below. For a detailed analysis of the assembly of the priority vectors and their weighting, in the light of the objectives it is recommended to consult the work of Saaty TL [7] (Table 2,3).

Table 1:Basic Scale of Saaty.

Table 2:Priority Vector.

Table 3:Priority vector in light of objectives.

The hypothetical athlete who filled the priority matrix used to make the priority vector (Table 2), has an excellent swimming ability. The IRONMAN© 70.3 Cozumel event has a swim in the open sea with strong currents. This event is more suitable to the athlete than an event with calm water, such as IRONMAN© 70.3 Lake Tahoe. Since cycling is not the athlete’s strength, especially in events with winds and climbs, the highest weight, at this stage, was with IRONMAN© 70.3 Lake Tahoe. As the athlete’s preference is for running in warmer places, the IRONMAN© 70.3s Cozumel and Saint Croix events are preferred. However, Cozumel is ranked first because of its flat terrain, while Saint Croix is second because of its hillier terrain.

As prescribed by Saaty TL [7], for the application of the method, it is necessary to compare the selected criteria, to be able to rank (rank) the alternatives. The result of this comparison will be the construction of square matrices, where the requirements can be compared and hierarchical to leave a subjective scale (verbal) for an objective scale (numerical), based on the aforementioned fundamental scale of Saaty TL [7]. Then, according to the author’s prescription, weights are calculated for each criterion based on its eigenvector, which should be normalized. In the sequence, the consistency index (CI), should be calculated for the consistency ratio (CR) estimation, as suggested by Saaty TL [8].

The matrix analysis generated by the decision maker’s answers can be considered consistent, since, as prescribed by Saaty TL [7], the consistency ratio was lower than 0.05, which is a very reasonable value, depending on the number of criteria (N). For this, it is necessary to find the consistency index - IC, where n represents the order of the matrix, and 𝝀max indicates the largest eigenvalue of the matrix.

The calculation of the consistency index can be done with the support of the following formula:

Equation 1:

CI=(λmax-n)/(n-1)

λmax=ci

After calculating the CI, the athlete can calculate the consistency ratio (CR) should. The CI is the consistency index, and RI is the random index, proposed by Saaty (1980), as a function of the order of the matrix, as can be seen in below (Table 4).

Equation 2:

CR=CI/RI

The inconsistency observed in the normalized vector of the swimming criterion was 0.03, in the cycling criterion it was 0.01, and in the race, the criterion was 0.08. As the established standard for acceptance is usually up to 10% (or 0.1), one can consider the values obtained within the expected, so that the model can be applied to this data matrix (choices).

Based on the information in Table 3,4 and with the help of the software expert choice 11.5, it was possible to find the overall priority of a hypothetical athlete, considering their ability and preferences in terms of the type of test and conditions General (climatic and relevant, for example). For this, the hypothetical athlete used the aggregation function proposed by Saaty TL [7]. The results indicated that the best alternative for the athlete in question would be to consider Cozumel as the first with Saint Croix as a second option and Lake Tahoe as the third option, as shown in Table 5. The results in Table 5 are in percentage form, so Cozumel is 61.80%, Saint Croix is 27.80%, and Lake Tahoe is 10.40%. In this case, there was a significant discrimination between the three pre-selected tests. Of course, a first step would be a pre-selection, with the sole purpose of reducing the number of variables to be analyzed. This pre-selection could take into account the planning of the athlete’s periodization, the logistics of the race, or any other relevant aspect (Table 5).

Table 4:Random Consistency Index.

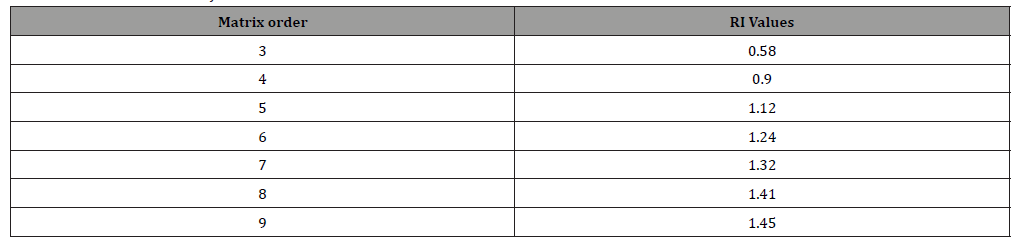
Table 5:Global Priority Vector (GPV).

The purpose of this article was to demonstrate the use of a multicriteria decision model to aid in the decision-making process for the triathlon choice. Such a model can be applied, in different ways, in other sports modalities. The essential aspect of any decision-making process is to use objectivity, with the help of tools that support the decision-making process. Therefore, it is a matter of trying to quantify aspects inherent to the decisionmaking process that would otherwise remain in the subjectivity field. The main objective of the technique is to work quantitatively (objectively), with variables that would be subjective, if no method were used to aid in the decision process. One point that may be the subject of future study is pondering, with higher weight, the cycling stage since it is the longest stage of a triathlon race.

None.

No conflict of interest.

1. Von neumann Je, Morgenstern O (1944) Theory of games and Economic Behavior. Princeton University Press, USA, pp: 776.
2. Kahneman, De Tversky Y (1979) Prospect Theory: Na Analyses of Decisions under Risk. Econometrica 47(2): 262-291.
3. Zank H (2001) Cumulative Prospect Theory for Parametric and Multiatribute Utilities. Mathematics of Operations Research 26(1): 67-81.
4. Keeney RL (2002) Common Mistakes in Making Value Trade-Offs. Operations Research 50(6): 935-945.
5. Keeney RL (1996) Value-Focused Thinking: Identifying Decision Opportunities and Creating Alternatives. European Journal of Operational Research 92(3): 537-549.
6. Ensslin SR, Ensslin L, Dutra A, Igarashi DCC (2005) Hard View or Soft View of Operations Research? Reflections on Postures and Procedures. Brazil.
7. Saaty TL (1980) The Analytic Hierarchy Process. Quantitative Assessment in Arms Control, McGraw-Hill, USA, pp: 285-308.
8. Saaty TL (1977) A Scaling Methods for Priorities in Hierarchical Structures. Journal of Mathematical Psychology 15(3): 234-281.
9. Sinuany stern Z, Israel Y, Bareli M (2006) Application of the analytic hierarchy process for the evaluation of basketball teams. International Journal of Sport Management and Marketing 1(3): 193-207.
10. Partovi FY, Corredoira RA (2002) Quality function deployment for the good of soccer. European Journal of Operational Research 137(3): 642-656
11. Sinuany stern Z (1988) Ranking of Sports Teams via the AHP. The Journal of the Operational Research Society 39(7): 661-667.