Sample size calculations are a waste of time, money and energy and should be replaced by sample size considerations

Before performing a medical study, it is necessary to determine the number of subjects to be included in the study. This is mostly done by performing a sample size calculation. A sample size calculation is assumed to be so important, that a sample size calculation has to be added to all application forms for grants for medical research. Medical ethics committees only give permission for a study to be performed if the researcher can provide an appropriate sample size calculation. In addition, the so-called CONSORT statement, a statement that specifies the guidelines of a scientific paper reporting the results of a randomized controlled trial (RCT), state that a sample size calculation must be included in the paper. Because all major medical journals (New England Journal of Medicine, JAMA, Lancet, British Medical Journal, etc.) endorse this CONSORT statement, it is more or less mandatory to include a sample size calculation in the scientific paper reporting the results of an RCT.

Sample size calculations were initially set up to determine the size of a study population in an RCT. The idea of a sample size calculation is to calculate how many subjects should be included in both the intervention group and the control group to make a predefined difference between the two groups (i.e. a predefined effect) statistically significant. It should be realized that sample size calculations are fully based on testing theory. So, they are based on the dichotomization of the existence of a certain effect in medical research. Besides the fact that such a dichotomy does not exist [1- 6], the decision whether there is an effect or not is also based on an arbitrary cut-off value. Furthermore, in the equation to calculate the sample size some more or less arbitrary numbers must be entered to obtain the final sample size.

For sample size calculations, many online tools are available. However, a sample size calculation is basically very simple and can be easily calculated by hand. Equation 1 shows, for instance, the equation to calculate the sample size for an RCT with two groups with the same number of subjects in both groups, and with a continuous outcome variable.

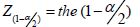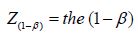where n₁=n₂= the sample size in either the intervention or control group, percentile point of the standard normal distribution, percentile point of the standard normal distribution, σ = the standard deviation of the outcome variable and 𝝊 = the predefined effect (i.e. the predefined difference in mean value of the outcome variable between the groups).

The first part of the equation involves testing theory in which α reflects the significance level and (1−β ) reflects the power of the statistical test. Furthermore, the standard deviation (σ) and the predefined effect (𝝊) must be entered into the equation. It should be realized that only the significance level (although it is basically an arbitrary value) is more or less fixed at 0.05. All other parameters are relatively flexible. For the power of the study, for instance, either 0.90 or 0.80 can be chosen. Furthermore, the standard deviation that is going to be found in the study is, of course, not known. To get a proxy of the standard deviation sometimes a pilot study is performed or sometimes the expected standard deviation is obtained from the literature. Also, the predefined effect that has to be statistically significant is not fixed. So, there is some flexibility in choosing the numbers that are entered into the equation. It is striking to see the consequences of this flexibility in the calculated sample size. Consider an RCT in which the effect of a new medication for blood pressure reduction is investigated. Table 1 shows the effect of the flexibility in choosing the numbers entered into the equation on the calculated sample size. It should be realized that in the example all the numbers used to calculate the sample sizes are acceptable and realistic.

Table 1: Consequences of the flexibility in choosing the numbers used for the sample size calculation

The results of the example show that within the range of acceptable numbers, the calculated sample size can vary between 526 and 62 patients per group (so between 1052 and 124 in total). The good news is that, as long as the numbers that are used in the sample size calculation make sense, all sample size calculations are acceptable for grant providers, for medical ethical committees and for scientific journals. So, because a sample size calculation is based on more or less arbitrary numbers, which makes that the result of a sample size calculation can be almost everything, it does not provide any interesting information [7-9].

Another problem with sample size calculations is that they are mostly used in the wrong way. Because there is a lot of flexibility in the numbers used in the sample size calculation, researchers do not start by thinking about the power of the study, the expected standard deviation and the effect that has to be statistically significant. They often start with the maximum number of subjects that can be included in a certain study. The other three flexible parameters (power, standard deviation and predefined effect) are changed in such a way that the number of subjects calculated is slightly lower than the maximum number of subjects that can be included. Slightly lower, because then also some drop-outs can be added to the required sample size.

Although sample size calculations do not provide any interesting information, surprisingly, sample size calculations seem to become more and more important. Seminars and courses are given highlighting the importance of performing a sample size calculation. Papers are written with sample size calculations for all kinds of research situations. A narrative search in the National Library of Medicine on sample size calculations gave more than 17,000 results in total, with almost 1,500 results in the last year. The mostly used argument for performing a sample size calculation is that if a sample size is too small, one will not be able to detect an effect, while if a sample size is too large, it may be a waste of time and money [10]. The argument not be able to detect an effect is a misunderstanding which is caused by a misunderstanding about statistical significance and a strong believe in the importance of using an arbitrary cut-off value for deciding whether an effect is present or not. A statement based on the misunderstanding that a non-statistically significant effect indicates that there is no effect [1-6]. The argument that if a sample size is too large, there is a possible waste of time and money is a bit shortsighted. A result of a calculation does not give an answer to the question whether there is possible waste of time and money. It is important to realize that not using a sample size calculation, does not mean that researchers should not think about the sample size anymore before performing a study. That is definitely of utmost importance. However, thinking about the sample size is not the same as calculating a sample size. Suppose, for instance, that a study is performed to investigate the difference in quality of life between elderly subjects living in urban and rural areas. Quality of life is measured with an online questionnaire that takes about 5 minutes to fill in. Suppose that for this study a sample size calculation was performed showing that 200 subjects are needed in both areas to get a certain predefined difference in quality of life statistically significant. In this situation, it does not make sense to use a sample size of only 200 subjects. Much more subjects should be asked to fill in the questionnaire, leading to huge sample size and therefore, a very efficient estimate of the difference in quality of life between elderly subjects living in urban and rural areas. On the other side of the spectrum, suppose a study is performed in child care to investigate the effect of a new medication for a certain child disease. The disease it not very common, so it is very difficult to include many children with that particular disease. Suppose, a sample size calculation indicated that 100 children are needed in both the intervention and the control group to get a certain predefined effect of the medication statistically significant. Suppose further that, to include 100 children, it takes more than 15 years of inclusion. So, based on sample size calculation theory, a study like this can never be performed, which is a terrible decision. In this case, the study should be performed with less patients, probably resulting in a non-significant effect estimate. However, a study like this can still provide important information about the clinical relevance of the new medication. Especially in an era in which evidence-based medicine is mostly driven by the results of meta-analyses [11,12]. Basically, when the sample size for a particular study has to be determined, there is only one solution. The sample size must be as big as possible! Because the bigger the sample size, the more efficient the effect estimate will be. As big as possible not based on the number obtained from a sample size calculation, but based on other considerations, such as financial, logistical and ethical ones. Only by using those arguments, it can be determined whether a certain large sample size is a waste of time and money.

Because sample size calculations are totally based on testing theory with a non-existing dichotomy, because changing the numbers entered into the equation within reasonable ranges lead to totally different sample sizes and because sample size calculations are often used in a wrong way, it is highly advised not to use sample size calculations anymore. Nevertheless, it is still very important to think about the sample size before performing a medical study, but this should better be based on financial, logistical and ethical considerations. In light of this, sample size calculations should be changed into sample size considerations.

None.

None.

significance tests? BMJ 322: 266-231.
1. Greenland S, Senn SJ, Rothman KJ, Carlin JB, Poole C, et al. (2016) Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. European Journal of Epidemiology 31(4): 337-350.
2. Amrhein V, Greenland S, McShane B (2019) Retire statistical significance. Nature 567: 305-307.
3. McShane BB, Gal D, Gelman A, Robert C, Tackett JL (2019) Abandon Statistical Significance. The American Statistician 73(sup1): 235-245.
4. Wasserstein RL, Schirm AL, Lazar NA (2019) Moving to a World Beyond “p < 0.05”. The American Statistician 73(sup1): 1-19.
5. Twisk JWR (2024) Refrain from statistical testing in medical research; it does more harm than good. Annals of Public

Health & Epidemiology 2 :3.

6. Bland JM (2009) The tyranny of power: Is there a better way to calculate sample size. BMJ 339: b3895.
7. Schulz KF, Grimes DA (2005) Epidemiology 1 - Sample size calculations in randomized trials: mandatory and mystical. Lancet 365(9467): 1348-1353.
8. Bacchetti P (2010) Current sample size conventions: Flaws, harms, and alternatives. BMC Medicine 8: 17.
9. Noordzij M, Dekker FW, Zoccali C, Jager KJ (2011) Sample size calculations. Nephron Clinical Practice 118: c319-c323.
10. Edwards SJL, Lilford RJ, Braunholtz D, Jackson J (1997) Why “underpowered” trials are not necessarily unethical. Lancet 350(9080): 804-807.
11. Guyatt GH, Mills EJ, Elbourne D (2008) In the era of systematic reviews, does the size of an individual trial still matter? PLoS Medicine 5(1): e4.