Seismic Signal Processing in Some Wave Propagation Problems Through Dynamical Condensation Approach

On the 28 December 2022 press group 24 hours (24 Hours-168 Histories) warned that a catastrophic earthquake is coming in the Balkans: https://www.24chasa.bg/articla/13797525

On December 28, 2022, Associate Professor Philip Philipoff shared with “24 hours-168 stories” that the Balkans has accumulated huge seismic potential. After a weekrealized an earthquake on the island of Crete with a magnitude of M=5.7 In a month and a week, on February 6, 2023, they will be realized the pair of earthquakes- twins in the Karamanmarash region with magnitudes M=7.7 and M=7.6. Such a phenomenon with a pair of twin epicenters realized once in 500 years. The study is summarized previous publications of the authors: [1-11] and the results of the other authors [12, 13]. Some people sense the dangers-this is inherited from animals. The dog, which has descended from the wolf by domestication, has the keenest sense of danger in the living world. Ten days before the disaster in Fukushima, a large group of Bulgarian scientists felt a sense of danger and tried to get help from the then Bulgarian government [6]. On March 11, 2011, the Japanese managed to withdraw the nuclear fuel from the Fukushima plant. If a parallel plant had been switched on within 10 minutes (seconds) and the temperature drop had started immediately, the disaster could have been avoided

Main Results and Discussions

Seven frequency domain theorems proofed by the authors [3, 4, 8] are presented in the paper as follows:

• Theorem 1: (The phenomenon “Symmetry” in the time domain corresponds to the phenomenon “Conjugation” in the frequency domain). The complex Fourier F(jω) spectra of the symmetric real functions in the first and second quadrants are conjugated as well as.

• Theorem 2: The complex Fourier F(jω) spectra of the symmetric real functions in the third and fourth quadrants are conjugated respectively.

• Theorem 3: (The phenomenon “Anti Symmetry” in the time domain corresponds to the phenomenon “Anti Conjugation” in the frequency domain). The complex Fourier F(jω) spectra of the anti symmetric real functions in the first and third quadrant are anti conjugated as well as.

• Theorem 4: The amplitudes of the functions in first and second quadrants are both positive, while these of the amplitudes for the functions for third and four quadrants are both negative. The functions under investigation could be of arbitrary amplitudes-negative or positive. The corresponding complex Fourier F(jω) spectra also are of arbitrary type amplitudes-negative or positive.

• Theorem 5: (Frequency indistinguishable). Four quadruple symmetric real functions are frequency indistinguishable.

• Theorem 6: (The phenomenon “Symmetry” in the time domain corresponds to the phenomenon “Conjugation” in the frequency domain. The phenomenon “Anti Symmetry” in the time domain corresponds to the phenomenon “Anti Conjugation” in the frequency domain. The simultaneous operation of the Theorems 1 and 3 leads to even and odd decomposition of the Fourier complex spectrum of the common function F _{communication}with length N in the time domain. This result represents spectral function, composed by the equivalent nonzero real and imaginary spectral parts with length N/2 in the frequency domain( ω) and as follows:

• Theorem 7: Of all the displacements satisfying the kinematic graphic conditions, a stationary (extreme) conception of the potential energy communicates precisely those displacements that satisfy the equilibrium equations of the task. an important requirement of the cited potential energy theorem is that the unknown required displacements of the problem must satisfy the given values of the boundary displacements and From here it immediately follows that the INDESTRUCTIBILITY of the nodes of the neural network is guaranteed if the total VELOCITIES in the direction of movement of the inertial motors caused by the external influences and the controlling influences are equal to ZERO The theorem is proved.

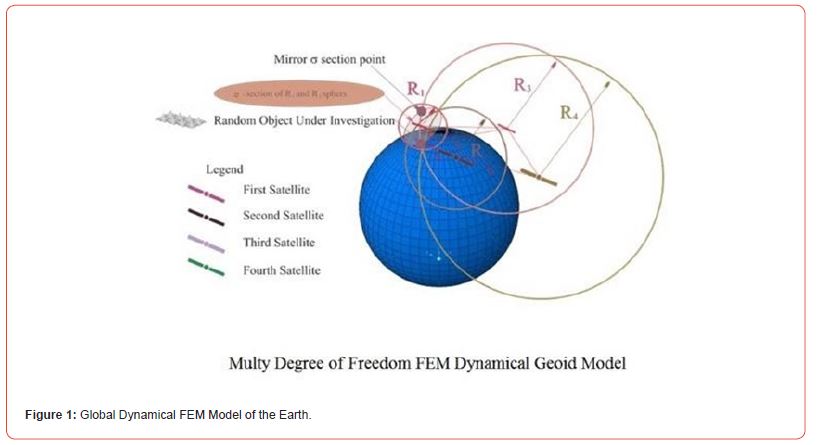
Theorem 6 for example, can be interpreted as an analog variant of the James Cooley and John Tuckey FFT scheme [14]. Here is Fourier complex spectrum with length N in the time domain are imaginary spectral parts with length N/2 in the frequency domain. A dynamic Geoid model is developed with a very large number of dynamic degrees of freedom. Master and Slave variables are introduced.

A condensed description is constructed using the dynamic condensation method. It involves the Master degrees of freedom as variables. Slave variables are condensed and participate implicitly in a condensed description. Condensation is performed according to the Gaussian algorithm. The condensed description explicitly contains only the Master degrees of freedom, but has the accuracy of the initial description. In the condensed description, boundary conditions and loads with external effects in the direction of the Slave degrees of freedom are implicitly accounted for by participating in the condensed equations. This makes it possible to account for all degrees of freedom and all external influences in the final solution. The condensed finite element model, for example, is implemented on a real-time supercomputer. Future local (certain region) or global (whole Earth) seismic activity with all degrees of freedom in the condensed description is estimated. As a result, a prospective estimate of the global seismic activity forward in time is obtained. The condensed description is on that 20% of the planet Earth on which there is seismic activity. The remaining degrees of freedom are not lost, but are accounted for implicitly. As a result, coordinates, frequency composition, duration of seismic signals (for example, velocities) along the direction of the Master variables are obtained. Destructibility conditions are formulated according to the mechanics of destruction, and areas of failure are marked in which there is a risk of destruction with casualties. These results are compared with experimentally obtained real- time measurements from GNSS.

Figures 1-4

The report proposes a hybrid dynamic model based on the finite element method with a large number of dynamic degrees of freedom in combination with a GNSS system. The method of dynamic condensation is used. The Bulgarian version of this method is based on the protected three dissertations 1) Dineva, P, (1986) “Dampening and control of the movement of structures under seismic impacts”, 2) Philipoff, Ph (1987), “Modeling of systems “environment-structure” under seismic impacts”, Ph.D. Dissertation, Institute of Mechanics-BAS, Sofia, Bulgaria, 1987,3) Ishtev, K (2002), “Models and management of construction facilities under seismic impacts” , Dissertation “Doctor of Technical Sciences”, 2002. It involves the Master degrees of freedom as variables. Slave variables are condensed and participate implicitly in a condensed description. Condensation is performed according to the Gaussian algorithm. The condensed description explicitly contains only the Master degrees of freedom, but has the accuracy of the initial description.

In the condensed description, boundary conditions and loads with external effects in the direction of the Slave degrees of freedom are implicitly accounted for by participating in the condensed equations. This makes it possible to account for all degrees of freedom and all external influences in the final solution. The condensed finite element model, for example, is implemented on a real-time supercomputer. Numerical results are combined with real-time GNSS measurements. Numerical results are combined with real- time GNSS measurements. The model can be useful in earthquake prediction.

The authors express their gratitude to administrative management of TU Sofia, Kondov & Kaliqi Design Team, administrative management of UASG and GPS Control EAD for their support in the development of this study.

None.

1. Philipoff Ph, Ph Michaylov, (2007) BELENE Nuclear Power Plant Numerical and Experimental Bedrock. Layers and Surface Signals, J Applied Mathematical Modeling Elsevier31(9): 1889-1898.
2. Maya Kurteva, Philip Philipoff, Dimitar Dimitrov (2009) Assessment of Some Elements of Environmental Risk Factors in the Bulgarian Mountains. Comptes rendus de l’Acad´ emie bulgare des Sciences Tome 62 343: 745-752.
3. Philipoff Ph, D. Demirev, A. Yusuf, M Islam, D Stankov, et al (2010) Some Psychology and Technical Aspects of a Rescue Operation in the Musala Peak Region (Rila Mountain). Procedia Social and Behavioral Sciences Elsevier WCPCG (5): 384-391.
4. Jivkov Venelin, Philip Philipoff, Anastas Ivanov, Mario Muсoz, Galerida Raikova, Mikhail Tatur, et al (2013) Spectral properties of quadruple symmetric real functions. Applied Mathematics and Computation-Elsevier 221:344-350
5. Jivkov V, Natarajan V, Paneva A, Philipoff P (2017) Forecasting of Strong Earthquakes M>6 According to Energy Approach. J Earth Sci Clim Change 8(12).
6. Venelin Zhivkov, Filip Filipov, Rumyana Bozhinova, Yordan Tankovski, Petar Getsov, et al. (2017) Some Models of Behavior in Tasks for Risk Management of Natural Disasters Transport Accidents and Industrial Accidents Transport Accidents and Industrial Accidents. Conference: Psychology-Theory and Practice pp 6-7.
7. Venkatanathan Natarajan, Philip Philipoff (2018) Observation of surface and atmospheric parameters using NOAA 18 satellite: a study on earthquakes of Sumatra and Nicobar Is regions for the year 2014 (M>6.0). Natural Hazards Volume 92(2).
8. Filip Filipov (2023) National neural network for seismic protection and wind protection of buildings and facilities. Mechanics Days Varna.
9. Venelin Kondov, Diana Bankova (2023) Seismic Risk Management Part 1 and 2 Days of Mechanics. Varna.
10. Petya Minkova (2024) 20 days ahead with satellite data and supercomputers. Catastrophic earthquakes can be predicted 20 days ahead with satellite data and supercomputers.
11. Seismic, Wind and Fire Protection of Buildings and Facilities Through Renovation of Existing Elevator Devices. Input number № ВХ-113973/10.10.2024, Patent Office of Republic of Bulgaria.
12. Tsanovski Y (2015) Lecture course on Global Navigation and Satellite Systems and Networks. University of Architecture Civil Engineering and Geodesy Sofia.
13. Tsanovski Y (2016/2017) Lecture Course on Precision GPS Measurements. University of Architecture Civil Engineering and Geodesy Sofia.
14. AD Poularikas (2000) The Handbook of Formulas and Tables for Signal Processing, CRC Press LLC. Springer Verlag Boca Raton FL New York (in English).