Nonlinear Partial Differential Equations Analysis in all Engineering Fields (Chemical, Mechanical, Civil, Electrical and other fields) and Basic Sciences by new Approach ASM

Partial nonlinear differential equations which arise in real- world physical problems are often too complicated to be solved exactly [1,2]. And even if an exact solution is obtainable, the required calculations may be too complicated to be practical, or it might be difficult to interpret the outcome. In fact, solving nonlinear equations can guide researchers to comprehend the physical phenomena deeply and sometimes leads them to investigate some facts which are not easily understood through common observations [3,4]. Based on the above explanations, here we aim to discuss nonlinear partial differential and the behavior of the physical its. In this literature, we have a governing equation for studying nonlinear behavior in engineering processes and solving it analytically with a new approach like AGM, Akbari Ganji Method [5-10]. This method is called the abbreviation ASM (Akbari Sara’s Method), which can easily solve all nonlinear problems in case analytical and is very simple and flexible. Other methods [11] compared to ASM do not have this ability to gain the solution of the presented problem in high precision and accuracy so nonlinear differential equations such as the presented problem in this case study should be solved by utilizing new approaches.

We consider an unsteady state of nonlinear partial differential equation with constant physical coefficients that depends on the engineering process. The constant values 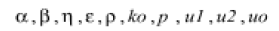depend on what field of engineering we want to solve this equation. For example, these constant values in mass transfer, heat and fluid transfer, electrical circuits, as well as in beam-column equations are defined respectively in chemical engineering, mechanical engineering, civil engineering and electrical engineering and all engineering fields.

The governing nonlinear partial differential equation of engineering fields is expressed as follows:

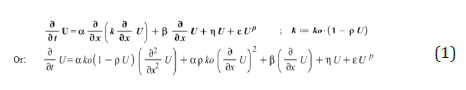
Boundary and initial condition:

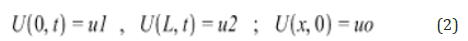
We separate equation Eq. (1) from steady and unsteady state as follows:

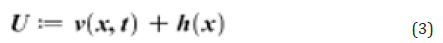
After separation, the result is given by the following two differential equations:

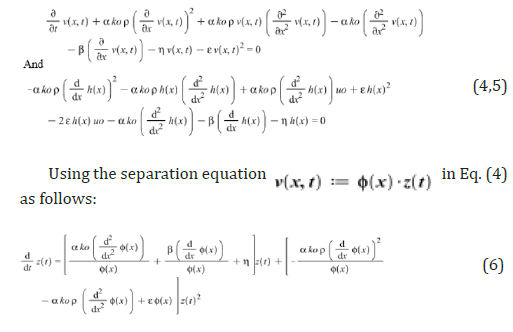
The coefficient z(t) in the Eq. (6) can derive the following differential equation for calculating eigenvalues λ and its function

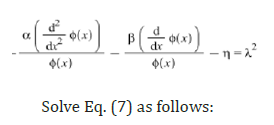
And boundary conditions:

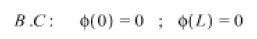
The constant coefficients _C1, C2 are obtained from Eq. (8) and given the homogeneous boundary condition with forming the coefficients matrix for the homogeneous equation as follow:

The parameters of Eq. (10) are as follows:

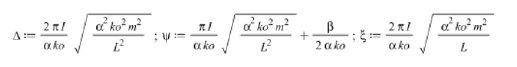
By selecting the physical values as follows:

Using the orthogonality of the modes of the function φ(x) in Eq. (6), we can obtain the following:

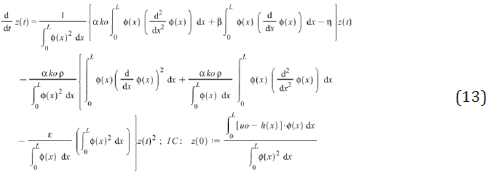
After substituted the physical values Eqs. (12) and the eigenvalue function Eqs. (10,11), and solving it by ASM method Eq. (13), the following is obtained:

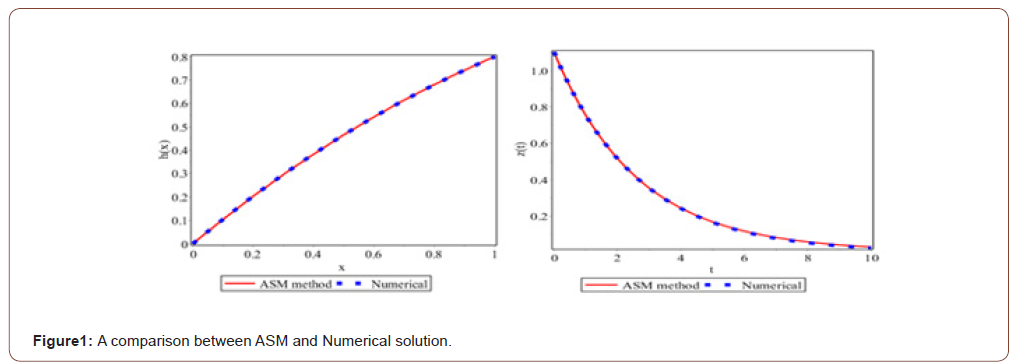
(Figure 1) And finally the solution of the nonlinear partial differential Eq. (1) is solved analytically by ASM method as follow:

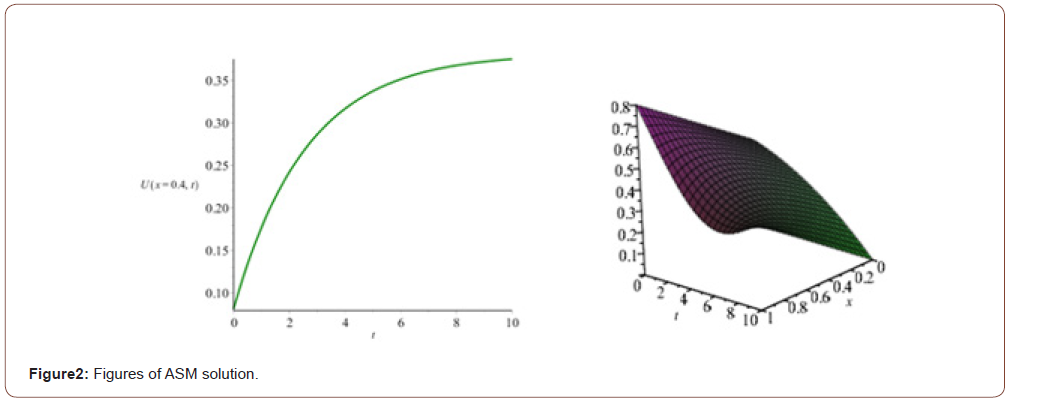
The diagram of the place-time is as follows: (Figure 2)

In this paper, one complicated nonlinear partial differential equation has been introduced and analyzed completely by Akbari- Sara’s Method (ASM) and also the obtained results have been compared with Numerical Method (Runge-Kutte 4th). A modern method (ASM) for solving all kinds of complicate nonlinear partial differential equations in engineer field and basic science which can be PDEs, or ODEs has been presented.

ASM and AGM (Akbari Sara’s Method and Akbari-Ganji Methods) have been invented mainly by Mohammadreza Akbari (MR Akbari) in 2019 and 2014 respectively in order to provide a good service for researchers who are a pioneer in the field of nonlinear differential equations. It is worthy to note that I am really grateful to all those who encouraged me to devise these methods which are highly beneficial for analytical solving coupled nonlinear ODEs (especially ASM) in Engineering, basic Sciences and Economic.

No conflicts of interest.

1. Zhilum Xu (1992) Applied Elasticity. Wiley Estern limited.
2. JK Zhou (1986) Differential Transformation and its Applications for Electrical Circuits. Huazhong Univ Press Wuhan China.
3. DD Ganji (2006) The application of He’s homotopy perturbation method to nonlinear equations arising in heat transfer. Phys Lett A 355(4-5): 337-341.
4. JH He (1999) Homotopy perturbation technique. J Comput Methods Appl Mech Engrg 17(8): 257-262.
5. MR Akbari, DD Ganji M Nimafar (2014) Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach. Frontiers of Mechanical Engineering Journal
6. K Rostami, MR Akbari, DD Ganji, S Heydari (2014) Investigating Jeffery-Hamel flow with high magnetic field and nanoparticle by HPM and AGM. Cent Eur J Eng 4(4): 357-370.
7. MR Akbari, DD Ganji, A Majidian, AR Ahmadi (2014) Solving nonlinear differential equations of Vanderpol, Rayleigh and Duffing by AGM. Frontiers of Mechanical Engineering.
8. DD Ganji, MR Akbari, AR Goltabar (2014) Dynamic Vibration Analysis for Non-linear Partial Differential Equation of the Beam - columns with Shear Deformation and Rotary Inertia by AGM. Development and Applications of Oceanic Engineering (DAOE).
9. MR Akbari, DD Ganji, AR Ahmadi, Sayyid H Hashemi kachapi (2014) Analyzing the Nonlinear Vibrational wave differential equation for the simplified model of Tower Cranes by (AGM). Frontiers of Mechanical Engineering 9(1): 58-70.
10. MR Akbari, M Nimafar, DD Ganji, MM Akbarzade (2014) Scrutiny of non-linear differential equations Euler Bernoulli beam with large rotational deviation by AGM. Springer.
11. JH He (1998) Approximate solution for nonlinear differential equations with convolution product nonlinearities. Comput Math Appl Mech Eng 167(1-2): 69-73.