 Mini Review
Mini Review
Mathematical Modeling of Covid-19 Spread
Patrice F Dassonville*
Department of Biomedical sciences, Freelance researcher, France
Patrice F Dassonville, Department of Biomedical sciences, Freelance researcher, France.
Received Date: October 12, 2020; Published Date: November 06, 2020
Abstract
The expand of the virus observed through a mathematical modeling.
Keywords: Erratic; Exponential; Multidisciplinarity; Spread Index
Introduction
It is not about saying how to cure the disease, but about making behaviors more effective in facing the way the virus expands. The mathematical modeling raises awareness of the seriousness of the problem, thanks to a complementary approach. Once again it emphasizes the effectiveness of multidisciplinary. The spread of the virus deserves a detailed analysis, especially in regard to the actual threat of a serious blowback. It can be described with a three-dimentional statistical model: exponential, erratic and cumulative. However, time is not a phenomenon and space have no materiality [1], the two concepts will help understanding the topic.
Origins and Purpose of Mathematical Modeling
Mathematics does not exist in nature; in fact, it is an operating mode of thought which is intended to simplify problem solving. The following examples explain why mathematics had to be invented:
• Small ceramics called Calculi (Iraqi Kurdistan, c. 5000 BCE) were intended to keep accounts [[2], p. 49]. It is no doubt the onset of business administration and management.
• According to the Greek geographer Strabo (c. 61 BCE-c. 22 CE) arithmetic was created by Phoenician sailors for their trade accounts with all countries around Mediterranean Sea [3]. They also invented the linear consonantal alphabet c. 11th century BCE [2, p. 190].
• Geometry was invented by Sumerians and Egyptians for their huge monuments like the stone step pyramid designed by the architect Imhotep for pharaoh Djoser (Saqqarah c. 2700 BCE) [[4], p. 84].
The purpose of mathematical modeling is to provide an angle of view as complementary as effective for description and evaluation of physical phenomena, of architectural projects, of financial policy, of demographic statistics, etc.
The Spread Modeling
The effectiveness of this modeling will be confirmed or not, by confrontation with the data collected by health authorities, knowing that the higher the number of data, the more accurate the statistical forecast.
The spread of Covid-19 is both exponential and erratic. In addition, the number of patients must be consolidated, because to contaminate does not cure the one who contaminates.
The exponential spread
The word exponential means that the variation factor appears as an exponant ; example : Sx means « S » to the power of « x » ; « S » multiplied by « S », « x » times : S x S x S . . .
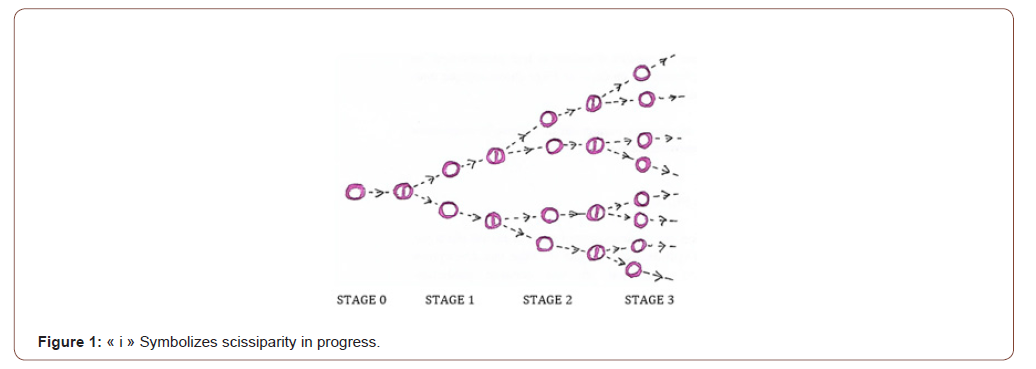
For example, bacteria double their number at each stage of their reproduction by scissiparity (Figure 1) (S = 2).
At stage number « 4 » we have 16 bacteria: 2 x 2 x 2 x 2 = 16, which can be written 24
. Stage number: 0 1 2 3 4 - - n
. Number of bacteria: 1 2 4 8 16 - - N
. Number written in power of two: 20 21 22 23 24 - - 2n
The number « N » of bacteria after « n » duplication is: N = 2n. inside an homogeneous environment, the passage from one stage to another occurs approximately at the same speed « v »; therefore n = v.t, then N = 2 v.t in which « v » is the only active factor. Indeed, « t » is what the clock of the laboratory indicates [5] (Figure 1).
If it were to triple at each stage, the numbers would be written in power of three. This is what is happening with the Covid-19 spread, according to the statistical average data, when no specific precautions are taken : one sick person contaminates three persons, each of them contaminates three persons, etc.
At each stage, the number of people infected triple on average (Figure 2). « 3 » is the average spread index « S ».
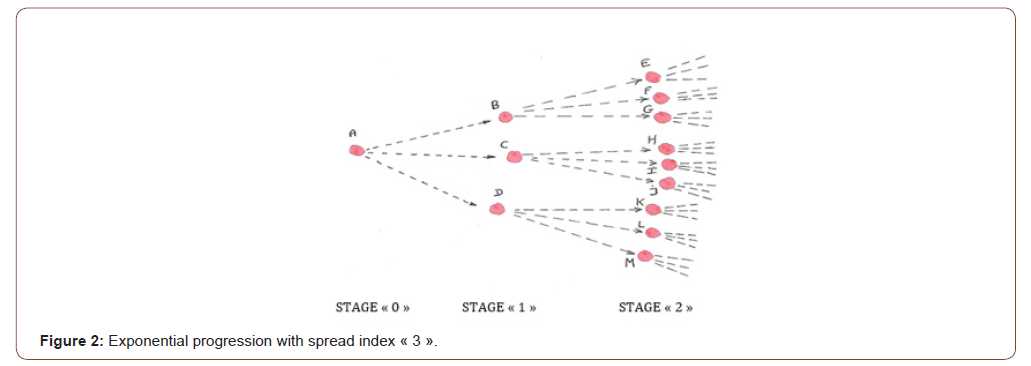
For example, 81 = 3 x 3 x 3 x 3 = 34; (« 3 » for « triple » and « 4 » for « stage number »).
. Stage number: 0 1 2 3 4 - - - n
. Number of people infected: 1 3 9 27 81 - - - N
. Number written in power of three: 30 31 32 33 34 - - -3n
The number « N » of people infected at the stage number « n » is: N = 3n.
This way of mathematical writing has the advantage of indicating both spread index and stage number (Figure 2).
The erratic spread
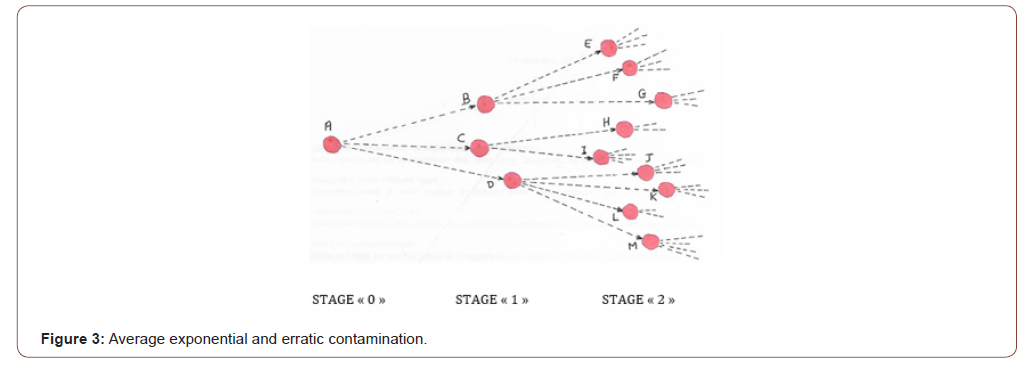
Figure 2 is a simplified representation of the phenomenon, because in fact, the transmission of the virus is erratic. One patient is able to infect more or less 3 persons.
The contamination time from a sick person to a healthy person is variable, a few days, a couple of weeks, or not at all; it is stochastic. « n » is no more proportional to time.
The times variability is represented by doted arrows whose length is proportional to time.
Figure 3 is an example in which « C » is infected before « B ». « D » is infected later. and it is infecting four people « J », « K », « L », « M », while « C » has infected only « H » and « I ».
The contamination times are unpredictable, as well as who is going to be infected or not.
N = Sf(t), in which f(t) is related to time according to a statistical feedback to be developed (Figure 3).
Data consolidation
Unlike the scissiparity of bacteria, the patient who infects someone remains sick: there is a cumulative effect.
Some patient are positive but not sick, some are sick and for a long time; accordingly, the statistical approach is based on average data, however it leads to a useful appraisal.
The cumulative number of patients at the second stage is: 9 + 3 + 1 = 13.
At the third stage: 13 + 27 = 40.
At the fourth stage: 40 + 71 = 121.
It explains why hospitals were so quickly crowded.
Control of the Spread
As long as no protective measures were taken, the average spread rate was about « 3 »: S#3.
Elevators are among numerous examples of high risk areas where « S » is much higher than « 3 », because they are often crowded, they carry a continuous flow of diverse users, and they are poorly ventilated in regard to high density of infected misty air of aerosol type. A carrier of the virus can infect several dozens healthy people. It’s better for your health to take the stairs!
The following statistical simulations prove how prominent is the spread index. Here is an estimate of the number « N » of patients infected at the fourth stage, with three different values of « S »:
First example when S # 1.2, then N = 1.2 x 1.2 x 1.2 x 1.2 = 2.07
The average number of new patients infected almost doubles from stage « 0 » to Stage « 4 ».
Second example when S # 0.8, then N = 0.8 x 0.8 x 0.8 x 0.8 = 0.4
The average number of new patients infected is divided by two from stage « 0 » to stage « 4 ».
Third example when S # 0.2, then N = 0.2 x 0.2 x 0.2 x 0.2 = 0.0016
Although the spread index is lowered, the number of patients infected is decreasing, but asymptotically : it won’t never reach zero. It means that the virus is still around ; hence the urgent need for drugs and vaccine.
Conclusion
The statistical modeling allows one to have an appraisal of the viral threat. So far, we don’t know how long the pandemic will last. In the meantime, health authorities of all countries will have to collect a bunch of accurate data, in order to feed statistical modelings, improve laws in force and work out new laws for neutralizing the impressive spread of Covid-19. We now know that a premature relaxation of behaviors would lead to a major blowback.
Acknowledgement
None.
Conflicts of Interest
No conflicts of interest.
References
- Dassonville P (2017) The Invention of Time & Space.
- Andre Leicknam B, Ziegler Ch Birth of writing; cuneiforms and hieroglyphs (National Museums - Paris 1982).
- Strabo (c.64 BC-c.22 AD): Geography (Remacle.org).
- Carpiceci (AC) Wonderful Egypt of the Pharaohs (JM Collet - Brussels 1980).
- Dassonville P (2018) The Aging Process and Time, in Peer Reviewed Journal of Forensic & Genetic Sciences. Lupine Publishers, New York.
-
Patrice F Dassonville. Mathematical Modeling of Covid-19 Spread. 4(5): 2020. ABEB.MS.ID.000599.
-
Erratic, Exponential, Multidisciplinary, Spread Index, Three-Dimentional, Physical phenomena, Architectural projects, Financial policy, Demographic statistics
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






