Chemical Reactors Catalyst bed and Analytical Solution of Complicated Partial Nonlinear Differential Equations by new Approach AKLM

In the study, our aims introduce of accuracy, capabilities and power for solving complex non-linear partial differential in the reaction chemical on the reactor’s catalyst bed. AKLM method can be successfully applied in various engineering fields such as mechanics (solid and fluid), electronics, petroleum industry, designing chemical reactors [1,2], and also in applied sciences (physics), economics and so on. It is worth noting that these two methods are convergent at any form of differential equations, including any number of initial and boundary conditions. During the solution procedure, it is not required to convert or simplify the exponential, trigonometric and logarithmic terms, which enables the user to obtain a highly precise solution. Besides, the methodology behind these techniques are completely understandable, easy to use, and users with common knowledge of mathematics will be capable of solving the most complicated equations at low calculation cost. As all experts know most of engineering actual systems behavior in practical are nonlinear process and analytical scrutiny these nonlinear problems are difficult or sometimes impossible. Our purpose is to enhance the ability of solving the mentioned nonlinear differential equations at chemical engineering and similar issues with a simple and innovative approach which entitled “Akbari- Kalantari-Leila Method” or “AKLM”. He’s Amplitude Frequency Formulation method [3-5] which was first presented by Ji-Huan He gives convergent successive approximations of the exact solution and Homotopy perturbation technique HPM [6]. It is necessary to mention that the above methods do not have this ability to gain the In the study, our aims introduce of accuracy, capabilities and power for solving complex non-linear partial differential in the reaction chemical on the reactor’s catalyst bed. AKLM method can be successfully applied in various engineering fields such as mechanics (solid and fluid), electronics, petroleum industry, designing chemical reactors [1,2], and also in applied sciences (physics), economics and so on. It is worth noting that these two methods are convergent at any form of differential equations, including any number of initial and boundary conditions. During the solution procedure, it is not required to convert or simplify the exponential, trigonometric and logarithmic terms, which enables the user to obtain a highly precise solution. Besides, the methodology behind these techniques are completely understandable, easy to use, and users with common knowledge of mathematics will be capable of solving the most complicated equations at low calculation cost. As all experts know most of engineering actual systems behavior in practical are nonlinear process and analytical scrutiny these nonlinear problems are difficult or sometimes impossible. Our purpose is to enhance the ability of solving the mentioned nonlinear differential equations at chemical engineering and similar issues with a simple and innovative approach which entitled “Akbari- Kalantari-Leila Method” or “AKLM”. He’s Amplitude Frequency Formulation method [3-5] which was first presented by Ji-Huan He gives convergent successive approximations of the exact solution and Homotopy perturbation technique HPM [6]. It is necessary to mention that the above methods do not have this ability to gain the

We consider an isothermal reaction and also, we assume governing chemical reaction equation on the solid catalyst bed in the chemical reaction are complicated and according of mathematical equations as follows:

1. By assuming that on the catalyst bed the reaction chemical for component A is as follows:

For cylindrical coordinate with radii R (n=1)

(Figure 1) By substituting the chemical reaction Equation (2) into the partial differential equation Equation (3), the result the following a complicated nonlinear partial differential equation in the cylindrical coordinate for reactants in catalytic chemical reactions as follows:

Output of the solution process by new approach AKLM (Akbari- Kalantari-Leila Method) for partial nonlinear differential equation Equation (5), according to the boundary and initial Equation (6) and the physical values Equation (7) at the cylindrical coordinate system figure (1), the solution of the differential equation is obtained as follows:

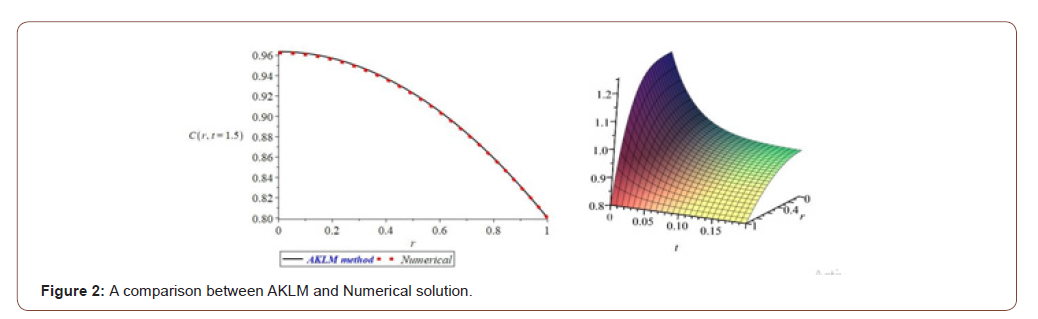
Comparing the achieved solutions by Numerical Method and AKLM

Due to the obtained solution from Equation (8) by AKLM, and Numerical method (Runge-Kutte 4th), we have the following comparisons:

(Figure 2) Concentration-time and reaction rate graphs as follows:

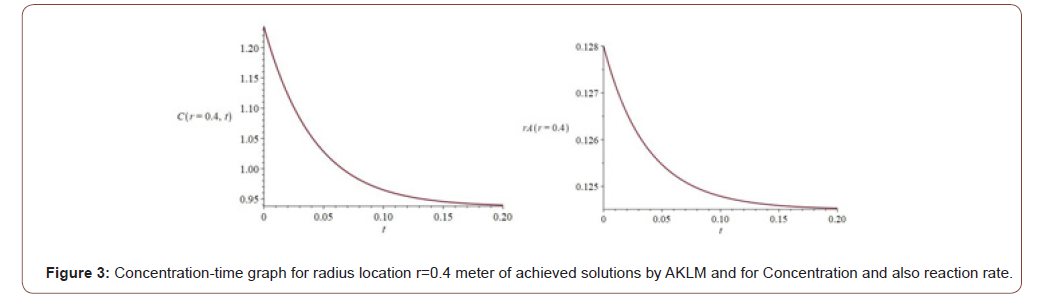
(Figure 3) In the concentration-time diagram for contour plot as follows:

(Figure 3) Charts of contour of AKLM solution for C(r,t).

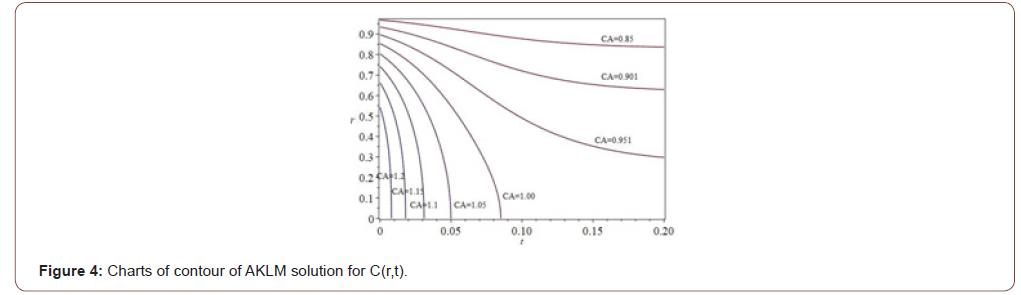
In the concentration-time diagram for contour plot as follows (Figure 4)

For cylindrical coordinate (n=2)

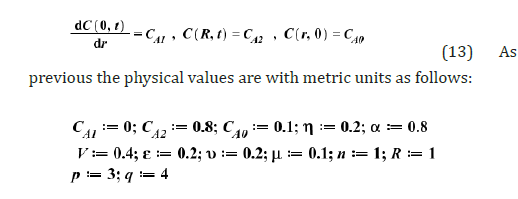
(14) Output of the solution process by new approach AKLM (Akbari-Kalantari-Leila Method) for partial nonlinear differential equation Eq.(12), according to the boundary and initial conditions Eq.(13) and the physical values Eq.(14) at the spherical coordinate system fig.(5), the solution of the differential equation is obtained as follows:

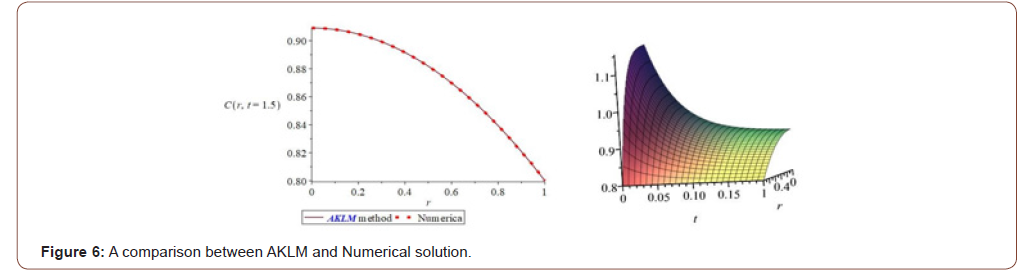
Comparing the achieved solutions by Numerical Method and AKLM

Due to the obtained solution from Equation (15) by AKLM, and Numerical method (Runge-Kutte 4th), we have the following comparisons:

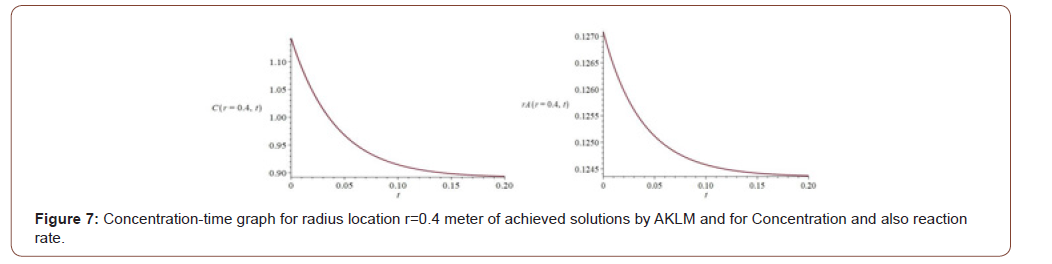
(Figure 6) Concentration-time and reaction rate graphs as follows (Figure 7)

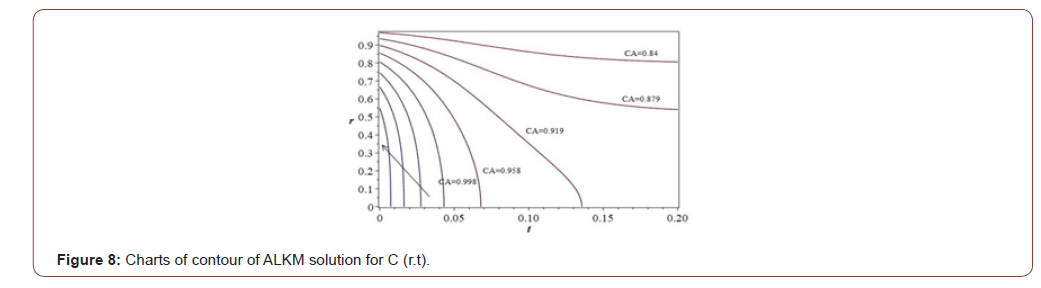
In the concentration-time diagram for contour plot as follows (Figure 8)

For cartesian coordinate (j=0)

(Figure 9) As previous we assume that on the catalyst bed the reaction chemical for component A is as follows:

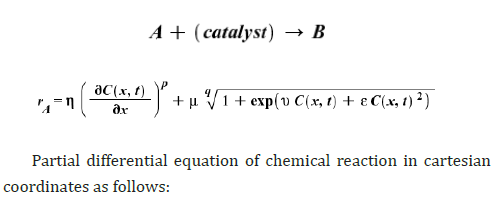
Output of the solution process by new approach AKLM (Akbari- Kalantari-Leila Method) for partial nonlinear differential equation Eq.(19), according to the boundary and initial conditions Equation (20) and the physical values Equation (21) at the slab coordinate system figure (9), the solution of the differential equation is obtained as follows:

Comparing the achieved solutions by Numerical Method and AKLM

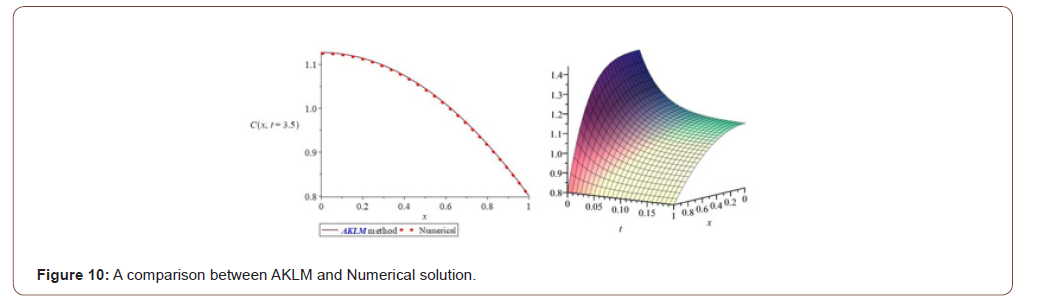
Due to the obtained solution from Equation (22) by AKLM, and Numerical method (Runge-Kutte 4th), we have the following comparisons:

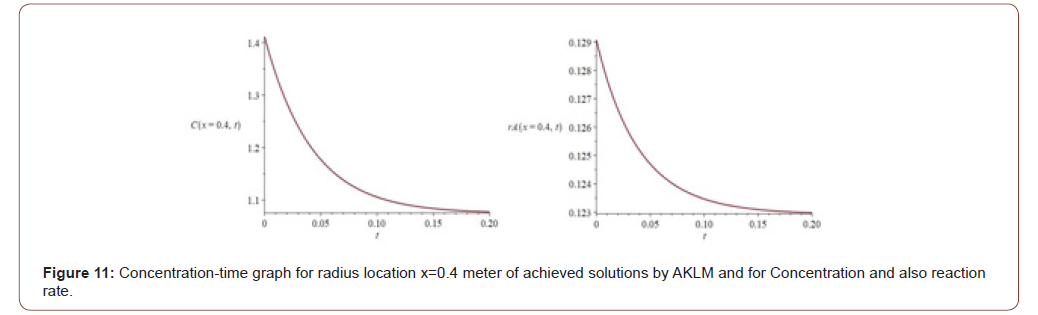
(Figure 10) Concentration-time and reaction rate graphs as follows:

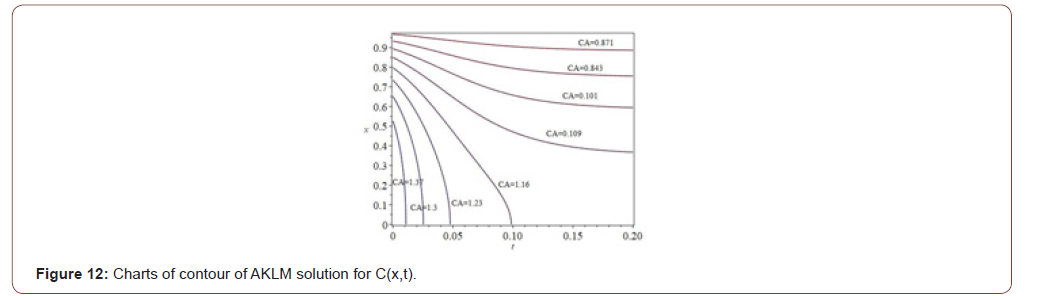
(Figure 11) In the concentration-time diagram for contour plot as follows:

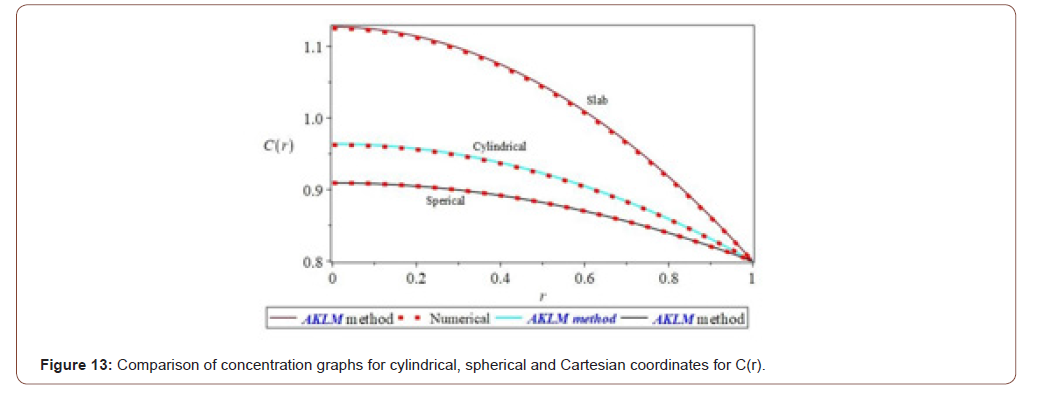
(Figure 12) Comparison of concentration graphs for cylindrical, spherical and Cartesian coordinates (Figure 13, 14)

In this article, we proved that we can with new method (AKLM) all kinds of complicated practical problems related to nonlinear partial differential equations in the design of chemical reactors can be easily solved analytically. Obviously, most of the phenomena of chemical reactions in chemical reactors are nonlinear, so it is quite difficult to study and analyze nonlinear mathematical equations in this area, also we wanted to demonstrate the strength, capability and flexibility of the new AKLM method(Akbari-Kalantari-Leila Method). This method is newly created, and it can have high power in analytical solution of all kinds of industrial and practical problems in engineering fields and basic sciences for complex partial nonlinear differential equations.

None.

No Conflicts of Interest.

1. Bruce A Finlayson, Brigette M, Rosendall, University of Washington Seattle, WA 981951750, Bechtel Technology and Consulting San Francisco, CA 94119-3965.
2. D Zwillinger, Handbook of Differential Equations (New York: Academic Press, 1992).
3. JH He (2008) An improved amplitude-frequency formulation for nonlinear oscillators. International Journal of Nonlinear Sciences and Numerical Simulation 9 (2): 211.
4. ZF Ren, GQ Liu, YX Kang, HY Fan, HM Li, et al. (2009) Application of he’s amplitude frequency formulation to nonlinear oscillators with discontinuities. Physica Scripta 80(4): 45003,
5. JH He (1998) Approximate analytical solution of Blasiu’s equation. Commun Nonlin Sci Numer Simul 3(4): 260-263.
6. JH He (1999) Homotopy perturbation technique. J Comput. Methods Appl Mech Engrg. 178(3-4): 257-262.
7. Book Nonlinear Dynamic in Engineering by Akbari-Ganji's Method
8. MR Akbari, Sara Akbari, Esmaeil Kalantari (2020) Akbari-Ganji‟s method “AGM” to chemical reactor design for non-isothermal and non-adiabatic of mixed flow reactors. Journal of Chemical Engineering and Materials Science 11(1): 1-9.
9. MR Akbari, DD Ganji, M Nimafar (2014) Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach. Frontiers of Mechanical Engineering Journal 9: 390-401
10. AK Rostami, MR Akbari, DD Ganji, S Heydari (2014) Investigating Jeffery-Hamel flow with high magnetic field and nanoparticle by HPM and AGM. Cent Eur J Eng 4(4): 357-370.
11. MR Akbari, DD Ganji, A Majidian, AR (2014) Ahmadi Solving nonlinear differential equations of Vanderpol, Rayleigh and Duffing by AGM. Frontiers of Mechanical Engineering 9: 177-190.
12. DD Ganji, MR Akbari, AR Goltabar (2014) Dynamic Vibration Analysis for Non-linear Partial Differential Equation of the Beam - columns with Shear Deformation and Rotary Inertia by AGM. Development and Applications of Oceanic Engineering (DAOE) 2325-3762.
13. MR Akbari, DD Ganji, AR Ahmadi, Sayyid H, Hashemi kachapi (2014) Analyzing the Nonlinear Vibrational wave differential equation for the simplified model of Tower Cranes by (AGM). Frontiers of Mechanical Engineering 9(1): 58-70.
14. MR Akbari, M Nimafar, DD Ganji, MM Akbarzade (2014) Scrutiny of non-linear differential equations Euler Bernoulli beam with large rotational deviation by AGM. Springer 9:402-408.
15. MR Akbari, Sara Akbari, Esmaeil Kalantari (2020) A Study about Exothermic Chemical Reactor by ASM Approach Strategy. Crimson Publishers Wings to the Research.