 Research Article
Research Article
Utility-Based Dose-Finding in Practice: Some Empirical Contributions and Recommendations
Jihane Aouni1,2, Jean Noel Bacro2, Gwladys Toulemonde2,3 and Bernard Sebastien1
1Sanofi, Research and Development, 91385 Chilly-Mazarin, France
2IMAG, Univ Montpellier, CNRS, Montpellier, France
3Lemon, Inria
Jihane Aouni, Sanofi, Research and Development, 91385 Chilly-Mazarin, France.
Received Date: July 24, 2019; Published Date: August 22, 2019
Abstract
Aspects related to dose-finding trials are of major importance in clinical development. Poor dose selection has been recognized as a key driver of failures in late phase development programs and postponements in drug approvals. The aim of this paper is to develop a flexible utility-based dose selection framework for phase II dose-finding studies that has satisfactory operating characteristics. This framework also allows to plan interim analyses with stopping rules that can be easily defined and interpreted by the clinical team within this same framework.
Keywords: Adaptive trials; Decision rules; Dose selection; Interim analysis; Utility function
Introduction
Because of the growing importance of dose-finding trials, we aim to address the problem of dose selection in clinical development with the point of view of utility functions [1-8] and utility maximization. The topics of dose selection and also of dosefinding studies are studied in their various aspects: decision rules, study designs (fixed versus adaptive designs) and statistical analysis methodology. The objective of this paper is to propose and study a Bayesian decision-making framework based on a utility function explicitly accounting for efficacy and safety modelling, where safety could be characterized by the absence of Adverse Events (AEs) for instance, and to assess related decision rules. This utility function is suitable and relevant with respect to the decisions the sponsor has to make: design the phase II trial, define the timing of the interim analysis, decide to continue in phase III or not and choose the dose for phase III when relevant.
For conducting the analysis and identifying the optimal dose, we advocate for the use of a Bayesian method, instead of a frequentist maximum likelihood approach, because it has the advantage of providing a richer set of dose selection rules aiming at choosing the best dose among the tested ones in phase II. Moreover, by definition of the Bayesian approach, it allows the sponsor to use external information already available.
Material and methods section is devoted to the mathematical formalization of the dose-response modelling approach, the definition of our proposed utility function and each of its components, the decision-making framework including the sponsor’s strategies to choose the optimal dose, the Go/NoGo decision rules, the relative utility loss criterion to make recommendations on phase II sample size, and the decision criteria/rules to stop at the interim analysis. At the end of this section, we describe our simulation protocol and our chosen simulation scenarios. In the Results section, we perform simulation analyses, comparing the proposed decision rules for dose selection. The selection of doses (number and spacing) is also discussed in terms of sensitivity of the framework to such aspects; the properties of the operating characteristics in this respect are explored. On the other hand, we assess, through simulations, the influence of phase II sample size, based on the relative utility loss criterion, and we compare different (fixed, adaptive) designs based on the suggested stopping criteria for interim analysis. This section is complemented by an analysis example based on a real dose-finding study. Finally, the Discussion and Conclusions section consists in summarizing our decision-making framework (decision rules for dose selection, and decision criteria for phase II recommendations and interim analysis).
Material and Methods
In this section, we delineate the common materials and methods applied to the work contained within this paper. We specifically describe the mathematical formalization of a phase II/phase III development program, aiming to define all necessary notations and calculations related to the dose-response modelling of efficacy and safety, to the Probability of Success (PoS), to the decision rules regarding the choice of the optimal dose, Go/No decisions, phase II sample size recommendations and interim analysis, and to the simulation protocol/scenarios. Note that ’Success’ is defined as significant comparison of the selected dose versus placebo in the phase III trial. Therefore, the PoS is, in our setting, the power of the phase III trial.
Dose-response modelling
In this paper, we model efficacy through a three-parameter Emax model [9-11], and safety through a Probit model, both described thereafter. A placebo and K active doses are considered, where a dose is denoted by d. The random efficacy response of patient i is represented by Yd,i, with i = 1, ..., nd, where nd is the number of patients for the dose d in phase II study; this random response is assumed to follow a Normal distribution N (m(d;θ ),σ 2 )where m(d;θ ) is the expected mean effect of dose d, and σ is the residual variability (standard deviation of residual error) assumed to be known. The empirical mean responses in dose d and placebo are denoted by ϒd and ϒ0 respectively, and we note Δ(d ) the difference of the two. Phase II and phase III sample size are respectively denoted by N2 and N3, where N3 is fixed and equal to 1000.
Regarding the modelling of efficacy, we used the following
three-parameter Emax model: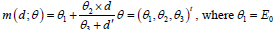 is the placebo effect,
is the placebo effect,
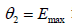 is the maximum effect compared with placebo and
is the maximum effect compared with placebo and
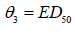 is the dose with half of the maximum effect.
is the dose with half of the maximum effect.
Regarding the modelling of safety, we used the
following Probit model: 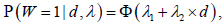
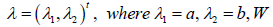 is the binary toxicity outcome
for one patient, 1 for occurrence of at least one Adverse Event (AE)
and 0 for absence of AE, and Φ is the Cumulative Distribution
Function (CDF) of the standard normal distribution.
is the binary toxicity outcome
for one patient, 1 for occurrence of at least one Adverse Event (AE)
and 0 for absence of AE, and Φ is the Cumulative Distribution
Function (CDF) of the standard normal distribution.
Utility function
Utility functions, defined as the opposite of loss functions [12], are generally introduced within the decision theory framework [13]. Utility describes the preferences of the “decision maker” and classifies/orders decisions. A decision theory result suggests that, in a risky environment, all decision rules can be compared and classified using the expectation of a given utility function. When conducting a clinical trial, there is an alternation of decisions (choice of doses, sample size, etc.) and observation of random data (as in patients responses). The multitude of these possible cases can be translated into utility functions to be defined according to expectations and goals. Dose optimality can be formalized thanks to such functions, representing the benefits of the stage 2 and the final dose recommendation.
In this paper, we preferred to focus on utility functions only defined by medical/clinical properties of the compound as we believe that costs, and more importantly, financial reward (in case of successful development) are difficult to precisely quantify in phase II. Therefore, we propose a straightforward and workable definition of the utility function, with two components, one related to efficacy and the other related to safety. The PoS (which is the power of a phase III trial with a fixed sample size) represents the dose efficacy and can be computed using standard calculations. For the case of a balanced phase II trial:
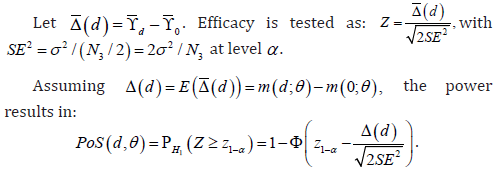
On the other hand, we chose to express safety according to the
probability of observing a toxicity rate lower than or equal to a
thresholds in the dose arm, during a phase III trial of N3 patients
in total: the number of patients having an AE in the phase III trial is
a binomial distribution of parameters N3/2 and Ρ(W =1| d,λ ); the
quantity toxobs is the observed proportion of patients having AEs in
phase III, 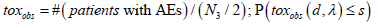
is then the predictive probability of controlling over-toxicity (due to AEs), i.e. the predictive probability of observing a toxicity rate ≤ s in phase III. Note that in practice, the choice of the s value should depend on the clinical team project and the related therapeutic area.
We considered then utility functions of the following form:
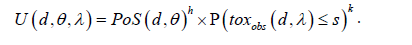
Parameters h and k reflect the respective contributions of efficacy and safety to the utility function. They are project dependent and must be chosen according to the context. For instance, for a rare disease indication for which there is a clear unmet medical need, there should be less constraint on safety: therefore low values of k should be chosen. On the contrary, for a very competitive therapeutic area, more constraint should be put on the safety side, therefore large values of k should be chosen. There are several ways to combine the efficacy and safety components: an additive approach, of the form U=Efficacy component + Safety component, could be used as well. We have chosen a multiplicative form because, according to us, it leaves less room for compensation of the weakness in one of the two components by the other one.
For the sake of simplicity, and in order to facilitate the reading, in the following of the paper, we will drop the parameters in the notations of the quantities of interest when there is no ambiguity. For instance, we will note PoS(d) instead of PoS (d,θ ), Ρ(toxobs(d)) instead of Ρ(toxobs(d,λ)) U(d) instead of U(d,θ,λ), etc.
We use a MCMC approach [14,15], particularly a Metropolis Hastings algorithm to capture the posterior of the PoS for the purpose of dose selection. Samples from the posterior of the PoS can be obtained from MCMC iterations:
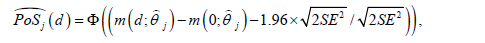
where 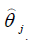 is the point estimate of the vector of efficacy
model parameters θ obtained at iteration j. The same procedure
is implemented to estimate the safety model parameters. The
advantage of Bayesian framework over a purely frequentist
approach lies in its ability to account for the uncertainty in
parameter values in the decisional process and also, in allowing
greater flexibility in the definition of the decision rules.
is the point estimate of the vector of efficacy
model parameters θ obtained at iteration j. The same procedure
is implemented to estimate the safety model parameters. The
advantage of Bayesian framework over a purely frequentist
approach lies in its ability to account for the uncertainty in
parameter values in the decisional process and also, in allowing
greater flexibility in the definition of the decision rules.
Decision-Making Framework
Sponsor’s strategy: Optimal dose and decision rules
In the following, we compare various decision rules related to the choice of dose by the sponsor. We consider five decision rules that are described thereafter. Note that 1000 phase II studies are simulated, each study contains 1000 MCMC iterations.
For each study, the sponsor makes two decisions regarding the fixed design:
Dose selection: the sponsor chooses the optimal dose d* according to one of the decision rules discussed in the following: Decision rule 1, Decision rule 1*, Decision rule 2, Decision rule 3 and Decision rule 4.
Go/ NoGo decision: the sponsor computes the average of PoSs and the average of the toxicity probabilities for the recommended dose d* among all MCMC iterations denoted by:
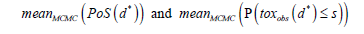
respectively.
The ’Go’ for phase III is then decided if these averages pass prefixed efficacy and toxicity thresholds denoted by threshold. eff2 and threshold.safe2, respectively. In other words, the sponsor chooses ’Go’ if:
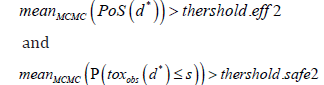
This decision-making described above is applied at the study level (efficacy and safety constraints are applied for each simulated phase II study). A more restrictive approach would be to apply constraints at the MCMC level, in addition to the ones applied at the study level (for each MCMC iteration, efficacy and safety constraints are applied, in a similar way to those applied for each study). This alternative strategy (referred to as “Decision rule 1*” in the following) is described thereafter.
Comparisons of several decision rules
The aim is to compare various decision rules, through simulations, and visualize their performances through the relative utility loss (defined below) graph (see Figure 2 and Table 1). To do so, we will work on the decision rule of the sponsor (choice of dose), by comparing simulation results with different possible alternatives:
• Decision rule 1: dose that has the greatest probability of being the best is selected
• Decision rule 1*: dose that has the greatest probability of being the best, with additional constraints at the MCMC level (modified version of Decision rule 1, see discussion below), is selected
• Decision rule 2: dose that maximizes ( ) E MCMC U is selected
• Decision rule 3: dose that maximizes 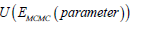 is selected
is selected
Decision rule 4: dose that maximizes 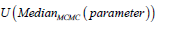 is selected
is selected
Decision rule 1* is a slightly different version of Decision rule 1; it is defined as follows: the main idea is the same, selecting the dose that is the most likely (according to posterior distribution) to be the optimal dose, but the implementation is slightly different. In order to avoid that the selected dose although having likely the highest utility has at the same time either a too low PoS or a too high probability to have an observed toxicity rate > s, we modified the dose selection algorithm. We selected the dose with highest probability to be the optimal one with respect to a modified utility denoted by U′ . This latter utility U′ has the same values than U, but is set to 0 when the PoS is either lower to a given threshold (threshold.eff1) or when the probability of having an observed toxicity ≤ s is lower than another threshold (threshold.safe1). These thresholds are applied at the MCMC level. In other words, this modified utility function can be defined, at each MCMC iteration, as follows:
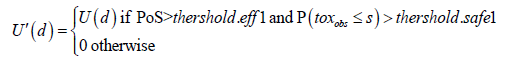
By applying efficacy and safety rules (at both MCMC and study levels), the sponsor is more restrictive regarding the dose choices.
We have chosen the relative utility loss as a metric to rank
these five decision rules proposed above; it is defined as the
difference between the expectation of the utility induced by
the considered decision rule and the maximum true utility
value within the K doses, named Umax, divided by this same
maximal value UmaxIt enables to characterize the quality of the
decision rule, through its relative proximity to the ideal best
decision rule (always select the optimal dose). It can be defined as follows:
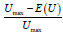 where E (U ) is the Umax empirical utility expectation of the chosen dose d* for the 1000 simulated phase II
trials.
where E (U ) is the Umax empirical utility expectation of the chosen dose d* for the 1000 simulated phase II
trials.
Influence of phase II sample size - sample size recommendations
In the following, we propose a criterion allowing to choose the sample size of phase II: we will discuss the necessary sample size according to a utility criteria (and not according to power criteria as usually done). For instance, the sample size would be defined as follows: “if the profiles of efficacy and safety are of such type then X patients are required in phase II to have 90% of the maximal utility. If the efficacy and safety profiles are of another type then it takes Y patients in phase II to have 90% of the maximal utility”.
This necessary sample size obviously depends on the profile that is unknown, but this is common practice; in order to have more robustness for the power calculations, several alternative scenarios are assessed or, more recently (see [16]), prior distribution are considered for Δ and σ in order to have some Bayesian-averaged sample size calculation. A very similar approach can be used with the new methodology we propose: in the simulation-based sample size calculation, instead of simulating studies with the same hypothesized fixed value of the efficacy and safety parameters, those structural parameters could be sampled from prior distribution representative of the sponsor’s expectation related to the new drug.
Our recommendations will be of the same type, even richer (assumptions on both efficacy and safety) and the sample size will not guarantee a power of 90%, if the assumptions are true, but 90% of the maximum utility: this could be a new approach consistent with the true objective of the phase II study (recommending a safe and active dose for phase III study).
In the Results section, and with Decision rule 1, we apply the above criterion allowing to judge whether the phase II sample size is sufficient or not. This criterion is based on the importance of the relative loss of utility previously defined: one can say that the size N2 is sufficient if the global estimation of the utility expectation (over all simulated phase II studies) reaches 90% (or maybe less, 80% for example) of the maximum utility. This gives an idea of necessary sample size of phase II. Then we can vary the efficacy and safety scenarios and decide which is the necessary sample size of phase II according to the efficacy and safety profiles. For each profile, the determination of this sample size is based on the relative loss of utility graphs, which is plotted for each profile (see Figures 3-6).
We also compare the phase II recommendations based on this
relative utility loss criterion to their corresponding phase II powers,
denoted by 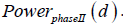 These powers can be considered
as reference values allowing to judge the interest of this new
approach, i.e. of choosing between 80% or 90% of the maximum
utility. The phase II power is calculated for each dose separately
versus placebo, for a unilateral test at 5% level. No adjustment for
multiplicity is performed.
These powers can be considered
as reference values allowing to judge the interest of this new
approach, i.e. of choosing between 80% or 90% of the maximum
utility. The phase II power is calculated for each dose separately
versus placebo, for a unilateral test at 5% level. No adjustment for
multiplicity is performed.
Criteria for interim analysis
A sub-issue of this paper is to perceive if an interim data inspection strategy for phase II, when N2′ < N2 patients are enrolled, can significantly reduce the mean sample size (consequently, budget and time as well) while maintaining the properties of the design (good decision quality of the dose for the phase III). To do so, an adaptive design (with futility and efficacy rules at the interim analysis) is compared to a fixed design in order to check the usefulness of interim analysis.
In the following, we consider several stopping rules criteria for the interim analysis, as well as several threshold values to stop at interim analysis.
For a given l value, 0 < l <1 the first stopping rule criterion for interim analysis is defined as follows:
stop at interim if
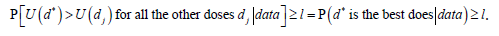
The choice of threshold l should be made prudently and should guarantee a fair compromise between accuracy of the dose choice, and the frequency of early termination at interim.
Another possible criterion for the interim analysis, inspired by [17], could be based on the difference of the means or medians of the utilities. The idea is to calculate the median or mean for each utility / iteration and calculate the median differences between each dose d1 and d2 and to check if these differences are at least equal to a given value, say X, in favour of a given dose. In other words, a dose d2 would dominate another dose d1 and could be preferred, if the difference between the two relative utility medians or means is at least X, in favour of d2. So we could define these criteria as follows:
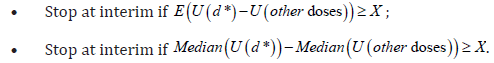
Strictly speaking, to justify a dose choice, one could imagine the following two domination criteria: a dose d2 would dominate another dose d1 and could therefore be preferred if the difference between the two means of the utility is at least X in favour of d2, or, a dose d2 would dominate another dose d1 and could therefore be preferred if the difference between the two medians of the utility is at least X in favour of d2. We call these criteria ’Domination criterion 1’ and ’Domination criterion 2’ respectively.
The decision for the interim analysis, based on the selected dose d* (with Decision rule 1 for instance) could then be defined as follows: if d dominates all other doses for one of the two domination criteria mentioned above, then stop and go to phase III with d*.
We will compare these three stopping rule criteria, via simulation, through the following four fixed/adaptives designs:
• Design 1: 100 patients in phase II.
• Design 2: 500 patients with interim analysis at 100 patients; at 100 patients, one determines the dose d*:
1. if one of the stopping rule criteria is met at interim 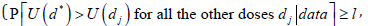 Domination
criterion 1, or Domination criterion 2), then stop
the study, and choose the optimal dose d*;
Domination
criterion 1, or Domination criterion 2), then stop
the study, and choose the optimal dose d*;
2. otherwise we continue to the final analysis with 500 patients.
• Design 3: 500 patients with interim analysis at 250 patients; at 250 patients, one determines the dose d*:
1. if one of the stopping rule criteria is met at interim 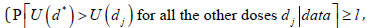 Domination
criterion 1, or Domination criterion 2), then stop
the study, and choose the optimal dose d*;
Domination
criterion 1, or Domination criterion 2), then stop
the study, and choose the optimal dose d*;
2. otherwise we continue to the final analysis with 500 patients. Design 4: 500 patients in phase II.
Our aim here is to obtain a simulation-based comparison between the following four utility expectations:
E(U(Design 1)), E(U(Design 2)), E(U(Design 3)) and E(U(Design 4)).
Since the utility increases with the sample size, we know that E(U(Design 1)) < E(U(Design 2)) < E(U(Design 3)) < E(U(Design 4)). But we hope to illustrate that Design 2 or Design 3 leads to quite similar expectation as Design 4, even if they are slightly less efficient (in terms of expected utility) than the latter one. Moreover, for situations where there is a dose that is clearly different/ distinguished from others, we hope to stop often at 100 patients or at 250 patients, and these designs will be more economical than Design 4.
Regarding futility rules at the interim analysis (i.e. stop at
interim and ’NoGo’), the same rules are applied as those for the
fixed design (i.e. ’NoGo’ at interim if 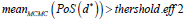 and
and 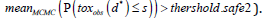
Simulation protocol and scenarios
A placebo denoted by d = 0 and four active doses denoted by d = 2, 4, 6, 8 are considered (to explore the impact of number of doses and dose spacing on the properties of the decision rules, we also add a new scenario with only 3 doses in addition to the placebo: d = 2, 4, 8). The residual variability σ is set to the value of 0.5 in the simulations. This value has been chosen in order to have, for one of our most important scenarios, named ”Sigmoid” (defined in the following), an effect size of 0.25 for the highest dose of our design.
We consider weakly informative priors for  and
non-informative prior for
and
non-informative prior for  follows a standardized Normal
distribution N(0, 1),
follows a standardized Normal
distribution N(0, 1), 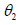 follows a Normal distribution N(0, 100), and
follows a Normal distribution N(0, 100), and
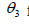 follows a Uniform distribution U[1,10].
follows a Uniform distribution U[1,10].
The following weakly informative prior distributions for the
parameters of the Probit model are considered: intercept 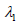 follows
a Normal distribution
follows
a Normal distribution 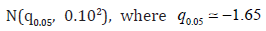 is the
normal distribution quantile which corresponds to 5% of toxicity
in placebo arm, and dose effect 2 λ
follows a Uniform distribution
U[0, 1].
is the
normal distribution quantile which corresponds to 5% of toxicity
in placebo arm, and dose effect 2 λ
follows a Uniform distribution
U[0, 1].
Concerning the choice of the threshold value related to the toxicity component of the utility function, we choose s = 0.15. We consider h = 1 and k = 2. Regarding efficacy and safety thresholds, we consider threshold.eff1=0.30, threshold.safe1=0.30, threshold. eff2=0.30 and threshold.safe2=0.50, for both fixed and adaptive designs. Regarding interim analysis, we compare simulation results for l = 0.80, l = 0.90, X = 0.10 and X = 0.20. All these values should be considered as examples rather than recommendations and the clinical team should wisely choose those values in practice, based on the project and indications.
We consider two main efficacy scenarios assumed to reflect the true efficacy dose-response:
• Sigmoid scenario: this scenario is monotonic, that is, the
mean response is strictly increasing as a function of the
dose; for this scenario, the true efficacy model parameters
values are: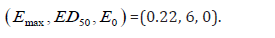
• Plateau scenario: this scenario begins with an almost
linear growth, followed by an inflection, and then
stabilizes at the end, which means that the last two doses
have the same efficacy; for this scenario, the true efficacy
model parameters values are:
We also consider two main toxicity scenarios assumed to reflect the true safety dose-response:
• Bad safety profile (scenario with a progressive toxicity); for this scenario, the true toxicity model parameters values are: (a,b)=(-1.645, 0.100), and the theoretical toxicities for doses d = 0, 2, 4, 6, 8 are: 0.05, 0.07, 0.11, 0.15, 0.20 respectively.
• Good safety profile (low toxicity scenario); for this scenario, the true toxicity model parameters values are: (a,b)=(-1.645, 0.045), and the theoretical toxicities for doses d = 0, 2, 4, 6, 8 are: 0.05, 0.06, 0.07, 0.08, 0.10 respectively.
Results
Comparison of decision rules
In the following, the relative utility loss graph and the simulation results are given for Sigmoid scenario with progressive toxicity scenario (and toxicity of highest dose = 0.20), for each of the decision rules defined in the previous section, see Figure 2 and Table 1. A graph displaying the corresponding theoretical curves is plotted (see Figure 1), where the black curve represents the PoS, the purple curve represents the toxicity probability, the ’Toxicity penalty’ red curve represents the probability of observing more than 15% of toxicity in phase III, and the green curve represents the utility.
Based on Figure 1, the optimal dose is the dose d = 4 and the true associated PoS and utility are both approximately equal to 0.8 (Figure 1).
The relative utility loss functions corresponding to the five decision rules we considered are presented in Figure 2.
In Figure 2, and its related table (Table 1), we can see that Decision rule 1, Decision rule 1* and Decision rule 2 are consistently better than Decision rule 3 and Decision rule 4 for all values of the sample size, but the difference between Decision rule 1, Decision rule 1* and Decision rule 2 versus Decision rule 3 and Decision rule 4 is particularly important for the sample size between 200 and 400 patients.
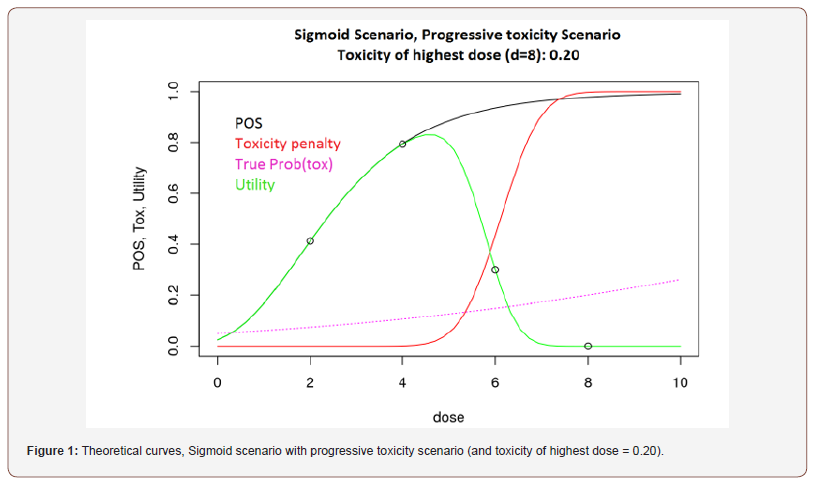
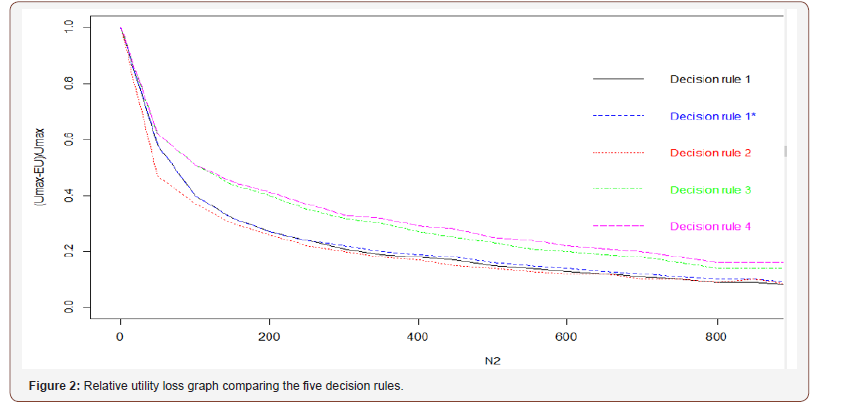
Table 1: Values of the relative utility loss depending on N2.
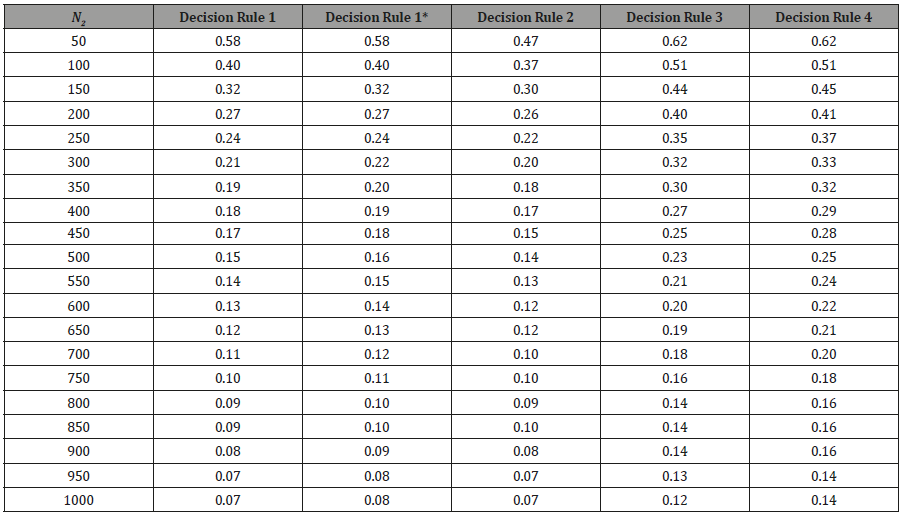
The Decision rule 2 is consistently better than Decision rule 1* and Decision rule 1, but the difference is small and almost negligible for the largest sample size (N2 > 700). However, Decision rule 2 (as well as Decision rule 3 and 4) does not take into account uncertainty. Here, the uncertainty is the same for all doses due to the balanced treatment groups, but in case of an unbalanced design or patients dropouts, this property will no longer be valid for Decision rule 2. Decision rule 1 or Decision rule 1* will then be more robust and more effective. Based on the graph and the table, Decision rule 1 is slightly better than Decision rule 1* (Table 1).
In order to confirm these results, we made, in the following, a more advanced comparison of these five decision rules, based on the 1000 simulated phase II studies. Tables summarizing the results over all simulated studies are given thereafter (see Tables 2-4). These tables contains the following: ’E(U)’ representing the empirical utility expectation of the chosen dose for the 1000 simulated phase II studies among ’Go’ and ’NoGo’ decisions (utility is set to 0 when it is a ’NoGo’ decision), ’Prob(choose(Go))’ representing the probability of going to phase III with the chosen dose, ’Distribution selected doses (Conditional to ’Go’)’ representing probabilities of choosing the d=2, 4, 6 and 8 dose respectively among the ’Go’, ’POS(conditional to ’Go’)’ representing the PoSs mean among the ’Go’ with the chosen dose, and ’Power’ representing the global power for the combined phase II / phase III program, defined as the product of ’Prob(choose(Go))’× ’POS(conditional to ’Go’)’. Moreover, to explore the impact of number of doses and dose spacing on the properties of the decision rules, we added a new scenario with only 3 doses in addition to the placebo: d = 2, 4 and 8. These results are given in blue in the following table columns, with Decision rule 1 as an example. The ’x’ symbol designates the missing dose d = 6 in the design considered for the exploratory analysis (Tables 2-4).
Based on Tables 2-4, we can see that with Decision rule 2, the dose choice is slightly better compared to Decision rule 1 and Decision rule 1*: one chooses d = 4 a bit more often (which is the true optimal dose according to theoretical curves), but the difference is small. However, results are quite similar in terms of expected utilities, probabilities of going to phase III, PoSs and global powers. Decision rule 1 is slightly better than Decision rule 1* in terms of expected utilities and dose choice. Decision rule 3 is clearly worse than Decision rule 1, Decision rule 1* and Decision rule 2. A possible explanation could be that the extreme values of the parameter estimates have an impact on the mean values used and accentuate an estimation bias. However, when considering the estimates median rather than estimates mean (Decision rule 4), we can see that results are very close to those obtained with the mean, even slightly worse.
Table 2: Simulation results, N2 = 250, comparison of five decision rules for dose selection.

Table 3: Simulation results, N2 = 500, comparison of five decision rules for dose selection.

Table 4: Simulation results, N2 = 1000, comparison of five decision rules for dose selection.

Regarding the exploratory analysis, results are quite similar when considering a smaller number of active doses and a different spacing: the loss of a non-optimal dose (we removed dose d = 6 which is not the optimal dose) did not decrease the decision and dose selection qualities. Globally, Decision rule 1, Decision rule 1* and Decision rule 2 lead to almost similar results and are consistently better than Decision rule 3 and Decision rule 4. Note that this result is also visually established by Figure 2.
We retained Decision rule 1 for the next subsections of this paper: the difference is small between Decision rule 1, Decision rule 1* and Decision rule 2, but, the Decision rule 1 (or Decision rule 1*) is easily understandable/interpretable by a clinical team, it better accounts for uncertainty in parameter values, and it fits well to a suitable rule for interim analysis. The reason why Decision rule 1 is retained, in the following subsections, in preference to Decision rule 1*, is discussed in more detail in the Discussion and Conclusions section.
Influence of phase II sample size
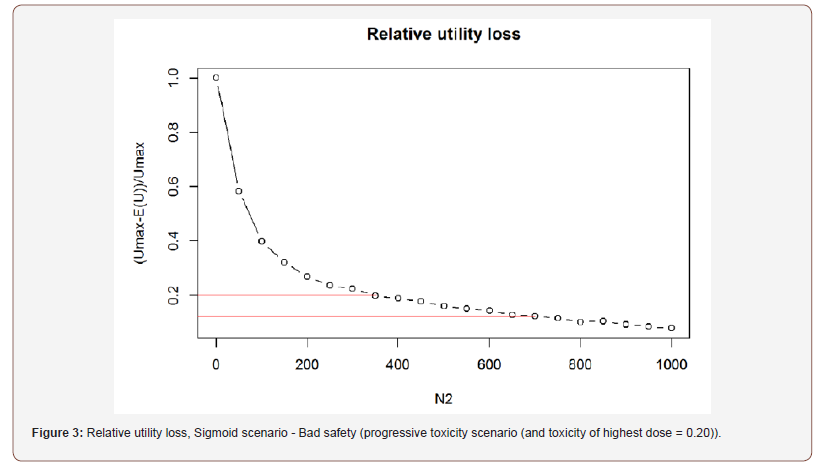
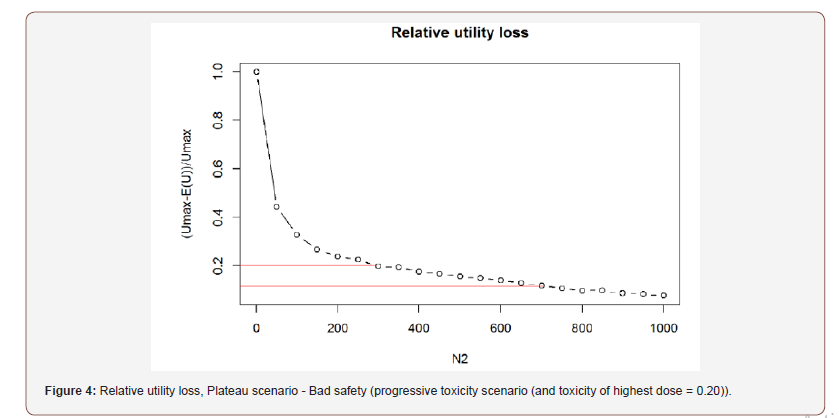
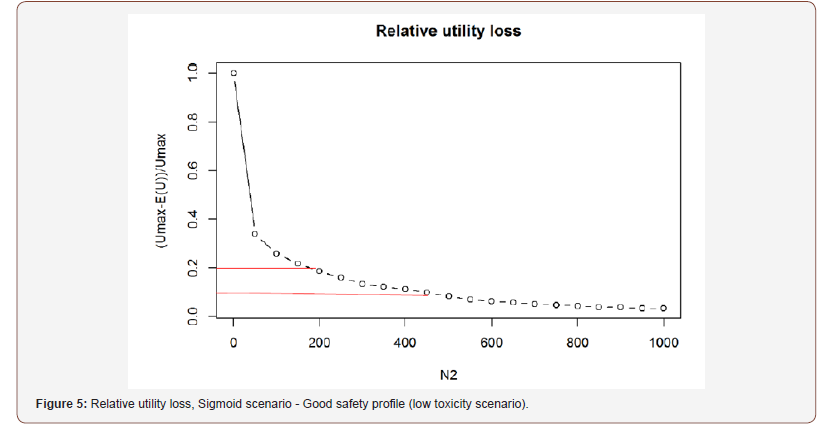
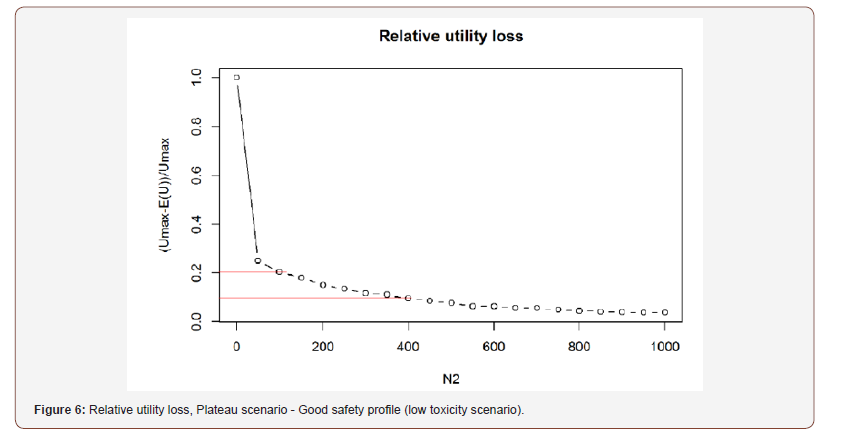
Below are the results of the sample size determination based on the utility criterion (relative utility loss) previously defined, with Decision rule 1. In Figures 3, 4, 5 and 6, the values of 0.2 and 0.1 (pointed out by red lines) correspond to a relative utility loss of 20% and 10%, respectively. So we will assess in the following, the number of patients required to reach 80% and 90% respectively of the maximal utility (Figures 3-6).
One could of course develop or imagine other combinations of efficacy/safety scenarios. Regarding the bad Safety profile (progressive toxicity scenario, and toxicity of highest dose =0.20), we have the following simulation results.
Sigmoid scenario (Figure 3):

Plateau scenario (Figure 4):

Sigmoid scenario (Figure 5):

Plateau scenario (Figure 6):

In those examples, the sample sizes proposed appear quite small, as compared to those necessary to reach the standard 80% or 90% of the classic phase II power. But one should keep in mind that selecting a dose for phase III (showing a favourable trade-off between efficacy and safety) is a totally different objective from that of searching for statistical significance. In fact reaching statistical significance is not the main objective of phase II (it is an objective for phase III), it is rather to propose the most appropriate dose for phase III.
Interim analysis
Regarding interim analysis, we consider the following combination of efficacy and safety scenarios: Sigmoid scenario with progressive toxicity scenario (and toxicity of highest dose = 0.20). Here also, the choice of the dose is governed by Decision rule 1. In the following tables (Tables 5-7), two additional columns are added as compared to the ones given previously:
(i) ’Prob(Stop at interim)’ representing the probability of stopping at the interim analysis
(ii) ’Mean(N2)’ representing the mean size for the adaptive plan (Table 5).
Based on Table 5, we can see that the utilities are well ordered (the larger the N2, the larger the empirical expectation E(U)). The interim analysis with l = 0.80 is effective, with a significant probability of stopping at interim (around 30% for both adaptive designs with 100 and 250 patients at interim analysis respectively). However, the interim analysis with l = 0.90 is not very useful: allowing ourselves to make a decision before the final analysis is a loss in the quality of the decision (compared to systematically wait for the final analysis) with such a restrictive threshold.
Table 4: Simulation results, stop at the interim analysis if Ρ(d* is the best dose|data) ≥ l, l = 0.80,0.90, interim at N′2 = 100 and N′N′2 = 250.
Table 5: Simulation results, stop at the interim analysis if Ρ(d* is the best dose|data) ≥ l, l = 0.80,0.90, interim at N′N′2 = 100 and N′2 = 250.
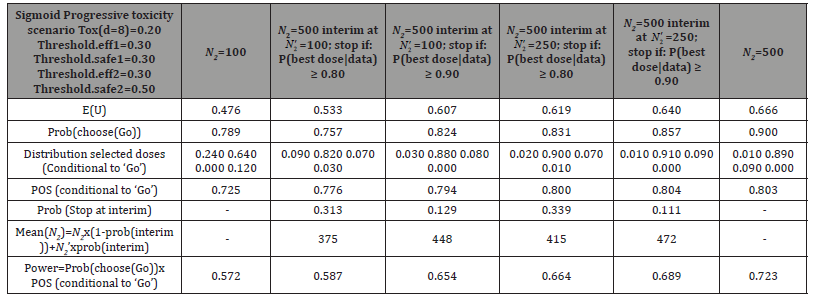
On the other hand, we can clearly see that E(U(Design 1)) < E(U(Design 2)) < E(U(Design 3)) < E(U(Design 4)), for both values of l. But E(U(Design 3)) is much closer to E(U(Design 4)) than E(U(Design 2)), and the best dose is clearly different/distinguished from others with this design (the probability of choosing d = 4 dose, which is the optimal dose according to theory, is higher with Design 3 compared to Design 2), which makes it more economical and more beneficial than Design 4.
So we have concluded that:
• l = 0.90 is too restrictive (not enough stops at interim analysis)
• l = 0.80 is economically more interesting: we stop more often at interim analysis, and consequently, we save patients (the average sample size of the phase II trial is reduced)
• In this example, Design 2 (design with N′2 = 100), underperforms Design 3 (design with 2 N′ = 250), for both values of l, 100 patients is not enough and yet we stop too often, which consequently leads to bad decisions
• Design 3 with l = 0.80 is beneficial because we stop quite often at interim (so we save patients) while maintaining the properties of Design 4 (fixed design with N2 = 500).
Table 6: Simulation results, utility mean differences criterion: Domination criterion 1 with X= 0.10, 0.20.
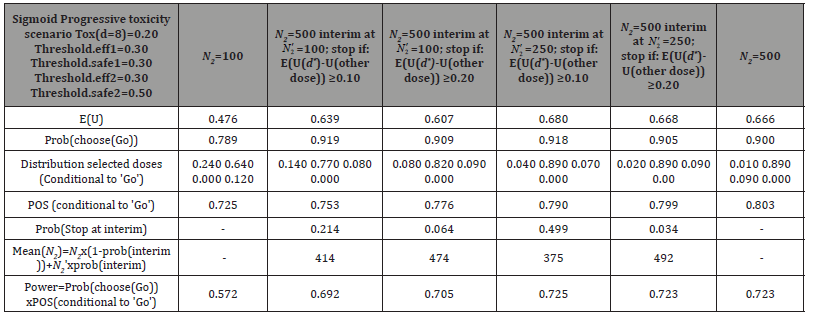
In Table 6, we used the utility mean differences criterion (Domination criterion 1), with X = 0.10, 0.20 (Table 6). Results with the utility median differences criterion (Domination criterion 2), with X = 0.10, 0.20, are given in Table 7.
Table 7: Simulation results, utility median differences criterion: Domination criterion 2 with X= 0.10, 0.20.
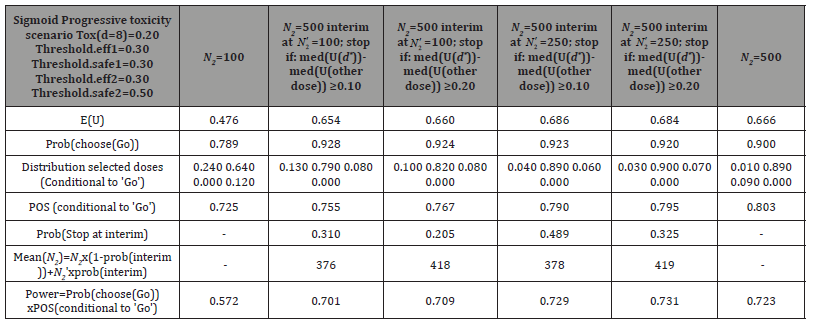
The "E (U (d* )−U (other doses)) ≥ 0.10" criterion is quite effective based on simulation results given in Table 6, but considering a higher threshold (0.20) becomes too restrictive, and consequently, not enough stops are recorded at the interim analysis. On the contrary, results with the utility median differences criterion, given in Table 7, are satisfactory when considering either the smaller threshold (0.10) or the higher one (0.20). The frequency of stopping at interim analysis decreased with the threshold of 0.20, but the difference is quite small as compared to the one with the first domination criterion (Table 6).
However, these domination criteria proposed above are complicated and not too intuitive: the “domination” definition is very arbitrary (difference of the medians of the utilities > 0.20 or 0.30 is very difficult to justify given the abstract nature of the utility). But such definition of domination criteria was motivated/ inspired by [17], where authors describe a phase II clinical trial for finding optimal dose levels, in a different context: patients allocation to doses. They use the following algorithm in order to design a sequential clinical trial: they propose a dynamic programming rule which consists in doing backward induction, and a well detailed algorithm is described in particular, alternating sequence of expectation and maximization. Utility-based decisions consist of dose selection, within a Bayesian framework, based on posterior probabilities: at every stage of the trial, the next patient is allocated to the selected dose, the trial may be stopped for futility, with no treatment recommendation, and doses may be dropped during the trial, if they are judged to be less effective than others. However, these doses are not totally excluded from the trial and may be reused in randomization, which consists in allocating patients to doses within the “non-dominated” set. Here, “non-dominated” set refers to the set of superior doses, dominating the others. Indeed, dropped doses may dominate other doses later on, when the posterior probabilities change: a dose may be inferior at a given time point, than superior at another time. Hence an adaptive randomization for dose allocation, carried out from sequential design, based on expected utility, to define the set of “non-dominated” doses.
The proposal based on stopping at the interim analysis if Ρ(d* is the best dose|data) ≥ l, is much more intuitive, it is simpler to explain to a clinician that phase II is stopped if the dose that we found has a probability > l of being the best, than to say that the dose ”dominates” the others on two different criteria that are rather arbitrary (based on the numerical value of utility, which is a very abstract quantity).
Example of Application in a type 2 Diabetes dose-finding study
As an illustration, we show thereafter how the method could be applied to a real dose-finding study. The results below are inspired from a phase II study in type 2 Diabetes. This study included 3 dose arms (doses=10 mg, 15 mg and 20 mg) plus a placebo arm as control. The design was a parallel group design with 60 patients per arm. The primary endpoint was the change from baseline in HbA1c (%) at week 26 (see Table 8). The safety criterion that was considered to compare the doses was the percentage of patients that discontinued treatment due to AE (see Tables 8 & 9).
Table 8: Efficacy results, mean (SD) change from baseline in HbA1c at Week 26.
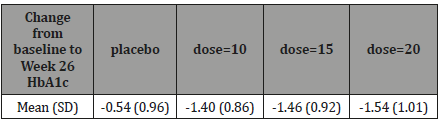
Table 9: Safety Results, % of premature discontinuation of patients due to AE.

Figures 7 and 8 show the observed and model predicted efficacy and safety profiles. We can notice a quite flat efficacy profile with little difference between doses (Figures 7 & 8).
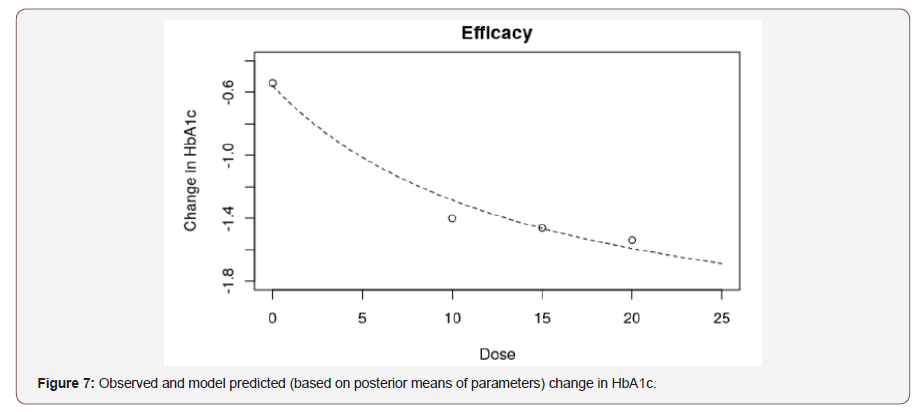
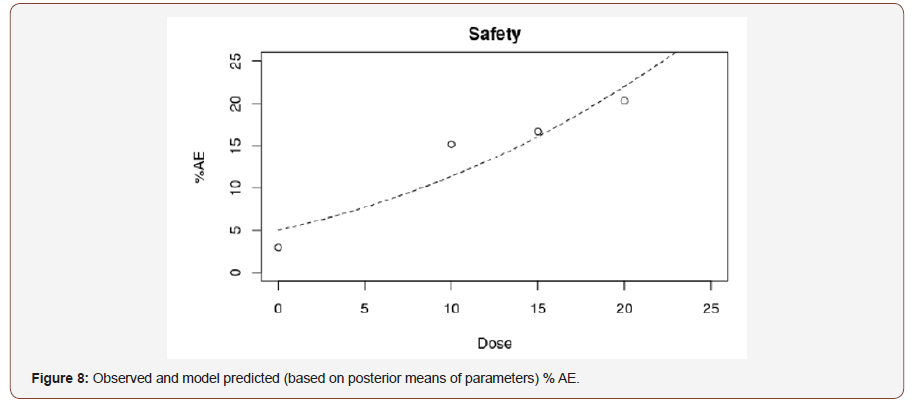
Concerning the definition of the utility function, in particular for the safety component, we decided to keep the exponent value k = 2, in order to put a quite high level of constraint on the required safety profile. Still on the safety component, the threshold to consider, s, is debatable: we propose to use the threshold s = 0.15, like in the simulation, as we consider that it is quite a high rate of discontinuation for AE. However for sensitivity analysis, we also assessed the decision performance when s was set to 0.10 and 0.20. For the application of the decision rule (Decision rule 1) the efficacy and safety cut-off values that govern the Go/No Go decision must be defined: for the safety, we kept the value of threshold.safe2=0.50 whereas for efficacy, because the standard sample size of typical phase III study in type 2 diabetes is rather 500-600 patients than 1000 patients, we propose to be very demanding in required power for the Go/NoGo decision: therefore we have chosen threshold. eff2=0.90. The results of the application of the decision rules are the following: with s = 0.15, the decision is ’Go’ and the selected dose is the first dose=10 mg with a posterior mean PoS almost equal to 1 and a posterior probability to have an observed percentage of discontinuation due to AEs ≤ s = 0.15 approximately equal to 0.95. As already mentioned, we assessed the decisions under safety thresholds of 0.10 and 0.20: with s = 0.10 the decision is ’NoGo’ because the best dose is 10mg but the posterior probability to have an observed percentage of discontinuation due to AEs ≤ s = 0.15 is too small ( 0.27 ) even for this lowest dose, whereas for s = 0.20 the decision is ’Go’ but still the dose=10mg remains the best one.
Discussion and Conclusions
The objective of this paper was to propose specific statistical methodologies to analyze the dose-finding study data in order to inform the decision rules defined within the proposed decisionmaking framework.
We have proposed a sponsor’s decision rule based on the posterior probabilities of the doses to be the optimal one (Decision rule 1 or Decision rule 1*): the chosen dose being the one that maximizes this posterior probability; we think that such a rule better accounts for the uncertainty in the parameter values than criteria based on the ordering of numerical estimates of the utilities (like the posterior mean or median of the utilities for instance, as in Decision rules 2, 3 and 4). In addition, it is an intuitive and understandable rule, that can be used as the basis to define a stopping rule for the interim analysis (rule based on a lower bound of probability of the chosen dose to be the optimal one).
Regarding sponsor’s strategy to choose the optimal dose with Decision rule 1*, by applying efficacy/safety rules at both MCMC and study levels, the sponsor is more restrictive regarding the dose choices. When comparing results between putting efficacy/safety constraints at both MCMC and study levels (as done with Decision rule 1*), and putting efficacy/safety constraints at the study level only (i.e. at the Go / NoGo decision level) as with Decision rule 1, it seems more reasonable to keep this second approach (Decision rule 1). In fact, this approach is preferred not only because it showed slightly better results compared to Decision rule 1*, but also because thresholds are already arbitrarily predefined with Decision rule 1*, and it becomes harder to justify the choice of these thresholds values.
Regarding the impact of phase II sample size, we have seen that to go from 80% of the maximal utility to 90%, it is quite demanding in terms of sample size: we should almost double the number of patients, regardless of efficacy/safety profiles. If the dose choice is more difficult (when the safety of the high dose is not very good, i.e. bad safety profile), it is more demanding in terms of number of patients to make good choices. So globally, and as for classic phase II power calculation, each incremental probability to achieve the study goal is more and more expensive (in terms of sample size). But we would recommend, in this case, the smaller sample sizes, as they are sufficient to reach 80% of the maximal utility, whereas reaching 90% would require to double the sample size and probably is not worth the investment. Therefore, we would recommend for instance 350 patients for phase II (rather than 700 patients) for the Sigmoid scenario combined with a bad safety profile. We think that this new approach is more consistent with the true objective of the phase II study (recommending a safe and active dose for phase III study).
On the other hand, we conclude that the two domination criteria
proposed for the interim analysis addressed in this paper do
not bring significant improvement compared to the first stopping
criterion, 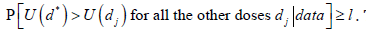
Acknowledgement
We would like to thank Mr. Loic Darchy, Mr. Pierre Colin and all the reviewers for their helpful comments and suggestions that led to an improved paper.
Conflict of Interest
The authors have declared no conflict of interest.
References
- Kirchner M, Kieser M, Gotte H, Schuler A (2016) Utility-based optimization of phase II/III programs. Statistics in Medicine 35(2): 305-316.
- Temple J (2012) Adaptive designs for Dose-finding trials. University of Bath, Department of Mathematical Sciences, pp. 1-206.
- Antonijevic Z, Kimber M, Manner D, Burman CF, Pinheiro J, et al. (2013) Optimizing Drug Development Programs: Type 2 Diabetes Case Study. Ther Innov Regul Sci 47(3): 363-374.
- Patel N, Bolognese J, Chuang-Stein C, Hewitt D, Gammaitoni A, et al. (2012) Designing phase II trials based on program-level considerations: a case study for neuropathic pain. Drug Information Journal 46(4): 439-454.
- Patel NR, Ankolekar S, Antonijevic Z, Rajicic N (2013) A mathematical model for maximizing the value of phase III drug development portfolios incorporating budget constraints and risk. Statistics in Medicine 32(10): 1763-1777.
- Foo LK, Duffull S (2017) Designs to balance cost and success rate for an early phase clinical study. Journal of Biopharmaceutical Statistics 27(1): 148-158.
- Antonijevic Z, Pinheiro J, Fardipour P, Lewis RJ (2010) Impact of Dose Selection Strategies Used in Phase II on the Probability of Success in Phase III. Statistics in Biopharmaceutical Research 2(4): 469-486.
- Gajewski BJ, Berry SM, Quintana M, Pasnoor M, Dimachkie M, et al. (2015) Building efficient comparative effectiveness trials through adaptive designs, utility functions, and accrual rate optimization: finding the sweet spot. Statistics in medicine 34(7): 1134-1149.
- Pinheiro J, Bornkamp B, Glimm E, Bretz F (2014) Model-based dose finding under model uncertainty using general parametric models. Statistics in Medicine 33(10): 1646-1661.
- Comets E (2010) Etude de la r´eponse aux m´edicaments par la mo elisation des relations dose-concentrationeffet. HAL. M´ Universit´e Paris-Diderot - Paris VII (tel-00482970): 1-84.
- Miller F, Guilbaud O, Dette H (2007) Optimal Designs for Estimating the Interesting Part of a Dose-Effect Curve. Journal of Biopharmaceutical Statistics 17(6): 1097-1115.
- Geweke J (2005) Contemporary Bayesian Econometrics and Statistics. Wiley, ISBN: 9780471679325.
- Savage LJ (1954) The Foundations of Statistics. Dover publications, USA, INC, (ISBN-13: 978-0486623498).
- Ravenzwaaij DV, Cassey P, Brown SD (2018) A simple introduction to Markov Chain Monte–Carlo sampling. Psychonomic Bulletin and Review 25(1): 143-154.
- Geyer CJ, Robert C, Casella G, Fan Y, Sisson SA, et al. (2011) Handbook of Markov Chain Monte Carlo. Chapman Hall/CRC, (ISBN: 9781420079425): 3-592.
- Chuang-Stein C (2006) Sample size and the probability of a successful trial. Pharmaceutical Statistics 5: 305-309.
- Christen JA, Muller P, Wathen K, Wolf J (2004) A Bayesian Randomized Clinical Trial: A Decision Theoretic Sequential Design. Canadian Journal of Statistics 32(4): 387-402.
-
Jihane Aouni, Jean Noel Bacro, Gwladys Toulemonde, Bernard Sebastien. Utility-Based Dose-Finding in Practice: Some Empirical Contributions and Recommendations. Annal Biostat & Biomed Appli. 3(1): 2019. ABBA.MS.ID.000552.
Trigonometric functions; Statistical distributions; Breast cancer; Odds T-X Contents
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






