 Opinion
Opinion
The New Size-Biased Kumaraswamy-G Distribution
Clement Boateng Ampadu, Department of Biostatistics, 31 Carrolton Road, Boston, MA 02132-6303, USA.
Received Date: September 17, 2019; Published Date: September 23, 2019
Abstract
This paper introduces a new size-biased distribution which is partially inspired by [1]. A member of this new class of distributions is shown to be practically significant in modeling real life data. Finally, we ask the reader to investigate further properties and applications of this new class of distributions.
Keywords: Size biased distribution; Regularized beta function; Normal distribution
The Size-Biased Kumaraswamy Distribution
The concept of weighted distributions is largely credited to
Fisher [1,2] and Rao [3]. In the size biased schemes, the probability
of sampling an individual is proportional to Xr provided that
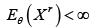 for all θ. In such situations, the weighted probability density function is defined as
for all θ. In such situations, the weighted probability density function is defined as
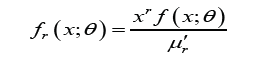
where When the probability of observing a positive-valued random variable is proportional to the value of the variable the resulting distribution is termed size-biased with probability density function
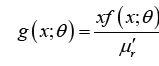
The Kumaraswamy distribution [4] has probability density function
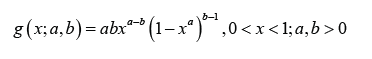
and the rth order raw moment is given by [1]
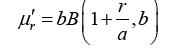
where 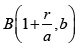 is a beta function defined by the integral
is a beta function defined by the integral
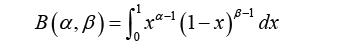
Notation 1.1. We write X SBKD(a,b) , if X is a size biased Kumaraswamy random variable
Proposition 1.2. [1] The PDF of the SBKD(a, b) distribution is given by

where 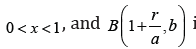 is a beta function defined by the
integral
is a beta function defined by the
integral
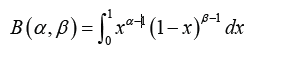
with a, b > 0
Theorem 1.3. [1] The CDF of the SBKD (a, b) distribution is given by
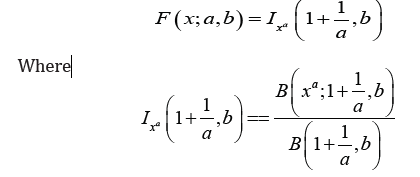
is the regularized incomplete beta function and is defined as the ratio of an incomplete beta function,
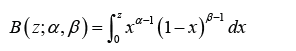
and the complete beta function,
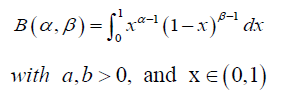
The 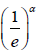
Definition 2.1. 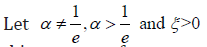 [5] Let where α is the
rate scale parameter and is a vector of parameters in the baseline
distribution all of whose entries are positive.
[5] Let where α is the
rate scale parameter and is a vector of parameters in the baseline
distribution all of whose entries are positive.
A random variable Z is said to follow the 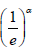
power transform family of distributions if the Cumulative Distribution Function (CDF) is given by
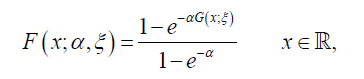
where the baseline distribution has CDF G(x;ξ ).
Proposition 2.2. [5] The PDF of the 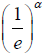 Proposition 2.2. [5] The PDF of the
Proposition 2.2. [5] The PDF of the
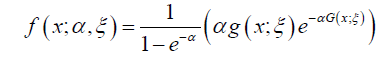
where 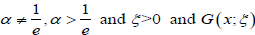 is the baseline
cumulative distribution with
is the baseline
cumulative distribution with
probability density function g (x;ξ )
The New Distribution
By modifying the parameter space for α in the 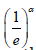 PT-Standard
Uniform family and using it in Theorem 1.3, we have the following
PT-Standard
Uniform family and using it in Theorem 1.3, we have the following
Proposition 3.1. The CDF of the new size biased Kumaraswamy Distribution is given by
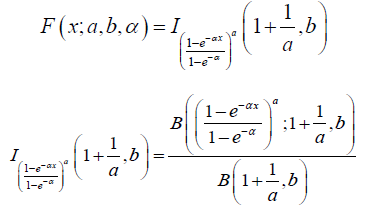
is the regularized incomplete beta function and is defined as the ratio of an incomplete beta function,
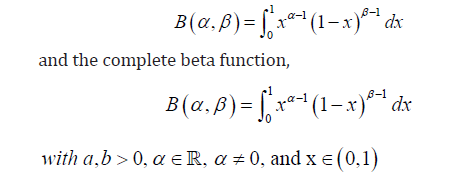
Using the above, we introduce the following
Definition 3.2. We say Z is a new size-biased Kumaraswamy-G random variable, and write SBKGD(a, b,α ,ξ ), if the CDF is given by
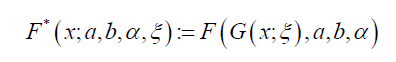
where F is given by the previous Proposition, a, b > 0, α ∈ R, α 6= 0, x ∈ R, and ξ is a vector of parameters in the baseline distribution with CDF G(x;ξ )
Remark 3.3. The PDF of the new size-biased Kumaraswamy-G family of distributions can be obtained by differentiating the CDF
Practical Illustration
We assume the baseline distribution is Normal with the following CDF
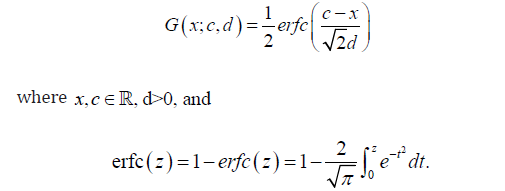
Thus from Definition 3.2 and Proposition 3.1, we have the following
Proposition 4.1. The CDF of the new size-biased Kumaraswamy- Normal distribution is given by
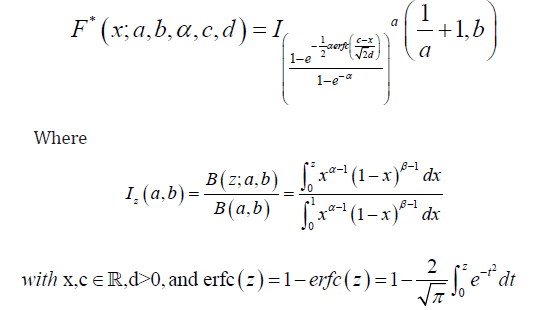
Remark 4.2. We write Q ∼ N SBKN D(a, b, α, c, d), if Q is a new size-biased Kumaraswamy-Normal random variable. When we fix a = 1, we denote the reduced distribution as N BIN D(b, α, c, d), and say Q is a new Beta-I-Normal random variable (Figure 1).
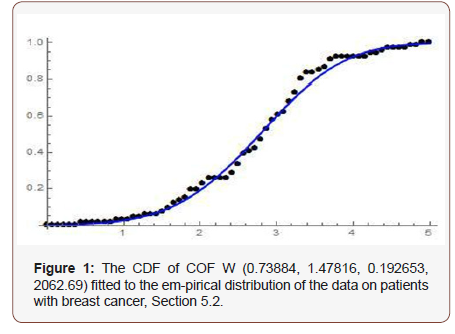
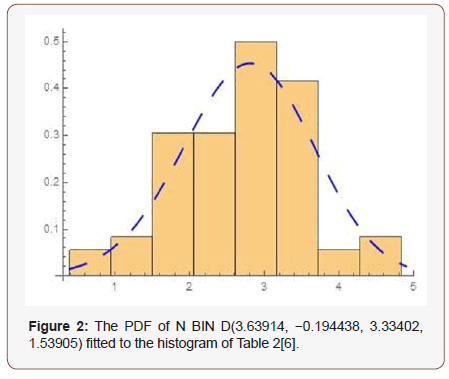
Remark 4.3. The PDF of the new size-biased Kumaraswamy- Normal distribution can be obtained by differentiating the CDF (Figure 2).
Conclusion
Size-biased distributions arise naturally in a range of sampling and modeling problems in forestry [7], as such we suggest to the reader to obtain some properties and applications of this new class of distributions as it pertains to forestry.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Dreamlee Sharma, Tapan Kumar Chakrabarty (2016) On Size Biased Kumaraswamy Distribution.
- Fisher RA (1934) The effects of methods of ascertainment upon the estimation of frequencies. Annals of Eugenics 6(1): 13-25.
- Rao CR (1965) On discrete distributions arising out of methods of ascertainment. In: Patil GP (Ed.), Classical and Contagious Discrete Distributions. Pergamon Press and Statistical Publishing Society: Calcutta, pp. 320-332
- Kumaraswamy PA (1980) Generalized probability density function for double-bounded ran-dom processes. Journal of Hydrology 46(1): 79-88.
- Abdulzeid Yen Anafo (2019) The New Alpha Power Transform: Properties and Ap-plications, Master of Science in Mathematical Sciences Essay, African Institute for Mathematical Sciences (Ghana). Unpublished Manuscript
- Ayman Alzaatreh, Carl Lee, Felix Famoye (2014) T-normal family of distributions: a new approach to generalize the normal distribution, Journal of Statistical Distributions and Applications 1: 16.
- Gove JH (2003) Estimation and applications of size-biased distributions in forestry. In: Amaro A, Reed D, Soares P (Eds.), Modeling Forest Systems; CABI Publishing, pp. 201-212.
-
Clement Boateng Ampadu. The New Size-Biased Kumaraswamy-G Distribution. Annal Biostat & Biomed Appli. 3(2): 2019. ABBA. MS.ID.000557.
Size biased distribution; Regularized beta function; Normal distribution
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






